Generative Adversarial Nets[Pre-WGAN]

---

本文来自《towards principled methods for training generative adversarial networks》，时间线为2017年1月，第一作者为WGAN的作者，Martin Arjovsky。
下面引用自令人拍案叫绝的Wasserstein GAN

要知道自从2014年Ian Goodfellow提出以来，GAN就存在着训练困难、生成器和判别器的loss无法指示训练进程、生成样本缺乏多样性等问题。从那时起，很多论文都在尝试解决，但是效果不尽人意，比如最有名的一个改进DCGAN依靠的是对判别器和生成器的架构进行实验枚举，最终找到一组比较好的网络架构设置，但是实际上是治标不治本，没有彻底解决问题。而今天的主角Wasserstein GAN（下面简称WGAN）成功地做到了以下爆炸性的几点：

• 彻底解决GAN训练不稳定的问题，不再需要小心平衡生成器和判别器的训练程度
• 基本解决了collapse mode的问题，确保了生成样本的多样性
• 训练过程中终于有一个像交叉熵、准确率这样的数值来指示训练的进程，这个数值越小代表GAN训练得越好，代表生成器产生的图像质量越高

以上一切好处不需要精心设计的网络架构，最简单的多层全连接网络就可以做到。那以上好处来自哪里？这就是令人拍案叫绝的部分了——实际上作者整整花了两篇论文，在第一篇《Towards Principled Methods for Training Generative Adversarial Networks》里面推了一堆公式定理，从理论上分析了原始GAN的问题所在，从而针对性地给出了改进要点；在第二篇《Wasserstein GAN》里面，又再从这个改进点出发推了一堆公式定理，最终给出了改进的算法实现流程，而改进后相比原始GAN的算法实现流程却只改了四点：

• 判别器最后一层去掉sigmoid
• 生成器和判别器的loss不取log
• 每次更新判别器的参数之后把它们的绝对值截断到不超过一个固定常数c
• 不要用基于动量的优化算法（包括momentum和Adam），推荐RMSProp，SGD也行

1 引言

GAN近些年变成了学术界的宠儿，其应用在诸多领域上，然而其还是明显受到难以训练的困扰，虽然大家都想解决该问题，不过目前为止，却没有理论的分析GAN训练的不稳定性原因。而且解决该问题的方法还是依赖启发式，而其对修改及其敏感，这限制了他们的应用。
本文作者发现GAN的生成器和其他VAE并没有明显差别，都是首先从一个简单先验进行采样\(z\sim p(z)\),然后输出最后的采样\(g_{\theta}(z)\)，有时候会在最后加上噪音。总之，\(g_{\theta}\)是一个受到参数\(\theta\)控制的神经网络，主要的差别就是\(g_{\theta}\)是如何训练的。

之前认为生成模型依赖最大似然，或者等效于最小化未知的真实数据分布\(\mathbb{P}_r\)和生成器分布\(\mathbb{P}_g\)（依赖于\(\theta\)）之间的KL散度。如果假设这两个分布都是连续密度\(P_r\)和\(P_g\)，那么这些方法就是最小化：

\[\begin{align}KL(\mathbb{P}_r||\mathbb{P}_g)=\int_x P_r(x)\log \frac{P_r(x)}{P_g(x)}dx\end{align} \]

这个损失函数有很好的特性，其有唯一最小值，当且仅当\(\mathbb{P}_r = \mathbb{P}_g\)，而且优化时，不需要事先知道\(P_r(x)\)的相关信息，只需要采样。然而当\(\mathbb{P}_r\)和\(\mathbb{P}_g\)之间不是对称的时候就有趣了：

• 如果\(P_r(x)>P_g(x)\)，那么\(x\)是一个数据点，其来自真实数据的概率要远大于生成的。该现象的本质通常被描述为“mode dropping”：当很大区域是\(P_r\)的高值，而\(P_g\)是很小或者零值。当\(P_r(x)>0\)但是\(P_g(x)\rightarrow 0\)时，KL内部的被积函数迅速增长到无穷大，这意味着这个损失函数赋予生成器的分布（那些没有覆盖到数据的部分）极大的cost值。
• 如果\(P_r(x)<P_g(x)\)，那么\(x\)表示来自生成的概率远大于真实数据的。这种情况下我们可以看到生成器的输出基本看上去很假。当\(P_r(x) \rightarrow 0\)且\(P_g(x)>0\)时，发现KL中的值接近为0，意味着损失函数会将极低的值给生成器（此时生成的数据看上去很假）。

很明显，如果最小化\(KL(\mathbb{P}_g||\mathbb{P}_r)\)，损失函数的权重就会反过来，即损失函数会在生成很假样本的时候给予很高的cost值。GAN是优化（最原始形态）jensen-shannon散度(Jensen-shannon divergence, JSD)，这两个cost的转换形式为：

\[\begin{align}JSD(\mathbb{P}_r||\mathbb{P}_g)=\frac{1}{2}KL(\mathbb{P}_r||\mathbb{P}_A)+\frac{1}{2}KL(\mathbb{P}_g||\mathbb{P}_A) \end{align} \]

这里\(\mathbb{P}_A\)是平均分布，密度为\(\frac{P_r+P_g}{2}\)。文献[13]中就做了关于他们相似性的实验性分析。的确有人猜测，GAN成功生成看似真实图像的原因是由于传统的最大似然方法的转换。然而该问题并未结束。

GAN形式化成2个步骤，首先训练一个判别器D去最大化：

\[\begin{align}L(D,g_{\theta})=\mathbb{E}_{x\sim \mathbb{P}_r}\left[ \log D(x)\right]+\mathbb{E}_{x\sim \mathbb{P}_g}\left[ \log(1-D(x))\right] \end{align} \]

可以发现最优判别器形如：

\[\begin{align} D^*(x)=\frac{P_r(x)}{P_r(x)+P_g(x)} \end{align} \]

上述推论过程：

• 当固定生成器G，此时训练判别器，其lost函数为式子5：

\[\begin{align}lost = P_r \log D(x)+ P_g \log(1-D(x)) \end{align} \]

将其关于\(D(x)\)进行求导：

\[\begin{align}\frac{P_r}{ D(x)}-\frac{ P_g }{1-D(x)} \end{align} \]

将其等于0，得,即为式子7：

\[\begin{align}D^*(x)=\frac{P_r(x)}{P_r(x)+P_g(x)} \end{align} \]

则反向带入，此时式子7为：

\[\begin{align}\mathbb{E}_{x\sim \mathbb{P}_r}\left[ \log \frac{P_r(x)}{P_r(x)+P_g(x)} \right]+\mathbb{E}_{x\sim \mathbb{P}_g}\left[ \log \frac{P_g(x)}{P_r(x)+P_g(x)} \right] \end{align} \]

而当最优判别器，就是对真实值的预测等于生成的，对半分别为0.5，则此时式子1等于\(\log\frac{1}{2}+\log\frac{1}{2}=-\log4=-2\log2\)
此时最优\(L(D,g_{\theta})\)等于：
\(\begin{align}L(D,g_{\theta})=(-2\log2)+(2\log2)+(lost) \end{align}\)
将后面2项合并：

\[\begin{align}-2\log2+\left(\log2+\mathbb{E}_{x\sim \mathbb{P}_r}\left[ \log D(x)\right]\right) + \left(\log2+\mathbb{E}_{x\sim \mathbb{P}_g}\left[ \log(1-D(x))\right] \right) \end{align} \]

进一步：

\[\begin{align} -2\log2+ P_r \log\frac{P_r}{\frac{1}{2}(P_r+P_g)}+ P_g \log\frac{P_g}{\frac{1}{2}(P_r+P_g)} \\ -2\log2+KL\left(P_r||\frac{P_r+P_g}{2}\right)+KL\left(P_g||\frac{P_r+P_g}{2}\right) \end{align}\]

进而得到：

\[\begin{align}-2\log2+2\cdot JSD(P_r||P_g) \end{align} \]

从而结果得到\(L(D^*,g_{\theta})=2JSD(\mathbb{P}_r||\mathbb{P}_g)-2\log2\)，因此，当鉴别器是最优的时，最小化等式（2）看成最小化Jensen-Shannon散度的\(\theta\)的函数。所以理论上，我们期望首先尽可能最优的训练判别器（所以\(\theta\)时候的cost函数近似JSD），然后在\(\theta\)上进行梯度迭代，然后交替这2个事情。然而，这并不work。判别器目标函数越小，则实际上就是\(P_r\)和\(P_g\)之间的JS散度越小，通过优化JS散度就能将\(P_g\)“拉向”\(P_r\)，最终以假乱真。实际上，判别器越好，对生成器的更新就会越糟糕，原始GAN论文认为这个问题主要来自饱和，换成另一个相似cost函数就不会有这个问题了。然而即使使用新的cost函数，更新还是会变得更糟，优化也会变得更不稳定。
因此，就有下面几个问题：

• 为什么判别器变得越来越好，而更新却越来越差？在原始cost函数和新的cost函数都是这样；
• 为什么GAN训练这么不稳定；
• 是否新的cost函数和JSD是一样的相似散度？如果是，他的特性是什么？；
• 有方法避免这些问题么？

2 不稳定的来源

理论上训练的判别器的cost基本就是\(2\log2-2JSD(\mathbb{P}_r||\mathbb{P}_g)\)。然而实际上，如果只训练D直到收敛，他的误差接近0。

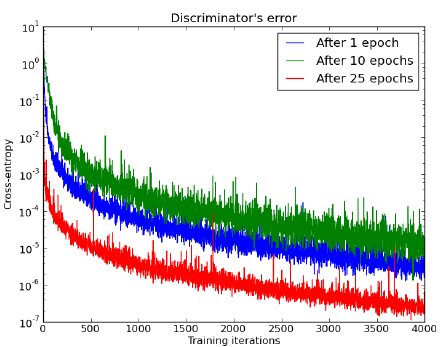
如图1,可以发现基于他们的JSD已经有一个完全胜出了，并不是均衡。这种情况发生的时候是要么分布是非连续的，或者他们的支撑集（supports）不相交。

这里介绍几个概念术语,来自这里

• 支撑集（support）其实就是函数的非零部分子集，比如ReLU函数的支撑集就是(0, +\(\infty\))，一个概率分布的支撑集就是所有概率密度非零部分的集合。
• 流形（manifold）是高维空间中曲线、曲面概念的拓广，我们可以在低维上直观理解这个概念，比如我们说三维空间中的一个曲面是一个二维流形，因为它的本质维度（intrinsic dimension）只有2，一个点在这个二维流形上移动只有两个方向的自由度。同理，三维空间或者二维空间中的一条曲线都是一个一维流形。
• 测度（measure）是高维空间中长度、面积、体积概念的拓广，可以理解为“超体积”

一个导致分布非连续的原因是，是否他们的支撑集（supports）位于低维度流行上。文献[10]中证明\(\mathbb{P}_r\)确实非常集中在低维流形上[10]。

在GAN中，\(\mathbb{P}_g\)的定义是从一个简单先验\(z\sim p(z)\)进行采样，然后应用一个函数\(g:\mathcal{Z}\rightarrow \mathcal{X}\)，所以\(\mathbb{P}_g\)的支撑集被包含在\(g(\mathcal{Z})\)里面。如果\(\mathcal{Z}\)的维度小于\(\mathcal{X}\)的维度（通常都是这样，采样128维，然后生成28x28的图片），那么是不可能让\(\mathbb{P}_g\)变成连续的 。这是因为在大多数情况下\(g(\mathcal{Z})\)会被包含在一个低维度流行的联合体上，因此在\(\mathcal{X}\)中有测度0存在。而直观上，这是高度非平凡的，因为一个\(n\)维的参数绝对不会意味着图片会处于\(n\)维流行上。事实上，有许多简单的反例，如Peano曲线，lemniscates等等。

下面是对应白话文,来自这里

• 如果两个分布完全没有重叠的部分，或者它们重叠的部分可忽略（下面解释什么叫可忽略），它们的JS散度是多少呢？
  答案是\(\log 2\)，因为对于任意一个\(x\)只有四种可能：
  \(P_1(x) = 0\)且\(P_2(x) = 0\)
  \(P_1(x) \neq 0\)且\(P_2(x) \neq 0\)
  \(P_1(x) = 0\)且\(P_2(x) \neq 0\)
  \(P_1(x) \neq 0\)且\(P_2(x) = 0\)
  第一种对计算JS散度无贡献，第二种情况由于重叠部分可忽略所以贡献也为0，第三种情况对公式0右边第一个项的贡献是\(\log \frac{P_2}{\frac{1}{2}(P_2 + 0)} = \log 2\)，第四种情况与之类似，所以最终\(JS(P_1||P_2) = \log 2\)。换句话说，无论\(P_r\)跟\(P_g\)是远在天边，还是近在眼前，只要它们俩没有一点重叠或者重叠部分可忽略，JS散度就固定是常数\(\log 2\)，而这对于梯度下降方法意味着——梯度为0！此时对于最优判别器来说，生成器肯定是得不到一丁点梯度信息的；即使对于接近最优的判别器来说，生成器也有很大机会面临梯度消失的问题。但是\(P_r\)与\(P_g\)不重叠或重叠部分可忽略的可能性有多大？不严谨的答案是：非常大。比较严谨的答案是：当\(P_r\)与\(P_g\)的支撑集是高维空间中的低维流形时，\(P_r\)与\(P_g\)重叠部分测度为0的概率为1。

• 当\(P_r\)与\(P_g\)的支撑集是高维空间中的低维流形时，这句话基本上是成立的。原因是GAN中的生成器一般是从某个低维（比如100维）的随机分布中采样出一个编码向量，再经过一个神经网络生成出一个高维样本（比如64x64的图片就有4096维）。当生成器的参数固定时，生成样本的概率分布虽然是定义在4096维的空间上，但它本身所有可能产生的变化已经被那个100维的随机分布限定了，其本质维度就是100，再考虑到神经网络带来的映射降维，最终可能比100还小，所以生成样本分布的支撑集就在4096维空间中构成一个最多100维的低维流形，“撑不满”整个高维空间。

• “撑不满”就会导致真实分布与生成分布难以“碰到面”，这很容易在二维空间中理解：一方面，二维平面中随机取两条曲线，它们之间刚好存在重叠线段的概率为0；另一方面，虽然它们很大可能会存在交叉点，但是相比于两条曲线而言，交叉点比曲线低一个维度，长度（测度）为0，可忽略。三维空间中也是类似的，随机取两个曲面，它们之间最多就是比较有可能存在交叉线，但是交叉线比曲面低一个维度，面积（测度）是0，可忽略。从低维空间拓展到高维空间，就有了如下逻辑：因为一开始生成器随机初始化，所以\(P_g\)几乎不可能与\(P_r\)有什么关联，所以它们的支撑集之间的重叠部分要么不存在，要么就比\(P_r\)和\(P_g\)的最小维度还要低至少一个维度，故而测度为0。所谓“重叠部分测度为0”，就是上文所言“不重叠或者重叠部分可忽略”的意思。

• 我们就得到了本文中关于生成器梯度消失的第一个论证：在（近似）最优判别器下，最小化生成器的loss等价于最小化\(P_r\)与\(P_g\)之间的JS散度，而由于\(P_r\)与\(P_g\)几乎不可能有不可忽略的重叠，所以无论它们相距多远JS散度都是常数\(\log 2\)，最终导致生成器的梯度（近似）为0，梯度消失。

为了形式化说明这点，假设\(g\)是一个NN。下面给出引理：
引理1
令\(g:\mathcal(Z)\rightarrow \mathcal{X}\)是一个函数，其由仿射映射，逐点非线性（可以是ReLU，LReLU，或者就是严格平滑增加的函数如sigmoid，tanh，softplus等等）。然后\(g(\mathcal{Z})\)是包含在一个维度接近\(\mathcal{Z}\)的可数流行并集上（这里就有点测度论的”可数无穷个不相交的集合的测度之和等于其集合并集的测度“意思了。）。因此，如果\(\mathcal{Z}\)的维度小于\(\mathcal{X}\)，那么\(g(\mathcal{Z})\)会让\(\mathcal{X}\)中有许多测度为0的存在。
证明：略

如上结论，如果\(\mathbb{P}_r\)和\(\mathbb{P}_g\)的支撑集是不相交或者位于低维流行上，那么总是存在一个完美的判别器。接下来介绍这是怎么发生的，而且为什么会导致生成器训练不稳定。

2.1 完美的判别理论

为了简洁，首先解释下什么时候\(\mathbb{P}_r\)和\(\mathbb{P}_g\)会存在不相交支撑集（disjoint supports）。我们说一个判别器\(D:\mathcal{X}\rightarrow [0,1]\)的准确值为1时，即此时判别器在包含\(\mathbb{P}_r\)的支撑集上判定其为1，而在包含\(\mathbb{P}_g\)的支撑集上判定其为0.即\(\mathbb{P}_r[D(x)=1]=1\)和\(\mathbb{P}_g[D(x)=0]=1\)。

理论2.1
如果两个分布\(\mathbb{P}_r\)和\(\mathbb{P}_g\)的支撑集分别包含在两个不相交且紧凑的集合\(\mathcal{M}\)和\(\mathcal{P}\)，那么存在一个平滑最优的判别器\(D^*:\mathcal{X}\rightarrow [0,1]\)，其准确值为1（即此时一定存在一个判别器能够完全划分这两个集合），且此时对于所有的\(x\in\mathcal{M}\cup\mathcal{P}\)有\(\bigtriangledown_x D^*(x)=0\)
证明
判别器是训练并且最大化

\[\mathbb{E}_{x\sim\mathbb{P}_r}[\log D(x)]+\mathbb{E}_{x\sim\mathbb{P}_g}[\log(1-D(x))] \]

因为\(\mathcal{M}\)和\(\mathcal{P}\)都是紧凑且不相关的，那么z这两个集合之间的距离存在\(0<\delta =d(\mathcal{P},\mathcal{M})\)。现在定义：

\[\begin{align} \hat{\mathcal{M}} = \{ x:d(x,M) \leq \frac{\delta}{3} \} \\ \hat{\mathcal{P}}= \{x:d(x,P)\leq \frac{\delta}{3}\} \end{align}\]

通过\(\delta\)的定义，\(\hat{\mathcal{M}}\)和\(\hat{\mathcal{P}}\)清晰的是两个不相关紧凑集合。因此，通过Urysohn的平滑理论，会存在一个平滑函数\(D^*:\mathcal{X}\rightarrow [0,1]\),使得\(D^*|_{\hat{\mathcal{M}}}\equiv 1\)和\(D^*|_{\hat{\mathcal{P}}}\equiv 0\)。因为对于所有的位于\(\mathcal{P}_r\)的支撑集中的变量\(x\)，都有\(\log D^*(x)=0\)，而对于所有位于\(\mathcal{P}_g\)的支撑集中的变量\(x\)，都有\(\log (1-D^*(x))=1\)，判别器是完全最优且准确值为1。令\(x\)位于\(\mathcal{M}\cup \mathcal{P}\)。假设\(x\in\mathcal{M}\)，存在一个开区间球\(B=B(x,\frac{\delta}{3})\)，且\(D^*|_{B}\)是一个常量。此时\(\triangledown_xD^*(x) \equiv 0\)，即梯度就是为0，如果\(x\in\mathcal{P}\)那么结果也是一样。得证。

在下一个理论中，先放弃不相交的假设，将其推广到更一般的情况，假设是2个不同的流行。然而，如果这两个流行在很大部分空间上都是完美匹配的，那么意味着没有判别器可以将它们进行区分。直观上，具有这种情况的两个低维度流行还是很少存在的：对于在特定段中空间匹配的两条曲线，它们不能以遭受任何任意的小方式扰动下还能满足该属性。（即在低维流行中进行稍微扰动下，就分开了）。为此，我们将定义两个流形完美对齐的概念，并表明在任意的小扰动下，该属性永远不会以概率1保持。（即一扰动，该属性就会被破坏）.

定义2.1
令\(\mathcal{M}\)和\(\mathcal{P}\)是两个关于\(\mathcal{F}\)的无边界常规子流行，这里简单认为\(\mathcal{F}=\mathbb[R]^d\)。\(x\in \mathcal{M}\cap\mathcal{P}\)是这两个流行的交叉点。如果有\(\mathcal{T}_x\mathcal{M}+\mathcal{T}_x\mathcal{P}=\mathcal{T}_x\mathcal{F}\)，我们就说\(\mathcal{M}\)和\(\mathcal{P}\)在\(x\)上横向交叉，这里\(\mathcal{T}_x\mathcal{M}\)表示\(\mathcal{M}\)上围绕\(x\)的切线空间。

定义2.2
我们说两个没有边界的流行\(\mathcal{M}\)和\(\mathcal{P}\)是完美对齐是，如果有\(x\in \mathcal{M}\cap\mathcal{P}\)，那么\(\mathcal{M}\)和\(\mathcal{P}\)不在\(x\)上横向交叉。
这里将流行\(M\)的边界表示为\(\partial M\)，内部表示为\(Int M\)。我们说两个流行\(\mathcal{M}\)和\(\mathcal{P}\)（不管是否有边界）完美对齐是基于下面四组中（\(Int \mathcal{M}\), \(Int \mathcal{P}\)）,（\(Int \mathcal{M}\),\(\partial \mathcal{P}\)），（\(\partial \mathcal{M}\), \(Int \mathcal{P}\)），（\(\partial \mathcal{M}\),\(\partial \mathcal{P}\)）任意一组无边界流行对完全对齐成立前提下。

有趣的是，在实际中，我们可以很安全的假设任意两个流行不是完美对齐的，因为在这两个流行上任意一个小的扰动都会导致他们有横向交叉或者甚至不交叉。这可以通过引理2进行叙述和证明。

如引理3所述，如果两个流行不完美对齐，那么他们的交集\(\mathcal{L}=\mathcal{M}\cap\mathcal{P}\)是一个有限流行的并集，其中维度严格小于\(\mathcal{M}\)和\(\mathcal{P}\)。

引理2
令\(\mathcal{M}\)和\(\mathcal{P}\)是\(\mathbb{R}^d\)的两个常规子流行，且没有所有的维度。同时令\(\eta\),\(\eta^{'}\)是任意独立的连续随机变量。因此定义扰动的流行为\(\tilde{\mathcal{M}}=\mathcal{M}+\eta\)和\(\tilde{\mathcal{P}}=\mathcal{P}+\eta^{'}\)，那么：

\[\mathbb{P}_{\eta,\eta^{'}}(\tilde{\mathcal{M}}与\tilde{\mathcal{P}}不是完美对齐)=1 \]

引理3
令\(\mathcal{M}\)和\(\mathcal{P}\)是\(\mathbb{R}^d\)的两个常规子流行，他们不是完美对齐且没有所有维度。令\(\mathcal{L}=\mathcal{M}\cap\mathcal{P}\)。如果\(\mathcal{M}\)和\(\mathcal{P}\)没有边界，那么\(\mathcal{L}\)同样也是一个流行，并且维度严格低于\(\mathcal{M}\)和\(\mathcal{P}\)。如果他们有边界，那么\(\mathcal{L}\)是一个最多4个（可数的）严格更低维度流行的并集。在这两种情况中，\(\mathcal{L}\)在\(\mathcal{M}\)和\(\mathcal{P}\)上的测度为0.

现在叙述下在这种情况下，基于两个流行上最优判别器结果。

定理2.2
令\(\mathbb{P}_r\)和\(\mathbb{P}_g\)是两个分布，其支撑集包含在两个封闭的流行\(\mathcal{M}\)和\(\mathcal{P}\)上，这两个流行没有完美对齐，且没有所有维度。并假设\(\mathbb{P}_r\)和\(\mathbb{P}_g\)在他们各自流行内是连续的，意味着如果有一个集合\(A\)，其在\(\mathcal{M}\)上的测度为0，那么\(\mathbb{P}_r(A)=0\)（对于\(\mathbb{P}_g\)也是一样）。然后，存在一个最优判别器\(D^*:\mathcal{X}\rightarrow [0,1]\)的准确度为1，且对于几乎任意\(\mathcal{M}\)和\(\mathcal{P}\)中的变量\(x\)，\(D^*\)在\(x\)周边是平滑的，且\(\bigtriangledown_x D^*(x)=0\)。

这两个定理告诉我们存在一个最优判别器，其在\(\mathbb{P}_r\)和\(\mathbb{P}_g\)几乎任何地方都是平滑而且是常量。所以事实就是该判别器在流行点上是常量，所以没法通过BP学到任何信息，同时在下面介绍的也是常量。下面的定理2.3是将整个理论进行总结得出的。
定理2.3
令\(\mathbb{P}_r\)和\(\mathbb{P}_g\)是两个分布，其支撑集包含在两个封闭的流行\(\mathcal{M}\)和\(\mathcal{P}\)上，这两个流行没有完美对齐，且没有所有维度。并假设\(\mathbb{P}_r\)和\(\mathbb{P}_g\)在他们各自流行内是连续的，那么：

\[\begin{align} JSD(\mathbb{P}_r||\mathbb{P}_g) =\log2 \\ KL(\mathbb{P}_r||\mathbb{P}_g) = +\infty \\ KL(\mathbb{P}_g||\mathbb{P}_r) = +\infty \end{align}\]

注意到即使两个流行彼此靠得很近，这些散度也会maxed out。而就算生成器生成的样本看上去很好，可是此时两个KL散度可能很大。因此，定理2.3指出使用那些通常用来测试两个分布之间相似性的方法并不是一个好主意。更不用说，如果这些散度总是maxed out并试图通过梯度下降进行最小化也是不可能的。我们期望有一个softer的测度，可以包含流行中点之间距离的概念。

下面白话结论来自这里

• 有了这些理论分析，原始GAN不稳定的原因就彻底清楚了：判别器训练得太好，生成器梯度消失，生成器loss降不下去；判别器训练得不好，生成器梯度不准，四处乱跑。只有判别器训练得不好不坏才行，但是这个火候又很难把握，甚至在同一轮训练的前后不同阶段这个火候都可能不一样，所以GAN才那么难训练。

2.2 每个cost函数的结果和问题

定理2.1和定理2.2得出一个很重要的事实。如果我们关心的两个分布的支撑集是不相关或者位于低维流行上的，最优判别器可能是完美的，而且梯度几乎在任何地方都是0.

2.2.1 原始的cost函数

接下来将介绍下当通过一个判别器将梯度传递给生成器时会发生什么。与目前为止的典型分析一个关键区别是，作者将开发一套理论来近似最优判别器，而不是使用（未知）真正的判别器。并证明随着近似越来越好，所观察到的梯度消失或者大规模不稳定的行为主要依赖使用的cost函数。
将\(||D||\)表示范数：

\[\begin{align} ||D||=\underset{x\in\mathcal{X}}{sup}|D(x)|+||\bigtriangledown_x D(x)||_2\end{align} \]

该范数的使用可以让证明变得更简单，但是可以在另一个Sobolev范数中完成\(||\cdot||_{1,p}\),对于普遍逼近定理所涵盖的\(p<\infty\)，此时可以保证在这个范数中的神经网络近似[5]。

定理2.4（在生成器上的梯度消失）
令\(g_{\theta}:\mathcal{Z}\rightarrow \mathcal{X}\)是一个微分函数，表示分布一个分布\(\mathbb{P}_g\)。令\(\mathbb{P}_r\)表示真实数据分布，D表示一个可微分的判别器。如果定理2.1和2.2都满足，\(||D-D^*||<\epsilon\)且\(\mathbb{E}_{z\sim p(z)}\left[ ||J_{\theta}g_{\theta}(z)||_2^2\right]\leq M^2\)（因为M依赖于\(\theta\),对于均匀分布先验和NN，该条件可以简单验证。而对于高斯先验需要更多的工作，因为我们需要限制\(z\)的增长，但是对当前结构同样适用。），那么：

\[\begin{align}||\bigtriangledown_{\theta}\mathbb{E}_{z\sim p(z)}\left[\log(1-D(g_{\theta}(z))\,\,)\right]||_2<M\frac{\epsilon}{1-\epsilon}\end{align} \]

证明。在定理2.1和定理2.2的证明中，\(D^*\)在\(\mathbb{P}_g\)的支撑集上局部为0.那么在该支撑集上使用Jensen不等式和链式法则，得：

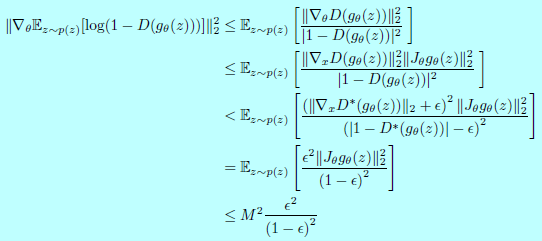
将其开方得：

\[\begin{align}||\bigtriangledown_{\theta}\mathbb{E}_{z\sim p(z)}\left[\log(1-D(g_{\theta}(z))\,\,)\right]||_2<M\frac{\epsilon}{1-\epsilon}\end{align} \]

得证。

推理 2.1
基于与定理2.4一样的假设：

\[\begin{align} \underset{||D-D^*||\rightarrow 0}{\lim} \bigtriangledown_{\theta}\mathbb{E}_{z\sim p(z)}\left[\log(1-D(g_{\theta}(z))\,\,)\right]=0 \end{align} \]

可以发现判别器训练的越好，则生成器梯度就会消失，为了完整，这里增加了对应的实验，如图2

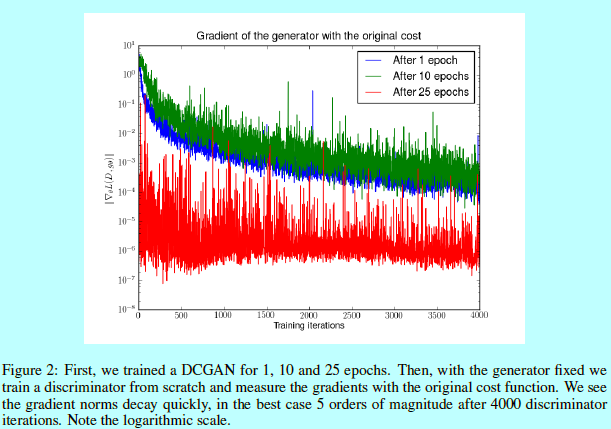
事实是，生成器的cost函数接近Jensen-Shannon散度取决于近似的质量好坏。这点告诉我们一个基础理论：要么判别器的更新是不准确的或者直接梯度会消失。这使得训练这个cost变得很困难或者需要用户来决定准确的判别器训练过程，从而让GAN训练变得很困难。

2.2.2 生成器的代替函数-log D（the -log D alternative）

为了避免判别器很好时候梯度消失的问题，人们选择使用一个不同的cost函数：

\[\begin{align} \Delta \theta=\bigtriangledown_{\theta}\mathbb{E}_{z\sim p(z)}[-\log D(g_{\theta}(z))] \end{align} \]

现在先叙述并证明该梯度优化的cost函数，随后，证明虽然该梯度不一定会受到消失梯度的影响，但它确实会在最优判别器的噪音近似下导致大量不稳定的更新（在实验中已经广泛证实）。

定理2.5
令\(\mathbb{P}_r\)和\(\mathbb{P}_{g \theta}\)表示2个连续分布，对应密度为\(P_r\)和\(P_{g \theta}\)。令\(D^*=\frac{P_r}{P_{g\theta_0}+P_r}\)是最优判别器，此时\(\theta_0\)是固定的（迭代生成器的时候，判别器是固定的）。那么：

\[\begin{align} \mathbb{E}_{z\sim p(z)}\left[ -\bigtriangledown_{\theta}\log D^*(g_{\theta}(z))|_{\theta=\theta_0}\right]=\bigtriangledown_{\theta}\left[ KL(\mathbb{P}_{g\theta}||\mathbb{P}_r)-2JSD(\mathbb{P}_{g\theta}||\mathbb{P}_r)\right] |_{\theta=\theta_0} \end{align} \]

关于式子24的推导过程，来自这里

• 原始生成器的loss为改成

\[\begin{align}\mathbb{E}_{x\sim P_g}[-\log D(x)]\end{align} \]

且在得到最优判别器下

\[\begin{align}\mathbb{E}_{x\sim P_r}[\log D^*(x)]+\mathbb{E}_{x\sim P_g}[\log(1- D^*(x))]=2JSD(P_r||P_g)-2\log 2\end{align} \]

将KL散度变换成最优判别器：

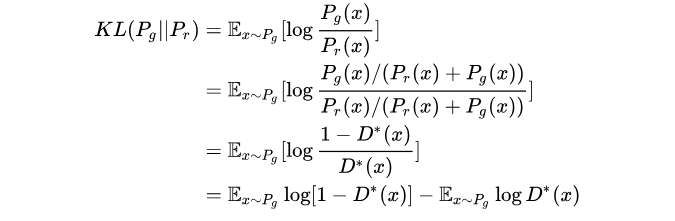
由上面三个式子得最小化目标的等价变形为：

上面式子最后两项不依赖生成器G，从而可以略去，最后得到：

\[KL(\mathbb{P}_{g\theta}||\mathbb{P}_r)-2JSD(\mathbb{P}_{g\theta}||\mathbb{P}_r) \]

可以从式子24和上述式子发现，是一个倒KL减去两个JSD，即最小化生成分布与真实分布的KL散度，却又要最大化两者的JSD散度，一个拉近，一个推远。第二，在\(KL(\mathbb{P}_{g\theta}||\mathbb{P}_r)\)中的KL不是一个最大似然的近似。而\(KL(\mathbb{P}_{g\theta}||\mathbb{P}_r)\)与\(KL(\mathbb{P}_r||\mathbb{P}_g)\)是不同的，正如我们所知，第一种KL会赋予生成看上去很假的样本很高的cost，在mode dropping时候赋予很低的cost；而JSD是对称的，所以他不应该改变这种行为。这就解释了实际中看到的，GAN（当稳定时候）创建看上去不错的样本，但是GAN遭受大规模mode dropping的影响。

如以\(KL(\mathbb{P}_{g\theta}||\mathbb{P}_r)\)为例：

• 当 \(P_g(x)\rightarrow 0\)而\(P_r(x)\rightarrow 0\)时，\(P_g(x)\log\frac{P_g(x)}{P_r(x)}\rightarrow 0\),对\(KL(\mathbb{P}_{g\theta}||\mathbb{P}_r)\)贡献趋近于0；
• 当 \(P_g(x)\rightarrow 1\)而\(P_r(x)\rightarrow 0\)时，\(P_g(x)\log\frac{P_g(x)}{P_r(x)}\rightarrow +\infty\),对\(KL(\mathbb{P}_{g\theta}||\mathbb{P}_r)\)贡献趋近于正无穷；

换言之，\(KL(\mathbb{P}_{g\theta}||\mathbb{P}_r)\)对于上面两种错误的惩罚是不一样的，第一种错误对应的是“生成器没能生成真实的样本”，惩罚微小；第二种错误对应的是“生成器生成了不真实的样本” ，惩罚巨大。第一种错误对应的是缺乏多样性，第二种错误对应的是缺乏准确性。这一放一打之下，生成器宁可多生成一些重复但是很“安全”的样本，也不愿意去生成多样性的样本，因为那样一不小心就会产生第二种错误，得不偿失。这种现象就是大家常说的collapse mode。

所以总结：在原始GAN的（近似）最优判别器下，第一种生成器loss面临梯度消失问题，第二种生成器loss(式子25)面临优化目标荒谬、梯度不稳定、对多样性与准确性惩罚不平衡导致mode collapse这几个问题。

定理2.6（生成器梯度更新的不稳定）
略

即使我们忽略了更新会有无限的变化（即方差很大），仍然认为更新的分布是可以中心化的，这意味着如果我们限定更新，更新的期望将为0，即不向梯度提供任何反馈。
因为关于\(D\)和\(bigtriangledown D\)的噪音是去相关的假设太严格了，如图3.

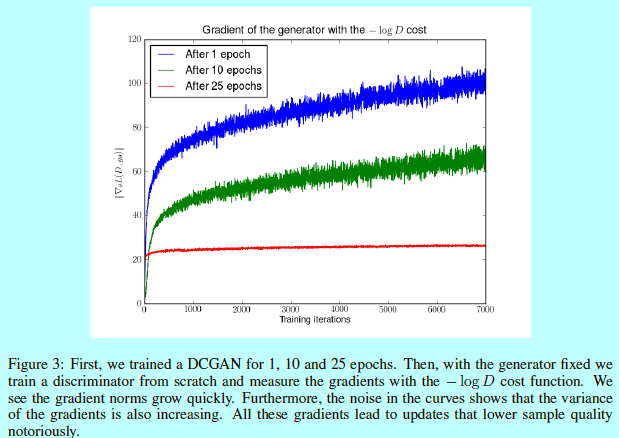
如图3，在训练稳定良好的DCGAN的任何阶段，除非已经收敛，否则当我们训练鉴别器接近最优时，梯度的范数会急剧增长。在所有情况下，使用此更新会导致样本质量不断下降。曲线中的噪音显示梯度的方差也在不断增长，而这会减缓收敛并且在优化阶段会有更多不稳定的行为[1]。

3 更柔和的指标和分布

一个很重要的问题是如何修复不稳定和梯度消失的问题。我们打破这些定理假设的一个方法就是给判别器输入增加连续噪音，因而平滑概率质量的分布。

定理3.1
如果\(X\)分布为\(\mathbb{P}_X\)，其支撑集为\(\mathcal{M}\),\(\epsilon\)是一个完全连续的随机变量，其密度为\(P_{\epsilon}\)，那么\(\mathbb{P}_{X+\epsilon}\)是完全连续的，其密度为：

\[\begin{align} P_{X+\epsilon}(x) &= \mathbb{E}_{y\sim \mathbb{P}_X}[P_{\epsilon}(x-y)] \\ &= \int_{\mathcal{M}}P_{\epsilon}(x-y)d\mathbb{P}_X(y) \end{align}\]

推理3.1
如果\(\epsilon\sim \mathcal{N}(0,\sigma^2I)\)，那么：

\[P_{X+\epsilon}(x)=\frac{1}{Z}\int_{\mathcal{M}}e^{-\frac{||y-x||^2}{2\sigma^2}}d\mathbb{P}_{X}(y) \]

定理3.2

推理3.2

定义3.1

引理4

定理3.3

定理3.3告诉我们一个有趣的idea。即上述式子中的两项是可以控制的。第一项可以通过噪音退火的方式来减少，第二项可以通过一个GAN（基于噪音输入来训练判别器）来最小化，因为他会近似于两个连续分布的JSD。该方法的一个优点是我们不再需要担心训练的选择方案。因为噪音，我们可以训练判别器直到最优而且没任何问题，并通过推理3.2得到平滑的可解释梯度。所有这一切仍然是在最小化\(\mathbb{P}_r\)和\(\mathbb{P}_g\)之间的距离，这两个分布也是我们最终关心的两个无噪声分布。

下面白话结论来自这里

• 原始GAN问题的根源可以归结为两点，一是等价优化的距离衡量（KL散度、JS散度）不合理，二是生成器随机初始化后的生成分布很难与真实分布有不可忽略的重叠。
• 本文其实已经针对第二点提出了一个解决方案，就是对生成样本和真实样本加噪声，直观上说，使得原本的两个低维流形“弥散”到整个高维空间，强行让它们产生不可忽略的重叠。而一旦存在重叠，JS散度就能真正发挥作用，此时如果两个分布越靠近，它们“弥散”出来的部分重叠得越多，JS散度也会越小而不会一直是一个常数，于是（在第一种原始GAN形式下）梯度消失的问题就解决了。在训练过程中，我们可以对所加的噪声进行退火（annealing），慢慢减小其方差，到后面两个低维流形“本体”都已经有重叠时，就算把噪声完全拿掉，JS散度也能照样发挥作用，继续产生有意义的梯度把两个低维流形拉近，直到它们接近完全重合。以上是对原文的直观解释。
• 在这个解决方案下我们可以放心地把判别器训练到接近最优，不必担心梯度消失的问题。而当判别器最优时，对公式26取反可得判别器的最小loss为

\[\begin{align} \min L_D(P_{r+\epsilon}, P_{g+\epsilon}) &= - \mathbb{E}_{x\sim P_{r+\epsilon}}\,\,[\log D^*(x)] - \mathbb{E}_{x\sim P_{g+\epsilon}}\,\,[\log(1-D^*(x))] \\ &= 2\log 2 - 2JS(P_{r+\epsilon} || P_{g+\epsilon}) \end{align}\]

其中\(P_{r+\epsilon}\)和\(P_{g+\epsilon}\)分别是加噪后的真实分布与生成分布。反过来说，从最优判别器的loss可以反推出当前两个加噪分布的JS散度。两个加噪分布的JS散度可以在某种程度上代表两个原本分布的距离，也就是说可以通过最优判别器的loss反映训练进程！……真的有这样的好事吗？
并没有，因为加噪JS散度的具体数值受到噪声的方差影响，随着噪声的退火，前后的数值就没法比较了，所以它不能成为\(P_r\)和\(P_g\)距离的本质性衡量。

• 加噪方案是针对原始GAN问题的第二点根源提出的，解决了训练不稳定的问题，不需要小心平衡判别器训练的火候，可以放心地把判别器训练到接近最优，但是仍然没能够提供一个衡量训练进程的数值指标。但是WGAN从第一点根源出发，用Wasserstein距离代替JS散度，同时完成了稳定训练和进程指标的问题！

WGAN前作分析了Ian Goodfellow提出的原始GAN两种形式各自的问题，第一种形式等价在最优判别器下等价于最小化生成分布与真实分布之间的JS散度，由于随机生成分布很难与真实分布有不可忽略的重叠以及JS散度的突变特性，使得生成器面临梯度消失的问题；第二种形式在最优判别器下等价于既要最小化生成分布与真实分布直接的KL散度，又要最大化其JS散度，相互矛盾，导致梯度不稳定，而且KL散度的不对称性使得生成器宁可丧失多样性也不愿丧失准确性，导致collapse mode现象。
WGAN前作针对分布重叠问题提出了一个过渡解决方案，通过对生成样本和真实样本加噪声使得两个分布产生重叠，理论上可以解决训练不稳定的问题，可以放心训练判别器到接近最优，但是未能提供一个指示训练进程的可靠指标，也未做实验验证。

references：

[1] L´eon Bottou, Frank E. Curtis, and Jorge Nocedal. Optimization methods for large-scale machine learning. CoRR, abs/1606.04838, 2016.
[2] Emily L. Denton, Soumith Chintala, Arthur Szlam, and Rob Fergus. Deep generative image models using a laplacian pyramid of adversarial networks. In Advances in Neural Information Processing Systems 28, pp. 1486–1494. Curran Associates, Inc., 2015.
[3] Ian J. Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, and Yoshua Bengio. Generative adversarial nets. In Advances in Neural Information Processing Systems 27, pp. 2672–2680. Curran Associates, Inc., 2014a.
[4] Ian J. Goodfellow, Jonathon Shlens, and Christian Szegedy. Explaining and harnessing adversarial examples. CoRR, abs/1412.6572, 2014b.
[5] Kurt Hornik. Approximation capabilities of multilayer feedforward networks. Neural Networks, 4 (2):251 – 257, 1991.
[6] Ferenc Huszar. How (not) to train your generative model: Scheduled sampling, likelihood, adversary? CoRR, abs/1511.05101, 2015.
[7] Ferenc Huszar. An alternative update rule for generative adversarial networks. Blogpost, 2016. URL http://www.inference.vc/an-alternative-update-rule-for-generative-adversarial-networks/.
[8] Diederik P. Kingma and Max Welling. Auto-encoding variational bayes. CoRR, abs/1312.6114, 2013.
[9] Alex Lamb, Anirudh Goyal, Ying Zhang, Saizheng Zhang, Aaron Courville, and Yoshua Bengio. Professor forcing: A new algorithm for training recurrent networks. Corr, abs/1610.09038, 2016.
[10] Hariharan Narayanan and Sanjoy Mitter. Sample complexity of testing the manifold hypothesis. In Advances in Neural Information Processing Systems 23, pp. 1786–1794. Curran Associates, Inc.,2010.
[11] Alec Radford, Luke Metz, and Soumith Chintala. Unsupervised representation learning with deep convolutional generative adversarial networks. CoRR, abs/1511.06434, 2015.
[12] Tim Salimans, Ian J. Goodfellow, Wojciech Zaremba, Vicki Cheung, Alec Radford, and Xi Chen. Improved techniques for training gans. CoRR, abs/1606.03498, 2016.
[13] Lucas Theis, Aaron van den Oord, and Matthias Bethge. A note on the evaluation of generative models. In International Conference on Learning Representations, Apr 2016.
[14] C´edric Villani. Optimal Transport: Old and New. Grundlehren der mathematischen Wissenschaften. Springer, Berlin, 2009. ISBN 978-3-540-71049-3. URL http://opac.inria.fr/record=b1129524.
[15] Jiajun Wu, Chengkai Zhang, Tianfan Xue, William T. Freeman, and Joshua B. Tenenbaum. Learning a probabilistic latent space of object shapes via 3d generative-adversarial modeling. Corr,abs/1610.07584, 2016. 14
[16] GAN（Generative Adversarial Network）的学习历程
[17] Wasserstein GANs 三部曲（一）：Towards Principled Methods for Training Generative Adversarial Networks的理解
[18] ICML 2017大熱論文：Wasserstein GAN
[19] 【GAN 货】生成式对抗网络资料荟萃（原理/教程/报告/论文/实战/资料库）
[20] 生成对抗网络——FGAN和WGAN
[21] WGAN和GAN直观区别和优劣
[22] 令人拍案叫绝的Wasserstein GAN