Python实现线性回归之 一元线性回归and平方损失函数

线性回归是一种较为简单，但十分重要的机器学习方法。掌握线性的原理及求解方法，是深入了解线性回归的基本要求。除此之外，线性回归也是监督学习的基石，希望你能最终掌握机器学习的一些重要的思想。
今天就给大家展开讲讲线性回归里的一元线性回归和平方损失函数。

线性回归介绍

回归问题旨在实现对连续值的预测，例如股票的价格、房价的趋势等。比如，下方展现了一个房屋面积和价格的对应关系图。

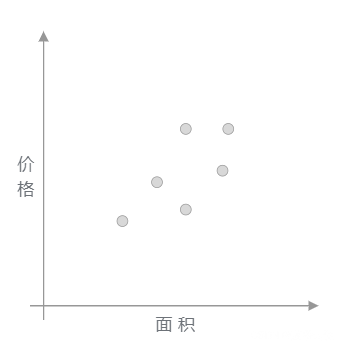
如上图所示，不同的房屋面积对应着不同的价格。现在，假设我手中有一套房屋想要出售，而出售时就需要预先对房屋进行估值。于是，我想通过上图，也就是其他房屋的售价来判断手中的房产价值是多少。应该怎么做呢？

我采用的方法是这样的。如下图所示，首先画了一条红色的直线，让其大致验证数据色点分布的延伸趋势。然后，我将已知房屋的面积大小对应到红色直线上，也就是蓝色点所在位置。最后，再找到蓝色点对应于房屋的价格作为房屋最终的预估价值。

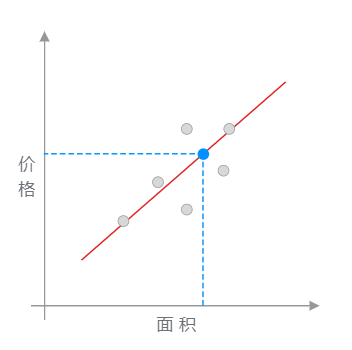
在上图呈现的这个过程中，通过找到一条直线去拟合数据点的分布趋势的过程，就是线性回归的过程。而线性回归中的「线性」代指线性关系，也就是图中所绘制的红色直线。
此时，你可能心中会有一个疑问。上图中的红色直线是怎么绘制出来的呢？为什么不可以像下图中另外两条绿色虚线，而偏偏要选择红色直线呢？

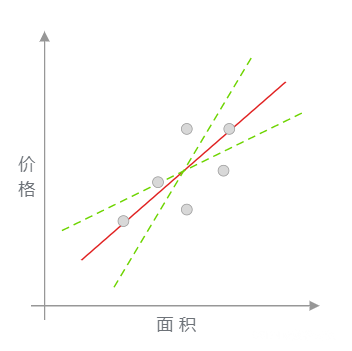
绿色虚线的确也能反应数据点的分布趋势。所以，找到最适合的那一条红色直线，就成为了线性回归中需要解决的目标问题。

通过上面这个小例子，相信你对线性回归已经有一点点印象了，至少大致明白它能做什么。接下来的内容中，我们将了解线性回归背后的数学原理，以及使用 Python 代码对其实现。

一元线性回归

上面针对 线性回归 的介绍内容中，我们列举了一个房屋面积与房价变化的例子。其中，房屋面积为自变量，而房价则为因变量。另外，我们将只有 1 个自变量的线性拟合过程叫做一元线性回归。

下面，我们就生成一组房屋面积和房价变化的示例数据。𝑥 为房屋面积，单位是平方米; 𝑦 为房价，单位是万元。

import numpy as np

x = np.array([56, 72, 69, 88, 102, 86, 76, 79, 94, 74])
y = np.array([92, 102, 86, 110, 130, 99, 96, 102, 105, 92])

示例数据由 10 组房屋面积及价格对应组成。接下来，通过 Matplotlib 绘制数据点， 𝑥 , 𝑦 分别对应着横坐标和纵坐标。

from matplotlib import pyplot as plt
%matplotlib inline

plt.scatter(x, y)
plt.xlabel("Area")
plt.ylabel("Price")

正如上面所说，线性回归即通过线性方程去拟合数据点。那么，我们可以令该 1 次函数的表达式为：

\[y(x, w) = w_0 + w_1x \tag{1} \]

公式 \((1)\) 是典型的一元一次函数表达式，我们通过组合不同的 \(w_0\) 和 \(w_1\) 的值得到不同的拟合直线。
接下来，对公式 \((1)\) 进行代码实现：

def f(x: list, w0: float, w1: float):
    """一元一次函数表达式
    """
    y = w0 + w1 * x
    return y

那么，哪一条直线最能反应出数据的变化趋势呢？

想要找出对数据集拟合效果最好的直线，这里再拿出上小节图示进行说明。如下图所示，当我们使用 \(y(x, w) = w_0 + w_1x\) 对数据进行拟合时，就能得到拟合的整体误差，即图中蓝色线段的长度总和。如果某一条直线对应的误差值最小，是不是就代表这条直线最能反映数据点的分布趋势呢？

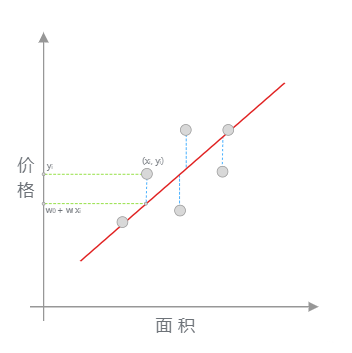
平方损失函数

正如上面所说，如果一个数据点为 (\(x_{i}\), \(y_{i}\))，那么它对应的误差就为:

\[y_{i}-(w_0 + w_1x_{i}) \tag{2} \]

上面的误差往往也称之为「残差」。但是在机器学习中，我们更喜欢称作「损失」，即真实值和预测值之间的偏离程度。那么，对 \(n\) 个全部数据点而言，其对应的残差损失总和就为：

\[\sum\limits_{i = 1}^n {{{(y_{i}-(w_0 + w_1x_{i}))}}} \tag{3} \]

更进一步，在线性回归中，我们一般使用残差的平方和来表示所有样本点的误差。公式如下：

\[\sum\limits_{i = 1}^n {{{(y_{i}-(w_0 + w_1x_{i}))}}^2} \tag{4} \]

使用残差平方和的好处在于能保证损失始终是累加的正数，而不会存在正负残差抵消的问题。对于公式 \((4)\) 而言，机器学习中有一个专门的名词，那就是「平方损失函数」。而为了得到拟合参数 \(w_0\) 和 \(w_1\) 最优的数值，我们的目标就是让公式 \((4)\) 对应的平方损失函数最小。
同样，我们可以对公式 \((4)\) 进行代码实现：

def square_loss(x: np.ndarray, y: np.ndarray, w0: float, w1: float):
    """平方损失函数
    """
    loss = sum(np.square(y - (w0 + w1 * x)))
    return loss

如果某条直线拟合样本得到的总损失最小，那么这条直线就是最终想得到的结果。而求解损失最小值的过程，就必须用到下面的数学方法了。

参考资料
如果对你有帮助就点个赞吧！