大多数都是递推关系,其中很大的一个应用就是fibonacci数列
难点其实在于构造适当的矩阵,以下是一些应用
(1)线性齐次及非齐次递推式的快速求项,求和
(2)计算几何中点和图形的坐标(旋转,平移,伸压)变换
(3)不涉及插入、删除的点变换,区间变换和查询
(4)图论中的路径数问题
(5)dp的优化之线性递推方程优化(本质和(1)是一样的)
(6)dp及AC自动机之状态优化(将状态看作图上的点,转移看作边,本质和(1)是一样的)
【一本通的题】
1641: 【例 1】矩阵 A×B
very very 简单的一道题
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=1010;
const int INF=0x3fffffff;
typedef long long LL;
typedef unsigned long long ull;
int n,m,p;
LL a[110][110],b[110][110],c[110][110];
int main(){
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++) scanf("%lld",&a[i][j]);
scanf("%d",&p);
for(int i=1;i<=m;i++)
for(int j=1;j<=p;j++) scanf("%lld",&b[i][j]);
for(int i=1;i<=n;i++){ //最外面的两次是最后结果矩阵的大小
for(int j=1;j<=p;j++){
for(int z=1;z<=m;z++){
c[i][j]+=a[i][z]*b[z][j];
}
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=p;j++) printf("%lld ",c[i][j]);
printf("\n");
}
return 0;
}
1642: 【例 2】Fibonacci 第 n 项
这个就是模板题了
初始矩阵是 1 0
转移矩阵是1 1
1 0
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=1010;
const int INF=0x3fffffff;
typedef long long LL;
typedef unsigned long long ull;
//这个是模板
//斐波那契数列取模
/*
(1)
1 0 * 1 1 = 1 1
1 0
(2)
1 1 * 1 1 = 2 1
1 0
(3)
2 1 * 1 1 = 3 2
1 0
所以第n项就是1 0 * (1,1)^n
(1,0)
用快速幂优化就是矩阵快速幂了
*/
LL n,mod;
LL a[3][3],b[3][3],ans[3][3],c[3][3];
void add(LL &x,LL y){
x=x+y;
x-=(x>=mod)?mod:0;
return;
}
// memmove用于拷贝字节,如果目标区域和源区域有重叠的话,memmove能够保证源串在被覆盖之前将重叠区域的字节拷贝到目标区域中,但复制后源内容会被更改。
//但是当目标区域与源区域没有重叠则和memcpy函数功能相同。
int main(){
scanf("%lld %lld",&n,&mod);
n-=1;
a[1][1]=a[1][2]=a[2][1]=1;a[2][2]=0;
ans[1][1]=ans[2][2]=1; //ans是单位矩阵
ans[2][1]=ans[1][2]=0;
while(n){
if(n&1){ //快速幂
memset(c,0,sizeof(c));
for(int i=1;i<=2;i++){
for(int j=1;j<=2;j++){
for(int k=1;k<=2;k++) add(c[i][j],ans[i][k]*a[k][j]%mod);
}
}
memmove(ans,c,sizeof(ans)); //这个函数是实现字节的拷贝 把c放在ans里面
}
memset(c,0,sizeof(c));
//对a进行倍乘
for(int i=1;i<=2;i++)
for(int j=1;j<=2;j++){
for(int k=1;k<=2;k++) add(c[i][j],a[i][k]*a[k][j]%mod);
}
memmove(a,c,sizeof(a));
n>>=1;
}
//这个快速幂主要目的是求出ans数组,然后最后直接与b相乘
b[1][1]=1;b[1][2]=0;
memset(c,0,sizeof(c));
for(int i=1;i<=1;i++){ //最后大小是1*2
for(int j=1;j<=2;j++){
for(int k=1;k<=2;k++) add(c[i][j],ans[i][k]*b[k][j]);
}
}
memmove(b,c,sizeof(b));
printf("%lld\n",b[1][1]);
return 0;
}
1643:【例 3】Fibonacci 前 n 项和
1 0 0
1 1 1
1 1 0 这个是应该乘的转移矩阵
第一个矩阵是 1 1 0 第一位是到i的和,第二位是fi-1,第三位是fi-2),每次乘右边这个矩阵就是转移一次
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=1010;
const int INF=0x3fffffff;
typedef long long LL;
typedef unsigned long long ull;
/*
1 0 0
1 1 1
1 1 0 这个是应该乘的转移矩阵
第一个矩阵式 1 1 0 第一位是到i的和,第二位是fi-1,第三位是fi-2),每次乘右边这个矩阵就是转移一次
*/
int n;
LL power[5][5],a[5][5],c[5][5],ans[5][5];
LL mod;
void add(LL &x,LL y){
x+=y;
if(x>=mod) x-=mod;
return;
}
int main(){
scanf("%d",&n);
n-=1; //因为第一项和第二项都是1
scanf("%lld",&mod);
ans[1][1]=ans[1][2]=1; //ans[1][3]=0
a[1][1]=a[2][1]=a[2][2]=a[2][3]=a[3][1]=a[3][2]=1;
for(int i=1;i<=3;i++) power[i][i]=1;
//单位矩阵
while(n){ //计算ans数组
if(n&1){
memset(c,0,sizeof(c));
for(int i=1;i<=3;i++)
for(int j=1;j<=3;j++)
for(int k=1;k<=3;k++){
add(c[i][j],power[i][k]*a[k][j]%mod);
}
memmove(power,c,sizeof(power));
}
memset(c,0,sizeof(c));
for(int i=1;i<=3;i++)
for(int j=1;j<=3;j++)
for(int k=1;k<=3;k++){
add(c[i][j],a[i][k]*a[k][j]%mod);
}
memmove(a,c,sizeof(a));
n>>=1;
}
memset(c,0,sizeof(c));
for(int i=1;i<=1;i++){
for(int j=1;j<=3;j++)
for(int k=1;k<=3;k++) add(c[i][j],ans[i][k]*power[k][j]%mod);
}
memmove(ans,c,sizeof(c));
printf("%lld\n",ans[1][1]);
return 0;
}
1644:【例 4】佳佳的 Fibonacci

这个数组有不一样的了
我完全想不到。。。。
https://www.cnblogs.com/henry-1202/p/9932349.html
还有这个转移矩阵(人家随随便便就推出来了。。。
p[i] 1 1 0 0 p[i+1]
s[i] 0 1 1 0 s[i+1]
f[i] 0 0 1 1 f[i+1]
f[i-1]0 0 1 0 f[i]
f[i] = f[i-1]+f[i-2]
T[n] = f[1]+f[2]*2+f[3]*3+...+f[n]*n
S[n] = f[1]+f[2]+f[3]+...+f[n]
n*S[n] = n*f[1]+n*f[2]+n*f[3]+...+n*f[n]
设
--> P[n] = n*S[n]-T[n]
--> P[n] = (n-1)*f[1]+(n-2)*f[2]+...+(n-n)*f[n]
因为
--> P[n-1] = (n-1)*S[n]-T[n-1]
--> P[n-1] = (n-2)*f[1]+(n-3)*f[2]+...+(n-1-(n-1))*f[n-1]
且
--> S[n-1] = f[1]+f[2]+f[3]+....+f[n-1]
所以
P[n]=P[n-1]+S[n-1]
P[i] S[i] f[i] f[i-1]
1 0 0 0
1 1 0 0
0 1 1 1
0 1 1 0
*/
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=1010;
const int INF=0x3fffffff;
typedef long long LL;
typedef unsigned long long ull;
//我完全想不到。。。。
//https://www.cnblogs.com/henry-1202/p/9932349.html
/*
还有这个转移矩阵(人家随随便便就推出来了。。。
p[i] 1 1 0 0 p[i+1]
s[i] 0 1 1 0 s[i+1]
f[i] 0 0 1 1 f[i+1]
f[i-1]0 0 1 0 f[i]
f[i] = f[i-1]+f[i-2]
T[n] = f[1]+f[2]*2+f[3]*3+...+f[n]*n
S[n] = f[1]+f[2]+f[3]+...+f[n]
n*S[n] = n*f[1]+n*f[2]+n*f[3]+...+n*f[n]
设
--> P[n] = n*S[n]-T[n]
--> P[n] = (n-1)*f[1]+(n-2)*f[2]+...+(n-n)*f[n]
因为
--> P[n-1] = (n-1)*S[n]-T[n-1]
--> P[n-1] = (n-2)*f[1]+(n-3)*f[2]+...+(n-1-(n-1))*f[n-1]
且
--> S[n-1] = f[1]+f[2]+f[3]+....+f[n-1]
所以
P[n]=P[n-1]+S[n-1]
P[i] S[i] f[i] f[i-1]
1 0 0 0
1 1 0 0
0 1 1 1
0 1 1 0
*/
LL n,mod;
LL ans[5][5],power[5][5],a[5][5],c[5][5];
void add(LL &x,LL y){
x+=y;
if(x>=mod) x-=mod;
return;
}
int main(){
scanf("%lld",&n);
int nn=n;
n-=1;
scanf("%lld",&mod);
ans[1][2]=ans[1][3]=1;//0 1 1 0
for(int i=1;i<=4;i++) {
power[i][i]=1; //单位矩阵
}
a[1][1]=a[2][2]=a[2][1]=a[3][2]=a[3][3]=a[3][4]=a[4][2]=a[4][3]=1;
while(n){
if(n&1){
memset(c,0,sizeof(c));
for(int i=1;i<=4;i++)
for(int j=1;j<=4;j++)
for(int k=1;k<=4;k++)
add(c[i][j],power[i][k]*a[k][j]%mod);
memmove(power,c,sizeof(power));
}
memset(c,0,sizeof(c));
for(int i=1;i<=4;i++)
for(int j=1;j<=4;j++)
for(int k=1;k<=4;k++)
add(c[i][j],a[i][k]*a[k][j]%mod);
memmove(a,c,sizeof(a));
n>>=1;
}
memset(c,0,sizeof(c));
for(int i=1;i<=1;i++)
for(int j=1;j<=4;j++)
for(int k=1;k<=4;k++)
add(c[i][j],ans[i][k]*power[k][j]%mod);
memmove(ans,c,sizeof(ans));
//结果是ns[n]-p[n]
printf("%lld",(ans[1][2]*nn%mod-ans[1][1]+mod)%mod);
return 0;
}
1645:Fibonacci
没啥变化还是模板题,就是数据多组,不用看了
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=1010;
const int INF=0x3fffffff;
typedef long long LL;
typedef unsigned long long ull;
//这个是模板
//斐波那契数列取模
/*
(1)
1 0 * 1 1 = 1 1
1 0
(2)
1 1 * 1 1 = 2 1
1 0
(3)
2 1 * 1 1 = 3 2
1 0
所以第n项就是1 0 * (1,1)^n
(1,0)
用快速幂优化就是矩阵快速幂了
*/
LL n,mod;
LL a[3][3],b[3][3],ans[3][3],c[3][3];
void add(LL &x,LL y){
x=x+y;
x-=(x>=mod)?mod:0;
return;
}
// memmove用于拷贝字节,如果目标区域和源区域有重叠的话,memmove能够保证源串在被覆盖之前将重叠区域的字节拷贝到目标区域中,但复制后源内容会被更改。
//但是当目标区域与源区域没有重叠则和memcpy函数功能相同。
int main(){
mod=10000;
while(~scanf("%lld",&n)){
if(n==0){
printf("0\n");
continue;
}
if(n==-1) break;
n-=1;
a[1][1]=a[1][2]=a[2][1]=1;a[2][2]=0;
ans[1][1]=ans[2][2]=1; //ans是单位矩阵
ans[2][1]=ans[1][2]=0;
while(n){
if(n&1){ //快速幂
memset(c,0,sizeof(c));
for(int i=1;i<=2;i++){
for(int j=1;j<=2;j++){
for(int k=1;k<=2;k++) add(c[i][j],ans[i][k]*a[k][j]%mod);
}
}
memmove(ans,c,sizeof(ans)); //这个函数是实现字节的拷贝 把c放在ans里面
}
memset(c,0,sizeof(c));
//对a进行倍乘
for(int i=1;i<=2;i++)
for(int j=1;j<=2;j++){
for(int k=1;k<=2;k++) add(c[i][j],a[i][k]*a[k][j]%mod);
}
memmove(a,c,sizeof(a));
n>>=1;
}
//这个快速幂主要目的是求出ans数组,然后最后直接与b相乘
b[1][1]=1;b[1][2]=0;
memset(c,0,sizeof(c));
for(int i=1;i<=1;i++){ //最后大小是1*2
for(int j=1;j<=2;j++){
for(int k=1;k<=2;k++) add(c[i][j],ans[i][k]*b[k][j]);
}
}
memmove(b,c,sizeof(b));
printf("%lld\n",b[1][1]);
}
return 0;
}
1646:GT 考试
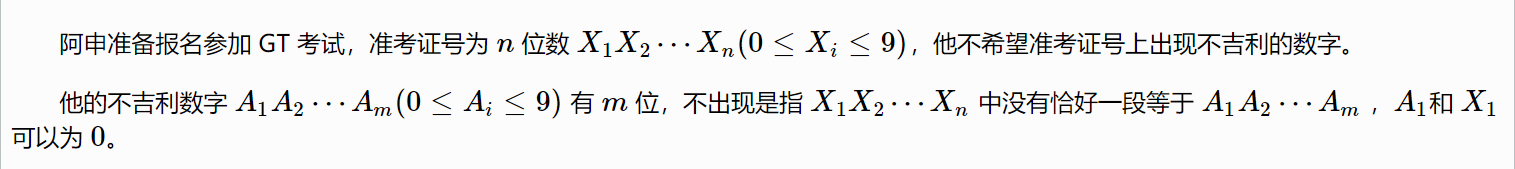
![]()
这个应该属于第(5)种,先推出dp方程式,然后用矩阵快速幂去优化
https://blog.csdn.net/jianglw1/article/details/98247505
https://www.cnblogs.com/gaojunonly1/p/10507823.html
这个解释德比较清楚,但是我还是没看懂,匹配那一部分,为什么要用到KMP
此题应该是先想到暴力的做法再用矩阵乘法优化的
所以暴力的思想很重要
dp[i][j]表示到第i位,匹配了j个的方案数
先预处理出f[i][j]表示已经匹配了i个,加一个数字变成匹配了j个方案数,i,j<=m-1,用kmp搞搞
转移就不难了,dp[i][j]+=dp[i-1][k]*f[k][j] 和矩阵乘法很像


#include <bits/stdc++.h>
using namespace std;
typedef int ll;
/*
https://blog.csdn.net/jianglw1/article/details/98247505
https://www.cnblogs.com/gaojunonly1/p/10507823.html
这个解释德比较清楚,但是我还是没看懂,匹配那一部分,为什么要用到KMP
此题应该是先想到暴力的做法再用矩阵乘法优化的
所以暴力的思想很重要
dp[i][j]表示到第i位,匹配了j个的方案数
先预处理出f[i][j]表示已经匹配了i个,加一个数字变成匹配了j个方案数,i,j<=m-1,用kmp搞搞
转移就不难了,dp[i][j]+=dp[i-1][k]*f[k][j] 和矩阵乘法很像
*/
inline ll read()
{
ll s=0;
bool f=0;
char ch=' ';
while(!isdigit(ch))
{
f|=(ch=='-'); ch=getchar();
}
while(isdigit(ch))
{
s=(s<<3)+(s<<1)+(ch^48); ch=getchar();
}
return (f)?(-s):(s);
}
#define R(x) x=read()
inline void write(ll x)
{
if(x<0)
{
putchar('-'); x=-x;
}
if(x<10)
{
putchar(x+'0'); return;
}
write(x/10);
putchar((x%10)+'0');
return;
}
#define W(x) write(x),putchar(' ')
#define Wl(x) write(x),putchar('\n')
const int N=100005,M=25;
int n,m,Mod;
int Num[25],f[25][25];
int ans[25][25],power[25][25],a[25][25],c[25][25];
inline void Ad(int &x,int y)
{
x+=y;
x-=(x>=Mod)?Mod:0;
return;
}
int Next[25];
inline void Pre_f()
{
int i,j=0;
Next[1]=0;
for(i=2;i<=m;i++)
{
while((Num[j+1]!=Num[i])&&j) j=Next[j];
if(Num[j+1]==Num[i]) j++;
Next[i]=j;
}
for(i=0;i<m;i++)
{
for(j=0;j<=9;j++)
{
int Now=i;
while((Num[Now+1]!=j)&&Now) Now=Next[Now];
if(Num[Now+1]==j) Now++;
f[i][Now]++;
}
}
/*
for(i=0;i<m;i++,puts(""))
{
for(j=0;j<m;j++) W(f[i][j]);
}
puts("");
*/
return;
}
int main()
{
int i,j,k,Sum=0;
R(n); R(m); R(Mod);
for(i=1;i<=m;i++)
{
char ch=' ';
while(!isdigit(ch)) ch=getchar();
Num[i]=ch-'0';
}
Pre_f();
ans[0][0]=1;
for(i=0;i<=m-1;i++) power[i][i]=1;
memmove(a,f,sizeof a);
while(n)
{
if(n&1)
{
memset(c,0,sizeof c);
for(i=0;i<=m-1;i++) for(j=0;j<=m-1;j++) for(k=0;k<=m-1;k++)
{
Ad(c[i][j],power[i][k]*a[k][j]%Mod);
}
memmove(power,c,sizeof power);
}
memset(c,0,sizeof c);
for(i=0;i<=m-1;i++) for(j=0;j<=m-1;j++) for(k=0;k<=m-1;k++)
{
Ad(c[i][j],a[i][k]*a[k][j]%Mod);
}
memmove(a,c,sizeof a);
n>>=1;
}
memset(c,0,sizeof c);
for(i=0;i<=0;i++) for(j=0;j<=m-1;j++) for(k=0;k<=m-1;k++)
{
Ad(c[i][j],ans[i][k]*power[k][j]%Mod);
}
memmove(ans,c,sizeof ans);
for(i=0;i<m;i++) Ad(Sum,ans[0][i]);
Wl(Sum);
return 0;
}
1647:迷路

这个就是类型(4)图论中的题
其实这里要先知道一个结论的,我不知道TAT
这个题初看没有什么头绪(dp失败. 我们联系一下邻接矩阵,
邻接矩阵一个很神奇的性质: 表示连通性的邻接矩阵的k次幂后的a[i][j]表示图中i–>j长度为k的路径条数,大概理解为:
从第i点出发到任意点的长度k-1道路条数(第i行) 与 任意点到j点的长度1的道路条数(第j列) 乘积和就是i–>j长度为k的路径条数
, 但是邻接矩阵只能处理边权为1的点, 这题需要转换. 我们把一个点i拆成更多的虚点,用来抵消部分边权的距离, 让它实际上以邻接矩阵的方式跑图. 假如点1到点2的边权为5,
把这条边拆成边权为1的5条边, 让点1在自己的虚点上先走4步, 最后到达2, 路径(1.0)->(1.1)->(1.2)->(1.3)->(1.4)->(2.0), 最后矩阵快速幂一下。
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=505;
const int INF=0x3fffffff;
typedef long long LL;
typedef unsigned long long ull;
//https://www.cnblogs.com/gaojunonly1/p/10507823.html
//https://blog.csdn.net/jianglw1/article/details/98247593
/*
这个题初看没有什么头绪(dp失败. 我们联系一下邻接矩阵, 邻接矩阵一个很神奇的性质: 表示连通性的邻接矩阵的k次幂后的a[i][j]表示图中i–>j长度为k的路径条数,大概理解为:
从第i点出发到任意点的长度k-1道路条数(第i行) 与 任意点到j点的长度1的道路条数(第j列) 乘积和就是i–>j长度为k的路径条数
? 但是邻接矩阵只能处理边权为1的点, 这题需要转换. 我们把一个点i拆成更多的虚点,用来抵消部分边权的距离, 让它实际上以邻接矩阵的方式跑图. 假如点1到点2的边权为5,
把这条边拆成边权为1的5条边, 让点1在自己的虚点上先走4步, 最后到达2, 路径(1.0)->(1.1)->(1.2)->(1.3)->(1.4)->(2.0), 最后矩阵快速幂一下。
*/
int n,m,mod=2009,t;
struct node{
int mp[105][105];
node(){
memset(mp,0,sizeof(mp));
}
node operator * (const node &tt)const{
node ans;
for(int i=1;i<=m;i++)
for(int j=1;j<=m;j++)
for(int k=1;k<=m;k++)
ans.mp[i][j]=(ans.mp[i][j]+mp[i][k]*tt.mp[k][j]%mod)%mod;
return ans;
}
};
node poww(node a,int k){
node res;
for(int i=1;i<=m;i++) res.mp[i][i]=1;
while(k){
if(k&1){
res=res*a;
}
a=a*a;
k>>=1;
}
return res;
}
int main(){
scanf("%d %d",&n,&t);
m=9*n;
//总共的点数!!
node ans,base;
for(int i=1;i<=n;i++){ //每个点都拆为9个
for(int j=1;j<9;j++){
base.mp[(i-1)*9+j][(i-1)*9+j+1]=1; //连接拆点
}
}
int tmp;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
scanf("%1d",&tmp); //!!!!!!!!这里,保证输入这个数只有一位!!!
if(tmp){
base.mp[(i-1)*9+tmp][(j-1)*9+1]=1; //在自己的链上跑tmp次到下个状态
}
}
}
ans=poww(base,t);
printf("%d\n",ans.mp[1][m-8]);
//最后一个点的1.0
return 0;
}
POJ 3735 Training little cats
//其实这是一道理解转移矩阵很好的一道题
//g 给1个 e 吃掉所以 s(i,j) 交换i和j的
/*
1 0 0 1 x ---> x+1
0 1 0 0 y ---> y
0 0 1 0 z ---> z
0 0 0 1 1 ---> 1
1 0 0 0 x ---> x
0 0 0 0 y ---> 0
0 0 1 0 z ---> z
0 0 0 1 1 ---> 1
1 0 0 0 x ---> x
0 0 1 0 y ---> z
0 1 0 0 z ---> y
0 0 0 1 1 ---> 1
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=110;
const int INF=0x3fffffff;
typedef long long LL;
typedef unsigned long long ull;
//其实这是一道理解转移矩阵很好的一道题
//g 给1个 e 吃掉所以 s(i,j) 交换i和j的
/*
1 0 0 1 x ---> x+1
0 1 0 0 y ---> y
0 0 1 0 z ---> z
0 0 0 1 1 ---> 1
1 0 0 0 x ---> x
0 0 0 0 y ---> 0
0 0 1 0 z ---> z
0 0 0 1 1 ---> 1
1 0 0 0 x ---> x
0 0 1 0 y ---> z
0 1 0 0 z ---> y
0 0 0 1 1 ---> 1
*/
struct node{
LL mp[maxn][maxn];
node(){
memset(mp,0,sizeof(mp));
}
};
node e,ans;
int n,m,k;
node mul(node a,node b){
node res;
for(int i=0;i<=n;i++){
for(int j=0;j<=n;j++){
if(a.mp[i][j]) //优化,不然会超时
for(int k=0;k<=n;k++){
res.mp[i][k]+=(a.mp[i][j]*b.mp[j][k]);
}
}
}
return res;
}
//快速幂
node ksm(node a,int k){
node res;
for(int i=0;i<=n;i++) res.mp[i][i]=1;
while(k){
if(k&1){
res=mul(res,a);
}
a=mul(a,a);
k>>=1;
}
return res;
}
void inti(){
char w[2];
memset(e.mp,0,sizeof(e.mp));
//初始化为单位矩阵
int x,y;
for(int i=0;i<=n;i++) e.mp[i][i]=1;
while(k--){
scanf("%s",w);
if(w[0]=='g'){ //给一个
scanf("%d",&x);
x--; //eieieieieieiattention
e.mp[n][x]++;
}
else if(w[0]=='e'){ //吃完
scanf("%d",&x);
x--;
for(int i=0;i<=n;i++) e.mp[i][x]=0; //都要清0
}
else {
scanf("%d %d",&x,&y);
x--;y--;
if(x!=y){
for(int i=0;i<=n;i++){
swap(e.mp[i][x],e.mp[i][y]);
}
}
}
}
}
int main(){
while(~scanf("%d %d %d",&n,&m,&k)){
if(n==0&&m==0&&k==0) break;
inti();
ans=ksm(e,m); //变换矩阵做m次变化
for(int i=0;i<n;i++){
printf("%lld ",ans.mp[n][i]); //输出前n个
}
printf("\n");
}
return 0;
}


 posted on
posted on

 浙公网安备 33010602011771号
浙公网安备 33010602011771号