组合数学
研究一个集合内满足一定规则的排列问题
(1)存在问题,判断排列是否存在
(2)计数问题,计算出有多少个排列
(3)优化问题
包括很多很多question:
1、基本计数规则:乘法规则、加法规则、生成排列组合、多项式系数、抽屉原理、
2、计数问题:母函数(普通型、指数型、概率型)、二项式定理、递推关系、容斥原理、polya原理
3、存在问题:编码、组合设计、图论中的存在问题
4、组合优化:匹配和覆盖、图和网络的优化问题
-----------截图都是董老师------------yyds
1.排列
- 线排列:p(n,m)=n!/(n-m)!
- 相异元素可重复排列:n^m
- 不全相异元素排列:元素1有n1个,元素2有n个..... n!/(n1!)/(n2)!/....../(nm)!
- 圆排列:排成首尾相接的圈:p(n,m)/m
2、组合
C(n,m)=n!/m!(n-m)!
C(n,m)=C(n,n-m)
C(n,m)=C(n-1,m)+C(n-1,m-1)
可重复组合 H(n,r)=C(n+r-1,r)
ps:注意数据范围
(1)利用递推公式,数据范围比较小
const int N=2010, P=1e9+7; int C[N][N]; void init(){ for(int i=0; i<N; i++) C[i][0] = 1; for(int i=1; i<N; i++) for(int j=1; j<=i; j++) C[i][j]=(C[i-1][j]+C[i-1][j-1])%P; }
(2)利用乘法逆元

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long LL;
const int maxn=1005;
const int N=100010, mod=1e9+7;
LL f[N],g[N];
LL qpow(LL a,int b){
LL res=1;
while(b){
if(b&1) res=res*a%mod;
a=a*a%mod;
b>>=1;
}
return res;
}
void inti(){
f[0]=g[0]=1;
for(int i=1;i<N;i++){
f[i]=f[i-1]*i%mod;
g[i]=g[i-1]*qpow(i,mod-2)%mod;
}
}
int getC(LL n,LL m){
return f[n]*g[m]%mod*g[n-m]%mod;
}
int main(){
inti();
int q,n,m;
cin>>q;
while(q--){
cin>>n>>m;
cout<<getC(n,m)<<endl;
}
}
(3)大组合数取模问题:lucas定理

https://www.luogu.com.cn/problem/P3807 P3807 【模板】卢卡斯定理/Lucas 定理
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long LL;
const int maxn=1005;
const int N=100010;
LL f[N],g[N];
LL qpow(LL a,int b,int p){
LL res=1;
while(b){
if(b&1) res=res*a%p;
a=a*a%p;
b>>=1;
}
return res;
}
void inti(int p){
g[0]=f[0]=1;
for(int i=1;i<=p;i++){
f[i]=f[i-1]*i%p;
g[i]=g[i-1]*qpow(i,p-2,p)%p;
}
}
LL getC(int n,int m,int p){
return f[n]*g[m]*g[n-m]%p;
}
int lucas(LL n,LL m,int p){
if(m==0) return 1;
return lucas(n/p,m/p,p)*getC(n%p,m%p,p)%p;
}
int main(){
int q,n,m,p;
cin>>q;
while(q--){
cin>>n>>m>>p;
inti(p);
printf("%d\n",lucas(n+m,n,p));
}
return 0;
}
(4)(没有模),用高精度,还有质因子分解

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 10010;
int prim[N], vis[N], cnt;
void get_prim(int n){ //筛素数
for(int i = 2; i <= n; i ++){
if(!vis[i]) prim[cnt++] = i;
for(int j=0; i*prim[j]<=n; j++){
vis[i*prim[j]] = 1;
if(i%prim[j] == 0) break;
}
}
}
int get(int n,int p){ //n!中p的个数
int s = 0;
while(n) s += n/p, n /= p;
return s;
}
int getps(int n,int m,int p){//C中p的个数
return get(n,p)-get(m,p)-get(n-m,p);
}
void mul(int C[],int p,int &len){//高精度
int t = 0;
for(int i=0; i<len; i++){
t += C[i]*p;
C[i] = t%10;
t /= 10;
}
while(t){
C[len++] = t%10;
t /= 10;
}
}
int main(){
int n, m;
cin >> n >> m;
get_prim(n);
int C[N], len=1; C[0]=1;
for(int i=0; i<cnt; i++){
int p = prim[i];
int s = getps(n,m,p);
while(s--) mul(C,p,len);
}
for(int i=len-1; i>=0; i--)
printf("%d", C[i]);
return 0;
}
3、杨辉三角和二项式系数
Cnk---(二项式定理)-----(1+x)^n------杨辉三角第n行
1648:【例 1】「NOIP2011」计算系数
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const int maxn=1005;
typedef long long LL;
int c[maxn][maxn];
int n,m,a,b,k;
int mod=10007;
int main(){
cin>>a>>b>>k>>n>>m;
for(int i=1;i<=k;i++){ //利用杨辉三角求出二项式系数
c[i][0]=c[i][i]=1;
for(int j=1;j<=i-1;j++) c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;
}
int ans=c[k][m];
a%=mod;b%=mod;
int aa=1,bb=1;
for(int i=1;i<=n;i++) aa=aa*a%mod;
for(int j=1;j<=m;j++) bb=bb*b%mod;
ans=ans*aa%mod*bb%mod;
cout<<ans<<endl;
return 0;
}
4 抽屉原理(鸽巢原理)---ramsey原理特列

https://www.luogu.com.cn/problem/P1771 P1771 方程的解

1、快速幂求出n=x^x(mod1000)结果
2、利用隔板法知道答案为C(n-1,k-1),这里直接递推就可以
3、但是注意C(1000,100)有140位,所以要用到高精度
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
typedef long long ll;
const int maxn=150,p=1000;
int c[1000][100][maxn]; //高精度
int qpow(int a,int b){
int x=1;
while(b){
if(b&1) x=x*a%p;
a=a*a%p;
b>>=1;
}
return x;
}
void add(int cc[],int a[],int b[]){
for(int i=0;i<maxn;i++){
cc[i]+=a[i]+b[i];
cc[i+1]+=cc[i]/10;
cc[i]%=10;
}
}
void getc(int n,int k){
for(int i=0;i<n;i++){
for(int j=0;j<=i&&j<k;j++){
if(j==0) c[i][j][0]=1;
else add(c[i][j],c[i-1][j],c[i-1][j-1]);
}
}
}
int main(){
int k,x;
cin>>k>>x;
int n=qpow(x%p,x);
getc(n,k);
int i=maxn-1;
while(c[n-1][k-1][i]==0) i--;
while(i>=0) cout<<c[n-1][k-1][i--];
return 0;
}
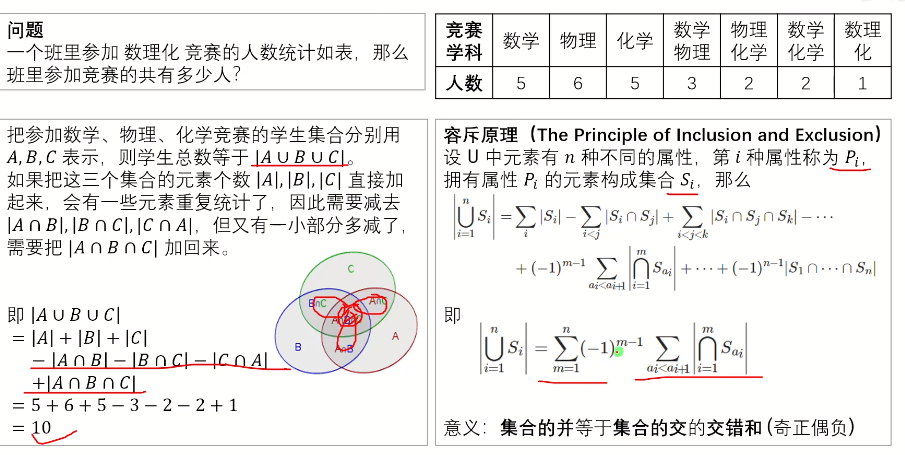
5、 容斥原理
集合的并、集合的交的情况问题
1、集合的并

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long ll;
const int maxn=20;
int n,m,prim[20];
int calc(){ //容斥原理 集合的并
int res=0;
for(int i=1;i<1<<m;i++){
int t=1,sign=-1;
for(int j=0;j<m;j++){
if(i&(1<<j)){
if((ll)t*prim[j]>n) {
t=0;break;
}
t=t*prim[j];
sign=-sign; //奇正偶负
}
}
if(t) res+=n/t*sign;
}
return res;
}
int main(){
cin>>n>>m;
for(int i=0;i<m;i++) cin>>prim[i];
cout<<calc()<<endl;
}
2、集合的交


#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long ll;
ll c[4],f[100005],d[4];
int s,n;
//容斥原理:集合的交=全集-补集的并
void js(){
f[0]=1;
for(int i=0;i<4;i++){
for(int j=c[i];j<=100004;j++) f[j]+=f[j-c[i]];
}
}
ll cal(){
ll res=0;
//计算补集的并
for(int i=1;i<1<<4;i++){
ll t=0,sign=-1;
for(int j=0;j<4;j++){
if(i&(1<<j)){ //这个结构和集合的并相似
t+=c[j]*(d[j]+1);
sign=-sign;
}
}
if(s>=t) res+=f[s-t]*sign;
}
return f[s]-res;//全集-补集的并
}
int main(){
for(int i=0;i<4;i++) scanf("%d ",&c[i]);
scanf("%d",&n);
js();
while(n--){
for(int i=0;i<4;i++) scanf("%d ",&d[i]);
scanf("%d",&s);
printf("%lld\n",cal());
}
}
6、 Fibonacci数列
应用:楼梯问题、矩形覆盖问题
n<=10^6 用公式即可
若数更大了,需要用到矩阵快速幂,把递推关系转化为矩阵
例:求Fibonacci第n项
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=1010;
const int INF=0x3fffffff;
typedef long long LL;
typedef unsigned long long ull;
//这个是模板
//斐波那契数列取模
/*
(1)
1 0 * 1 1 = 1 1
1 0
(2)
1 1 * 1 1 = 2 1
1 0
(3)
2 1 * 1 1 = 3 2
1 0
所以第n项就是1 0 * (1,1)^n
(1,0)
用快速幂优化就是矩阵快速幂了
*/
LL n,mod;
LL a[3][3],b[3][3],ans[3][3],c[3][3];
void add(LL &x,LL y){
x=x+y;
x-=(x>=mod)?mod:0;
return;
}
// memmove用于拷贝字节,如果目标区域和源区域有重叠的话,memmove能够保证源串在被覆盖之前将重叠区域的字节拷贝到目标区域中,但复制后源内容会被更改。
//但是当目标区域与源区域没有重叠则和memcpy函数功能相同。
int main(){
scanf("%lld %lld",&n,&mod);
n-=1;
a[1][1]=a[1][2]=a[2][1]=1;a[2][2]=0;
ans[1][1]=ans[2][2]=1;ans[2][1]=ans[1][2]=0;
while(n){
if(n&1){ //快速幂
memset(c,0,sizeof(c));
for(int i=1;i<=2;i++){
for(int j=1;j<=2;j++){
for(int k=1;k<=2;k++) add(c[i][j],ans[i][k]*a[k][j]%mod);
}
}
memmove(ans,c,sizeof(ans)); //这个函数是实现字节的拷贝
}
memset(c,0,sizeof(c));
//对a进行倍乘
for(int i=1;i<=2;i++)
for(int j=1;j<=2;j++){
for(int k=1;k<=2;k++) add(c[i][j],a[i][k]*a[k][j]%mod);
}
memmove(a,c,sizeof(a));
n>>=1;
}
b[1][1]=1;b[1][2]=0;
memset(c,0,sizeof(c));
for(int i=1;i<=1;i++){
for(int j=1;j<=2;j++){
for(int k=1;k<=2;k++) add(c[i][j],ans[i][k]*b[k][j]);
}
}
memmove(b,c,sizeof(b));
printf("%lld\n",b[1][1]);
return 0;
}
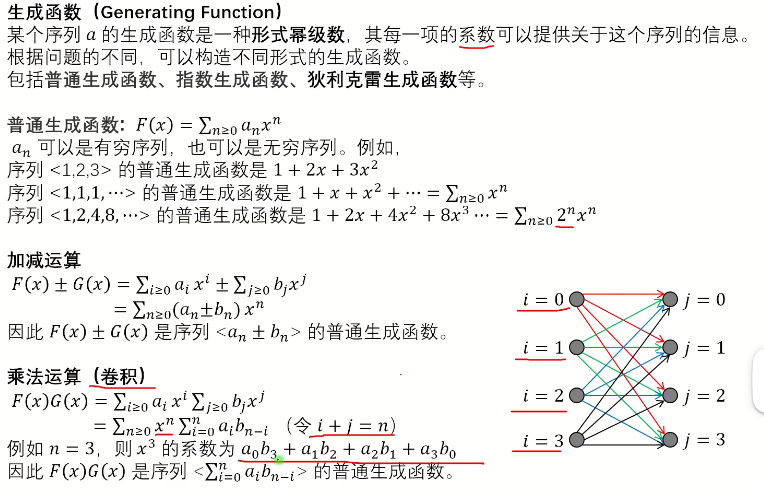
7、母函数
用代数方法解决组合计数问题
整数划分问题(把一个整数划分为多个整数的和,这些数大于1,小于等于n),详解:https://www.cnblogs.com/radiumlrb/p/5797168.html
解决方法:递归、DP、母函数(how:把组合问题的加法与幂级数的幂乘对应起来)
母函数:
(x^(0*1)+x^(1*1)+x(2*1)+....)*(x^(0*2)+x^(1*2)+x^(2*2)+...)*(x^(0*3)+x^(1*3)+x^(2*3)+....)..
=(1+x+x^2+...)*(1+x^2+x^4+...)*(1+x^3+x^6)....
分别表示不用数字1,用1次,用2次...
普通型母函数---求组合方案数
//母函数求整数划分
int c1[maxn],c2[maxn];
void part(){
for(int i=0;i<=maxn;i++){ //初始化,第一部分(1+x+x^2+...)的系数,都是1
c1[i]=1;c2[i]=0;
}
for(int k=2;k<=maxn;k++) { //从第二部分(1+x^2+x^4+..)开始展开
for(int i=0;i<=maxn;i++){
//k=2是,i循环第一部分(1+x+x^2+...),j循环第二部分 (1+x^2+x^4+..)
for(int j=0;j+i<=maxn;j+=k){
c2[i+j]+=c1[i];
}
for(int i=0;i<=maxn;i++){
c1[i]=c2[i];
c2[i]=0;
}
}
}
//c1[n]用来记录每次展开后第x^n项的系数,结束后,c1[n]就是整数n的划分数
}

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long ll;
//普通生成函数、
int n,m;
int a[110],b[110]; //寸幂次
int c[110],d[110]; //寸系数
int calc(){
for(int i=0;i<=m;i++) c[i]=d[i]=0;
for(int i=a[1];i<=b[1];i++) c[i]=1;
for(int i=2;i<=n;i++){
//计算x^(j+k)的系数
for(int j=0;j<=m;j++){
for(int k=a[i];k<=b[i];k++) d[j+k]+=c[j];
}
for(int j=0;j<=m;j++) c[j]=d[j],d[j]=0;
}
return c[m];
}
int main(){
while(~scanf("%d %d",&n,&m)){
for(int i=1;i<=n;i++) scanf("%d %d",&a[i],&b[i]);
printf("%d\n",calc());
}
}
HDU - 1085 Holding Bin-Laden Captive!
注意一下要切换思路:把指数跟数值联系起来,这样系数才有意义,还有循环时范围的设置
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long ll;
//普通生成函数、
int a[4],b[4],c[8005],d[8005],n;
void calc(int m){
for(int i=0;i<=m;i++) c[i]=d[i]=0;
for(int i=0;i<=a[1];i++) c[i]=1;
for(int i=2;i<=3;i++){
for(int j=0;j<=m;j++){
for(int k=0;k<=a[i]*b[i]&&j+k<=m;k+=b[i]){ //注意这里需要改变 ,不超过最大值而且不会越界
d[j+k]+=c[j];
}
}
for(int j=0;j<=m;j++) c[j]=d[j],d[j]=0;
}
}
int main(){
while(scanf("%d%d%d",&a[1],&a[2],&a[3])&&(a[1]||a[2]||a[3])){
b[1]=1;
b[2]=2;
b[3]=5; //价格
int m=a[1]*b[1]+a[2]*b[2]+a[3]*b[3]; //最大值
calc(m);
int x=1;
while(x<=m&&c[x]) x++; //找到第一个幂次为0的
printf("%d\n",x);
}
return 0;
}
指数型母函数----求排序数


例如:hdu 1521 排序组合------指数型母函数
k个物品的排列和k个物品的组合相差k!倍
指数阶一般求解的问题:已知有n种颜色的球,第1种X1个,第2种X2个,第3种X3个。。。求从中取m个的方案数(排列数)。
公式中的ak/k!就是所求的组合数,ak为排列数。
只要把求系数的时候每个都相应的 除以i的阶乘即可
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=1010;
const int INF=0x3fffffff;
typedef long long LL;
typedef unsigned long long ull;
//指数型母函数
/*
指数型母函数
指数阶一般求解的问题:已知有n种颜色的球,第1种X1个,第2种X2个,第3种X3个。。。求从中取m个的方案数(组合数)。
公式中的ak/k!就是所求的组合数,ak为排列数。
只要把求系数的时候每个都相应的 除以i的阶乘即可
另一种方法:https://blog.csdn.net/a601025382s/article/details/10274259
*/
int a[21],c[11];
int n,m;
int main(){
c[0]=1;
for(int i=1;i<=10;i++) c[i]=c[i-1]*i;
double c1[21],c2[21];
while(~scanf("%d %d",&n,&m)){
memset(c1,0,sizeof(c1));
memset(c2,0,sizeof(c2));
for(int i=1;i<=n;i++) scanf("%d",&a[i]); //个数
c1[0]=1.0;
for(int i=1;i<=n;i++){
for(int j=0;j<=m;j++)
for(int k=0;k+j<=m&&k<=a[i];k++)
c2[j+k]+=c1[j]/c[k];
for(int j=0;j<=m;j++){
c1[j]=c2[j];
c2[j]=0;
}
}
printf("%.0f\n",c1[m]*c[m]);
}
return 0;
}
另一种方法:https://blog.csdn.net/a601025382s/article/details/10274259
有n种物品,每种取ai种(∑ai==m),则方案数有
ans=m!/(a1!*a2!*...an!)=m!/(a1!*(m-a1)!)*(m-a1)!/(a2!*(m-a1-a2)!)...=c(m,a1)*c(m-a1,a2)*...
含义就是第一种物品有a1个,由于相同,所以就是在m个位置上选a1个,共c(m,a1)种放法,剩下m-a1个位置,
再第二种物品有a2个,再在m-a1个位置选a2个放,有c(m-a1,a2)。。。以此类推就是方案数了。。
然后用变形的背包或则说dp..来解,
f[i]表示已经选好了i件的排列数。。应该这么叫吧,如果没有排列这个就是方案数了。
这里的好处就是(a+b)*c=a*c+b*c;原本应该独立处理每种{ai}序列,最后加上排列数,但这种耗时太大,不能用。
所以就要压缩时间,对于队列两个序列{ai},{bi},如果a1+a2=b1+b2=p,a3=b3=q,;则c(m,a1)*c(m-a1,a2)*c(m-a1-a2,a3)+
c(m,b1)*c(m-b1,b2)*c(m-b1-b2,b3)=(c(m,a1)*c(m-a1,a2)+c(m,b1)*c(m-b1,b2))*c(m-p,q);
这就解释了,为什么上面不用求出每个方案,然后求排列了。。
#include <cstdio>
#include <cmath>
#include <cstring>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
int c[11][11];//组合数
int f[11],a[11];
void init()
{
int i,j;
memset(c,0,sizeof(c));
c[1][0]=c[1][1]=1;
for(i=2;i<=10;i++)
{
c[i][0]=c[i][i]=1;
for(j=1;j<i;j++)
c[i][j]=c[i-1][j]+c[i-1][j-1];
}
}
int main()
{
init();
int n,m;
while(cin>>n>>m)
{
int i,j,k;
for(i=0;i<n;i++)
cin>>a[i];
memset(f,0,sizeof(f));
f[0]=1;
for(i=0;i<n;i++)
{
for(j=m;j>=0;j--)//枚举已经选择了j件物品
{
for(k=1;k<=min(a[i],m-j);k++)//k不能为0不然就会加上本身
f[k+j]+=c[m-j][k]*f[j]; //每次都只处理用f[j]处理f[j+k],j+k>j,使得不会因为前面处理影响后面的处理
}
}
cout<<f[m]<<endl;
}
return 0;
}

8、特殊计数
(1) Catalan数
http://www.cppblog.com/MiYu/archive/2010/08/07/122573.html
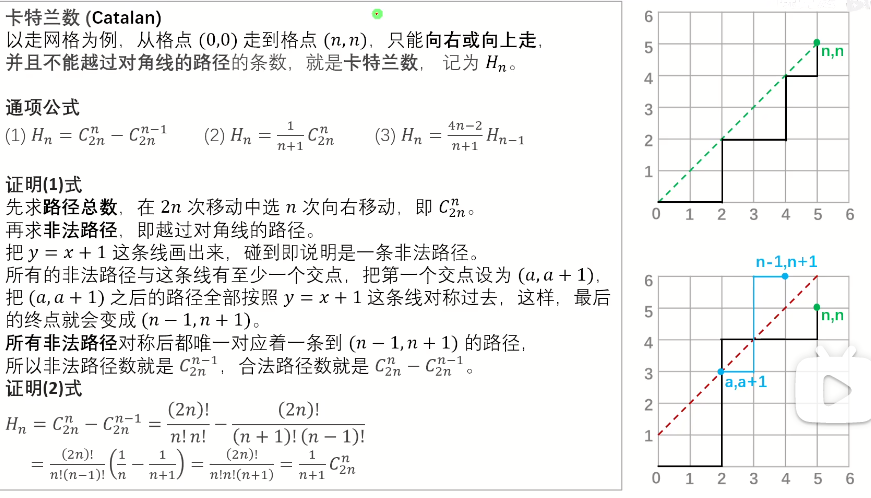
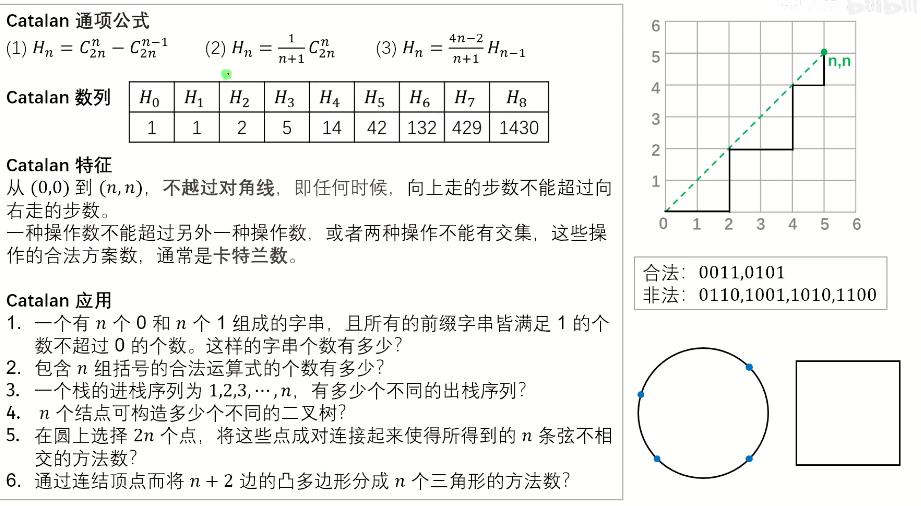
很重要的一个特征:一种操作数不能超过另外一种操作数,或者两种操作不能有交集,求这些操作的合法方案。
Hn=1/(n+1)*C(2n,n) Hn=C(2n,n)-C(2n,n-1) Hn=(4n-2)/(n+1)Hn-1
是许多组合计数问题的数学模型,是一个很常见的数列
模型1:Cn=1/(n+1)C(2n,n)=C(2n,n)-C(2n,n+1)=C(2n,n)-C(2n,n-1)
C(2n,n+1)与C(2n,n-1)等价
推导:把n个1和n个0排成一行,使这一行前k个数中1的数量总是大于或者等于0的数量(0>=1等价),排列有多少个?一共有Cn个,即Catalan数
模型2:递推
Cn=C0Cn-1+C1Cn-2+...+Cn-2C1+Cn-1C0, C0=1
应用场景:
(1)棋盘问题
例如:hdu 2067
小兔的叔叔从外面旅游回来给她带来了一个礼物,小兔高兴地跑回自己的房间,拆开一看是一个棋盘,小兔有所失望。不过没过几天发现了棋盘的好玩之处。从起点(0,0)走到终点(n,n)的最短路径数是C(2n,n),现在小兔又想如果不穿越对角线(但可接触对角线上的格点),这样的路径数有多少?小兔想了很长时间都没想出来,现在想请你帮助小兔解决这个问题,对于你来说应该不难吧!
意思:从左下角走到右上角,一直在对角线右下方走,不穿过主对角线,有多少种走法? -----模型1
对方向编号,向右是0,向上是1,在前k步中,0数量大于1数量,

两种写法都可以(第二种没看懂)
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=1010;
const int INF=0x3fffffff;
typedef long long LL;
typedef unsigned long long ull;
/*按照正常思路来求解:https://www.cnblogs.com/liudehao/p/4113876.html
一定要看明白那个图!
观察上图你就可以发现,其实这是一张关于对角线对称的图。所有我们只要求一个方向的值,然后乘以2即可。
我们就拿下三角来考虑。不难发现,所有在0列上的格子,路径数都是 1 (只能从上面过来)。
而其他格子则都是由上、左两个方向过来,即:f(i, j) = f(i - 1, j) + f(i, j - 1);
另外f(i, i) = f(i, j - 1) 或者 f(i, i) = f( i-1, j ) ;
LL f[40][40];
int cases=0;
int main(){
int n;
while(scanf("%d",&n)!=EOF){
++cases;
if(n==-1) break;
for(int i=1;i<=n;i++) f[0][i]=1;
for(int i=1;i<n;i++){
for(int j=i;j<=n;j++){
if(i==j) f[i][j]=f[i-1][j];
else f[i][j]=f[i-1][j]+f[i][j-1];
}
}
printf("%d %d %lld\n",cases,n,2*f[n-1][n]);
}
return 0;
}
*/
/*卡特兰数求法
令h(1)=1,h(0)=1,catalan数满足递归式:
h(n)= h(0)*h(n-1)+h(1)*h(n-2) + + h(n-1)h(0) (其中n>=2)
另类递归式:
h(n)=((4*n-2)/(n+1))*h(n-1);
该递推关系的解为:
h(n)=C(2n,n)/(n+1) (n=1,2,3,…)
*/
int main(){
LL a[40][40];
a[0][0]=0;a[0][1]=1;a[1][1]=2;
for(int i=2;i<37;i++){
a[i][0]=1;
for(int j=1;j<i-1;j++) a[i][j]=a[i][j-1]+a[i-1][j];
a[i][i-1]=a[i][i-2]+a[i-1][i-1]/2;
a[i][i]=2*a[i][i-2]+a[i-1][i-1];
}
int n,cases=0;
while(scanf("%d",&n)!=EOF){
++cases;
if(n==-1) break;
printf("%d %d %lld\n",cases,n,a[n][n]);
}
return 0;
}
(2)括号问题
n个(和n个)组成字符串,有多少合法的组合,合法的组合是:任意前k个括号组合,左括号的数量大于等于有括号的数量
--->模型1
hdu 5184
(3)出栈序列问题
给定一个入栈序列,求出多少字可能的出栈序列,合法的序列:对应每一个数字,在它后面的比它小的所有数字一定是按照递减序列排列的
定义进栈为0,出栈为1,那么出栈序列要求进栈的操作数大于等于出栈的操作数,n个0和n个1
hud 1023
(4)二叉树问题
n个节点构成的二叉树有多少种情况?
模型2(左边多少个节点,右边多少个节点。。。。)
(5)其他问题
eg.买票找零、三角剖分(凸多边形内部划分为多个三角形有多少种方法)
求法:
卡特兰数求法
令h(1)=1,h(0)=1,catalan数满足递归式:
法1:h(n)= h(0)*h(n-1)+h(1)*h(n-2) + + h(n-1)h(0) (其中n>=2)
法2:h(n)=((4*n-2)/(n+1))*h(n-1);
法3:h(n)=C(2n,n)/(n+1) =2n!/(n+1)!n! (n=1,2,3,…)
法1对应的n较小,n<=100,对于(2)(3)的应用:n很大,不能直接输出,而是要做取模操作
但是2、3都有大数除法,会损失精度,所以需要转化为逆元,然后取模
(2)第二类Stirling数
第一类Stirling数:仓库钥匙问题
把n个仓库分配到k个圆里,不能有空的圆,有多少种分法:第一类Stirling数 (大一些)
s(n,k)=s(n-1,k-1)+(n-1)*s(n-1,k)
s(0,0)=1
s(k,0)=0
第二类Stirling数:s(n,k):把n个不同的球分配到k个相同的盒子里,不能有空,有多少种分法?
s(n,k)=k*s(n-1,k)+s(n-1,k-1)
s(0,0)=1
s(i,0)=0


 posted on
posted on

 浙公网安备 33010602011771号
浙公网安备 33010602011771号