题目一般要求由前面的一个状态得出当前的最优状态,满足dp,但如果暴力查找前一个决策,复杂度显然不可以接受。这时候可以用一个能从两端删除但只能从一段添加的单调队列及时把不可能的决策排除掉,然后再把当前的决策插进去,保持队列中的单调性。
学习资源:
在每次操作时,要维护一个区间(范围)内的数据,例如总和,最大最小值等等,在每次的操作时可以直接取这个最值
单调队列维护最小或者最大。典型题就是滑动窗口,要控制窗口的大小,通过head++,也要维护窗口的单调性,通过tail--
1、求定长区间最大最小值、和极值
1597:【 例 1】滑动窗口
很裸的一道题,总大小为n,窗口大小为k,求每次看到的最大、最小值
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=1e6+10;
const int INF=0x3fffffff;
typedef long long LL;
int a[maxn];
int n,k;
//第一次试了暴力,果然是滴,一半以上的点都过不了
//看了题解,单调队列,窗口,对我来说最需要理解的是: 维护队列的大小,也就是保证队列的大小为窗口值
int minn[maxn],maxx[maxn];
int num[maxn],pos[maxn];
//表示对应的值,值所在的位置
void dp_min(){
int head=1,tail=0;//head>tail表示空队列
for(int i=1;i<=n;i++){
while(pos[head]<i-k+1&&head<=tail) head++;//将队列维持好数量
while(a[i]<=num[tail]&&head<=tail) tail--;//把不可能最小的弹出队列
num[++tail]=a[i]; //加入队列
pos[tail]=i;//记录元素编号
minn[i]=num[head];//队首元素一定是最小的
}
}
void dp_max(){
int head=1,tail=0;
for(int i=1;i<=n;i++){
while(pos[head]<i-k+1&&head<=tail) head++;
while(a[i]>=num[tail]&&head<=tail) tail--;
num[++tail]=a[i];
pos[tail]=i;
maxx[i]=num[head];
}
}
int main(){
scanf("%d %d",&n,&k);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
dp_min();
dp_max();
for(int i=k;i<=n;i++) printf("%d ",minn[i]);
printf("\n");
for(int i=k;i<=n;i++) printf("%d ",maxx[i]);
return 0;
}
1598:【 例 2】最大连续和
一个大小为n的序列,求不超过m大小的连续子序列和
维护一个前缀和,队列里面是前缀和,枚举右端点也就是i,然后单调队列的范围就是i-m~i-1
在单调队列里面是从小到大排的,然后找到里面最小的前缀和,其实也就是Head
然后用现在的pre[i+1]-pre[pos[head]]就可以得到了
(我们需要维护一个i-k ~ i+1的区间(长度为m),找到一个最小的前缀和(这样就可以保证这个区间内的和最大),用pre[i+1]-这个前缀和就是这个区间的最大值了,那么用ans来记录一下最大值即可。)
同时有一个细节:看到别人的博客都有这样一句话if(n<=m) ans=max(ans,pre[n]);,这是为什么呢?当n=4,k=6时,数字分别是1,1,1,1,这种情况应该输出4,但是程序会输出3,这是为什么呢?因为队列一定不会是空的,也就是说一定会减去1,那么答案就错了
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=2e5+10;
const int INF=0x3fffffff;
typedef long long LL;
//想了半天 没想通
//结果一看题目 昏过去
//不超过m的最大子序列和
///维护一个前缀和,枚举右端点也就是i,然后单调队列的范围就是i-m~i-1
//在单调队列里面是从小到大排的,然后找到里面最小的前缀和,其实也就是Head
//然后用现在的pre[i+1]-pre[pos[head]]就可以得到了
//同时还有一个细节要注意
/*
我们需要维护一个i-k ~ i+1的区间(长度为m),找到一个最小的前缀和(这样就可以保证这个区间内的和最大),用pre[i+1]-这个前缀和就是这个区间的最大值了,
那么用ans来记录一下最大值即可。
同时要注意一个细节:看到别人的博客都有这样一句话if(n<=m) ans=max(ans,pre[n]);,这是为什么呢?当n=4,k=6时,数字分别是1,1,1,1,这种情况应该输出4,但是程序会输出3,
这是为什么呢?因为队列一定不会是空的,也就是说一定会减去1,那么答案就错了。
*/
int n,m;
int pre[maxn],pos[maxn];
int ans;
void dp(){
int head=1,tail=0;
ans=pre[1];
//注意
if(n<=m) ans=max(ans,pre[n]);
for(int i=1;i<n;i++){
while(pos[head]<i-m+1&&head<tail) head++; //维护队列大小
while(pre[pos[tail]]>=pre[i]&&head<=tail) tail--; //取最小
pos[++tail]=i;
ans=max(ans,pre[i+1]-pre[pos[head]]);
}
}
int main(){
scanf("%d %d",&n,&m);
int x;
for(int i=1;i<=n;i++){
scanf("%d",&x);
pre[i]=pre[i-1]+x;
}
dp();
printf("%d",ans);
return 0;
}
2、在动态规划里面的运用(优化计算速度)
1599:【 例 3】修剪草坪
n只奶牛,不许选择不会连续超过k只奶牛的组合,求最大组合值
单调队列是在DP中的优化,你要重视这一点
用pre[i]表示前缀和
考虑dp[i][0,1]表示到第i个牛(是否工作)的最大效率和
dp[i][0]=max(dp[i-1][0],dp[i-1][1]) i不会工作
dp[i][1]=max(dp[x][0]+pre[i]-pre[x]);(i-m≤x<i) i工作,
dp[i][1]可以用单调队列优化,维护队首为dp[i][0]-S[i]最大的单调队列
因为你看上面的转移表达式,dp[x][0]-pre[x]这个是相关的,可以控制的,所以把这个作为控制单调队列的值
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=1e5+10;
const int INF=0x3fffffff;
typedef long long LL;
//单调队列是在DP中的优化,你要重视这一点,
int n,m,qu[maxn]; //队列,其实存的是下标
LL pre[maxn];
LL dp[maxn][2];
/*
用pre[i]表示前缀和
考虑dp[i][0,1]表示到第i个牛(是否工作)的最大效率和
dp[i][0]=max(dp[i-1][0],dp[i-1][1])
dp[i][1]=max(dp[x][0]+pre[i]-pre[x]);(i-m≤x<i)
dp[i][1]可以用单调队列优化,维护队首为dp[i][0]-S[i]最大的单调队列
//因为你看上面的转移表达式,dp[x][0]-pre[x]这个是相关的,可以控制的,所以把这个作为控制单调队列的值
*/
void dpp(){
int head=1,tail=1;
qu[head]=0;
for(int i=1;i<=n;i++){
dp[i][0]=max(dp[i-1][0],dp[i-1][1]); //不选
while(head<tail&&qu[head]<i-m) head++;
dp[i][1]=dp[qu[head]][0]+pre[i]-pre[qu[head]]; //选
while(head<=tail&&(dp[i][0]-pre[i])>(dp[qu[tail]][0]-pre[qu[tail]])) tail--; //退出
//保持最大
qu[++tail]=i;
}
}
int main(){
scanf("%d %d",&n,&m);
LL x;
for(int i=1;i<=n;i++){
scanf("%lld",&x);
pre[i]=pre[i-1]+x;
}
dpp();
printf("%lld",max(dp[n][1],dp[n][0]));
return 0;
}
3、在非dp里面的运用
1600:【例 4】旅行问题

能不能走通这个问题--如何表示
就是可以用油钱和路费相减,看是不是负数
若一个点是不能环绕一圈的,那么就是这个点在绕一圈过程中油量的最小值<0,每个点对当前油的贡献就是pi-di,这样就可以维护出一个前缀和,
(断环成链后长度为2n),i点是否合法就是判断(S[i]~S[i+n-1]中的最小值-S[i])是否小于0,小于0就不可以,逆时针一模一样搞一遍,就是pi和di会变一下
也有环形DP的思想噢
出现了!!!可以用struct表示,一个表示值,一个表示下标
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=2e6+10;
const int INF=0x3fffffff;
typedef long long LL;
//真的觉得,有很多编程思路,我是很欠缺的
//比如能不能走通这个问题--如何表示
//就是可以用油钱和路费相减,看是不是负数---》这就是我欠缺的编程思路,或者是灵感
/*
若一个点是不能环绕一圈的,那么就是这个点在绕一圈过程中油量的最小值<0,每个点对当前油的贡献就是pi-di,这样就可以维护出一个前缀和,
(断环成链后长度为2n),i点是否合法就是判断(S[i]~S[i+n-1]中的最小值-S[i])是否小于0,小于0就不可以,逆时针一模一样搞一遍,就是pi和di会变一下
*/
struct node{
LL c; //值
int x; //位置
}la[maxn],lb[maxn];
//分别维护顺时针、逆时针 的队列
LL disa[maxn],gasa[maxn];
LL a[maxn],b[maxn];
//顺时针、逆时针的前缀和
bool ans[maxn];
//判断能不能走一圈,顺逆时针一起判断
int n;
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%lld %lld",&gasa[i],&disa[i]);
gasa[i+n]=gasa[i];
disa[i+n]=disa[i];
}
for(int i=1;i<=2*n;i++){ //断环成链
a[i]=gasa[i]-disa[i]+a[i-1];
b[i]=gasa[2*n-i+1]-disa[2*n-i]+b[i-1];//理解这个逆时针
}
//维护单调递增的队列,找到最小值
//区间大小为n
//看当前的最小值-自己>=0 这样的区间内没有负数,也就是可以走完
int heada=1,headb=1,taila=0,tailb=0;
la[1].c=0;la[1].x=0;
lb[1].c=0;lb[1].x=0;
for(int i=1;i<=2*n;i++){
while(heada<=taila&&la[heada].x<i-n) heada++; //区间大小
while(heada<=taila&&a[i]<=la[taila].c) taila--; //维持递增
la[++taila].c=a[i];
la[taila].x=i;
while(headb<=tailb&&lb[headb].x<i-n) headb++;
while(headb<=tailb&&b[i]<=lb[tailb].c) tailb--;
lb[++tailb].c=b[i];
lb[tailb].x=i;
if(i>n){
if(la[heada].c-a[i-n-1]>=0) ans[i-n]=1;
if(lb[headb].c-b[i-n-1]>=0) ans[2*n-i+1]=1;
}
}
for(int i=1;i<=n;i++){
if(ans[i]) printf("TAK\n");
else printf("NIE\n");
}
return 0;
}
4、在多重背包中的运用(还有二进制优化)
1601:【例 5】Banknotes
这道题属于:单调队列优化多重背包)
董老师讲得很清楚,把体积V拿来拆分,按照余数拆分为V个
调队列优化:对于模Bi相同的几个权值之间的dp转移,可以用单调队列优化,令权值V=j+k*Bi,dp[V]=min(dp[V],dp[j+k'*Bi]+k-k‘),
所以可以用dp[j+k*Bi]-k最小为队首的单调队列来优化成n*m,(细节:为了防止被反复统计,应该先插入当前节点再更新当前节点的dp值)
现在枚举到第i种硬币,面值bi,个数ci。回顾上面的状态转移方程,发现f[j]和f[j-bi*k]的关联不大,这里就把所有要凑的面值x按照对bi取模的结果分租。
假设取模余d。那么bi*0+d,bi*1+d,bi*2+d....bi*j+d,都是一组的。假设x=bi*j+d,那么满足下面的关系:
f[x] = f[bi*j+d] = min{ f[bi*k+d] + (j-k) }。 其中,j-k<=ci。
也许细心的大佬会觉得应该是 j<=ci,否则万一k和j都取到了,可能会大于c[i]。确实,在上面的代码里,j倒着枚举就是考虑到了这种情况(正着枚举是数量无限的情况)。不过下面在进队时的细节可以避免它。
转化一下: f[bi*j+d] = min{ f[bi*k+d] - k } + j (j-k<=ci) 。
如果把 bi*0+d~bi*k+d 都入队,那么就转变成了在一个队列里求最小值,可以用单调队列解决。
入队的细节:上面的代码倒着枚举是因为要用到未更新时的数据。类似地,我们也在更新前把f[bi*j+d]入队,再对它更新。
最后更新就是:if(q[L].num+j<dp[x]) dp[x]=q[L].num+j
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=210;
const int N=2e4+10;
const int INF=0x3fffffff;
typedef long long LL;
int n,m;
int val[maxn],num[maxn];
LL dp[N];
//单调队列优化多重背包)
/*
单调队列优化:对于模Bi相同的几个权值之间的dp转移,可以用单调队列优化,令权值V=j+k*Bi,dp[V]=min(dp[V],dp[j+k'*Bi]+k-k‘),
所以可以用dp[j+k*Bi]-k最小为队首的单调队列来优化成n*m,(细节:为了防止被反复统计,应该先插入当前节点再更新当前节点的dp值)
*/
//还是有点难理解
struct node{
int k; //当前的个数
int num; //dp[j+k*Bi]-k当前的值
};
node q[N];
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",&val[i]);
}
for(int i=1;i<=n;i++){
scanf("%d",&num[i]);
}
scanf("%d",&m);
//一般来说多重背包的写法,但是这样会超时
/*
for(int i=1;i<=k;i++) dp[i]=INF;
dp[0]=0;
for(int i=1;i<=n;i++){
for(int j=k;j>=val[i];j--){
for(int z=1;z<=min(num[i],j/val[i]);z++){
dp[j]=min(dp[j],dp[j-z*val[i]]+z);
}
}
}
*/
/*
for(int i=1;i<=n;i++){
for(int j=1;j<=num[i];j++){
for(int z=k;z>=val[i];z--){
dp[z]=min(dp[z],dp[z-val[i]]+1);
}
}
}
*/
memset(dp,0x3f,sizeof(dp));
dp[0]=0;
int x;
for(int i=1;i<=n;i++){//枚举第i种硬币
for(int d=0;d<val[i];d++){ //枚举除以该硬币面额的余数
int L=1,R=0; //维护一个队首元素(num) 最小的队列
for(int j=0;;j++){ // x=b[i]*j + d ,枚举j
x=j*val[i]+d; //此时的总金额
if(x>m) break;
while(L<=R&&j-q[L].k>num[i]) L++; // //判断是否超过c[i]
//个数-队首的个数
while(L<=R&&dp[x]-j<=q[R].num) R--; //判断是否满足单调
q[++R]=node{j,dp[x]-j}; //更新前入队
if(q[L].num+j<dp[x]) dp[x]=q[L].num+j; //更新
}
}
}
printf("%lld\n",dp[m]);
return 0;
}
1602:烽火传递
大小为n的序列,每连续m的数字之间至少有一个被选中,求最小选中代价
dp[i]表示强制选i这个位置时1~i的最小代价,dp[i]=min(dp[i-m]~dp[i-1])+ a[i]
min(dp[i-m]~dp[i-1])可以方便的用单调队列优化,所以复杂度就变成O(n)了
答案就是min(dp[n-m+1]~dp[n])
这道题也算是裸题
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=2e5+19;
const int INF=0x3fffffff;
typedef long long LL;
//这个写法我更好理解
//另一种写法
int q[maxn];
int a[maxn];
int dp[maxn];
int n,m;
int main(){
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
int head=1,tail=1;
for(int i=1;i<=n;i++){
dp[i]=dp[q[head]]+a[i];
while(head<=tail&&dp[i]<=dp[q[tail]]) tail--;
q[++tail]=i;
while(q[head]<i-m+1) head++;
}
printf("%d",dp[q[head]]);
return 0;
}
1603:绿色通道

是我欠缺的思维,。。。呜呜呜呜
给定了限定的时间,在这段时间以内,必须在连着的m(答案)题里面做一道
因为要m最小,并且最后这些题用的时间加起来不超过限定的时间,所以我们可以枚举二分!!!k呀
看在连续的k个数里面至少取一个会不会超过时间t
(设k为最长的空题数,问题转换为每k+1个数字至少要取一个数,取出的数字之和小于等于t,二分枚举k即可)
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=5e4+10;
const int INF=0x3fffffff;
typedef long long LL;
//又是我欠缺的思维,。。。呜呜呜呜
//给定了限定的时间,在这段时间以内,必须在连着的m(答案)题里面做一道
//因为要m最小,并且最后这些题用的时间加起来不超过限定的时间,所以我们可以枚举二分!!!k呀
//看在连续的k个数里面至少取一个会不会超过时间t
/*
设k为最长的空题数
问题转换为每k+1个数字至少要取一个数,取出的数字之和小于等于t
二分枚举k即可
*/
int n,t;
int a[maxn],dp[maxn];
struct node{
int x,c;
//分别是位置、总和
}q[maxn];
bool check(int m){ //看上面,
memset(dp,0x3f,sizeof(dp));
dp[0]=0;
int head=1,tail=1;
q[1].x=0;q[1].c=0;
for(int i=1;i<=n;i++){
while(head<=tail&&q[head].x<i-m) head++;
dp[i]=q[head].c+a[i];
while(head<=tail&&q[tail].c>dp[i]) tail--;
q[++tail].c=dp[i];
q[tail].x=i;
}
return dp[n]<=t;
}
int main(){
scanf("%d %d",&n,&t);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
int l=0,r=n,ans=0; //二分这个“间隔”ans记录答案
a[++n]=0;
while(l<=r){
int mid=(l+r)/2;
if(check(mid)) {
r=mid-1;ans=r;
}
else l=mid+1;
}
printf("%d",ans);
return 0;
}
1604:理想的正方形
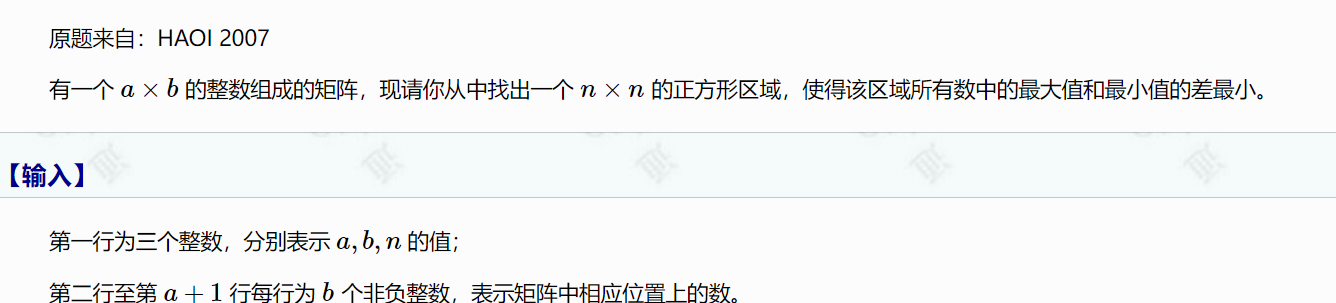
其实思路不难,直接又简便,只需要用数列表示某一个区间的最值
二维单调队列:先处理出Min[i][j][0]表示以(i,j)为右下角的长度为n的一整条中的最小值,用单调队列a*b就可以处理出来了
再用Min[i][j][0]到列上去跑单调队列,得到Min[i][j][1]表示以(i,j)为右下角的一个n*n的正方形中的最小值
也可以用二维ST表做,忘了but
一本通1604理想的正方形 - 人间不值の - 博客园 (cnblogs.com)
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
using namespace std;
typedef long long LL;
const int maxn=1000+10;
const int INF=0x3f3f3f3f;
int a,b,n;
int val[maxn][maxn];
int maxx[maxn][maxn][2],minn[maxn][maxn][2];
// [i][j][0]表示的是以(i,j)为右下角的横着的最小值(最大值)
// [i][j][1]表示的是以(i,j)为右下角的n*n正方形(最大值)
struct node{
int zhi; //最值
int pos; //位置
}q[maxn];
int main(){
scanf("%d %d %d",&a,&b,&n);
for(int i=1;i<=a;i++){
for(int j=1;j<=b;j++) scanf("%d",&val[i][j]);
}
int head,tail;
//横着的
for(int i=1;i<=a;i++){
head=1;tail=0;
for(int j=1;j<=b;j++){
while(head<=tail&&val[i][j]<q[tail].zhi) tail--;
q[++tail].pos=j;q[tail].zhi=val[i][j];
while(head<=tail&&q[head].pos<j-n+1) head++;
minn[i][j][0]=q[head].zhi;
}
head=1;tail=0;
for(int j=1;j<=b;j++){
while(head<=tail&&val[i][j]>q[tail].zhi) tail--;
q[++tail].pos=j;q[tail].zhi=val[i][j];
while(head<=tail&&q[head].pos<j-n+1) head++;
maxx[i][j][0]=q[head].zhi;
}
}
//正方形了
for(int j=n;j<=b;j++){
head=1;tail=0;
for(int i=1;i<=a;i++){
while(head<=tail&&minn[i][j][0]<q[tail].zhi) tail--;
q[++tail].pos=i;q[tail].zhi=minn[i][j][0];
while(head<=tail&&q[head].pos<i-n+1) head++;
minn[i][j][1]=q[head].zhi;
}
head=1;tail=0;
for(int i=1;i<=a;i++){
while(head<=tail&&maxx[i][j][0]>q[tail].zhi) tail--;
q[++tail].pos=i;q[tail].zhi=maxx[i][j][0];
while(head<=tail&&q[head].pos<i-n+1) head++;
maxx[i][j][1]=q[head].zhi;
}
}
int ans=INF;
for(int i=n;i<=a;i++){
for(int j=n;j<=b;j++){
ans=min(ans,maxx[i][j][1]-minn[i][j][1]);
}
}
printf("%d\n",ans);
return 0;
}
1605:股票交易
http://t.zoukankan.com/gaojunonly1-p-10381300.html
这道题的状态转移有额外添加一个转移状态k 前面有道题也是这样
数据范围与提示:
对于 30% 的数据,0≤W<T≤50,1≤MaxP≤50;
对于 50% 的数据,0≤W<T≤2000,1≤MaxP≤50;
对于 100% 的数据,0≤W<T≤2000,1≤MaxP≤2000,1≤BPi?≤APi?≤1000,1≤ASi?,BSi?≤MaxP。
sol:一本通居然没有数据范围太优秀了
很容易发现可以dp,dp[i][j]表示到第i个位置,有j张股票最多赚多少钱
先考虑暴力dp
1):dp[i][j]由dp[i-1][j]直接转移过来,dp[i][j]=max(dp[i][j],dp[i-1][j])
2):直接从0开始买股票 dp[i][j]=max(dp[i][j],j*AP) (0<j≤MaxP)
3):买股票,股票从 k 张变为 j 张,dp[i][j]=max(dp[i][j],dp[i-W-1][k]-(j-k)*AP)
4):卖股票,股票从 k 张变成 j 张,dp[i][j]=max(dp[i][j],dp[i-W-1][k]+(k-j)*BP)
然后因为这是暴力dp转移,复杂度是T*MaxP*MaxP,可以得到70pts的好成绩
单调队列优化
把式子拆开可得如下(暴力代码注释)
dp[i][j]=max(dp[i][j],dp[i-W-1][k]-AP*j+AP*k);
dp[i][j]=max(dp[i][j],(dp[i-W-1][k]+AP*k)-AP*j)
所以可以维护一个单调队列,(dp[i-W-1][k]+AP*k)最大的单调队列队首
另一个同理
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
using namespace std;
typedef long long LL;
const int maxn=2000+10;
const int INF=0x3f3f3f3f;
/*
这道题的状态转移有额外添加一个转移状态k 前面有道题也是这样
数据范围与提示:
对于 30% 的数据,0≤W<T≤50,1≤MaxP≤50;
对于 50% 的数据,0≤W<T≤2000,1≤MaxP≤50;
对于 100% 的数据,0≤W<T≤2000,1≤MaxP≤2000,1≤BPi?≤APi?≤1000,1≤ASi?,BSi?≤MaxP。
sol:一本通居然没有数据范围太优秀了
很容易发现可以dp,dp[i][j]表示到第i个位置,有j张股票最多赚多少钱
先考虑暴力dp
1):dp[i][j]由dp[i-1][j]直接转移过来,dp[i][j]=max(dp[i][j],dp[i-1][j])
2):直接从0开始买股票 dp[i][j]=max(dp[i][j],j*AP) (0<j≤MaxP)
3):买股票,股票从 k 张变为 j 张,dp[i][j]=max(dp[i][j],dp[i-W-1][k]-(j-k)*AP)
4):卖股票,股票从 k 张变成 j 张,dp[i][j]=max(dp[i][j],dp[i-W-1][k]+(k-j)*BP)
然后因为这是暴力dp转移,复杂度是T*MaxP*MaxP,可以得到70pts的好成绩
单调队列优化
把式子拆开可得如下(暴力代码注释)
dp[i][j]=max(dp[i][j],dp[i-W-1][k]-AP*j+AP*k);
dp[i][j]=max(dp[i][j],(dp[i-W-1][k]+AP*k)-AP*j)
所以可以维护一个单调队列,(dp[i-W-1][k]+AP*k)最大的单调队列队首
另一个同理
*/
int t,w,maxp;
int ap,bp,as,bs;
int dp[maxn][maxn];
struct node{
int pos,zhi;
}q[maxn];
int main(){
scanf("%d %d %d",&t,&maxp,&w);
memset(dp,-63,sizeof(dp));//极小值
for(int i=1;i<=t;i++){
scanf("%d %d %d %d",&ap,&bp,&as,&bs);
//预处理
for(int j=1;j<=min(as,maxp);j++) dp[i][j]=-j*ap; //买入的花费
for(int j=0;j<=maxp;j++) dp[i][j]=max(dp[i][j],dp[i-1][j]); //这里的最大值就不用考虑as了 因为是从上一个状态转移过来的
if(i<=w+1) continue;
int head=1,tail=0;
for(int j=0;j<=maxp;j++){
while(head<tail&&q[head].pos<j-as) head++; //不满足这么多个
while(head<=tail&&dp[i-w-1][j]+ap*j>q[tail].zhi) tail--;
q[++tail].pos=j;q[tail].zhi=dp[i-w-1][j]+ap*j;
dp[i][j]=max(dp[i][j],q[head].zhi-ap*j);
}
head=1;tail=0;
for(int j=maxp;j>=0;j--){
while(head<tail&&q[head].pos>j+bs) head++;
while(head<=tail&&dp[i-w-1][j]+bp*j>q[tail].zhi) tail--;
q[++tail].pos=j;q[tail].zhi=dp[i-w-1][j]+bp*j;
dp[i][j]=max(dp[i][j],q[head].zhi-bp*j);
}
}
int ans=0;
for(int i=0;i<maxp;i++) ans=max(ans,dp[t][i]);
printf("%d\n",ans);
return 0;
}
/*
如果是直接dp不优化的话:
for(j=1;j<=MaxP;j++)
{
for(k=max(j-AS,0);k<j;k++)
{
dp[i][j]=max(dp[i][j],dp[i-W-1][k]-AP*(j-k));
//
// dp[i][j]=max(dp[i][j],dp[i-W-1][k]-AP*j+AP*k);
// dp[i][j]=max(dp[i][j],(dp[i-W-1][k]+AP*k)-AP*j)
// (dp[i-W-1][k]+AP*k)最大的单调队列队首
//
}
}
for(j=0;j<MaxP;j++)
{
for(k=j+1;k<=min(MaxP,j+BS);k++)
{
dp[i][j]=max(dp[i][j],dp[i-W-1][k]+(BP*(k-j)));
//dp[i][j]=max(dp[i][j],dp[i-W-1][k]+BP*k-BP*j);
//dp[i][j]=max(dp[i][j],(dp[i-W-1][k]+BP*k)-BP*j);
// (dp[i-W-1][k]+BP*k)最大的单调队列队首
}
}
}
*/
董老师的例题:
P1725 琪露诺
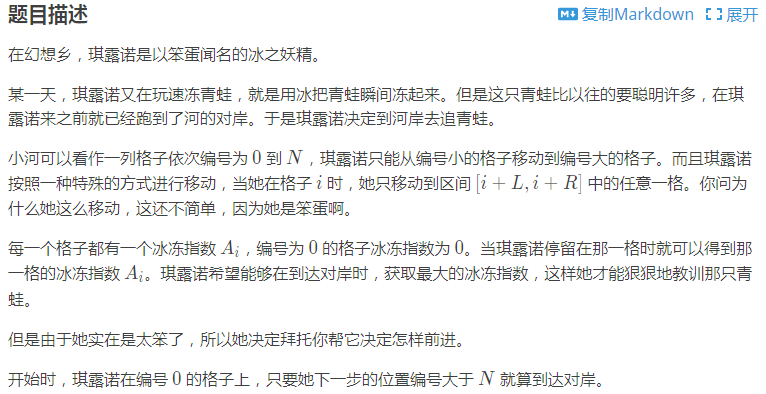
可以倒着想,如果现在在i,那么可以从哪里跳过来

#include<queue>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
const int maxn=2e5+10;
typedef long long LL;
using namespace std;
int n,l,r;
int a[maxn],q[maxn],f[maxn];
int main(){
scanf("%d %d %d",&n,&l,&r);
for(int i=0;i<=n;i++){
scanf("%d",&a[i]);
}
int head=0,tail=0;
memset(f,-0x3f,sizeof(f));
f[0]=0;
int ans=-7e9;
for(int i=l;i<=n;i++){
while(head<=tail&&f[q[tail]]<=f[i-l]) tail--;
q[++tail]=i-l;
while(q[head]<i-r) head++;
f[i]=f[q[head]]+a[i];
if(i>n-r) ans=max(ans,f[i]);
}
printf("%d\n",ans);
return 0;
}
CF372C Watching Fireworks is Fun


注意要从两个方向枚举
(这两道题我都有点不太确定怎么弄状态,但是其实很明显hh)需要枚举的
#include<queue>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
//其实这个状态不是不好想,因为其实就两个明显的,位置和烟火数
//f[i][j]表示放第i个烟火时,在j这个位置所能获得的最大快乐值
const int maxn=150010,maxm=310;
typedef long long LL;
using namespace std;
LL n,m,d,a[maxm],b[maxm],ti[maxm];
LL f[2][maxn],q[maxn];
//用了滚动数组,不然要爆空间
int main(){
cin>>n>>m>>d;
for(int i=1;i<=m;i++){
cin>>a[i]>>b[i]>>ti[i];
}
memset(f,-0x3f,sizeof(f)); //赋值为极小值
for(int i=1;i<=n;i++) f[0][i]=0; //在第0个烟火时。都是为0
for(int i=1;i<=m;i++){
int now=i&1;
int last=(i-1)&1;
int head=1,tail=0;
for(int j=1;j<=n;j++){ //第j位置 窗口右滑
while(head<=tail&&f[last][q[tail]]<=f[last][j]) tail--;
q[++tail]=j;
while(q[head]<j-(ti[i]-ti[i-1])*d) ++head;
f[now][j]=f[last][q[head]]+b[i]-abs(a[i]-j);
}
head=1,tail=0;
for(int j=n;j>=1;j--){
while(head<=tail&&f[last][q[tail]]<=f[last][j]) tail--;
q[++tail]=j;
while(q[head]>j+(ti[i]-ti[i-1])*d) ++head;
f[now][j]=max(f[now][j],f[last][q[head]]+b[i]-abs(a[i]-j));
}
}
LL ans=-1e18;
for(int i=1;i<=n;i++) ans=max(ans,f[m&1][i]);
cout<<ans;
return 0;
}
P2254 [NOI2005] 瑰丽华尔兹

董老师讲得很好,有大致的运行过程

#include<queue>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
typedef long long LL;
const int maxn=205;
using namespace std;
int dx[5]={0,-1,1,0,0},dy[5]={0,0,0,-1,1};
int n,m,sx,sy,k,ans,f[maxn][maxn];
struct node{
int f,pos;
}q[maxn];
char mp[maxn][maxn];
void dp(int x,int y,int l,int tim,int d){
int head=1,tail=0;
for(int i=1;i<=l;i++,x+=dx[d],y+=dy[d]){
if(mp[x][y]=='x'){
head=1;tail=0; //遇到障碍,清空队列
}
else{
while(head<=tail&&q[tail].f+i-q[tail].pos<=f[x][y]) tail--;
q[++tail]=node{f[x][y],i};
while(q[head].pos<i-tim) head++;
f[x][y]=q[head].f+i-q[head].pos;
ans=max(ans,f[x][y]);
}
}
}
int main(){
scanf("%d %d %d %d %d",&n,&m,&sx,&sy,&k);
for(int i=1;i<=n;i++) scanf("%s",mp[i]+1);
memset(f,-0x3f,sizeof(f)); //赋一个最小值,因为求最大
f[sx][sy]=0; //只有起点不一样
for(int K=1,s,t,d,tim;K<=k;K++){
scanf("%d %d %d",&s,&t,&d);
tim=t-s+1;
if(d==1) for(int i=1;i<=m;i++) dp(n,i,n,tim,d); //上
if(d==2) for(int i=1;i<=m;i++) dp(1,i,n,tim,d); //下
if(d==3) for(int i=1;i<=n;i++) dp(i,m,m,tim,d); //左
if(d==4) for(int i=1;i<=n;i++) dp(i,1,m,tim,d); //右
}
printf("%d",ans);
return 0;
}


 posted on
posted on

 浙公网安备 33010602011771号
浙公网安备 33010602011771号