原文链接:https://blog.csdn.net/qq_41730082/article/details/86305056
例题:https://blog.csdn.net/qq_36038511/article/details/82906874

董老师依旧yyds 听得透透的! 这题是打印文章
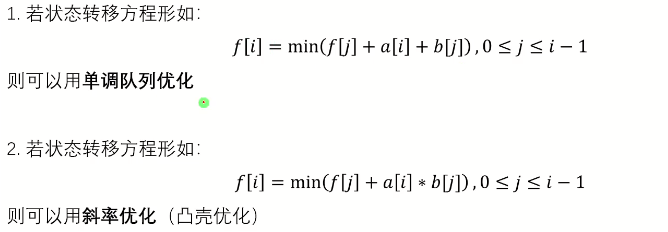

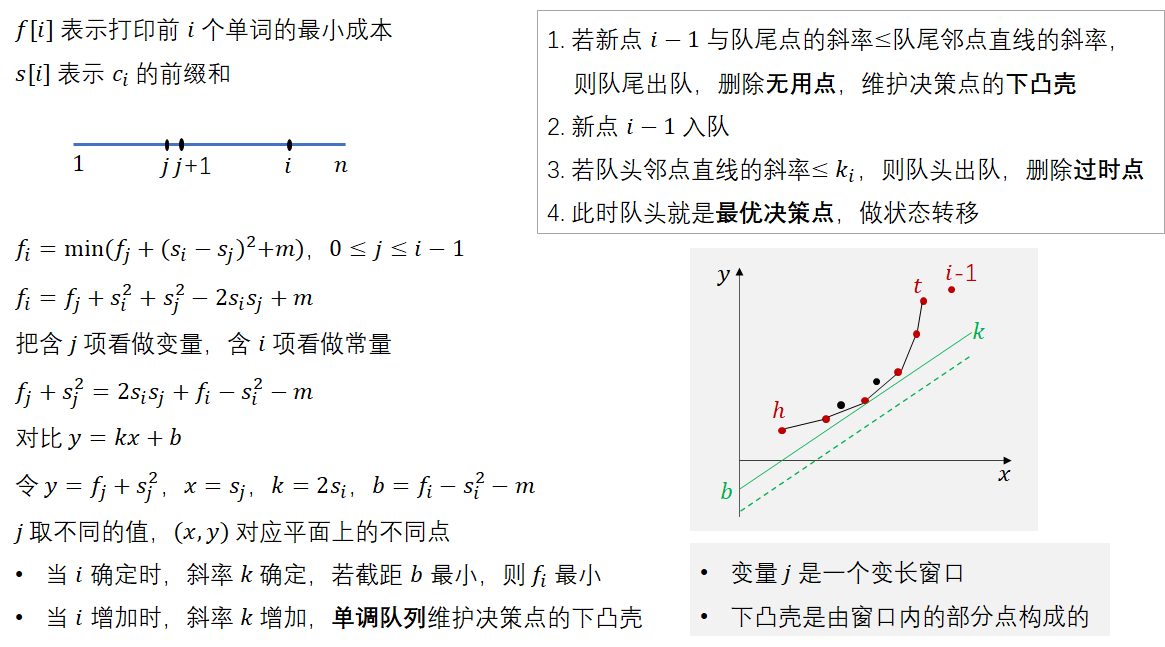
可以直接算斜率,也可以用下面的方式,乘起来,就不用double了
// Luogu P5905 【模板】Johnson 全源最短路
#include<algorithm>
#include<cstring>
#include<iostream>
#include<queue>
#define N 500010
#define INF 1000000000
typedef long long LL;
using namespace std;
int n,m,q[N];
LL s[N],f[N];
double slope(int i,int j){
return (double)(f[i]+s[i]*s[i]-f[j]-s[j]*s[j])/(s[i]==s[j]?1e-9:s[i]-s[j]); //要特判,斜率为无穷大的情况
}
int main(){
while(~scanf("%d %d",&n,&m)){
for(int i=1;i<=n;i++) {
scanf("%d",&s[i]);
s[i]+=s[i-1];
}
int head=1,tail=0;
for(int i=1;i<=n;i++){
while(head<tail&&slope(i-1,q[tail])<=slope(q[tail],q[tail-1])) tail--;
//head<tail 保证队列里面有两个,才可以求出斜率
q[++tail]=i-1;
while(head<tail&&slope(q[head+1],q[head])<=2*s[i]) head++;
int j=q[head];
f[i]=f[j]+(s[i]-s[j])*(s[i]-s[j])+m;
}
printf("%lld\n",f[n]);
}
return 0;
}
1606:【 例 1】任务安排 1
道题如果是用普通的dp你会不会做呢?
普通的dp的话复杂度是O(N^3)的,用dp[i][j]表示前i个任务划分了j段
那么普通的转移表达式就是:dp[i][j]=min(dp[i][j],dp[k][j-1]+(time_sum[i]+s*j)*(cost_sum[i]-cost_sum[k])) j-1<=k<=i-1
其实在后面不知道怎么推的时候,也可以先暴力写出表达式,找找思路
一看就是个 dp了,设 f[i]为前i个任务的最小花费。
发现题目中的 s不好处理,这里用到一个很优秀的技巧——费用提前。
具体是这样的:因为我们不知道之前用了多少个s,所以这里难以计算费用,换句话说,我们不知道之前对现在的贡献,但是,我们知道现在对未来的贡献!
假如当前把 x~y 这一段任务一起完成,那么事实上,我们将x~n 这一段任务的完成时间都延后了s,那么直接加上 (c[n]-c[x-1])×s ,c是任务费用系数的前缀和)即可。
那么得出方程:f[i]=mini({f[j]+(s[i]+s)×(c[i]-c[j])+s×(c[n]-c[j])} t 是任务的时间花费的前缀和
//这道题如果是用普通的dp你会不会做呢?
//普通的dp的话复杂度是O(N^3)的,用dp[i][j]表示前i个任务划分了j段
//那么普通的转移表达式就是:
//dp[i][j]=min(dp[i][j],dp[k][j-1]+(time_sum[i]+s*j)*(cost_sum[i]-cost_sum[k])) j-1<=k<=i-1
/*
一看就是个 dp了,设 f[i]为前i个任务的最小花费。
发现题目中的 s不好处理,这里用到一个很优秀的技巧——费用提前。
具体是这样的:因为我们不知道之前用了多少个s,所以这里难以计算费用,换句话说,我们不知道之前对现在的贡献,但是,我们知道现在对未来的贡献!
假如当前把 x~y 这一段任务一起完成,那么事实上,我们将x~n 这一段任务的完成时间都延后了s,那么直接加上 (c[n]-c[x-1])×s,c是任务费用系数的前缀和)即可。
那么得出方程:f[i]=mini({f[j]+(s[i]+s)×(c[i]-c[j])+s×(c[n]-c[j])} t 是任务的时间花费的前缀和
*/
//求出T和F的前缀和st和sf,设f[i]表示完成前i个任务的最小费用,f[i]=min(f[i],f[j]+st[i](sf[i]-sf[j])+s (st[n]-st[j])),因为s的会对后j+1~n个任务产生影响所以提前累加。
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
int list[5100];
long long f[5100],t[5100],c[5100];
int main()
{
int n,S;
scanf("%d%d",&n,&S);
for (int i=1;i<=n;i++)
{
long long tt,cc;
scanf("%lld%lld",&tt,&cc);
t[i]=t[i-1]+tt;
c[i]=c[i-1]+cc;
}
memset(f,63,sizeof(f));
f[0]=0;
for (int i=1;i<=n;i++)
{
for (int j=0;j<i;j++)
{
f[i]=min(f[j]+(t[i]+S)*(c[i]-c[j])+(c[n]-c[i])*S,f[i]);
}
}
printf("%lld\n",f[n]);
return 0;
}
1607:【 例 2】任务安排 2
进阶的做法
//虽然这个上一道题的做法也就是(N^2)也能过
j<k<i,若k比j优 (Ps:为了方便C表示Cost,T表示Time)则dp[k]+S*(C[n]-C[k])+T[i]*(C[i]-C[k])<=dp[j]+S*(C[n]-C[j])+T[i]*(C[i]-C[j])
把括号拆掉 dp[k]+S*C[n]-S*C[k]+T[i]*C[i]-T[i]*C[k]<=dp[j]+S*C[n]-S*C[j]+T[i]*C[i]-T[i]*C[j]
消去同类 dp[k]-S*C[k]-T[i]*C[k]<=dp[j]-S*C[j]-T[i]*C[j]
移项得 dp[k]-dp[j]<=(S+T[i])*(C[k]-C[j]) 条件1
则(条件1)成立时 k 比 j 优 ,否则 j 比 k 优
(dp[k]-dp[j]) / (C[k]-C[j]) 是斜率
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=10010;
const int INF=0x3fffffff;
typedef long long LL;
int n,s;
LL tt[maxn],cost[maxn];
LL dp[maxn];
int que[maxn];
/*
设j<k<i,若k比j优 (Ps:为了方便C表示Cost,T表示Time)
则dp[k]+S*(C[n]-C[k])+T[i]*(C[i]-C[k])<=dp[j]+S*(C[n]-C[j])+T[i]*(C[i]-C[j])
把括号拆掉 dp[k]+S*C[n]-S*C[k]+T[i]*C[i]-T[i]*C[k]<=dp[j]+S*C[n]-S*C[j]+T[i]*C[i]-T[i]*C[j]
消去同类 dp[k]-S*C[k]-T[i]*C[k]<=dp[j]-S*C[j]-T[i]*C[j]
移项得 dp[k]-dp[j]<=(S+T[i])*(C[k]-C[j]) 条件1
则(条件1)成立时 k 比 j 优 ,否则 j 比 k 优
(dp[k]-dp[j]) / (C[k]-C[j]) 是斜率
*/
bool judge(int j,int k,int i){ //j<k<i,判断k是不是更优 (dp[k]-dp[j]) / (C[k]-C[j]) 是斜率
int s1=dp[k]-dp[j];
int s2=(s+tt[i])*(cost[k]-cost[j]);
return s1<=s2 ? 1:0;
}
bool judge1(int j,int k,int i){ //j<k<i,
int s1=(dp[k]-dp[j])*(cost[i]-cost[k]);
int s2=(dp[i]-dp[k])*(cost[k]-cost[j]);//交换看看,其实是除法
return s1>=s2 ? 1:0;
}
int main(){
scanf("%d %d",&n,&s);
for(int i=1;i<=n;i++){
int t,cc;
scanf("%d %d",&t,&cc);
tt[i]=tt[i-1]+t;
cost[i]=cost[i-1]+cc;
}
dp[0]=0;
que[1]=0;
int head=1,tail=1;
for(int i=1;i<=n;i++){
while(head<tail&&judge(que[head],que[head+1],i)) head++;
int j=que[head];
dp[i]=dp[j]+s*(cost[n]-cost[j])+tt[i]*(cost[i]-cost[j]);
while(head<tail&&judge1(que[tail-1],que[tail],i)) tail--;
que[++tail]=i;
}
printf("%lld\n",dp[n]);
return 0;
}
1608:【 例 3】任务安排 3
t数组不再具有单调性,所以需要二分。而我们要维护斜率还是具有单调性的!!结束删队头的操作,最后出来的list[head]左边的斜率小于t[i],右边的斜率大于t[i]
所以通过 二分查找到 左边的斜率小于t[i],右边的斜率大于t[i]的点
这次的Ti可以是负的,所以就没有单调性了,但是凸包还是有单调性的,所有二分当前直线与凸包的切点就可以了(题解原话)
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=310000;
const int INF=0x3fffffff;
typedef long long LL;
//时间可能为负数,因此时间的前缀和t[i]也不具有单调性
//而我们要维护斜率还是具有单调性的!!
//结束删队头的操作,最后出来的list[head]左边的斜率小于t[i],右边的斜率大于t[i]
//所以通过 二分查找到 左边的斜率小于t[i],右边的斜率大于t[i]的点
//这次的Ti可以是负的,所以就没有单调性了,但是凸包还是有单调性的,所有二分当前直线与凸包的切点就可以了(题解原话)
//为什么是二分,没想明白
int n,s;
LL dp[maxn],t[maxn],c[maxn],list[maxn];
LL X(int i){
return c[i];
}
LL Y(int i){
return dp[i]-s*c[i];
}
double slop(int j1,int j2){
return double(Y(j2)-Y(j1))/double(X(j2)-X(j1));
}
int main(){
scanf("%d %d",&n,&s);
for(int i=1;i<=n;i++){
int tt,cc;
scanf("%d %d",&tt,&cc);
t[i]=t[i-1]+tt;
c[i]=c[i-1]+cc;
}
int head=1,tail=1;
list[1]=0;
for(int i=1;i<=n;i++){
//这里不再弹队头,因为t不具有单调性了
int l=head,r=tail; //二分找
while(l<r){
int mid=(l+r)/2;
if(dp[list[mid]]-dp[list[mid+1]]>=(s+t[i])*(c[list[mid]]-c[list[mid+1]])) l=mid+1;
else r=mid;
}
dp[i]=dp[list[l]]-(s+t[i])*c[list[l]]+t[i]*c[i]+s*c[n]; //你仔细看,是另一种计算方法
while (head<=tail-1&&(dp[list[tail]]-dp[list[tail-1]])*(c[i]-c[list[tail]])>=(dp[i]-dp[list[tail]])*(c[list[tail]]-c[list[tail-1]])) tail--;
list[++tail]=i;
}
printf("%lld\n",dp[n]);
return 0;
}
1609:【例 4】Cats Transport
这次的dp数组变为二维了,我觉得最重要的是要想到对数组a[]进行排序,然后就转化为每个人取连续的一段。
这个思路是我欠缺的,因为人数增多了,最后返回的答案也是dp[p][m]
ps.下面写错了,Y()应该是相加

#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=1e5+10;
const int INF=0x3fffffff;
typedef long long LL;
LL d[maxn],a[maxn],s[maxn],list[maxn];
LL dp[110][maxn]; //dp[饲养员i][收回前j只猫]
LL X(int i){
return i;
}
LL Y(int i,int k){
return dp[i][k]+s[k];
}
bool cmp(LL x,LL y){
return x<y;
}
int main(){
int n,m,p;
scanf("%d %d %d",&n,&m,&p);
for(int i=2;i<=n;i++) {
scanf("%d",&d[i]);
d[i]+=d[i-1];
}
int h,t;
for(int i=1;i<=m;i++){
scanf("%d %d",&h,&t);
a[i]=t-d[h];
}
sort(a+1,a+1+m,cmp) ; //对a进行排序 对a排序,根据贪心策略,一个饲养员接到的猫一定是a[]排序后连续的一段,那么此时问题又回到了任务安排2了
for(int i=1;i<=m;i++){
s[i]=s[i-1]+a[i]; //s是a的前缀和
}
memset(dp,63,sizeof(dp));
for(int i=0;i<=p;i++) dp[i][0]=0; //初始化
for(int i=1;i<=p;i++){ //进行p次 每次都去一段连续的
int head=1,tail=1;
list[1]=0;
for(int j=1;j<=m;j++){
while(head<tail&&(Y(i-1,list[head])-Y(i-1,list[head+1]))>=a[j]*(list[head]-list[head+1])) head++;
dp[i][j]=min(dp[i-1][j],dp[i-1][list[head]]+a[j]*(j-list[head])-(s[j]-s[list[head]]));
if(dp[i-1][j]+s[j]>=455743088879883099) continue;
while(head<tail&&((Y(i-1,list[tail-1])-Y(i-1,list[tail]))*(list[tail]-j)>(Y(i-1,list[tail])-Y(i-1,j))*(list[tail-1]-list[tail]))) tail--;
//逐一比较,直到队列的节点不剩下的时候(其实那会应该剩下一个我们最初放入的0号节点,保证了可能是从第一位开始向后加的情况的元素),
//或者是K1>K2的时候,我们结束循环,并且继续下一个元素。
list[++tail]=j;
}
}
printf("%lld\n",dp[p][m]);
return 0;
}
1610:玩具装箱
https://www.cnblogs.com/gaojunonly1/p/10409738.html

#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=5e4+10;
const int INF=0x3fffffff;
typedef long long LL;
//典型题
int n,l;
LL c[maxn],dp[maxn],list[maxn];
LL sqr(LL x) {
return x*x;
}
LL X(int i){
return c[i];
}
LL Y(int i){
return dp[i]+sqr(c[i]);
}
int main(){
scanf("%d %d",&n,&l);
for(int i=1;i<=n;i++){
int cc;
scanf("%d",&cc);
c[i]=c[i-1]+cc+1; //因为要每个玩具之间有点间距,所以要加1
}
int head=1,tail=1;
list[0]=0;
l++;
for(int i=1;i<=n;i++){
//这里就相当于k1--head k2--head+1(k1<k2)
while(head<tail&&((Y(list[head])-Y(list[head+1]))>=2*(c[i]-l)*(X(list[head])-X(list[head+1])))) head++;
dp[i]=dp[list[head]]+sqr(c[i]-c[list[head]]-l);
//这里需要满足斜率递增的条件,不然取不到最优
//相当于 tail-1到tail的斜率如果大于了 i到tail的斜率 那么就需要去除掉最后的tail
while(head<tail&&(( Y(list[tail-1]) - Y(list[tail])) * (X(list[tail])-X(i)) >= ( Y(list[tail]) - Y(i)) * (X(list[tail-1]) - X(list[tail]))))tail--;
//(head<=tail-1 && ( Y(list[tail-1]) - Y(list[tail])) * (X(list[tail])-X(i)) >= ( Y(list[tail]) - Y(i)) * (X(list[tail-1]) - X(list[tail]))) tail--;
list[++tail]=i;
}
printf("%lld",dp[n]);
return 0;
}
1611:仓库建设
一样的,可以先写暴力的式子,然后一步一步推出
另 f[i]=f[j]+Calc(j+1,i),Calc(j+1,i)表示 j+1 到 i 的货物全部运到 i 的花费 这里的重点就是计算calc(j,i)是O(1)的
对于这个暴力统计是这样的:
for(k=j+1;k<=i;k++)
{
int SS=0;
SS+=(Dis[i]-Dis[j])*P[j];
}
设一个 Val[i]=Val[i-1]+P[i]*Dis[i]; 和一个P_Qzh[i]=P_Qzh[i-1]+P[i];
SS就是Calc(j+1,i),容易发现SS=Dis[i]*(P_Qzh[i]-P_Qzh[j])-(Val[i]-Val[j]);
然后就有了n2的暴力
然后套路的用斜率优化,过程如下
j<k<i (若k比j优)
dp[j]+Cost[i]+Dis[i]*(P_Qzh[i]-P_Qzh[j])-(Val[i]-Val[j]) (1)
--->dp[j]+Cost[i]+Dis[i]*P_Qzh[i]-Dis[i]*P_Qzh[j]-Val[i]+Val[j]
dp[k]+Cost[i]+Dis[i]*(P_Qzh[i]-P_Qzh[k])-(Val[i]-Val[k]) (2)
--->dp[k]+Cost[i]+Dis[i]*P_Qzh[i]-Dis[i]*P_Qzh[k]-val[i]+Val[k]
若(1)>=(2)
---> dp[k]-Dis[i]*P_Qzh[k]+Val[k] <= dp[j]-Dis[i]*P_Qzh[j]+Val[j]
---> (dp[k]+Val[k])-(dp[j]+Val[j]) <= Dis[i]*(P_Qzh[k]-P_Qzh[j])
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=1e6+10;
const int INF=0x3fffffff;
typedef long long LL;
//当一下子写不出来状态表达式时
//可以先试试用暴力思考,然后一步步分解这个表达式
int n;
LL dis[maxn],pp[maxn],a[maxn],dp[maxn];
//pp是p(货物个数)的前缀和,a是p[i]*dis[i]的前缀和
int list[maxn],c[maxn],p[maxn];
//p是个数、c是建造的金额
LL X(int i){
return pp[i];
}
LL Y(int i){
return dp[i]+a[i];
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d %d %d",&dis[i],&p[i],&c[i]);
pp[i]=pp[i-1]+p[i];
a[i]=a[i-1]+dis[i]*p[i];
}
int head=1,tail=1;
list[0]=0;
for(int i=1;i<=n;i++){
while(head<tail&&(Y(list[head])-Y(list[head+1]))>=dis[i]*(X(list[head])-X(list[head+1]))) head++;
dp[i]=dp[list[head]]+(pp[i]-pp[list[head]])*dis[i]-(a[i]-a[list[head]])+c[i];
while(head<tail&&(Y(list[tail-1])-Y(list[tail]))*(X(list[tail])-X(i))>=(Y(list[tail])-Y(i))*(X(list[tail-1])-X(list[tail]))) tail--;
list[++tail]=i;
}
printf("%lld",dp[n]);
return 0;
}
//有两个点超时了???? 试了试其他代码也是超市
1612:特别行动队
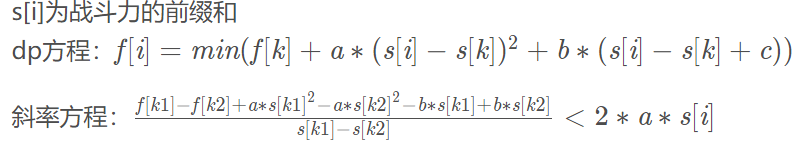
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=1100000;
const int INF=0x3fffffff;
typedef long long LL;
int n,a,b,c;
int list[maxn];
LL dp[maxn],s[maxn];
LL sqr(LL x){
return x*x;
}
LL X(int i){
return s[i];
}
LL Y(int i){
return dp[i]+a*sqr(s[i])-b*s[i];
}
int main(){
scanf("%d %d %d %d",&n,&a,&b,&c);
for(int i=1;i<=n;i++){
scanf("%d",&s[i]);
s[i]+=s[i-1];
}
int head=1,tail=1;
list[0]=0;
for(int i=1;i<=n;i++){
while(head<tail&&(Y(list[head])-Y(list[head+1]))<(2*a*s[i])*(X(list[head])-X(list[head+1]))) head++;
dp[i]=dp[list[head]]+a*sqr(s[i]-s[list[head]])+b*(s[i]-s[list[head]])+c;
while(head<tail&&(Y(list[tail-1])-Y(list[tail]))*(X(list[tail])-X(i))<(Y(list[tail])-Y(i))*(X(list[tail-1])-X(list[tail]))) tail--;
list[++tail]=i;
}
printf("%lld",dp[n]);
return 0;
}
1613:打印文章
这个也是例题了
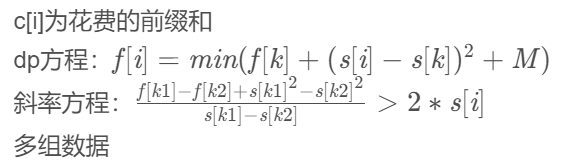
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define LL long long
const int maxn=5e5+100;
//这道题最重要的是怎么推出两个工厂之间的花费公式
LL s[maxn],f[maxn],list[maxn];
int n,m;
LL X(int i){
return s[i];
}
LL Y(int i){
return f[i]+s[i]*s[i];
}
int main(){
while(scanf("%d %d",&n,&m)!=EOF){
s[0]=0;
int x;
for(int i=1;i<=n;i++){
scanf("%d",&x);
s[i]=s[i-1]+x;
}
int head=1,tail=1;
list[1]=0;
f[0]=0;
for(int i=1;i<=n;i++){
while(head<tail&&(Y(list[head])-Y(list[head+1]))>=2*s[i]*(X(list[head])-X(list[head+1]))) head++;
f[i]=f[list[head]]+(s[i]-s[list[head]])*(s[i]-s[list[head]])+m;
while(head<tail&&(Y(list[tail-1])-Y(list[tail]))*(X(list[tail])-X(i))>=(Y(list[tail])-Y(i))*((X(list[tail-1]))-X(list[tail]))) tail--;
list[++tail]=i;
}
printf("%lld\n",f[n]);
}
return 0;
}
1614:锯木厂选址
这道题的代价计算公式和前面的仓库建设一样,主要是怎么推的

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define LL long long
LL f[210000],w[210000],d[210000],a[210000];
int list[210000];
LL Y(LL i) {return w[i]*d[i];}
LL X(LL i) {return w[i];}
int main()
{
int n;
scanf("%d",&n);
for (int i=1;i<=n;i++)
{
int x,y;
scanf("%d%d",&x,&y);
d[i+1]=d[i]+y;
a[i+1]=a[i]+x*d[i];
w[i]=w[i-1]+x;
}
int head=1,tail=1; //list[1]=1; f[1]=a[n]-a[1];
LL ans=9223372036854775807;
for (int i=1;i<=n;i++)
{
while (head+1<=tail&& (Y(list[head]) - Y(list[head+1])) >= d[i] * (X(list[head]) - X(list[head+1]))) head++;
f[i]=w[list[head]]*d[list[head]]-a[list[head]]+(w[i]-w[list[head]])*d[i]-(a[i]-a[list[head]])+(w[n]-w[i])*d[n+1]-(a[n+1]-a[i]);
while (head<=tail-1&& (Y(list[tail-1]) - Y(list[tail])) * (X(list[tail]) - X(i)) >= (Y(list[tail]) - Y(i)) * (X(list[tail-1]) - X(list[tail]))) tail--;
list[++tail]=i;
ans=min(ans,f[i]);
}
printf("%lld\n",ans);
return 0;
}


 posted on
posted on

 浙公网安备 33010602011771号
浙公网安备 33010602011771号