3、数论
3.1 最小公倍数 GCD
int gcd(int a,int b){
//辗转相除
if(b==0) return a;
else return gcd(b,a%b);
}
int gcd(int a,int b){
return !b ? a:gcd(b,a%b);
}
最大公约数 LCM
lcm(a,b)=a*b/gcd(a,b)
3.2 快速幂
快速幂及扩展的矩阵快速幂,快速计算a^n的值
两种方法
//分治
int fastpow(int a,int n){
if(n==1) return a;
int temp=fastpow(a,n/2);
if(n%2==1) return temp*temp*a;
else return temp*temp;
}
//位运算,加上取模
int fastpow(int a,int n,int mod){
int base=a;
int res=1;
while(n){
if(n&1) res=res*base%mod;
base=base*base%mod;
n>>=1;
}
return res;
}
矩阵快速幂,但是难点是把递推关系转化为矩阵的关系,例如:斐波那契数列
struct matrix{
int m[maxn][maxn];
matrix(){
memset(m,0,sizeof(m));
}
};
matrix multi(matrix a,matrix b){
matrix res;
for(int i=0;i<maxn;i++){
for(int j=0;j<maxn;j++){
for(int k=0;k<maxn;k++){
res.m[i][j]=(res.m[i][j]+a.m[i][k]*b.m[k][j])%mod;
}
}
}
return res;
}
matrix fastm(martix a,int n){
matrix res;
for(int i=0;i<maxn;i++)
res.m[i][i]=1; //初始化为单位矩阵 就像res=1
while(n){
if(n&1) res=multi(res,a);
a=multi(a,a);
n>>=1;
}
return res;
}
3.3 求素数
普通的做法(试除法),即从2~sqrt(n)之内判断的----n<=10^12 以内可以接受 O(√N)
判断:[2,sqrt(n)]内的所有数-----[2,sqrt(n)]内的所有素数
bool is_prime(int n){
if(n==1) return false;
for(int i=2;i*i<=n;i++){
if(n%i==0) return false;
}
return true;
}
1、埃氏筛法:O(NlongNlongN)
因为空间用到了is[maxn],所以当maxn=1e7时是可以接受的,不然空间就太大了
优化(1)用来做筛的数到sqrt(n)就可以了(2)for(int j=i+i 可以改为j=i*i,因为前面已经筛过了
int prime[maxn];
bool is[maxn];
int ans=0;
void findd(){
for(int i=2;i*i<=maxn;i++){ //是<
if(is[i]==0){
prime[ans++]=i;
for(int j=i*i;j<maxn;j+=i){
p[j]=1;
}
}
}
}
2、线性筛模板 O(N) 让每个数只被自己的最小质因数筛一次
void prim(){
for(int i=2;i<=n;i++){
if(!vis[i]){
prime[++ans]=i;
}
for(int j=1;j<=ans&&prime[j]*i<=n;j++){
vis[prime[j]*i]=1;
if(i%prime[j]==0) break;
}
}
}
- 大区间素数
埃氏筛法能解决n<=1e7的问题,但是如果n更大,那么就可以扩展位大区间素数,例如求区间[a,b]内的素数,a<b<=1e12, b-a<=1e6
先用埃氏筛法求出[2,sqrt(b)]范围内的素数,再用这些素数去筛空间[a,b]内的素数
题目:1619: 【例 1】Prime Distance
【以下代码都是来自董老师yyds】
- 筛法求欧拉函数


#include<iostream>
using namespace std;
const int maxn=1e9;
int phi(int n){
int res=n;
for(int i=2;i*i<=n;i++){ //试除法求欧拉函数
if(n%i==0){
res=res/i*(i-1);
while(n%i==0) n/=i;
}
}
if(n>1) res=res*n/(n-1);
return res;
}
int main(){
int n;
cin>>n;
cout<<phi(n)<<endl;
return 0;
}
#include <iostream>
using namespace std;
const int N = 1000010;
int p[N], vis[N], cnt;
int phi[N];
void get_phi(int n){//筛法求欧拉函数
phi[1] = 1;
for(int i=2; i<=n; i++){
if(!vis[i]){
p[cnt++] = i;
phi[i] = i-1;
}
for(int j=0; i*p[j]<=n; j++){
int m = i*p[j];
vis[m] = 1;
if(i%p[j] == 0){
phi[m] = p[j]*phi[i];
break;
}
else
phi[m]=(p[j]-1)*phi[i];
}
}
}
int main(){
int n;
cin >> n;
get_phi(n);
for(int i=1; i<=n; i++)
printf("%d\n", phi[i]);
return 0;
}
- 筛法求约数个数(1~n)
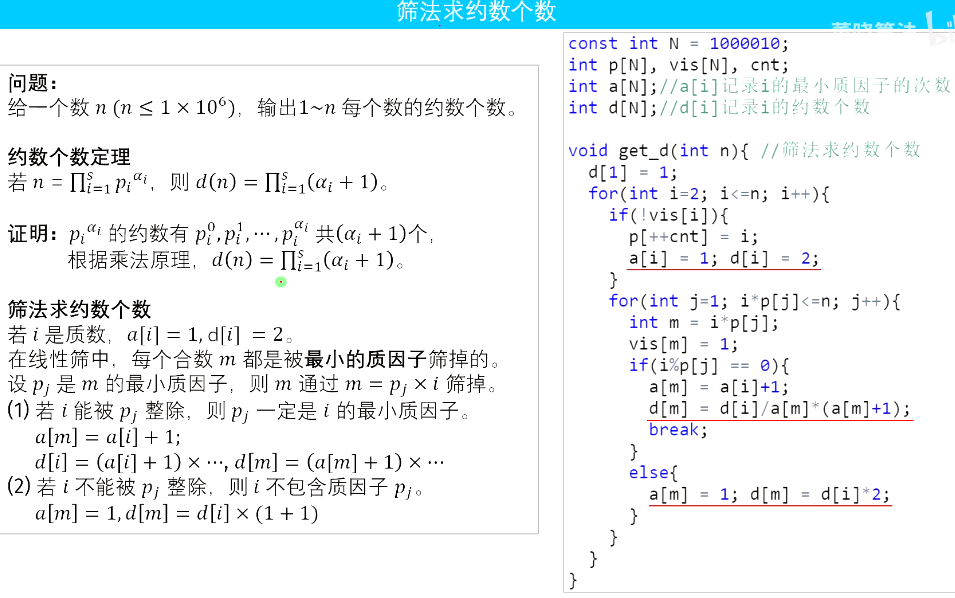
#include<iostream>
using namespace std;
const int maxn= 1000010;
int p[maxn],vis[maxn],cnt;
int a[maxn]; //a[i]记录i的最小质因子的次数
int d[maxn]; //d[i]记录i的约数个数
void get_d(int n){
d[1]=1;
for(int i=2;i<=n;i++){
if(!vis[i]){
p[++cnt]=i;
a[i]=1;d[i]=2;
}
for(int j=1;i*p[j]<=n;j++){
int m=i*p[j];
vis[m]=1;
if(i%p[j]==0){
a[m]=a[i]+1;
d[m]=d[i]/a[m]*(a[m]+1);
break;
}
else{
a[m]=1;
d[m]=d[i]*2;
}
}
}
}
int main(){
int n;
cin>>n;
get_d(n);
for(int i=1;i<=n;i++) cout<<i<<" "<<d[i]<<endl;
}
- 筛法求约数和

#include<iostream>
using namespace std;
const int maxn= 1000010;
int p[maxn],vis[maxn],cnt;
int g[maxn],f[maxn];
////g[i]表示i的最小质因子的1+p^1+...+p^k
//f[i]表示i的约数和
void get_f(int n){
g[1]=f[1]=1;
for(int i=2;i<=n;i++){
if(!vis[i]){
p[++cnt]=i;
g[i]=f[i]=i+1;
}
for(int j=1;i*p[j]<=n;j++){
int m=i*p[j];
vis[m]=1;
if(i%p[j]==0){
g[m]=g[i]*p[j]+1;
f[m]=f[i]/g[i]*g[m];
break;
}
else{
g[m]=p[j]+1;
f[m]=f[i]*g[m];
}
}
}
}
int main(){
int n;
cin>>n;
get_f(n);
for(int i=1;i<=n;i++) cout<<i<<": "<<f[i]<<endl;
}
裴蜀定理----->推出扩展欧几里得


https://www.luogu.com.cn/problem/P4549
#include<iostream>
#include<cstdio>
#include<cmath>
typedef long long LL;
//const int maxn=1000001;
//const int mx=3000008;
using namespace std;
int n,s,a;
int gcd(int a,int b){
if(b==0) return a;
else return gcd(b,a%b);
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a;
s=gcd(s,abs(a));
}
cout<<s;
}
3.4 扩展欧几里得算法与二元一次方程的整数解
给出整数a,b,n,问方程ax+by=n什么时候有整数解
!!!有解的充要条件是gcd(a,b)可以整除n
如果确定有解,那么解题方法是先找到一个可行解(x0,y0),然后用通解公式
x=x0+bt
y=y0-at求解,那么问题就是如何求(x0,y0)
扩展欧几里得方法:当方程符合ax+by=gcd(a,b)时,可以用扩展欧几里得算法求(x0,y0)

void extend_gcd(int a,int b,int &x,int &y){
if(b==0){
x=1;y=0;
return;
}
extend_gcd(b,a%b,x,y);
int temp=x;
x=y;
y=temp-(a/b)*y;
}
求出来的x,y就是所得到x0,y0,那么通解公式就是:
x=x0+b/gcd*t gcd=gcd(a,b)
y=y0-a/gcd *t
x对应的最小非负整数解为(x%(b/gcd))+b/gcd)%(b/gcd)
那么问题ax+by=n的整数解
利用上面的结果,步骤如下:
(1)判断ax+by=n是否有整数解,也就是gcd(a,b)能不能整除n
(2)扩展欧几里得求得x0,y0
(3)在ax0+by0=gcd(a,b)两边同时乘以n/gcd(a,b)
(4)对照ax+by=n,得到解为:
x0'=x0*n/gcd(a,b) y0'=y0*n/gcd(a,b)
那么通解公式为:
x=x0'+b/gcd*k
y=y0'-a/gcd *k
运用场合:(1)求解不定方程(2)求解模的逆元(3)求解同余方程
#include<iostream>
#include<cstdio>
#include<cmath>
typedef long long LL;
int exgcd(int a,int b,int &x1,int &y1){
if(b==0){
x=1;y=0;return a;
}
int x1,y1,d;
d=exgcd(b,a%b,x1,y1);
x=y1;
y=x1-a/b*y1;
return d;
}
int main(){
int a,b,c,x,y;
cin>>a>>b>>c;
int d=exgcd(a,b,x,y);
if(c%d==0){
cout<<c/d*x<<" "<<c/d*y<<endl;
}
else cout<<"none"<<endl;
}
3.5 同余与逆元
a%m=b%m,那么a和b对m同余,m称为同余的模,记为m|(a-b),即a-b是m的整数倍,同余的符号记为a=b(mod m) (等号三横)
逆元:给出a,m,求方程ax=1(mod m),即ax除以m的余数为1
有解的条件是gcd(a,m)=1,即a,m互素,等价于求ax+my=1
方程ax=1(mod m)的一个解x,称x为a模m的逆元。这样的x很多,都称为逆
int mod_inverse(int a,int m){
int x,y;
extend_gcd(a,m,x,y);
return (m+x%m)%m; //可能是负数,所以需要处理
}
逆元的应用:除法的模,求(a/b)mod m,a,b很大,但是求除法之后再取模会损失精度
把除法的模运算转换成了乘法模运算
(a/b)modm=((a/b)modm)((bk)modm)=((a/b)*(bk))modm=akmodm
费马小定理


费马小定理加快速幂求乘法逆元
#include<iostream>
#include<cstdio>
#include<string.h>
typedef long long LL;
using namespace std;
int a,p;
int quickpow(LL a,int b,int p){
int res=1;
while(b){
if(b&1) res=res*a%p;
a=a*a%p;
b>>=1;
}
return res;
}
int main(){
cin>>a>>p;
if(a%p){
cout<<quickpow(a,p-2,p)<<endl;
}
return 0;
}
欧拉函数、欧拉定理 剩余系、完全剩余系、简化剩余系

扩展欧拉定理

https://www.luogu.com.cn/problem/P5091
#include <iostream>
using namespace std;
typedef long long LL;
int a,b,m,phi,flag;
char s[20000005];
int get_phi(int n){//求欧拉函数
int res = n;
for(int i=2; i*i<=n; i++){
if(n%i == 0){
res = res/i*(i-1);
while(n%i == 0) n /= i;
}
}
if(n>1) res = res/n*(n-1);
return res;
}
int depow(int phi){//降幂
int b = 0;
for(int i=0; s[i]; i++){
b = b*10+(s[i]-'0');
if(b>=phi) flag=1, b%=phi;
}
if(flag) b += phi;
return b;
}
int qpow(LL a, int b){//快速幂
int res = 1;
while(b){
if(b&1) res = res*a%m;
a = a*a%m;
b >>= 1;
}
return res;
}
int main(){
scanf("%d%d%s", &a, &m, s);
phi = get_phi(m);
b = depow(phi);
printf("%d", qpow(a,b));
return 0;
}
一元线性同余方程
ax=b(mod m),即ax-b是m的整数倍,得到ax+my=b,当且仅当gcd(a,m)能整除b是有解
当gcd(a,m)=b时,能够运用扩展欧几里得方法直接求解ax+my=b
当gcd(a,m)!=b 时,就需要运用逆元
如果a'是a模m的逆,则a'a=1mod(m),那么在ax=b(mod m)两边同时乘以a',那么就是x=a'b(mod m)
步骤:求解ax+my=b 同余方程为ax=b(mod m)
(1)有解的条件:gcd(a,m)能够整除b
(2)求ax=1(mod m)得逆元a',等价于扩展欧几里得算法求出ax+my=1
(3)一个特解是x=a'b
(4)代入方程ax+my=b,求解y
威尔逊定理


https://acm.hdu.edu.cn/showproblem.php?pid=2973
#include<iostream>
#include<cstdio>
typedef long long LL;
const int maxn=1000001;
const int mx=3000008;
int s[maxn],p[maxn],vis[mx],t,n;
void get_prim(){
for(LL i=2;i<mx;i++){
if(!vis[i]){
if((i-7)%3==0) p[(i-7)/3]=1;
}
for(LL j=i*i;j<mx;j+=i) vis[j]=1;
}
}
int main(){
get_prim();
for(int i=2;i<maxn;i++) s[i]=s[i-1]+p[i];
scanf("%d",&t);
while(t--){
scanf("%d",&n);
printf("%d\n",s[n]);
}
}
中国剩余定理(孙子定理)
https://www.cnblogs.com/wkfvawl/p/9633188.html

但是这样的中国剩余定理有一个要求就是m1,m2,m3...mn是互素的

#include<iostream> #include<cstring> #include<cmath> #include<algorithm> #include<stack> #include<cstdio> #include<queue> #include<map> #include<vector> #include<set> using namespace std; const int maxn=1010; const int INF=0x3fffffff; typedef long long LL; typedef unsigned long long ull; LL n; //中国剩余定理(孙子定理) //https://www.cnblogs.com/wkfvawl/p/9633188.html LL aa[12],bb[12]; void extend_gcd(LL a,LL b,LL &x,LL &y){ if(b==0){ x=1; y=0;return; } extend_gcd(b,a%b,x,y); LL tmp=x; x=y; y=tmp-(a/b)*y; } LL gcd(LL x,LL y){ if(y==0) return x; else return gcd(y,x%y); } int main(){ scanf("%lld",&n); LL mod=1; for(int i=1;i<=n;i++){ scanf("%lld %lld",&aa[i],&bb[i]); mod*=aa[i]; } LL ans=0; LL x,y; for(int i=1;i<=n;i++){ LL p=mod/aa[i]; extend_gcd(p,aa[i],x,y); //cout<<x<<endl; ans=(ans+bb[i]*x*p)%mod; } cout<<(ans+mod)%mod; /* 超时到怀疑人生哈哈哈哈 for(LL i=mm;;i++){ bool flag=0; for(int j=1;j<=n;j++){ if(!judge(i-bb[j],aa[j])) { flag=1;break; } } if(!flag){ cout<<i<<endl;break; } } */ return 0; }
扩展中国剩余定理
扩展中国剩余定理跟中国剩余定理没半毛钱关系,一个是用扩展欧几里得,一个是用构造
https://www.cnblogs.com/zwfymqz/p/8425731.html
判定有无解:(两个一次处理)


#include<iostream> #include<cstring> #include<cmath> #include<algorithm> #include<stack> #include<cstdio> #include<queue> #include<map> #include<vector> #include<set> using namespace std; const int maxn=1e5+10; const int INF=0x3fffffff; typedef long long LL; typedef unsigned long long ull; //变形是需要判断有没有解 //中国剩余定理的要求就是:m1,m2....mn两两互素 //但是如果不是两两互素的话,那么就需要扩展中国剩余定理 //https://www.cnblogs.com/zwfymqz/p/8425731.html LL n; //x=c1(mod m1) LL c[maxn],m[maxn],x,y; LL gcd(LL a,LL b){ if(b==0) return a; return gcd(b,a%b); } LL extend_gcd(LL a,LL b,LL &x,LL &y){ //不仅算了一元二次方程的解,还算出来了公约数 if(b==0){ x=1;y=0;return a; } LL r=extend_gcd(b,a%b,x,y); LL tmp=x; x=y; y=tmp-(a/b)*y; return r; } LL inv(LL a,LL b){ //a在模b下的逆 LL r=extend_gcd(a,b,x,y); //最大公约数 while(x<0) x+=b; //取最小非负的逆 return x; } int main(){ while(~scanf("%lld",&n)){ for(int i=1;i<=n;i++){ scanf("%lld %lld",&m[i],&c[i]); } bool flag=0; for(int i=2;i<=n;i++){ //两两合并位1个,并继续扩展 LL m1=m[i-1],m2=m[i]; LL c1=c[i-1],c2=c[i]; LL t=gcd(m1,m2); if((c2-c1)%t!=0){ flag=1;break; //必须余数为0 因为式子中要出现相除 } m[i]=(m1*m2)/t; c[i]=(inv(m1/t,m2/t)*(c2-c1)/t)%(m2/t)*m1+c1; c[i]=(c[i]%m[i]+m[i])%m[i]; //还有这一步,别忘了 } printf("%lld\n",flag? -1:c[n]); } return 0; }
3.6 质因子分解
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;
const int maxn=100010;
bool is_prime(int x){
if(x==1) return 0;
for(int i=2;i*i<=x;i++){
if(x%i==0) return 0;
}
return 1;
}
//2147483646
int prime[maxn],ans=0;
struct node{
int x,num; //用结构体存
}fac[10]; //10个就够了
void find_prime(){ //求素数表
for(int i=1;i<maxn;i++){
if(is_prime(i)) prime[ans++]=i;
}
}
int main(){
find_prime();
int n,num=0;
cin>>n;
if(n==1) {
cout<<"1"<<endl;
return 0; //特判
}
cout<<n<<"=";
int sqr=(int)(sqrt(1.0*n));
for(int i=0;prime[i]<=sqr&&i<ans;i++){
if(n%prime[i]==0){
fac[num].x=prime[i];
fac[num].num=0;
while(n%prime[i]==0){
fac[num].num++;
n/=prime[i];
}
num++;
}
if(n==1) break; //提前退出
}
if(n!=1){ //最后不等于1 ,说明有一个大于sqrt(n)的因子
fac[num].x=n;
fac[num++].num=1;
}
for(int i=0;i<num;i++){
if(i>0) cout<<"*";
cout<<fac[i].x;
if(fac[i].num!=1) cout<<"^"<<fac[i].num;
}
return 0;
}
ps.如果进行因子分解后,得到各因子的个数位e1,e2...ek,那么因子个数就是(e1+1)*(e2+1)*...*(ek+1)
因子之和就是(1+p1+p1^2+...+p1^e1)*(1+p2+p2^2+...p2^e2)*...*(1+pk+pk^2+...+pk^ek)
3.7 关于n!的问题
1、求n!中有多少个质因子p
可以枚举,但是很慢
n!中有(n/p+n/p^2+.....)个质因子p.
eg.10!中有5个2^1,2个2^2,1个2^3,所以质因子2的个数位5+2+1=8个,O(logN)
int cal(int n,int p){
int ans=0;
while(n){
ans+=n/p;
n/=p;
}
return ans;
}
应用:计算n!的末尾有几个0,末尾0的个数等于n!中因子10的个数,等于质因子5的个数,计算cal(n,5)就可以了
递归版本:
int cal(int n,int p){
if(n<p) return 0;
return n/p+cal(n/p,p);
}
高次同余方程 BSGS

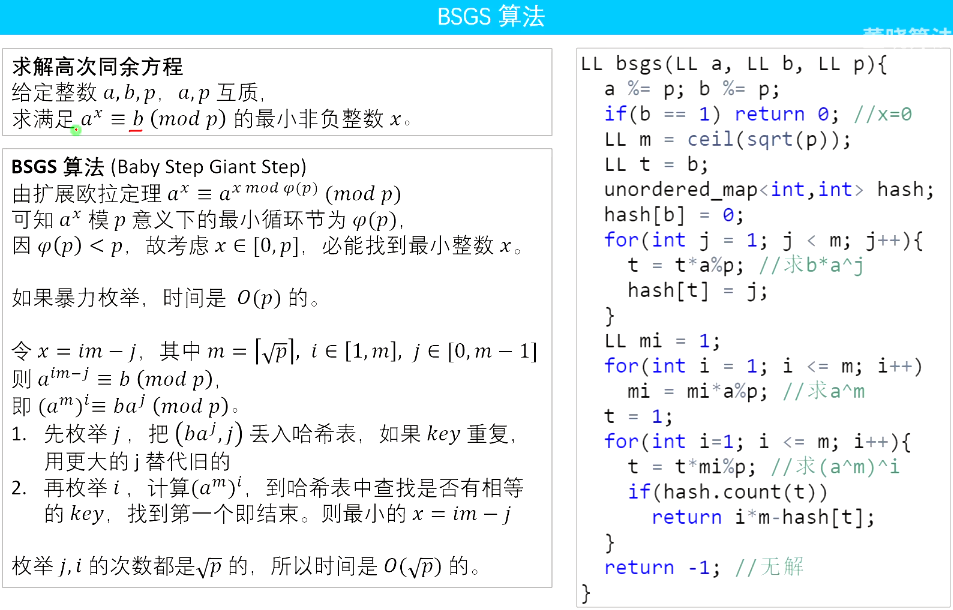
https://www.luogu.com.cn/problem/P3846 P3846 [TJOI2007] 可爱的质数/【模板】BSGS
#include<iostream>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <map>
typedef long long LL;
using namespace std;
LL bsgs(LL a,LL b,LL p){
a%=p;
b%=p;
if(b==1) return 0; //x=0
LL m=ceil(sqrt(p));
LL t=b;
map<int,int> hash;
hash[b]=0;
for(int j=1;j<m;j++){
t=t*a%p;
hash[t]=j;
}
LL mi=1;
for(int i=1;i<=m;i++) mi=mi*a%p;//求a^m
t=1;
for(int i=1;i<=m;i++){
t=t*mi%p;
if(hash.count(t)) return i*m-hash[t];
}
return -1;
}
int main(){
int a,p,b;
cin>>p>>a>>b;
int res=bsgs(a,b,p);
if(res==-1) cout<<"no solution"<<endl;
else cout<<res<<endl;
return 0;
}
扩展BSGS算法:没有a、p互质的条件了,要想办法把他们变得互质


https://www.luogu.com.cn/problem/P4195 P4195 【模板】扩展 BSGS/exBSGS
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#include<map>
using namespace std;
typedef long long LL;
LL gcd(LL a,LL b){
return b==0?a:gcd(b,a%b);
}
LL exbsgs(LL a,LL b,LL p){
a%=p;b%=p;
if(b==1||p==1) return 0; //x=0
LL d,k=0,A=1;
while(1){
d=gcd(a,p);
if(d==1) break;
if(b%d) return -1; //无解,转化为线性方程
k++;
b/=d;p/=d;
A=A*(a/d)%p;
if(A==b) return k; //0次方
}
LL m=ceil(sqrt(p));
LL t=b;
map<int,int> hash;
hash[b]=0;
for(int j=1;j<m;j++){
t=t*a%p;//求b*a^j
hash[t]=j;
}
LL mi=1;
for(int i=1;i<=m;i++){
mi=mi*a%p; //求(a^m)
}
t=A;
for(int i=1;i<=m;i++){
t=t*mi%p; //求(a^m)^i
if(hash.count(t)) return i*m-hash[t]+k;
}
return -1; //无解
}
int main(){
LL a,p,b;
while((scanf("%lld%lld%lld",&a,&p,&b)!=EOF)&&a){
LL res=exbsgs(a,b,p);
if(res==-1) printf("No Solution\n");
else printf("%lld\n",res);
}
return 0;
}



 posted on
posted on

 浙公网安备 33010602011771号
浙公网安备 33010602011771号