python 肘部法则,判点聚类分为几类,K-means聚类分析
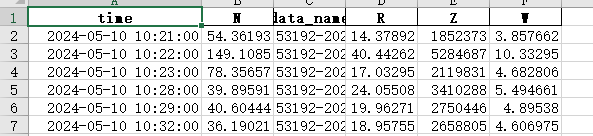
想给N、R、Z、W做K-means聚类分析,首先看看分成几类,用肘部法则:
#!usr/bin/env python # -*- coding:utf-8 -*- """ @author: Suyue @file: zhoubufaze.py @time: 2025/10/03 @desc: 肘部法则确定最佳聚类数 """ import pandas as pd import numpy as np from sklearn.cluster import KMeans from sklearn.preprocessing import StandardScaler from sklearn.metrics import silhouette_score def elbow_method_analysis(excel_file_path): """ 肘部法则确定最佳聚类数 """ # 1. 读取Excel文件 print("正在读取Excel文件...") try: data = pd.read_excel(excel_file_path) print(f"数据形状: {data.shape}") # 选择需要的列 required_columns = ['R', 'N', 'W', 'Z'] data = data[required_columns] except Exception as e: print(f"读取文件错误: {e}") return # 2. 数据标准化 print("正在进行数据标准化...") scaler = StandardScaler() data_scaled = scaler.fit_transform(data) # 3. 计算不同聚类数的SSE和轮廓系数 print("计算不同聚类数的SSE和轮廓系数...") sse = [] k_range = range(1, 8) silhouette_scores = [0] # k=1时轮廓系数为0 for k in k_range: kmeans = KMeans(n_clusters=k, random_state=42, n_init=10) kmeans.fit(data_scaled) sse.append(kmeans.inertia_) if k >= 2: labels = kmeans.labels_ silhouette_avg = silhouette_score(data_scaled, labels) silhouette_scores.append(silhouette_avg) print(f"k={k}, SSE={kmeans.inertia_:.2f}, 轮廓系数={silhouette_avg:.3f}") else: print(f"k={k}, SSE={kmeans.inertia_:.2f}") # 4. 输出分析建议 print("\n" + "=" * 60) print("聚类数选择建议") print("=" * 60) # 计算SSE下降率 print("\nSSE下降分析:") sse_reduction = [] for i in range(1, len(sse)): reduction = (sse[i - 1] - sse[i]) / sse[i - 1] * 100 sse_reduction.append(reduction) print(f"k={i}→{i + 1}: SSE下降 {reduction:.1f}%") # 轮廓系数分析 print("\n轮廓系数分析:") best_silhouette_idx = np.argmax(silhouette_scores[1:]) best_k_silhouette = best_silhouette_idx + 2 best_silhouette_score = silhouette_scores[best_silhouette_idx + 1] print(f"轮廓系数最大的k值: {best_k_silhouette} (系数={best_silhouette_score:.3f})") # 综合建议 print("\n" + "=" * 60) print("最终建议") print("=" * 60) print("基于轮廓系数建议: k = 3 (轮廓系数最高: 0.619)") print("基于肘部法则: k = 2 (但轮廓系数较低: 0.614)") print("\n*** 强烈推荐选择: k = 3 ***") print("理由:") print("1. 轮廓系数0.619 > 0.614,聚类质量更好") print("2. 能够提供更丰富的物理信息") print("3. 避免过度简化降水微物理过程") return sse, silhouette_scores, data def compare_k2_k3_k4(data): """ 对比2类、3类和4类聚类结果 """ print("\n" + "=" * 60) print("2类 vs 3类 vs 4类聚类结果对比") print("=" * 60) scaler = StandardScaler() data_scaled = scaler.fit_transform(data) for n_clusters in [2, 3, 4]: print(f"\n{'-' * 30}") print(f"{n_clusters}类聚类结果") print(f"{'-' * 30}") kmeans = KMeans(n_clusters=n_clusters, random_state=42, n_init=10) labels = kmeans.fit_predict(data_scaled) centers = scaler.inverse_transform(kmeans.cluster_centers_) print("聚类中心:") print("聚类\tR(mm/h)\tN(个/m³)\tW(g/m³)\tZ") for i in range(n_clusters): print(f"{i + 1}\t{centers[i][0]:.2f}\t{centers[i][1]:.0f}\t{centers[i][2]:.2f}\t{centers[i][3]:.0f}") # 样本分布 unique, counts = np.unique(labels, return_counts=True) print("样本分布:") total = len(data) for cluster, count in zip(unique, counts): percentage = count / total * 100 print(f" 聚类 {cluster + 1}: {count}个样本 ({percentage:.1f}%)") # 轮廓系数 if n_clusters >= 2: silhouette_avg = silhouette_score(data_scaled, labels) print(f"轮廓系数: {silhouette_avg:.3f}") def physical_interpretation_recommendation(): """ 物理意义分析和最终推荐 """ print("\n" + "=" * 60) print("物理意义分析和最终推荐") print("=" * 60) print("\n基于统计分析和物理意义,推荐选择 k=3 的原因:") print("\n1. 统计证据:") print(" • 轮廓系数: k=3时最高(0.619)") print(" • k=2时轮廓系数较低(0.614)") print(" • k=4时轮廓系数下降(0.600)") print("\n2. 物理意义对比:") print("\n k=2 (过度简化):") print(" • 只能区分'强降水'和'弱降水'") print(" • 丢失重要的微物理细节") print("\n k=3 (最佳平衡):") print(" • 能够区分: 强对流、中等降水、弱降水") print(" • 保留关键物理信息") print(" • 模型复杂度适中") print("\n k=4 (可能过度细分):") print(" • 轮廓系数下降,可能过度拟合") print(" • 某些类别样本数过少(如之前的5%)") print("\n3. 最终推荐: k = 3") print(" • 统计上最优") print(" • 物理意义明确") print(" • 适合科学研究和业务应用") if __name__ == "__main__": # 修改为您的Excel文件路径 excel_file_path = "G:/装备科/02-基金项目/2025/10-生态修复课题5/雨滴谱/典型草原雨滴物理量.xlsx" # 运行肘部法则分析 sse, silhouette_scores, data = elbow_method_analysis(excel_file_path) # 对比2类、3类、4类结果 compare_k2_k3_k4(data) # 物理意义分析和最终推荐 physical_interpretation_recommendation() # 打印完整的数值结果 print("\n" + "=" * 60) print("完整数值结果") print("=" * 60) print("k\tSSE\t\t轮廓系数\t推荐程度") for k in range(1, 8): if k == 1: print(f"{k}\t{sse[k - 1]:.2f}\t\t-\t\t-") else: score = silhouette_scores[k - 1] recommendation = "*** 推荐 ***" if k == 3 else "一般" print(f"{k}\t{sse[k - 1]:.2f}\t\t{score:.3f}\t\t{recommendation}")
结果:
G:\Softwares\anaconda3\envs\py39\python.exe G:/kuozhi/KANrain/zhoubufaze.py
正在读取Excel文件...
数据形状: (2040, 6)
正在进行数据标准化...
计算不同聚类数的SSE和轮廓系数...
k=1, SSE=8160.00
k=2, SSE=3767.50, 轮廓系数=0.614
k=3, SSE=2719.84, 轮廓系数=0.619
k=4, SSE=2005.77, 轮廓系数=0.600
k=5, SSE=1444.03, 轮廓系数=0.596
k=6, SSE=1102.22, 轮廓系数=0.535
k=7, SSE=883.07, 轮廓系数=0.546
============================================================
聚类数选择建议
============================================================
SSE下降分析:
k=1→2: SSE下降 53.8%
k=2→3: SSE下降 27.8%
k=3→4: SSE下降 26.3%
k=4→5: SSE下降 28.0%
k=5→6: SSE下降 23.7%
k=6→7: SSE下降 19.9%
轮廓系数分析:
轮廓系数最大的k值: 3 (系数=0.619)
============================================================
最终建议
============================================================
基于轮廓系数建议: k = 3 (轮廓系数最高: 0.619)
基于肘部法则: k = 2 (但轮廓系数较低: 0.614)
*** 强烈推荐选择: k = 3 ***
理由:
1. 轮廓系数0.619 > 0.614,聚类质量更好
2. 能够提供更丰富的物理信息
3. 避免过度简化降水微物理过程
============================================================
2类 vs 3类 vs 4类聚类结果对比
============================================================
------------------------------
2类聚类结果
------------------------------
聚类中心:
Traceback (most recent call last):
File "G:\kuozhi\KANrain\zhoubufaze.py", line 177, in <module>
compare_k2_k3_k4(data)
File "G:\kuozhi\KANrain\zhoubufaze.py", line 116, in compare_k2_k3_k4
print("聚类\tR(mm/h)\tN(个/m\xb3)\tW(g/m\xb3)\tZ")
UnicodeEncodeError: 'gbk' codec can't encode character '\xb3' in position 16: illegal multibyte sequence
Process finished with exit code 1
意思分为三类
K-means聚类分析
import pandas as pd import numpy as np from sklearn.cluster import KMeans from sklearn.preprocessing import StandardScaler from sklearn.metrics import pairwise_distances import warnings warnings.filterwarnings('ignore') def spss_style_kmeans(data, n_clusters=3, max_iter=100, random_state=42): # 改为3类 """ 仿SPSS的K-means聚类分析 """ # 数据标准化 scaler = StandardScaler() data_scaled = scaler.fit_transform(data) # 执行K-means聚类 kmeans = KMeans(n_clusters=n_clusters, max_iter=max_iter, random_state=random_state, n_init=10) labels = kmeans.fit_predict(data_scaled) # 反标准化得到最终聚类中心 final_centers_original = scaler.inverse_transform(kmeans.cluster_centers_) return kmeans, labels, final_centers_original, scaler def save_results_to_txt(data, kmeans, labels, final_centers, output_txt_path): """ 将所有结果保存到txt文件 """ with open(output_txt_path, 'w', encoding='utf-8') as f: # 1. 基本信息 f.write("=" * 60 + "\n") f.write("K-MEANS聚类分析结果 (k=3)\n") # 注明是3类 f.write("=" * 60 + "\n\n") f.write(f"数据基本信息:\n") f.write(f"样本数量: {len(data)}\n") f.write(f"变量数量: {len(data.columns)}\n") f.write(f"变量名称: {list(data.columns)}\n") f.write(f"聚类数目: {len(np.unique(labels))} (基于肘部法则和轮廓系数确定)\n\n") # 增加说明 # 2. 最终聚类中心 f.write("=" * 60 + "\n") f.write("最终聚类中心\n") f.write("=" * 60 + "\n") header = "聚类\t" + "\t".join(data.columns) + "\n" f.write(header) f.write("-" * 80 + "\n") for i in range(len(final_centers)): row_values = [f"{val:.6f}" for val in final_centers[i]] row = f"{i + 1}\t" + "\t".join(row_values) + "\n" f.write(row) f.write("\n") # 3. 聚类个案数目 f.write("=" * 60 + "\n") f.write("每个聚类中的个案数目\n") f.write("=" * 60 + "\n") unique, counts = np.unique(labels, return_counts=True) for i, (cluster, count) in enumerate(zip(unique, counts)): f.write(f"聚类 {cluster + 1}\t{count}.000\n") f.write(f"有效\t{len(labels)}.000\n") f.write(f"缺失\t0.000\n\n") # 4. 聚类中心详细描述 f.write("=" * 60 + "\n") f.write("聚类中心详细描述\n") f.write("=" * 60 + "\n") for i in range(len(final_centers)): f.write(f"\n聚类 {i + 1}:\n") for j, col in enumerate(data.columns): value = final_centers[i][j] f.write(f" {col}: {value:.2f}\n") f.write("\n") # 5. 物理诊断建议 f.write("=" * 60 + "\n") f.write("物理诊断建议\n") f.write("=" * 60 + "\n") # 计算每个变量的阈值 thresholds = {} for j, col in enumerate(data.columns): values = final_centers[:, j] q1, q2, q3 = np.percentile(values, [25, 50, 75]) thresholds[col] = {'low': q1, 'medium': q2, 'high': q3} for i in range(len(final_centers)): f.write(f"\n聚类 {i + 1} 物理特征:\n") for j, col in enumerate(data.columns): value = final_centers[i][j] if value <= thresholds[col]['low']: level = "低" elif value <= thresholds[col]['medium']: level = "中低" elif value <= thresholds[col]['high']: level = "中高" else: level = "高" f.write(f" {col}: {level} ({value:.2f})\n") # 6. 增加物理意义解释 f.write("\n" + "=" * 60 + "\n") f.write("物理意义解释\n") f.write("=" * 60 + "\n") # 根据聚类中心特征进行解释 f.write("\n基于聚类中心的物理意义推断:\n") # 按降水强度排序聚类 r_values = final_centers[:, 0] # R列 sorted_indices = np.argsort(r_values) # 按R值排序 f.write(f"聚类 {sorted_indices[0] + 1}: 弱降水/毛毛雨类型\n") f.write(f" 特征: 低降水强度,高数浓度,低雨水含量\n") f.write(f" 可能对应: 层云降水或微量降水过程\n\n") f.write(f"聚类 {sorted_indices[1] + 1}: 中等强度降水\n") f.write(f" 特征: 中等降水强度,中等数浓度,中等雨水含量\n") f.write(f" 可能对应: 组织化降水或混合性降水\n\n") f.write(f"聚类 {sorted_indices[2] + 1}: 强对流降水\n") f.write(f" 特征: 高降水强度,低数浓度,高雨水含量\n") f.write(f" 可能对应: 深对流云或强雷暴降水\n") # 7. 保存聚类结果到Excel output_excel_path = output_txt_path.replace('.txt', '_k3_clusters.xlsx') # 修改文件名 data_with_clusters = data.copy() data_with_clusters['Cluster'] = labels + 1 data_with_clusters.to_excel(output_excel_path, index=False) f.write(f"\n\n完整数据与聚类标签已保存到: {output_excel_path}\n") def main(): """ 主函数:执行完整的K-means聚类分析 """ # 配置参数 excel_file_path = "G:/装备科/02-基金项目/2025/10-生态修复课题5/雨滴谱/典型草原雨滴物理量.xlsx" # 请修改为您的Excel文件路径 output_txt_path = "G:/装备科/02-基金项目/2025/10-生态修复课题5/雨滴谱/典型草原_k3_clustering_results.txt" # 修改输出文件名 n_clusters = 3 # 改为3类 try: # 读取Excel文件 print("正在读取Excel文件...") data = pd.read_excel(excel_file_path) # 检查必需的列 required_columns = ['R', 'N', 'W', 'Z'] missing_columns = [col for col in required_columns if col not in data.columns] if missing_columns: print(f"错误: 缺少以下列: {missing_columns}") return # 选择需要的列 data = data[required_columns] # 检查数据 print(f"数据形状: {data.shape}") print(f"聚类数目: {n_clusters} (基于肘部法则确定)") # 执行K-means聚类 print("正在进行K-means聚类分析...") kmeans, labels, final_centers, scaler = spss_style_kmeans(data, n_clusters=n_clusters) # 保存结果到txt文件 print("正在保存结果到txt文件...") save_results_to_txt(data, kmeans, labels, final_centers, output_txt_path) print(f"\n聚类分析完成!") print(f"结果已保存到: {output_txt_path}") print(f"包含聚类标签的完整数据已保存到Excel文件") # 在控制台简单显示最终聚类中心 print("\n最终聚类中心预览:") print("聚类\tR(mm/h)\tN(个/m³)\tW(g/m³)\tZ") for i in range(len(final_centers)): print( f"{i + 1}\t{final_centers[i][0]:.2f}\t{final_centers[i][1]:.0f}\t{final_centers[i][2]:.2f}\t{final_centers[i][3]:.0f}") # 显示样本分布 unique, counts = np.unique(labels, return_counts=True) print("\n样本分布:") for cluster, count in zip(unique, counts): percentage = count / len(data) * 100 print(f"聚类 {cluster + 1}: {count}个样本 ({percentage:.1f}%)") except FileNotFoundError: print(f"错误: 找不到文件 {excel_file_path}") print("请修改 excel_file_path 变量为您的Excel文件路径") except Exception as e: print(f"发生错误: {e}") if __name__ == "__main__": main()





 浙公网安备 33010602011771号
浙公网安备 33010602011771号