逆序对的数量 | 归并排序

AC.788 逆序对的数量

题目描述

给定一个长度为 \(n\) 的整数数列，请你计算数列中的逆序对的数量。逆序对的定义如下：对于数列的第 \(i\) 个和第 \(j\) 个元素，如果满足 \(i<j\) 且 \(a[i]>a[j]\) ，则其为一个逆序对；否则不是。

输入格式

第一行包含整数 \(n\) ，表示数列的长度。

第二行包含 \(n\) 个整数，表示整个数列。

输出格式

输出一个整数，表示逆序对的个数。

数据范围

\(1≤n≤100000 ， 数列中的元素的取值范围 [1,109] 。\)

输入样例

6
2 3 4 5 6 1

输出样例

5

---

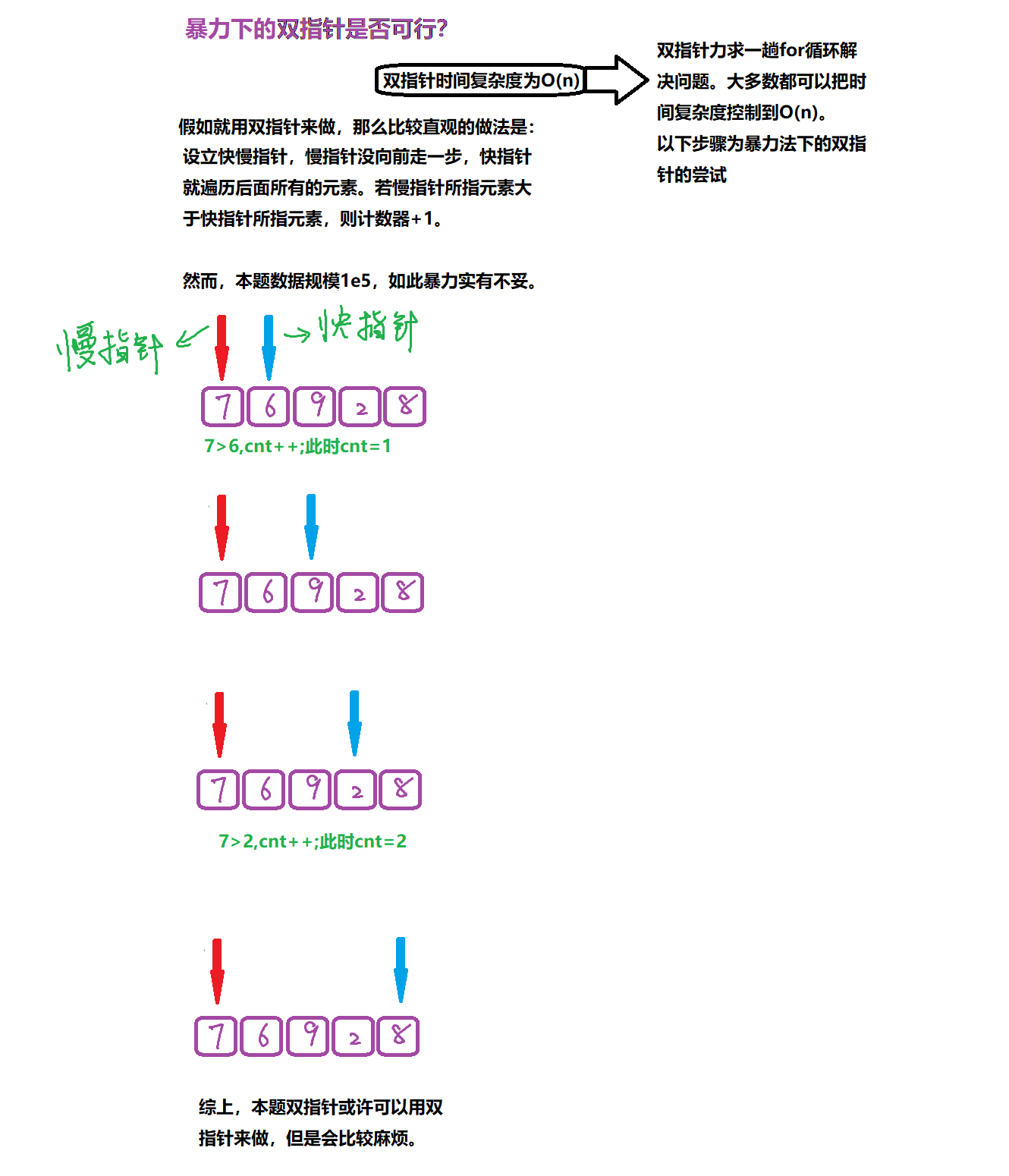
为什么使用归并排序？

• 归并排序时间复杂度为\(O(nlog_2(n))\)，随着数据规模的增大，线性对数级要明显快于平方级
• 归并排序的具体操作中有这样一步：两个指针处理两段区间，谁小就将谁放入临时数组。
• 稳定性 （快排不具有稳定性）

代码

#include<iostream>
using namespace std;
#define ios_base \
	ios::sync_with_stdio(false);\
	cin.tie(nullptr),cout.tie(nullptr)
const int N = 1e5+10;
int a[N],t[N],n;
long long cnt;
long long function(int a[],int l,int r)
{
    if (l>=r) return 0;
    int mid=l+r>>1;
    cnt=function(a,l,mid)+function(a,mid+1,r);
    int i=l,j=mid+1,k=0;
    while (i<=mid && j<=r)
    {
        if (a[i]<=a[j])
        {
            t[k++]=a[i++];
        }else{
            cnt+=mid-i+1;
            t[k++]=a[j++];
        }
        
    }
    while(i<=mid)
    {
        t[k++]=a[i++];
    }
    while(j<=r)
    {
        t[k++]=a[j++];
    }
    for(int t_idx=0,a_idx=l;a_idx<=r;a_idx++,t_idx++)
    {
        a[a_idx]=t[t_idx];
    }
    return cnt;
}
int main()
{
	ios_base;
	cin>>n;
	for (int i = 0; i < n; i++)
	{
		cin>>a[i];
	}
	cout<<function(a,0,n-1)<<'\n';
	
	return 0;
}

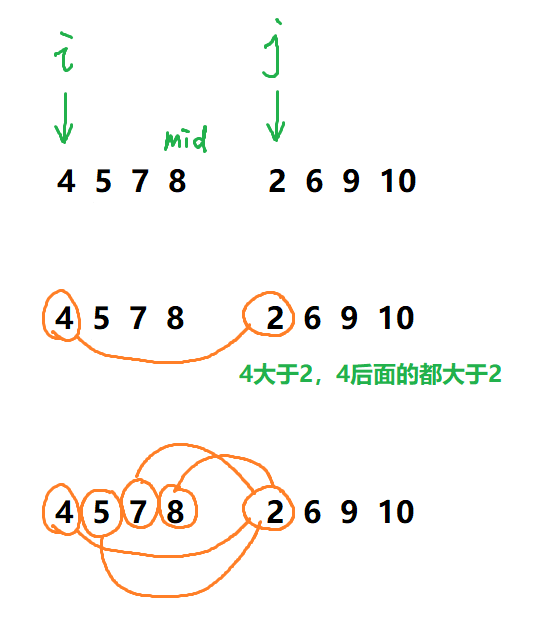
核心代码

res += mid - i + 1;

核心代码秒懂