Convolutional NN

CNN 最早主要用来处理图像信息. 如果用全连接 (fully connected) FNN 来处理, 则会有以下问题:

1. 参数太多: 这会导致训练效率低下, 容易过拟合.
2. 局部不变性特征: 自然图像中的物体都具有局部不变性特征, 比如 scaling, shifting and rotating 都不影响语义信息. 而 FC FNN 很难提取这些特征.

CNN 有三个结构上的特性: local connection, weight sharing and pooling.

CNN 中所谓的 convolution 实际上用的是 cross-correlation, 但是由于考虑的都是有限维的东西, 这两者等价, 后者实现起来更直观容易一些.

用卷积代替全连接

若用卷积代替全连接, 即

\[z^{(l)} = w^{(l)} * a^{(l-1)} + b^{(l)}, \]

其中 \(w\) 称为滤波器 (filter). 根据卷积的定义, 卷积层有两个重要性质:

1. 局部连接. 有原来的 \(n^{(l)}n^{(l-1)}\) 个连接变为 \(n^{(l)}m\) 个连接, 其中 \(m\) 为滤波器维数.
2. 权重共享. \(w^{(l)}\) 是 \(l\) 层所有神经元共享的.

由此, 卷积层的参数只有 \(m\) 维的 \(w\) 和 1 维的 \(b\), 参数个数与神经元数量无关. 另外 \(n^{(l)} = n^{(l-1)} - m + 1\).

卷积层

卷积层的作用是提取一个局部区域的特征, 不同的卷积核相当于不同的特征提取器. 特征映射为一幅图像经过卷积后提取道德特征.

一个卷积层的结构如下:

• 输入特征映射组: \(X\in \mathbb R^{M\times N\times D}\) 为 3 维张量 (tensor), 其中 \(D\) 为深度, 如是 RGB 图像, 则 \(D=3\). 每个切片矩阵 \(X^d\in\mathbb R^{M\times N}\) 为一个输入特征映射.;
• 输出特征映射组: \(Y\in \mathbb R^{M'\times N'\times P}\), 每个切片矩阵 \(Y^p \in \mathbb R^{M'\times N'}\) 为一个输出特征映射;
• 卷积核: \(W\in \mathbb R^{m\times n\times D\times P}\), 其中每个切片矩阵 \(W^{p, d}\in \mathbb R^{m\times n}\) 为一个两维卷积核.

为了计算 \(Y^p\), 用卷积核 \(W^{p,1},\dots, W^{p,D}\) 分别对 \(X^1,\dots X^D\) 进行卷积, 把结果相加, 再加上 bias 得到 \(Z^p\), 激活后得到 \(Y^p\).

\[\begin{align*} Z^p &= W^p * X + b^p = \sum_{d=1}^D W^{p,d}*X^d + b^p,\\ Y^p &= f(Z^p). \end{align*} \]

共需要 \(mnPD + P\) 个参数.

汇聚层

Pooling 其实就是 down sampling 的一种, 作用是减少特征数量.

卷积层虽然可以显著减少连接的数量, 但是神经元个数并没有显著减少. 如果后面接一个分类器, 分类器的输入维数依然很高, 容易过拟合. 为了解决这个问题, 可以在卷积层之后加上一个 pooling layer.

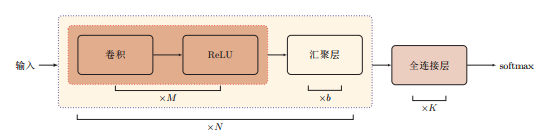
典型的 CNN 结构

\(1\times 1\) Filter

简单地说就是调整维数用的.

One big problem with the above modules, at least in this naive form, is that even a modest number of 5x5 convolutions can be prohibitively expensive on top of a convolutional layer with a large number of filters.
This leads to the second idea of the proposed architecture: judiciously applying dimension reductions and projections wherever the computational requirements would increase too much otherwise. This is based on the success of embeddings: even low dimensional embeddings might contain a lot of information about a relatively large image patch...1x1 convolutions are used to compute reductions before the expensive 3x3 and 5x5 convolutions. Besides being used as reductions, they also include the use of rectified linear activation which makes them dual-purpose. [2]

参数学习

求导比较 trivial, 细节参见 [1], 卷积层的要点是对卷积项的求导, pooling 层的求导可见 [3].

References

[1] 邱锡鹏. (2019). 神经网络与深度学习. https://nndl.github.io/
[2] Indie AI. (2016). What does 1x1 convolution mean in a neural network?. https://stats.stackexchange.com/questions/194142/what-does-1x1-convolution-mean-in-a-neural-network
[3] abora. (2016). Backprop Through Max-Pooling Layers?. https://datascience.stackexchange.com/questions/11699/backprop-through-max-pooling-layers