Binary Tree Traversals

Updated on July 12, 2019

3 Traversal Methods

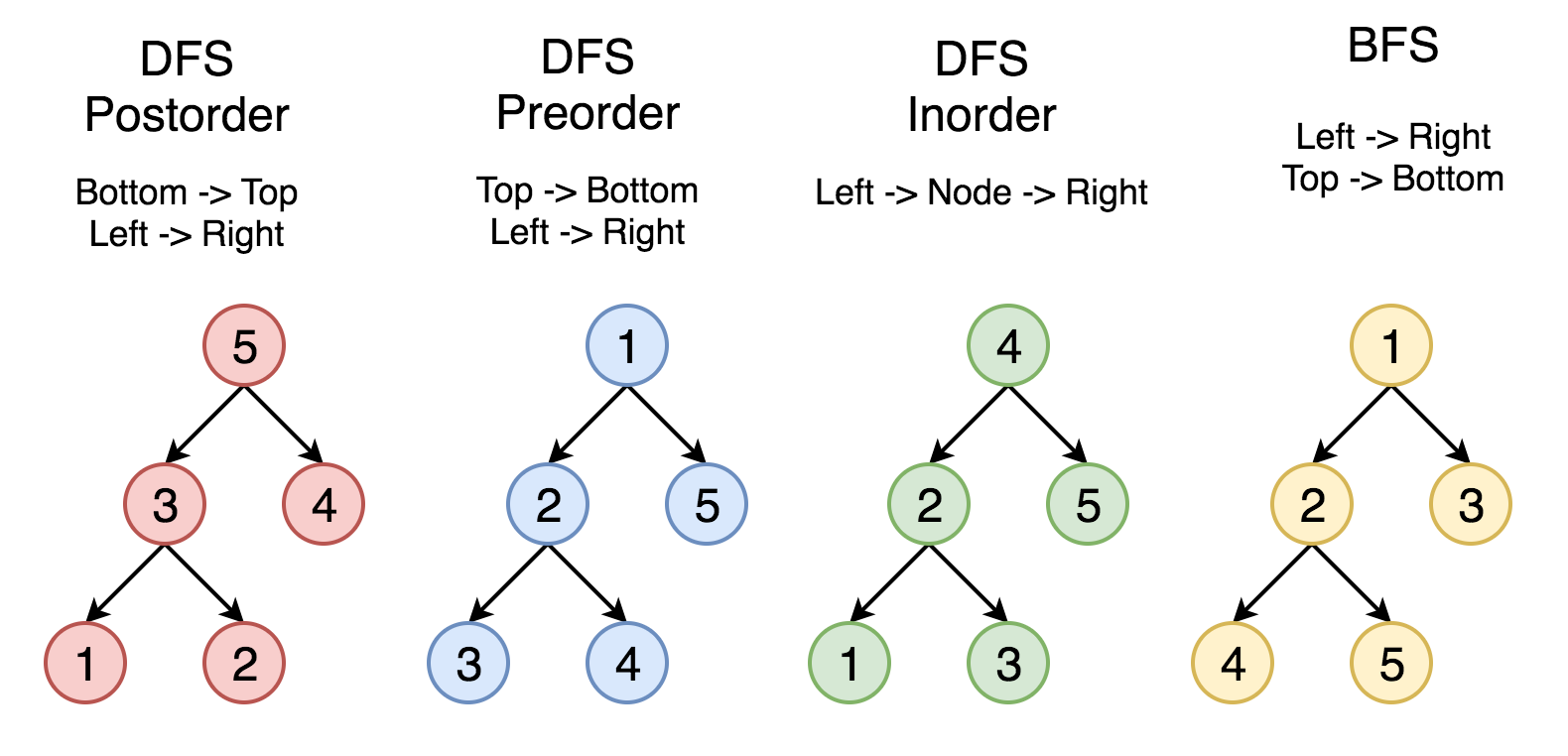
• In pre-order each parent node is visited before (pre) its children.
• In in-order each parent node is visited in between its children.
• In post-order each parent node is visited after (post) its children.

These three terms inorder, preorder and postorder are kept on the order pf processing of ROOT element.
Now when we say INORDER, it means everything is in order i.e. we traverse from left to root to right.
Take an example of a line segment with left end point A and right end point B. Take a mid point M on AB. Now inorder means starting from left (A) going to mid (M) and reaching right (R). As simple as that, everything is in order.
PREORDER means before order. Now what is before? Since i already said the names are kept keeping in mind the root element so the ROOT is before all the elements. So the root will be processed before any element. But remember, the left node will always be processed before right node.
Same goes with POSTORDER. The ROOT element will be processed at last after LEFT and RIGHT nodes have been processed.

From
How did preorder, inorder, and postorder binary tree traversals get their names? - Quora,
How to remember preorder, postorder and inorder traversal - Quora.

Applications

See data structures - When to use Preorder, Postorder, and Inorder Binary Search Tree Traversal strategies - Stack Overflow for applications.

The pic below comes from LeetCode explore card for recursion II.

In-order traversal can be used to solve LeetCode 98. Validate Binary Search Tree.

Python Implementation

Pre-order

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def preorderTraversal(self, root: TreeNode) -> List[int]:
        if not root:
            return []
        stack = [root]
        result = []
        while stack:
            cur = stack.pop()
            result.append(cur.val)
            if cur.right:
                stack.append(cur.right)
            if cur.left:
                stack.append(cur.left)
        return result

In-order

class Solution:
    def inorderTraversal(self, root: TreeNode) -> List[int]:
        stack = []
        result = []
        cur = root
        while stack or cur:
            while cur:
                stack.append(cur)
                cur = cur.left
            cur = stack.pop()
            result.append(cur.val)
            cur = cur.right
        return result

Post-order

'''
This one refers to
https://leetcode.com/problems/binary-tree-postorder-traversal/discuss/45785/Share-my-two-Python-iterative-solutions-post-order-and-modified-preorder-then-reverse
His solution has the same runtime and memory usage as my original code, but is cleaner.
'''
class Solution:
    def postorderTraversal(self, root: TreeNode) -> List[int]:
        stack = [(root, False)]
        result = []
        while stack:
            cur, visited = stack.pop()
            if cur:
                if visited:
                    result.append(cur.val)
                else:
                    stack.append((cur, True))
                    stack.append((cur.right, False))
                    stack.append((cur.left, False))
        return result