PTA 1167 Cartesian Tree (30 分)

1167 Cartesian Tree (30 分)

A Cartesian tree is a binary tree constructed from a sequence of distinct numbers. The tree is heap-ordered, and an inorder traversal returns the original sequence. For example, given the sequence { 8, 15, 3, 4, 1, 5, 12, 10, 18, 6 }, the min-heap Cartesian tree is shown by the figure.

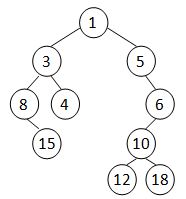
Your job is to output the level-order traversal sequence of the min-heap Cartesian tree.

Input Specification:

Each input file contains one test case. Each case starts from giving a positive integer N (≤30), and then N distinct numbers in the next line, separated by a space. All the numbers are in the range of int.

Output Specification:

For each test case, print in a line the level-order traversal sequence of the min-heap Cartesian tree. All the numbers in a line must be separated by exactly one space, and there must be no extra space at the beginning or the end of the line.

Sample Input:

10
8 15 3 4 1 5 12 10 18 6

Sample Output:

1 3 5 8 4 6 15 10 12 18

感悟

好多人这题拿去建树做,其实没什么必要,bfs遍历一下最小根堆,每次找到当前区间内的最小值,这个最小值就是当前区间的子树的根,用一个数组存下该元素数组下标,并且记下当前的层数,最后用以排序.

#include <iostream>
#include <algorithm>

using namespace std;

typedef pair<int, int> PII;
const int N = 40;
int a[N];
int cnt = 1;
PII b[N];

void find(int l,int r, int level)
{
    if(l>r)return;
    int root = l;
    for(int i = l; i <= r; i++)
        if(a[i] <= a[root]) root = i;
    b[cnt++] = {level,root};
    find(l,root-1,level+1);
    find(root+1,r,level+1);
}

int main()
{
    int n;
    cin >> n;
    for(int i = 1; i <= n; i++)
        cin >> a[i];
    find(1,n,0);
    sort(b+1,b+n+1);
    for(int i = 1; i <= n; i++)
        printf("%d%c",a[b[i].second], i == n ? '\n' : ' ');

    return 0;
}