Monotonic stack to solve leetcode 84: Largest Rectangle in Histogram

Problem:

　　Given n non-negative integers representing the histogram's bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

First let's see an example.

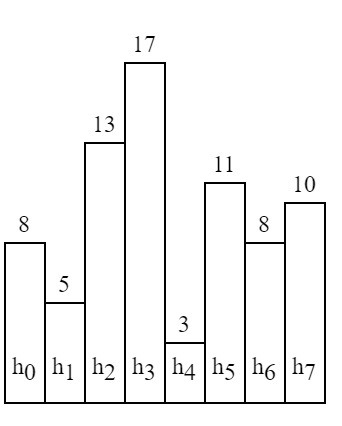
　　　　　　Graph 1

The height of the given histogram is [8,5,13,17,3,11,8,10].

A naive brute force approach is to find the shortest bar between h_i and h_j inclusively, for all 0<=i<=j<length of array. The time complexity would be O(n³). However, we could transform the method to a smarter one: for each histogram bar, what is the largest possible rectangle generated with the height of it? That is, in other words, we start with a rectangle of a single histogram bar, and we try to extend the rectangle leftwards and rightwards as far as possible. What is the barrier of extension?

     

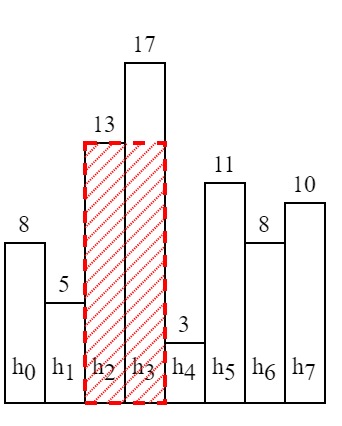
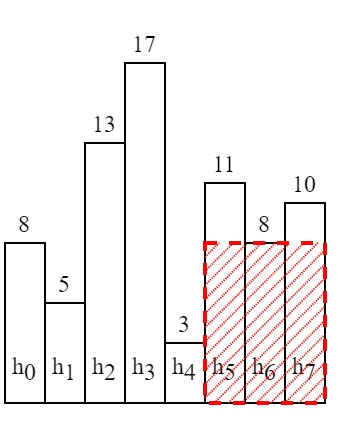
　　　　　　Graph 2　　　　　　　　　　　　　Graph 3

As shown in Graph 2 and Graph 3, the extension stops when we encounter a shorter bar or the boundary of array. The largest rectangle generated with h₂ is filled by red dash, and we can see that we cannot extend it any more because 5 and 3 are all less than 13. Therefore, the question is equal to for each integer in an array, find out the indices of first smaller number to its left (denoted by l) and to its right (denoted by r). The largest rectangle generated with a certain bar has an area of (r-l-1)*h_i. The result we want is max{(r-l-1)*h_i} for all i.

I already issued an article which described a solution to find out the first greater element on the right in an array for all entries. We could apply a similar approach to solve this question. The algorithm is described as follows:

• 1. initiate an int variable res with the value of first number in the array
• 2. go through the array and maintain a strictly monotonically increasing stack, in the stack we store the index instead of height value.
• 3. when we get to index i, if height at i is greater than height of stack top, we push i into the stack, or
• 4. pop out the top of stack, denoted by j, we know that all bars between stack top and i, non-inclusively, are greater or equal to h_j, thus we can calculate the area of largest rectangle generated with jth bar, which is (i-stack.top-1)*h_j, update res if needed. repeat 4 until height of stack top is smaller than h_i, push i onto stack.
• 5. after we iterate over all indices in the array, pop out stack repeatedly. each time we perform a pop operation, denote the popped out value by j, we know that all bars from stack top+1 to end of array inclusively is greater or each to h_j. compute (array.length-stack.top-1)*h_j, update res if necessary.

code is shown below:

public int largestRectangleArea(int[] heights) {
    if(heights.length==0)return 0;
    int res=heights[0];
    Stack<Integer> s=new Stack<Integer>();
    s.push(-1);
    for(int i=0;i<heights.length;i++){
        while(s.peek()!=-1 && heights[s.peek()]>=heights[i]){
            int j=s.pop();
            res=Math.max(res,heights[j]*(i-s.peek()-1));
        }
        s.push(i);
    }
    while(s.peek()!=-1){
        int j=s.pop();
        res=Math.max(res,heights[j]*(heights.length-s.peek()-1));
    }
    return res;
}