PageRank| 图论与推荐系统

1. PageRank

数据之中蕴藏着关系，如果数据量足够大，这种关系越逼近真实世界的客观规律。在我们的工作和生活中你会发现，网页之间的链接关系蕴藏着网页的重要性排序关系，购物车的商品清单蕴藏着商品的

关联关系，通过对这些关系的挖掘，可以帮助我们更清晰地了解客观世界的规律，并利用规律提高生产效率，进一步改造我们的世界。挖掘数据的典型应用场景有搜索排序、关联分析以及聚类；

我们使用 Google 进行搜索的时候，你会发现，通常在搜索的前三个结果里就能找到自己想要的网页内容，而且很大概率第一个结果就是我们想要的网页。而排名越往后，搜索结果与我期望的偏差越大。

并且在搜索结果页的上面，会提示总共找到多少个结果。那么 Google 为什么能在十几万的网页中知道我最想看的网页是哪些，然后把这些页面排到最前面呢？

答案是 Google 使用了一种叫 PageRank 的算法，这种算法根据网页的链接关系给网页打分。如果一个网页 A，包含另一个网页 B 的超链接，那么就认为 A 网页给 B 网页投了一票，以下面四个网页 A、

B、C、D 举例，带箭头的线条表示链接。

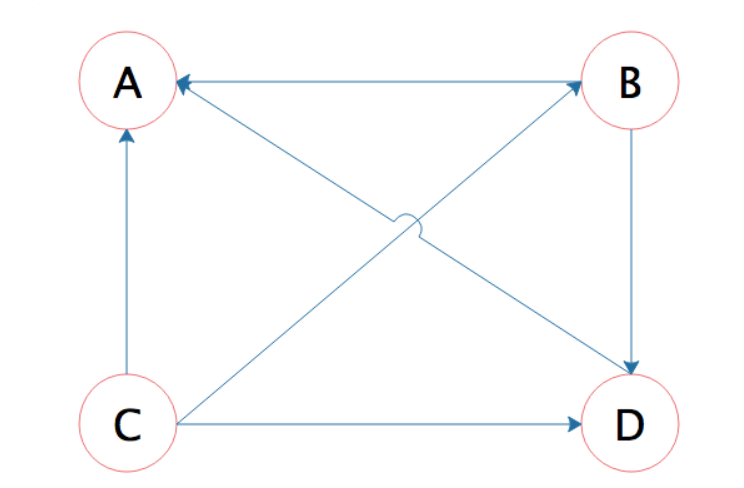
B 网页包含了 A、D 两个页面的超链接，相当于 B 网页给 A、D 每个页面投了一票，初始的时候，所有页面都是 1 分，那么经过这次投票后，B 给了 A 和 D 每个页面 1/2 分（B 包含了 A、D 两个超链

接，所以每个投票值 1/2 分），自己从 C 页面得到 1/3 分（C 包含了 A、B、D 三个页面的超链接，每个投票值 1/3 分）。而 A 页面则从 B、C、D 分别得到 1/2、1/3、1 分。用公式表示就是

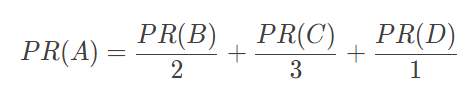
等号左边是经过一次投票后，A 页面的 PageRank 分值；等号右边每一项的分子是包含 A 页面超链接的页面的 PageRank 分值，分母是该页面包含的超链接数目。

这样经过一次计算后，每个页面的 PageRank 分值就会重新分配，重复同样的算法过程，经过几次计算后，根据每个页面 PageRank 分值进行排序，就得到一个页面重要程度的排名表。根据这个排名

表，将用户搜索出来的网页结果排序，排在前面的通常也正是用户想要的结果。

但是这个算法还有个问题，如果某个页面只包含指向自己的超链接，这样的话其他页面不断给它送分，而自己一分不出，随着计算执行次数越多，它的分值也就越高，这显然是不合理的。这种情况就像

下图所示的，A 页面只包含指向自己的超链接。

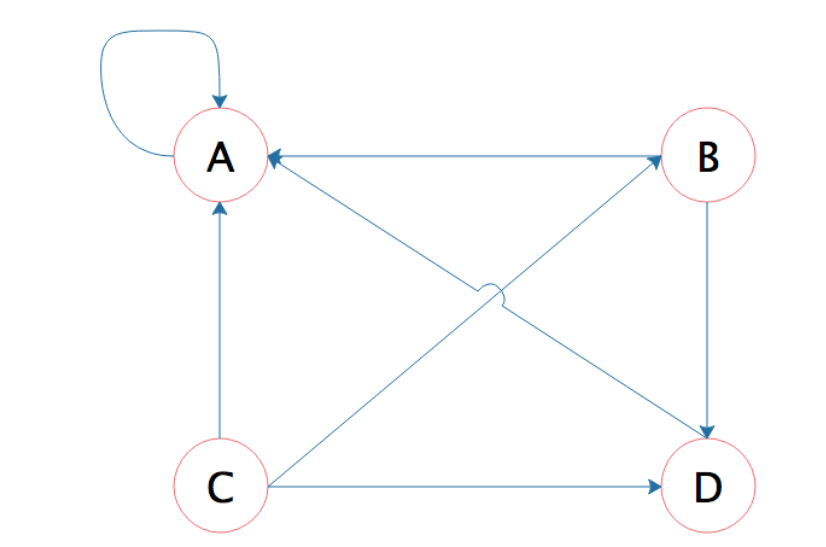
Google 的解决方案是，设想浏览一个页面的时候，有一定概率不是点击超链接，而是在地址栏输入一个 URL 访问其他页面，表示在公式上，就是

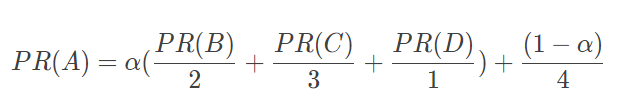
上面（1−α）就是跳转到其他任何页面的概率，通常取经验值 0.15（即 α 为 0.85），因为有一定概率输入的 URL 是自己的，所以加上上面公式最后一项，其中分母 4 表示所有网页的总数。那么对于 N

个网页，任何一个页面 Pi 的 PageRank 计算公式如下：

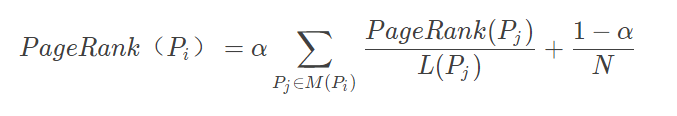
公式中，P_j∈M(P_i) 表示所有包含有 P_i 超链接的 P_j，L(P_j) 表示 P_j 页面包含的超链接数，N 表示所有的网页总和。

由于 Google 要对全世界的网页进行排名，所以这里的 N 可能是一个万亿级的数字，一开始将所有页面的 PageRank 值设为 1，带入上面公式计算，每个页面都得到一个新的 PageRank 值。再把这些新

的 PageRank 值带入上面的公式，继续得到更新的 PageRank 值，如此迭代计算，直到所有页面的 PageRank 值几乎不再有大的变化才停止。

在这样大规模的数据上进行很多次迭代计算，是传统计算方法根本解决不了的问题，这就是 Google 要研发大数据技术的原因，并因此诞生了一个大数据行业。而 PageRank 算法也让 Google 从众多搜索

引擎公司脱颖而出，铸就了 Google 接近万亿级美元的市值，开创了人类科技的新纪元。

什么是PageRank

在PageRank提出之前，搜索引擎面临的问题：

返回结果质量不高
容易被作弊

=> 如何找到优质的网页

匹配用户查找的内容
按照权重排序输出给用户

1998年，Stanford大学博士生Larry Page和Sergey Brin创立了Google，使用PageRank对海量的网页进行重要性分析。

受到论文影响力的启发

图论模型

有向图：边有方向的图，也就是A->B != B->A
无向图：没有方向的图，也就是有向图去掉所有方向
入度：有向图某个顶点作为终点的次数和。
出度：有向图某个顶点作为起点的次数和。
- 入度+出度称之为节点的度

A的出度= 3，入度=2，度= 5 ；

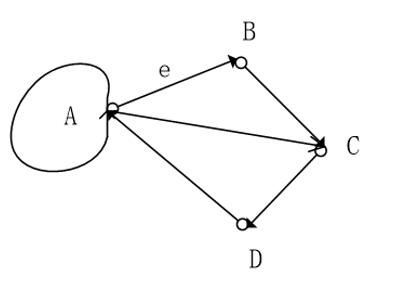
PageRank简化模型

出链：链接出去的链接。

入链：链接进来的链接。

一个网页u的影响力=所有入链集合的页面的加权影响力之和

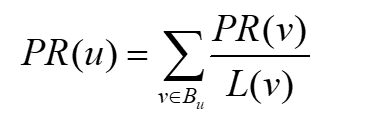
u：待评估的页面，Bu为u的入链集合。

对于Bu中的任意页面v，它能给u带来的影响力是其自身的影响力PR(v)除以v页面的出链数量。即页面v把影响力PR(v)平均分配给了它的出链。这样统计所有能给u带来链接的页面v，得到的总和即为u的

影响力，即为PR(u)。

如果图所示，A的票来自B和C，L(v)为链接出去边的个数；PR(A) = PR(B) / 2 + PR(C) / 1 ； C手中的票100%都给了A，B手中的票一半给了A、一半给了B；

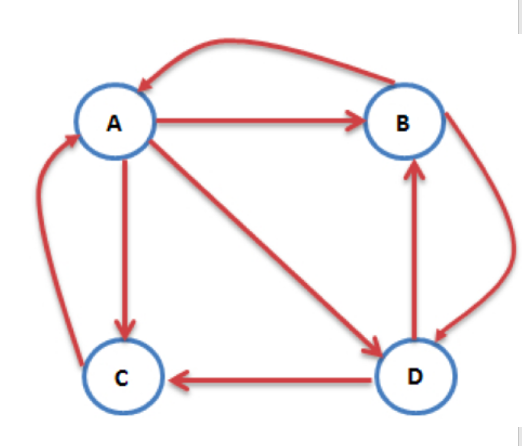
转移矩阵

转移矩阵：统计网页对于其他网页的跳转概率；

原因：出链会给被链接的页面赋予影响力，关键在于统计他们出链的数量；

顶点A走向了B、C、D，所以都占1/3；顶点B走向了A、D，所以各占1/2；顶点C走向了A，占1；顶点D走向了B、C，各占1/2；

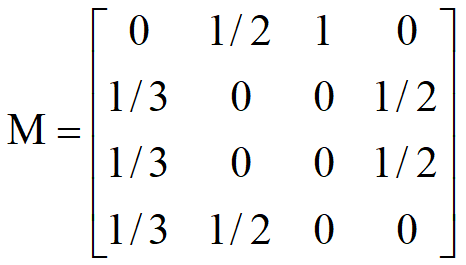
转移矩阵可以帮助我们推导每一时刻影响力的变化；

PageRank过程推导：

Step1，假设A、B、C、D的初始影响力相同W₀ ；

Step2，进行第一次转移之后，页面的影响力变为

Step3，进行n次迭代后，直到页面的影响力不再发生变化，也就是页面的影响力收敛=>最终的影响力

PageRank的代码推导：
import numpy as np
a = np.array([[0, 1/2, 1, 0], 
          [1/3, 0, 0, 1/2],
          [1/3, 0, 0, 1/2],
          [1/3, 1/2, 0, 0]])
b = np.array([1/4, 1/4, 1/4, 1/4])
w = b
for i in range(100):
    w = np.dot(a, w)
    print(w)

简化版的模型在实际应用中是否Work？

Rank Leak（等级泄露）
Rank Sink（等级沉没）

　　不是所有的节点都满足：既有出度，又有入度

Rank Leak（等级泄露）

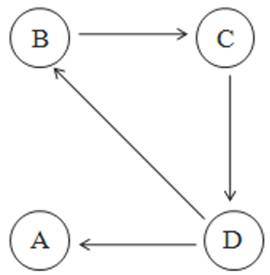
一个网页没有出链，就像是一个黑洞一样，吸收了别人的影响力而不释放，最终会导致其他网页的PR值为0

只进不出，比如下图的A，最终会导致除了A以外其他网页的影响力都是0；

Rank Sink（等级沉没）

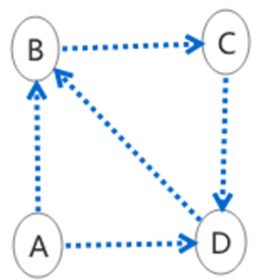
一个网页只有出链，没有入链。比如节点A

迭代下来，会导致这个网页的PR值为0

只出不进，像雷锋样的人物；则A的影响力为0；

在简化模型上处理Rank Leak和Rank Sink

比如针对Rank Leak，把没有出链的节点，先从图中去掉，等所有节点计算完Rank值之后，再加上该节点进行计算。不过这种方法会导致新的Rank Leak节点的产生。

=> 治标不治本

PageRank的随机浏览模型

Larry Page提出了PageRank的随机浏览模型

假设场景：用户并不都是按照跳转链接的方式来上网，还有一种可能是不论当前处于哪个页面，都有概率访问到其他任意的页面

引入阻尼因子：d 通常取值为0.85（默认）（如果d=1就没有随机浏览了就变成经典模型了，d=0是只有随机；适当调整对模型影响不大）

即之前的简化版模型 * d阻尼因子，（85%情况走简化版模型），+ 随机浏览（15%情况）

使用随机浏览模型进行Python模拟
def random_work(a, w, n):
    d = 0.85
    for i in range(100):
        w = (1-d)/n + d*np.dot(a, w)
        print(w)


解决了Rank Leak和Rank Sink问题
和简化模型结果略有不同，但影响力排序没有变化

PageRank的影响力和工具的使用

社交网络领域

如何计算博主影响力（粉丝数=影响力么？）
如何计算职场影响力（脉脉的影响力计算）

生物领域：

基因、蛋白研究，通过PageRank确定七个与遗传有关的肿瘤基因

推荐系统：

用户行为转化为图的形式
对用户u进行推荐，转化为计算用户u和与所有物品i之间的相关性，取与用户没有直接边相连的物品，按照相关性的高低生成推荐列表

交通网络

预测城市的交通流量和人流动向

PageRank工具使用

igraph：处理复杂网络问题，提供Python, R, C语言接口，性能强大，效率比NetworkX高
NetworkX：基于python的复杂网络库，对于Python使用者友好

图的构造，顶点和边 <node, edge>

import networkx as nx
# 创建有向图
G = nx.DiGraph() 
# 有向图之间边的关系
edges = [("A", "B"), ("A", "C"), ("A", "D"), ("B", "A"), ("B", "D"), ("C", "A"), ("D", "B"), ("D", "C")]
for edge in edges:
    G.add_edge(edge[0], edge[1])
pagerank_list = nx.pagerank(G, alpha=1) #alpha=1简化版模型 
print("pagerank值是：", pagerank_list)

import networkx as nx
图的创建
无向图，使用nx.Graph()来创建
有向图，使用nx.DiGraph()来创建
节点的增加、删除和查询
添加节点：使用G.add_node('A')，也可以使用G.add_nodes_from(['B','C','D','E'])
删除节点：使用G.remove_node(node)，也可以使用G.remove_nodes_from(['B','C','D','E'])


节点查询：G.nodes()获取图中所有节点，G.number_of_nodes()获取图中节点的个数。

边的增加
G.add_edge("A", "B")添加指定的从A到B的边
G.add_edges_from 从边集合中添加
G.add_weighted_edges_from 从带有权重的边的集合中添加
参数为1个或多个三元组[u,v,w]作为参数，u、v、w分别代表起点、终点和权重
边的删除
G.remove_edge，G.remove_edges_from


边的查询
G.edges()获取图中所有边，G.number_of_edges()获取图中边的个数。

import networkx as nx
import matplotlib.pyplot as plt
# 创建有向图
G = nx.DiGraph()   
# 设置有向图的边集合
edges = [("A", "B"), ("A", "C"), ("A", "D"), ("B", "A"), ("B", "D"), ("C", "A"), ("D", "B"), ("D", "C")]
# 在有向图G中添加边集合
for edge in edges:
    G.add_edge(edge[0], edge[1])

# 有向图可视化
layout = nx.spring_layout(G)
nx.draw(G, pos=layout, with_labels=True, hold=False)
plt.show()
# 计算简化模型的PR值
pr = nx.pagerank(G, alpha=1)
print("简化模型的PR值：", pr)
# 计算随机模型的PR值
pr = nx.pagerank(G, alpha=0.8)
print("随机模型的PR值：", pr)

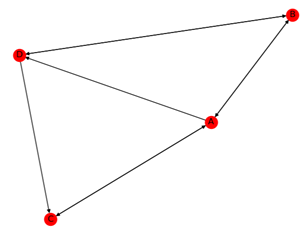
NetworkX的可视化布局：

spring_layout：中心放射状

circular_layout：在一个圆环上均匀分布节点

random_layout：随机分布节点

shell_layout：节点都在同心圆上

使用PageRank分析邮件中的人物关系及影响力

数据集：https://github.com/cystanford/PageRank（希拉里邮件丑闻）

包括了9306封邮件和513个人名

Emails.csv：记录了所有公开邮件的内容，发送者和接受者的信息。

Persons.csv：统计了邮件中所有人物的姓名及对应的ID。

Aliases.csv：因为姓名存在别名的情况，为了将邮件中的人物进行统一，我们还需要用Aliases文件来查询别名和人物的对应关系。

# 数据加载
emails = pd.read_csv("./input/Emails.csv")
# 读取别名文件
file = pd.read_csv("./input/Aliases.csv")
aliases = {}
for index, row in file.iterrows():
    aliases[row['Alias']] = row['PersonId']
# 读取人名文件
file = pd.read_csv("./input/Persons.csv")
persons = {}
for index, row in file.iterrows():
    persons[row['Id']] = row['Name']


# 针对别名进行转换        
def unify_name(name):
# 画网络图
def show_graph(graph):
# 将寄件人和收件人的姓名进行规范化
emails.MetadataFrom = emails.MetadataFrom.apply(unify_name)
emails.MetadataTo = emails.MetadataTo.apply(unify_name)
# 设置遍的权重等于发邮件的次数
edges_weights_temp = defaultdict(list)




for row in zip(emails.MetadataFrom, emails.MetadataTo, emails.RawText):
    temp = (row[0], row[1])
    if temp not in edges_weights_temp:
        edges_weights_temp[temp] = 1
    else:
        edges_weights_temp[temp] = edges_weights_temp[temp] + 1
# 转化格式 (from, to), weight => from, to, weight
edges_weights = [(key[0], key[1], val) for key, val in edges_weights_temp.items()]



# 创建一个有向图
graph = nx.DiGraph()
# 设置有向图中的路径及权重(from, to, weight)
graph.add_weighted_edges_from(edges_weights)
# 计算每个节点（人）的PR值，并作为节点的pagerank属性
pagerank = nx.pagerank(graph)
# 获取每个节点的pagerank数值
pagerank_list = {node: rank for node, rank in pagerank.items()}
# 将pagerank数值作为节点的属性
nx.set_node_attributes(graph, name = 'pagerank', values=pagerank_list)
# 画网络图
show_graph(graph)



# 将完整的图谱进行精简
# 设置PR值的阈值，筛选大于阈值的重要核心节点
pagerank_threshold = 0.005
# 复制一份计算好的网络图
small_graph = graph.copy()
# 剪掉PR值小于pagerank_threshold的节点
for n, p_rank in graph.nodes(data=True):
    if p_rank['pagerank'] < pagerank_threshold: 
        small_graph.remove_node(n)
# 画网络图
show_graph(small_graph, 'circular_layout')

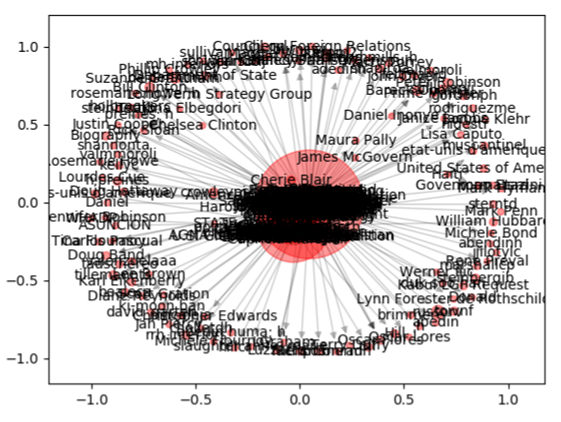
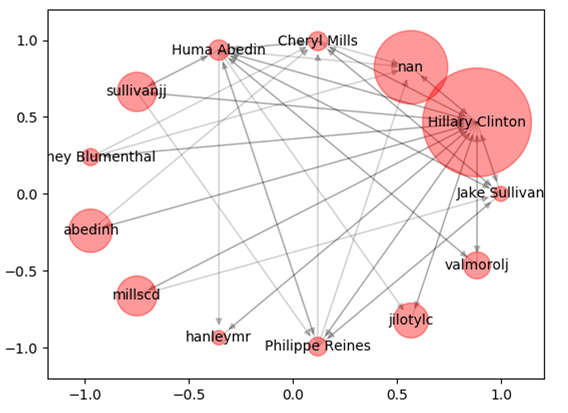
PageRank相关算法

PageRank不仅仅是一种算法，而是一种思想；

TextRank算法

EdgeRank算法

PersonalRank算法

TextRank算法

一种用于文本的基于图的排序算法
根据词之间的共现关系构造网络
构造的网络中的边是无向有权边

对下面句子进行分词得到如图所示：

Compatibility of systems of linear constraints over the set of natural numbers. Criteria of compatibility of a system of linear Diophantine equations, strict inequations, and nonstrict inequations are

considered. Upper bounds for components of a minimal set of solutions and algorithms of construction of minimal generating sets of solutions for all types of systems are given. These criteria and the

corresponding algorithms for constructing a minimal supporting set of solutions can be used in solving all the considered types systems and systems of mixed types.

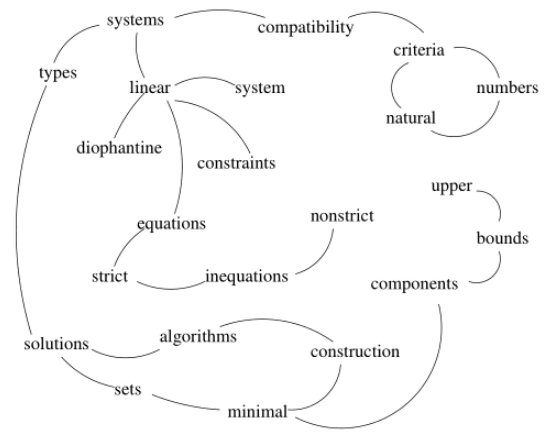
什么是分词和词性

文本：土耳其国防部9日晚宣布，土军队已对叙利亚北部的库尔德武装展开军事行动。
进行分词：seg_list = jieba.cut(sentence, cut_all=False)
获取词性：words = pseg.cut(sentence)

都有哪些词性：

文本：土耳其国防部9日晚宣布，土军队已对叙利亚北部的库尔德武装展开军事行动。

进行分词：seg_list = jieba.cut(sentence, cut_all=False)

获取词性：words = pseg.cut(sentence)

TextRank流程

Step1，进行分词和词性标注，将单词添加到图中

Step2，出现在一个窗口中的词形成一条边

Step3，基于PageRank原理进行迭代（20-30次）

Step4，顶点（词）按照分数进行排序，可以筛选指定的词性

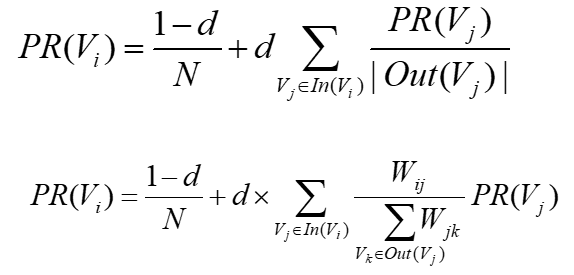
Wij: 单词i和j之间的权重

节点的权重不仅依赖于入度，还依赖于入度节点的权重

jieba中使用TextRank提取关键词

jieba.analyse.textrank(string, topK=20, withWeight=True, allowPOS=())
string：待处理语句
topK：输出topK个词，默认20
withWeight：是否返回权重值，默认false
allowPOS：是否仅返回指定类型，默认为空

jieba中使用TF-IDF提取关键词

jieba.analyse.extract_tags(sentence, topK=20, withWeight=True, allowPOS=())
效果好于TextRank，考虑了IDF的情况，而TextRank倾向使用频繁词
效率高于TextRank，TextRank基于图的计算和迭代较慢

textrank4zh工具

TextRank除了可以找到关键词，还可以生成摘要（关键句子）
依赖分词，分词提取结果及TextRank结果与jieba存在差异

from textrank4zh import TextRank4Keyword, TextRank4Sentence
# 输出关键词，设置文本小写，窗口为2
tr4w = TextRank4Keyword()
tr4w.analyze(text=text, lower=True, window=2)
print('关键词：')
for item in tr4w.get_keywords(20, word_min_len=1):
    print(item.word, item.weight)


# 输出重要的句子
tr4s = TextRank4Sentence()
tr4s.analyze(text=text, lower=True, source = 'all_filters')
print('摘要：')
# 重要性较高的三个句子
for item in tr4s.get_key_sentences(num=3):
    # index是语句在文本中位置，weight表示权重
    print(item.index, item.weight, item.sentence)

TextRank生成摘要的原理：

每个句子作为图中的节点
如果两个句子相似，则节点之间存在一条无向有权边
相似度=同时出现在两个句子中的单词的个数/句子中单词个数求对数之和
- （分母使用对数可以降低长句在相似度计算上的优势）

EdgeRank

2017年底，微博采用了类似FaceBook的EdgeRank算法。

权重高低按：

粉丝亲密度
内容质量
原创程度等来区分

结果：微博算法调整，100万真实粉丝的账号，阅读量不到10万

基于图的推荐算法

将用户行为转化为图模型

哪些不与用户u相连的item节点，对用户u的影响力大？

黑色点代表用户，a/b/c/d/e代表商品item；

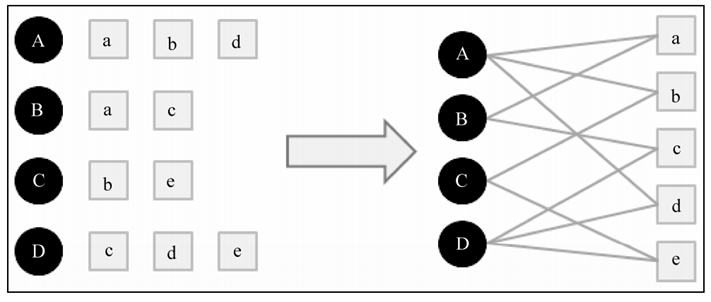
从用户u对应的节点开始游走

PageRank随机模型改成以(1-d)的概率固定从u重新开始

d的概率继续游走

当收敛的时候，计算item节点影响力排名，即为用户u感兴趣的item

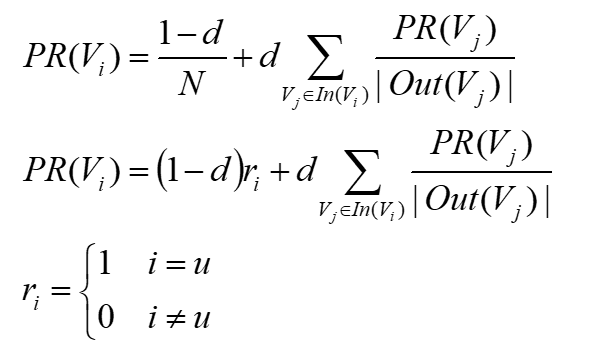
Summary

经典的模型往往很简单，但影响力巨大
可以衍生出很多相关/改进模型
PageRank提出了一个经典的基于图论的影响力模型

如何将工程转化为模型

关联性：能否转化为图论，类似Word Embedding中的word和sentence
需求点：影响力排序，item embedding 相似度计算

2. 图论

图论工具的作用

如果我们把图看成工具的话，它可以满足我们很多需求

节点影响力：PageRank
社区发现：LPA
最短路径：Dijkstra，Floyd

节点可以是任何事物：words, sentences, images, users

什么是社区发现

现实中存在着各种网络：社交网络，交通网络，交易网络，食物链。将这些行为转化为图的网络形式

社区发现是一种聚类算法

作用：精准定位群体，方便进行商品推荐，好友推荐，广告投放

机器学习的三种形式

监督学习：利用已经标注好的数据样本，训练模型
无监督学习：数据都没有标注，利用没有标注的样本进行类别划分，也称为聚类。
半监督学习：介于监督学习和无监督学习之间。同时使用标记数据和未标记数据的机器学习方法。原理是：基于数据分布上的模型假设，利用少量的已标注数据进行指导并预测未标记数据的标记，并合并到标记数据集中。LPA标签传播算法属于半监督学习。

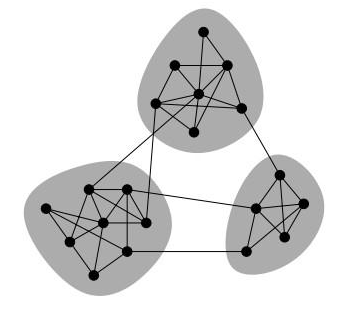
社区的种类

非重叠社区：任意两个社区的顶点之间没有交集
重叠社区，在社区内部存在顶点之间的交集

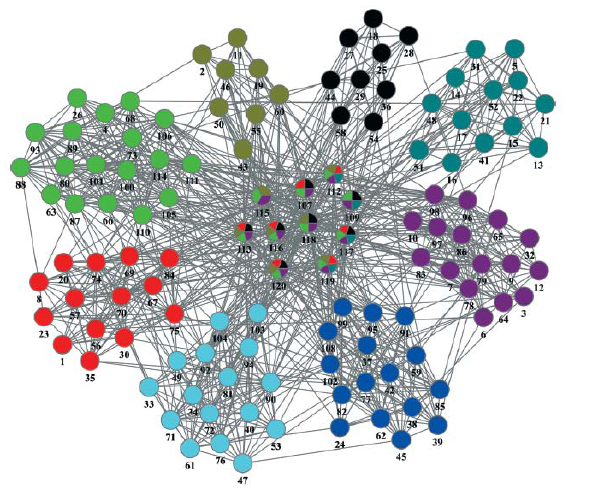
社区发现常用算法LPA& COPRA

LPA：Label Propagation Algorithm 非重叠社区，基于标签传播的非重叠社区发现算法
COPRA：Community Overlap PRopagation Algorithm，基于LPA的扩展算法，用于重叠社区发现算法

LPA算法

Step1，每个节点拥有独立的标签
Step2，标签传播，节点向邻居节点传播自己的标签
Step3，标签更新，每个节点的标签更新为邻居节点中出现次数最多的标签。如果存在多个选择，则随机选择一个
Step4，如果节点更新后的标签发生了变化，则返回到Step2（激活状态），否则节点进入非激活状态，如果所有图中所有节点均为非激活状态，则标签更新结束。此时具有相同标签的节点属于同一个社区

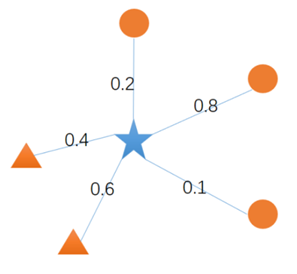
LPA算法示意

使用加权和更新节点标签
- 圆形标签权重=0.2+0.8+0.1=1.1
- 三角形标签权重=0.4+0.6=1，所以节点标签更新为圆形
使用加权平均更新节点标签
- 圆形标签权重=(0.2+0.8+0.1)/3=0.367
- 三角形标签权重=(0.4+0.6)/2=0.5，节点标签更新为三角形

图论工具NetWorkX & igraph

图论工具NetworkX
G=nx.read_gml('./football.gml')
nx.draw(G,with_labels=True) 
plt.show() 
print(nx.shortest_path(G, source='Buffalo', target='Kent'))
print(nx.shortest_path(G, source='Buffalo', target='Rice'))

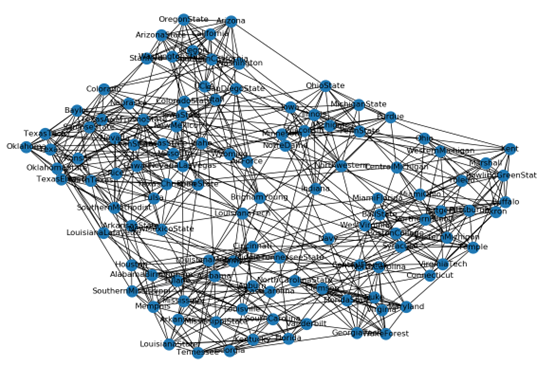
社区发现数据集

football.gml
- 美国大学生足球联赛的复杂网络，包括115支球队（节点）和616场比赛（边）。实际上参赛的115支球队被分为12个联盟。比赛机制为：联盟内部的球队进行小组赛,然后是联盟之间比赛。
karate.gml
- 一个美国大学空手道俱乐部的网络，34个成员（节点）和78条边（成员之间存在的友谊关系）
dolphins.gml
- 长达7年的时间观察新西兰Doubtful Sound海峡 62 只海豚（节点）的交流情况（边）而得到的复杂网络。有 62 个节点，159 条边。

图论工具NetworkX

import networkx as nx
from networkx.algorithms import community
G=nx.read_gml('./football.gml')
# 社区发现
communities = list(community.label_propagation_communities(G))
print(communities)

图论工具igraph

可以处理百万级节点的网络
NetworkX比igraph好用
igraph比NetworkX强大

import igraph
g = igraph.Graph.Read_GML('./football.gml')
igraph.plot(g)
print(g.community_label_propagation())

最短路径问题Dijkstra& floyd

已知各城市之间距离，寻找从指定城市A到城市D的最短出行方案，或者各城市距离一致，给出需要最少中转方案

Dijkstra算法
floyd算法

Dijkstra算法原理

指定起点s,引进两个集合S和U。
S:是记录已求出最短路径的顶点(以及相应的最短路径长度)
U:记录还未求出最短路径的顶点(以及该顶点到起点s的距离)。
Step1，S中只有起点s，从U中找出路径最短的顶点，将其加入到S中
Step2，更新U中的顶点和顶点对应的路径
重复Step1和Step2 直到遍历完所有顶点
重复Step1，即更新S：从U中找出路径最短的顶点，加入到S中；
重复Step2，即更新U中的顶点和顶点对应的路径

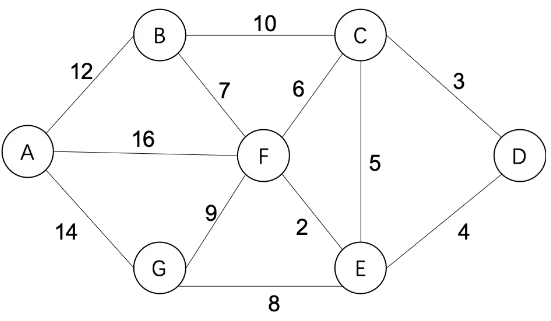
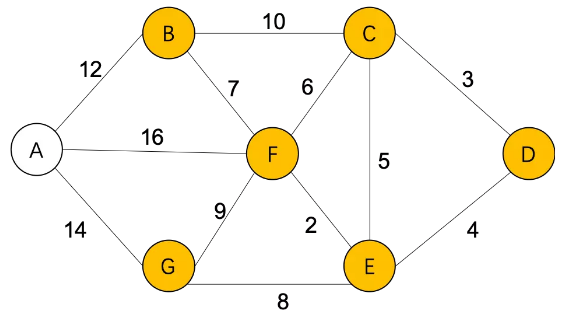
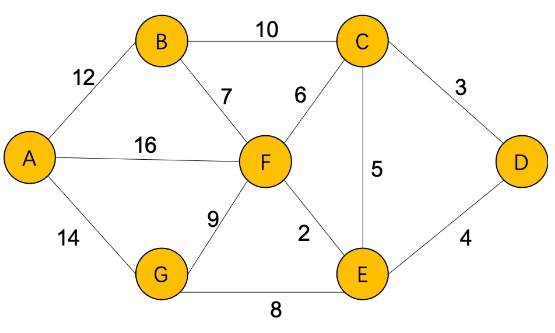
比如我们想要计算从D到其他城市的最短距离

Step1，S={D(0)}, U={A(∞),B(∞),C(3),E(4),F(∞),G(∞)}

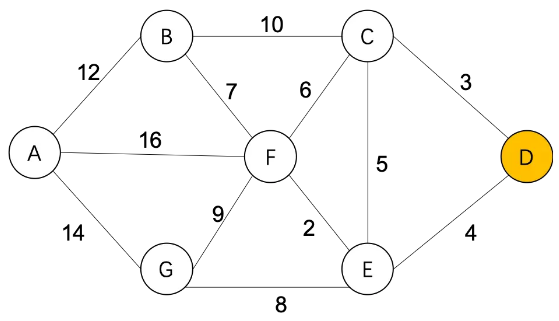
通过C，更新从D到其他城市的最短距离：

Step2，S={D(0),C(3)},

B(∞)=C(3)+10=13

F(∞)=C(3)+6=9

E(4)=C(3)+5=8（不更新）

U={A(∞),B(13),E(4),F(9),G(∞)}

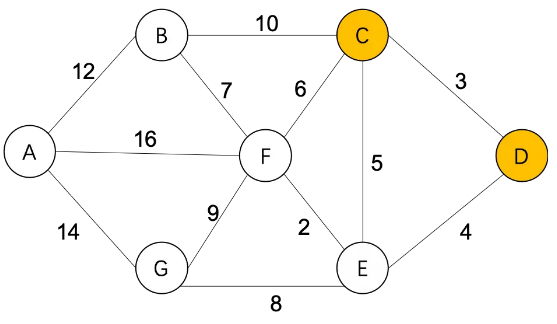
通过E，更新从D到其他城市的最短距离：

Step3，S={D(0),C(3),E(4)},

F(9)=E(4)+2=6

G(∞)=E(4)+8=12

U={A(∞),B(13),F(6),G(12)}

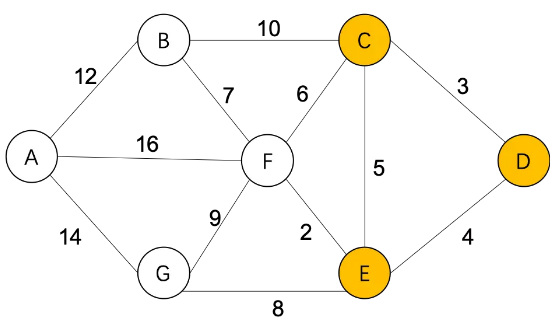
通过F，更新从D到其他城市的最短距离：

Step4，S={D(0),C(3),E(4),F(6)},

B(13)=F(6)+7=13 （不更新）

G(12)=F(6)+9=15 （不更新）

A(∞)=F(6)+16=22

U={A(22),B(13),G(12)}

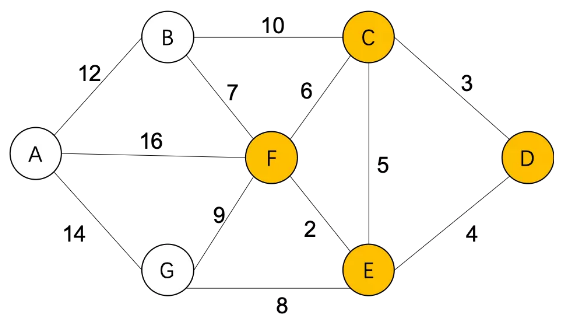
通过G，更新从D到其他城市的最短距离

Step5，S={D(0),C(3),E(4),F(6),G(12)},

A(22)=G(12)+14=26 （不更新）

U={A(22),B(13)}

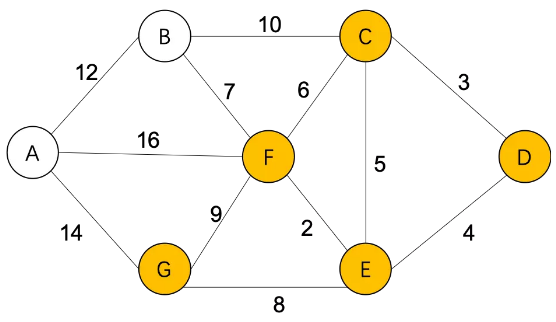
通过B，更新从D到其他城市的最短距离：

Step6，S={D(0),C(3),E(4),F(6),G(12),B(13)},

A(22)=B(13)+12=25 （不更新）

U={A(22)}

最终，得到从D到其他城市的最短距离：

S={D(0),C(3),E(4),F(6),G(12),B(13),A(22)}

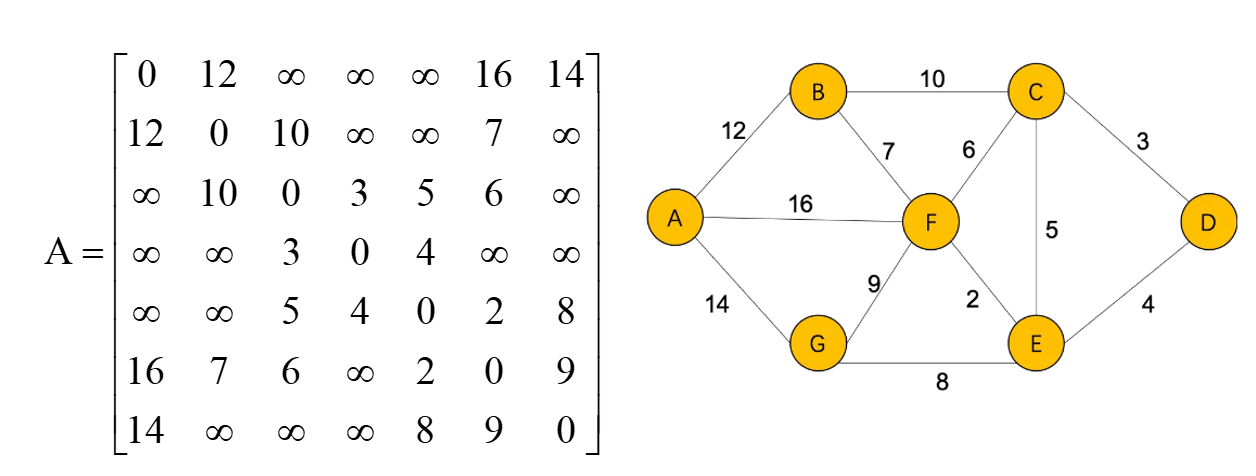
Floyd算法

初始的距离矩阵

Thinking：在图论算法中，为什么Floyd算法中k,i,j顺序不能颠倒，k不仅是它的顶点还代表是它的阶段 
n=7
for k in range(0, n):
    for i in range(0, n):
        for j in range(0, n):
            if a[i][k] + a[k][j] < a[i][j]:
                a[i][j] = a[i][k] + a[k][j]

print('各城市之间的最短距离：', a)
print('城市D到其他城市的最短距离：', a[3])

Floyd算法原理：

使用了动态规划的思想，将图中顶点编号为1-n
以两点之间最短距离经过的顶点中最大的顶点编号作为阶段，两点间目前算出的最短路径作为状态的值
假设为顶点编号i和j两点经过最大顶点编号不超过k的最短路径长度，那么：

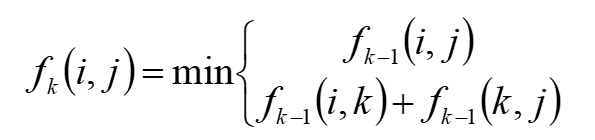
图论与推荐系统

推荐系统中的图论应用

PersonalRank，基于图的推荐算法
使用PageRank对节点进行影响力计算，由复杂网络=>Small World
按照影响力阈值进行筛选，对重要的节点网络进行可视化呈现

推荐系统中的图论应用

基于最短距离的好友推荐
社交网络已经变成了Small Word
原有的六度理论 => 3.57度（Facebook)
但好友之间存在关系远近，如何从指定用户A->C的找到最短路径

推荐系统中的图论应用

LPA，对用户群进行聚类=>用户画像
推荐系统初期，用户画像（标签）太少，未标签的用户太多
当标签数<<未标签数时，传统的监督式学习不work，可以采用半监督学习，即通过有限的标签传播至未标签的数据
图论是很有用的工具，不仅是推荐系统，很多应用场景都可以转化为图论问题

Thinking1：高德地图中的路径规划原理是怎样的？

Thinking2：football.gml 美国大学生足球联赛，包括115支球队，被分为12个联盟。为什么使用LPA标签传播进行社区发现，只发现了11个社区？

Thinking3：微博采用了类似FaceBook的EdgeRank算法，如果你给微博的信息流做设计，你会如何设计？

Action1：使用Python模拟下面的PageRank计算过程，求每个节点的影响力（迭代100次）

Action2：使用TextRank对新闻进行关键词提取，及文章摘要输出

　　新闻文本见：news_高考.txt https://new.qq.com/rain/a/20200724A0EFCU00

posted @ 2023-06-11 20:50 kris12 阅读(650) 评论(0) 收藏举报

刷新页面返回顶部

Arabic	Hebrew	Polish
Bulgarian	Hindi	Portuguese
Catalan	Hmong Daw	Romanian
Chinese Simplified	Hungarian	Russian
Chinese Traditional	Indonesian	Slovak
Czech	Italian	Slovenian
Danish	Japanese	Spanish
Dutch	Klingon	Swedish
English	Korean	Thai
Estonian	Latvian	Turkish
Finnish	Lithuanian	Ukrainian
French	Malay	Urdu
German	Maltese	Vietnamese
Greek	Norwegian	Welsh
Haitian Creole	Persian

kris12

Self-discipline gives me freedom.

PageRank| 图论与推荐系统

1. PageRank

什么是PageRank

PageRank简化模型

PageRank的随机浏览模型

PageRank的影响力和工具的使用

使用PageRank分析邮件中的人物关系及影响力

PageRank相关算法

2. 图论

图论工具的作用

什么是社区发现

社区发现常用算法LPA& COPRA

LPA算法

图论工具NetWorkX & igraph

最短路径问题Dijkstra& floyd

Dijkstra算法原理

Floyd算法

图论与推荐系统

公告

kris12

Self-discipline gives me freedom.

PageRank| 图论 与推荐系统

1. PageRank

什么是PageRank

PageRank简化模型

PageRank的随机浏览模型

PageRank的影响力和工具的使用

使用PageRank分析邮件中的人物关系及影响力

PageRank相关算法

2. 图论

图论工具的作用

什么是社区发现

社区发现常用算法LPA& COPRA

LPA算法

图论工具NetWorkX & igraph

最短路径问题Dijkstra& floyd

Dijkstra算法原理

Floyd算法

图论与推荐系统

公告

PageRank| 图论与推荐系统