十一. K-Means聚类算法
K-Means
最常用的机器学习聚类算法,且为典型的基于距离的聚类算法
K均值: 基于原型的、划分的距离技术,它试图发现用户指定个数(K)的簇
以欧式距离作为相似度测度
- 随机生成k个初始点作为质心;
- 将数据集中的数据按照距离质心的远近分到各个簇中;
- 将各个簇中的数据求平均值,作为新的质心,重复上一步,直到所有的簇不再改变;
注意点:
- 簇数量需要先给定,再进行聚类;
- 不适用于非线性边界;
- 数据量大,计算较慢;
无监督学习(输入进x,有对应的y),没有标注
聚类
- k均值
- 基于密度的聚类
- 最大期望聚类
降维
- 潜语义分析(LSA)
- 主成分分析(PCA)
- 奇异值分解(SVD)
k均值(k-means)是聚类算法中最为简单、高效的,属于无监督学习算法
核心思想:由用户指定k个初始质心(initial centroids),以作为聚类的类别(cluster),重复迭代直至算法收敛
基本算法流程:
选取k个初始质心(作为初始cluster);
repeat:
对每个样本点,计算得到距其最近的质心,将其类别标为该质心所对应的cluster;
重新计算k个cluser对应的质心;
until 质心不再发生变化或迭代达到上限
1. 聚类介绍
K-means 是一种在给定分组个数后,能够对数据进行自动归类,即聚类的算法。计算过程请看图中这个例子。
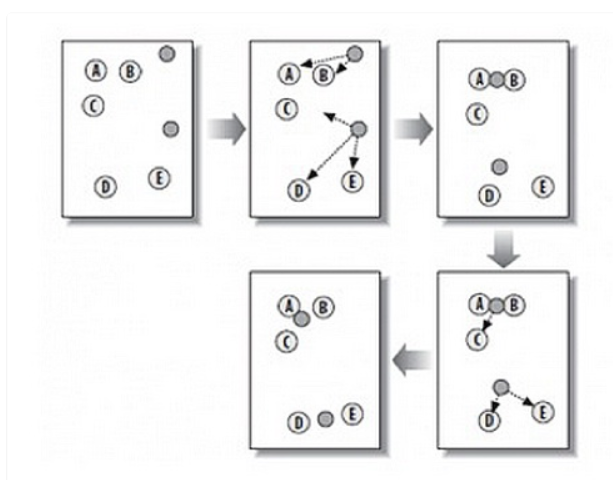
第 1 步:随机在图中取 K 个种子点,图中 K=2,即图中的实心小圆点。
第 2 步:求图中所有点到这 K 个种子点的距离,假如一个点离种子点 X 最近,那么这个点属于 X 点群。在图中,可以看到 A、B 属于上方的种子点,C、D、E 属于中部的种子点。
第 3 步:对已经分好组的两组数据,分别求其中心点。对于图中二维平面上的数据,求中心点最简单暴力的算法就是对当前同一个分组中所有点的 X 坐标和 Y 坐标分别求平均值,得到的 <x,y>就是中心
点。
第 4 步:重复第 2 步和第 3 步,直到每个分组的中心点不再移动。这时候,距每个中心点最近的点数据聚类为同一组数据。
K-means 算法原理简单,在知道分组个数的情况下,效果非常好,是聚类经典算法。通过聚类分析我们可以发现事物的内在规律:具有相似购买习惯的用户群体被聚类为一组,一方面可以直接针对不同
分组用户进行差别营销,线下渠道的话还可以根据分组情况进行市场划分;另一方面可以进一步分析,比如同组用户的其他统计特征还有哪些,并发现一些有价值的模式。
聚类的概念
无监督学习。它跟之前讲过的模型有着很不一样的特点: 输入样本是没有标签的。当使用逻辑回归模型时,我们手里是有输入的特征和输出标签的(比如广告属性作为特征,是否被点击作为最终的标签)。
假如没有标签或者数据没有被标记怎么办?难道就没有办法把这些数据用起来了吗?
显然不是,即便没有标签,我们仍然可以做很多方面的工作如聚类分析,这也是本章所要讨论的话题。举个例子,给定很多客户,而且我们知道每个客户的信息,这时候我们可以根据给定的客户信息把
这些客户做聚类,让那些拥有类似特性的客户能够聚在一起,比如分为有钱的客户、学生群体等。那这样的好处是什么呢?设想一个营销场景:东西是有贵有便宜的,那当然我们不希望把奢侈品推销给学生
群体,而是做基于用户分群的更为精准化的营销。这就是聚类的价值!
通过聚类我们可以把不同的事物分为几大类,但这时候并不要求一定有标签信息,因为聚类本身是基于事物的特性来分的。在聚类分析中,一个非常流行的万能算法叫作K-Means,中文叫K均值算法。
K-Means是一种最常用的聚类算法,也是一种无监督算法;
K-Means算法是最经典的聚类算法,几乎所有的聚类分析场景,你都可以使用K-Means,而且在营销场景上,它就是"King",所以不管从事数据分析师甚至是AI工程师,不知道K-Means是”不可原谅“的一
件事情。在面试中,面试官也经常问关于K-Means的问题。虽然算法简单,但也有一些需要深入理解的点。
聚类的应用场景
除了用户分群场景之外,K-Means也可以用来做图像的分割。那什么叫图像的分割呢? 实际上就是把一个图片按照某一个标准分成几个模块如背景、人像、信号灯、道路、建筑等等。那具体如何去分割
呢?这个问题也可以看作是聚类问题,我们期望的结果是:同一个模块内的像素点比较类似。虽然这是一个大概的思路,但也需要配合其他的操作(如平滑)才能把图片分割得更精准。

K-Means的迭代过程
在进入K-Means算法的细节之前,我们先了解一下它整个的计算过程,理解起来很简单。整个过程是迭代式的算法,每次迭代过程包含如下两步操作:
- 根据给定的中心点,计算出每一个样本的所属的类别(cluster),这个过程结束之后每一个样本都会有自己所属的类别。
- 之后把每一个类别所属的所有样本提取出来,计算平均值并作为新的中心点。
上述过程会不断循环,直到算法停止为止。上面的算法描述可能会觉得抽象;
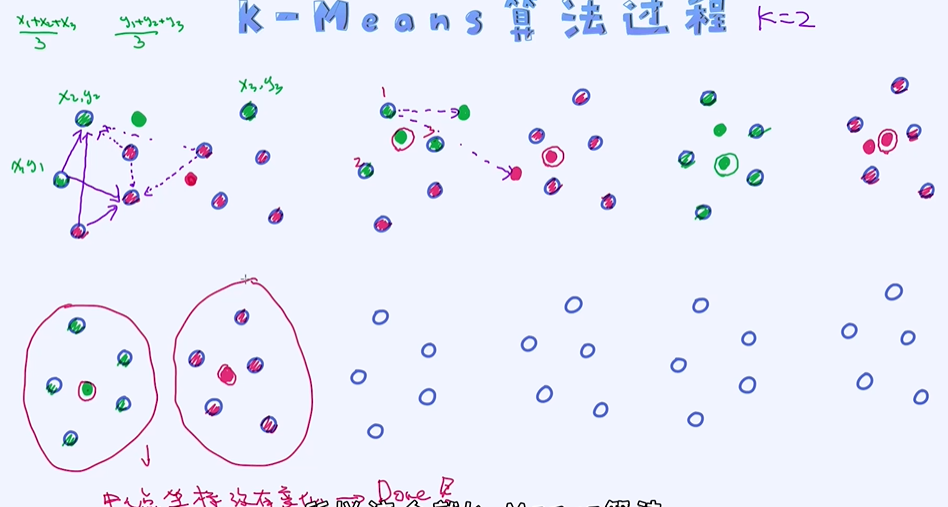
随机选取一个点作为中心点(一个红色的一个绿色的),然后分类(离哪个近就归属为哪个类别);
计算样本的平均值更新中心点的位置,如绿色的中心点 (x1+x2+x3)/ 3,(y1+y2+y3)/3; 依次循环
直到新的中心点和原来的中心点重合停止循环(中心坐标没有变化);
K-Means算法 - 循环迭代式的算法
① 初始化:
- 随机选择K 个点,作为初始中心点,每个点代表一个group;
② 交替更新:
- 计算每个点到所有中心点的距离,把最近的距离记录下来并把对应的group赋给当前的点;
- 针对于每一个group里的点,计算其平均并作为这个group的新的中心点。
从零实现一个K-Means算法。这部分的内容经常会在面试中问到,务必要掌握如何编写K-Means哦~
# 导入相应的包
from copy import deepcopy
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
# K-means里的K值
k = 3
# 随机初始化K个中心点,把结果存储在C
X = np.random.random((200, 2))*10
C_x = np.random.randint(0, np.max(X), size=k)
C_y = np.random.randint(0, np.max(X), size=k)
C = np.array(list(zip(C_x, C_y)), dtype=np.float32)
print("初始化之后的中心点:")
print(C)
# 把中心点也展示一下
plt.scatter(X[:,0], X[:,1], c='#050505', s=7)
plt.scatter(C[:,0], C[:,1], marker='*', s=300, c='g')
# 存储之前的中心点
C_old = np.zeros(C.shape)
clusters = np.zeros(len(X))
def dist(a, b, ax=1):
return np.linalg.norm(a - b, axis=ax)
error = dist(C, C_old, None)
# 循环算法,直到收敛。收敛的条件就是,判断当前的中心点与之前的中心点之间有没有变化,没有变化距离就会变成0,然后抛出异常
while error != 0:
# Assigning each value to its closest cluster
for i in range(len(X)):
distances = dist(X[i], C)
cluster = np.argmin(distances)
clusters[i] = cluster
# 在计算新的中心点之前,先把旧的中心点存下来,以便计算距离
C_old = deepcopy(C)
# 计算新的中心点
for i in range(k):
points = [X[j] for j in range(len(X)) if clusters[j] == i]
C[i] = np.mean(points, axis=0)
error = dist(C, C_old, None)
colors = ['r', 'g', 'b', 'y', 'c', 'm']
fig, ax = plt.subplots()
for i in range(k):
points = np.array([X[j] for j in range(len(X)) if clusters[j] == i])
ax.scatter(points[:, 0], points[:, 1], s=7, c=colors[i])
ax.scatter(C[:, 0], C[:, 1], marker='*', s=200, c='#050505')
------->
初始化之后的中心点:
[[8. 8.]
[6. 5.]
[6. 8.]]
<matplotlib.collections.PathCollection at 0x7ff904dbd350>
2. K-Means的细节
K-Means的目标函数
K-Means算法的核心流程如上,也就是迭代式过程。这个迭代式过程是如何得来的? 同时,我们根本没有讨论过K-Means的目标函数,是不是因为K-Means本身没有目标函数呢?实际上不是的!
K-Means的几个问题:
- 1. K-Means的目标函数是什么?
- 2. 一定会收敛吗?
- 3. 不同的初始化结果,会不会带来不一样的结果?
- 4. K如何选择?
① K-Means的目标函数
给定样本D={x1, x2, x3, x4...xn }和中心点u1,u2; 循环所有的样本,再循环所有的中心点(k=2),计算xi与ui之间的距离,L2的平方;
下面的目标函数不对的,因为这样计算会把样本属于两个中心点各计算一遍; 每一个样本点只能属于一个中心点;
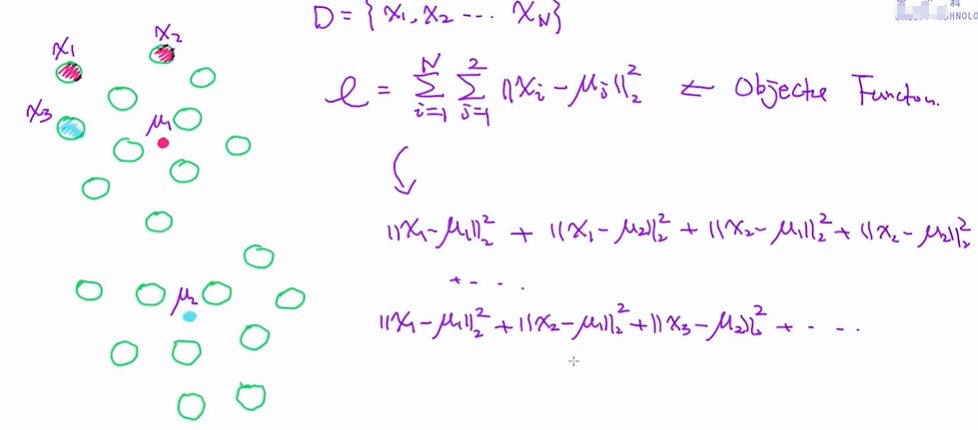
正确的目标函数
rik 0 or 1,xi属于第k个cluster的时候记作1,否则为0;

K-Means的目标函数里有两组不同的参数(中心点, 每个点所属的cluster), 相互耦合在一起, 如何去求解它们的最优解呢?
② 收敛
k-Means的实现,分两步骤循环迭代的过程,其实那个过程正好对应现在讲的优化方案:
- 固定中心点,求出每一个样本所属的最佳中心点的过程为算法里的第一步;
- 固定每个样本的类别,重新计算中心点的过程为算法里的第二步。是不是很神奇。
rik为n*k矩阵,uk为k个不同的向量;
交替试优化,①中心点已知的情况下,把每个点所属的颜色找到,等同于标记了它到底属于哪个中心点;(优化算法,目标函数会下降)
② 知道了样本跟哪个中心点近,求uk; 同一类样本的中心点即它的平均值作为新的中心点;第二步得到一个新的中心点 (目标函数会下降变小)
循环①②,最终会收敛即中心点的位置不会再变化;
这样子的一个优化算法其实跟EM算法很类似的,EM算法本质也属于coordinate Descent;
为了更好的理解EM算法可以看下GMM即高斯混合模型,K-means算法是高斯混合模型一个特定的版本;K-means一般叫做hard clustering,GMM一般叫做soft clustering;

③ 不同初始化结果,会不会带来不一样结果
K-Means的不同的初始化,会带来不同的结果。一开始生成的点不要改变。也就是针对于同一个样本,试着改变一下初始化的值,你会看到不同的结果。
不同初始化对参数的影响
那这个说明什么问题呢? 问题的本质在于我们每次得到的不是全局最优解,而是局部最优解! 类似的现象也会发生在神经网络当中,不同的初始化结果会带来不一样的结果。所以当我们使用神经网络的时
候会通过一些技巧去更好地初始化参数的。因为,对于这类的模型,好的初始化值会带来更好的最终结果的,也相当于得到了更好的局部最优解。那为什么k-means只能得到局部最优解呢? 其核心是非凸
函数。 如果一个目标函数是非凸函数,那我们其实不能保证或者没有办法得到全局最优解的! 如果想深入理解这些理论,建议学习一下凸优化理论,所有的细节都会在凸优化领域涉及到的。
④ K值如何选择
回顾一下KNN, 在KNN算法里我们也有一个参数叫K,但那个时候我们是通过交叉验证的方式来获得的。但在K-Means上能否使用交叉验证呢?答案是不可以的。因为我们数据根本就没有标签,我们是无
法评估的。 那怎么办呢?
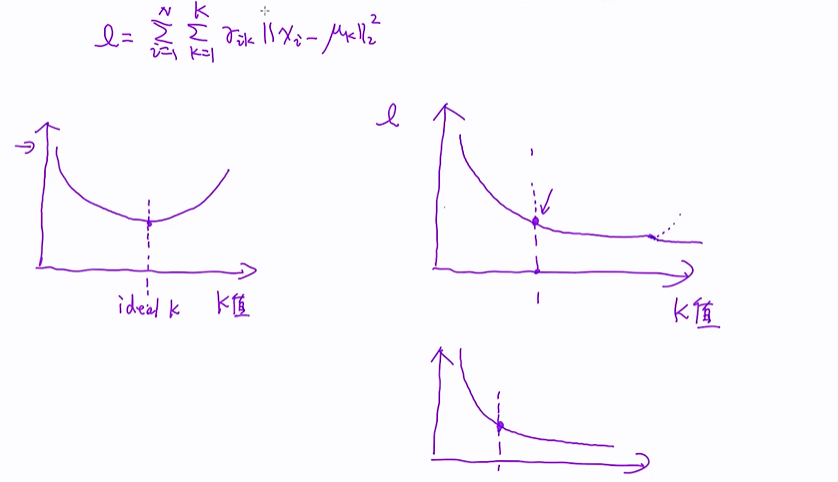
当k值逐渐变大的时候loss function 会逐渐变小的;在交叉验证中loss function会随着k值的增加先变小后变大,在监督学习中可以评估一个学习率,学习率的从大变小再变大,这个时候k值就很容易选择;
但在无监督学习中,没有特别好的一个评估方法,只能去看k值的变化如何影响loss function,k值变大损失函数变小,它并没有这样子一个拐点,一开始下降很快,到这个点之后下降会变慢;
那么这个点就是我们要选择的k值;
基于K-Means的矢量量化
矢量量化(Vector Quantization)的思路以及基于K-Means的实现。
K-Means的一个有趣的应用,叫作矢量量化(Vector Quantization),也经常用来做图像的压缩。
例如:假如一个图片大小为16*16, 而且用RGB来表示每一个像素点, 那对于这个图片, 我们需要存储多少个int型数值?
在RGB色彩空间里, 我们使用3个值来代表一个颜色, 所以总共有$16*16*3$。
具体怎么压缩图片? 道理很简单: 把类似的颜色统一替换成一个颜色! 假如我们用10种颜色来表示16*16的图片,那其实就节省了很多空间。
如下Vector Quantization的代码,学习一下如何结合k-means算法
# 导入相应的库
from pylab import imread,imshow,figure,show,subplot
from numpy import reshape,uint8,flipud
from sklearn.cluster import KMeans
from copy import deepcopy
# 读入图片数据
img = imread('/home/anaconda/data/Z_NLP/sample.jpg') # img: 图片的数据
# 把三维矩阵转换成二维的矩阵
pixel = reshape(img,(img.shape[0]*img.shape[1],3))
pixel_new = deepcopy(pixel)
print (img.shape)
# 创建k-means模型, 可以试着改一下 n_clusters参数试试
model = KMeans(n_clusters=3)
labels = model.fit_predict(pixel)
palette = model.cluster_centers_
for i in range(len(pixel)):
pixel_new[i,:] = palette[labels[i]]
# 展示重新构造的图片(压缩后的图片)
imshow(reshape(pixel_new, (img.shape[0], img.shape[1],3)))
------->
(315, 474, 3)
<matplotlib.image.AxesImage at 0x7fc68e08db10>
3. 从K-Means到层次聚类
层次聚类及常见的层次聚类方法
如何使用K-Means算法来做聚类。总体来讲,算法通过迭代的方式最后找出聚类的结果。另外一种聚类方法叫作层次聚类,通过层次聚类我们可以对原有样本数据做层次上的划分。相
反,K-Means算法本身是扁平化的,不具备任何层次的概念,而且使用K-Means的是需要提前指定K值的, 但很多时候我们并不能提前知道到底有分成多少个clusters。
层次聚类,另一方面,不需要提前指定K,而是在学习过程中动态地去选定一个合适的K值。
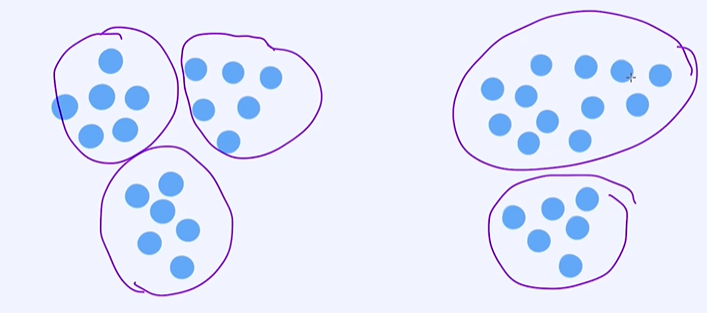
kmeans算法的缺点,下图中的第二个就无法更优的区分出样本属于哪个类别;
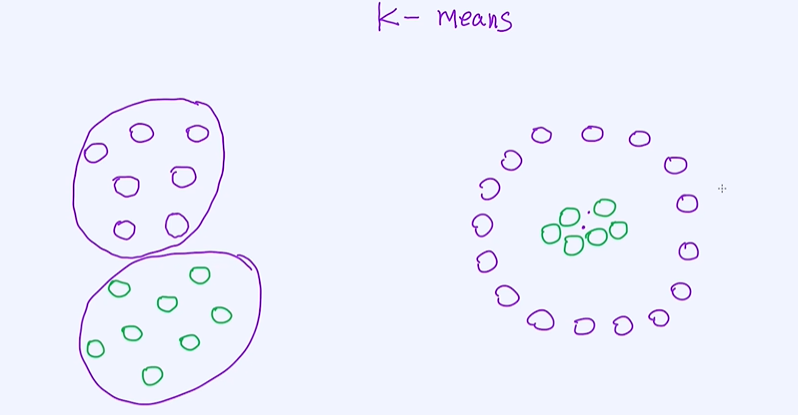
对于不规则的样本,K-Means算法的表现也会比较差。接下来,我们说一下层次关系。如上所述, K-Means算法在聚类时是不能捕获层次关系的。但层次关系有些时候还是挺有用的,比如通过观察人和
人之间的关系来挖掘哪些是事件的发起者、组织是如何运作的。层次聚类算法的好处就是通过算法自动给数据做分层,数据之间的层次关系一目了然,当然这也取决于数据和算法的准确性了。通过层次
聚类算法最终我们得到的是一个叫作Dendrogram的图,就是最后的结果。
DenDrogram
7个独立的点 cluster,把这些点一步步的合并起来,合并的过程涉及一些距离的计算,方式有:通过最短距离、最长距离、平均距离;
自底向上构造一个Single Large Cluster,y值代表这两个cluster的距离;
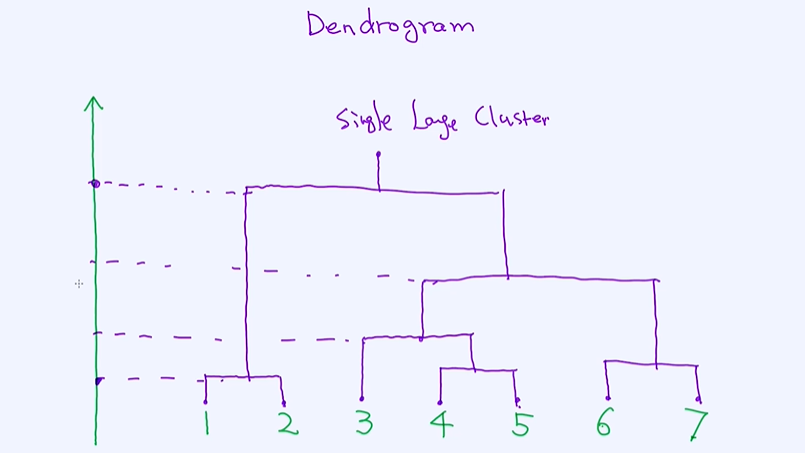
在层次聚类有两种方法论,一种是自下而上(最常见的),另外一种是自上而下(慢慢拆解成每个cluster);
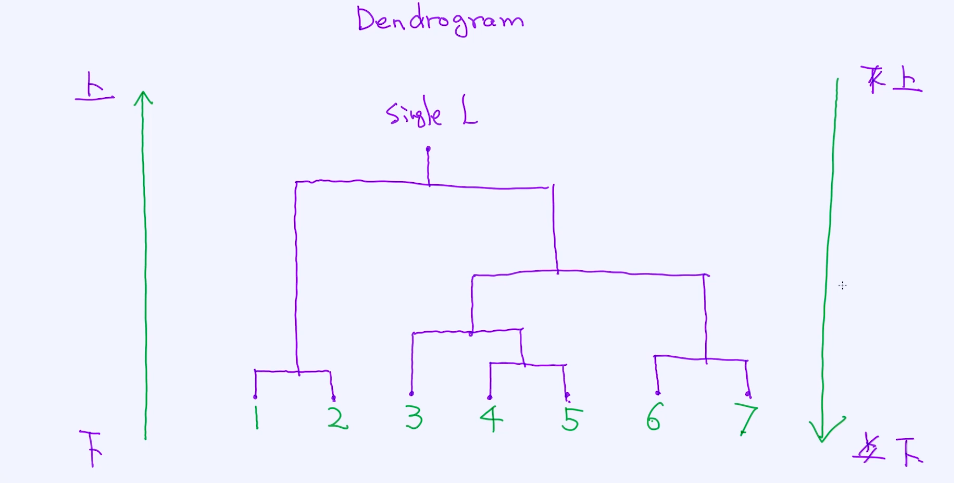
从下到上的层次聚类
如何使用自下而上的方式来做层次聚类,这是两种层次聚类算法中最为常见的一种。它的核心思想是: 一开始每一个点是一个cluster, 然后把类似的cluster慢慢做合并,到了最后就只剩一个
cluster了,这个时候即可以停下来。等做完所有步骤之后,我们就可以从现有的结果中选择合理的聚类结果了。比如我们设定一个阈值,然后基于这个阈值就可以得到相应的clusters了。自下而上层次聚
类过程的一个核心是: 相似度的计算,因为涉及到了不同cluster之间的合并。介绍三种常见的距离计算的方法: min、max、average
两个cluster之间最短、最长的距离、每个点之间的距离的平均值;
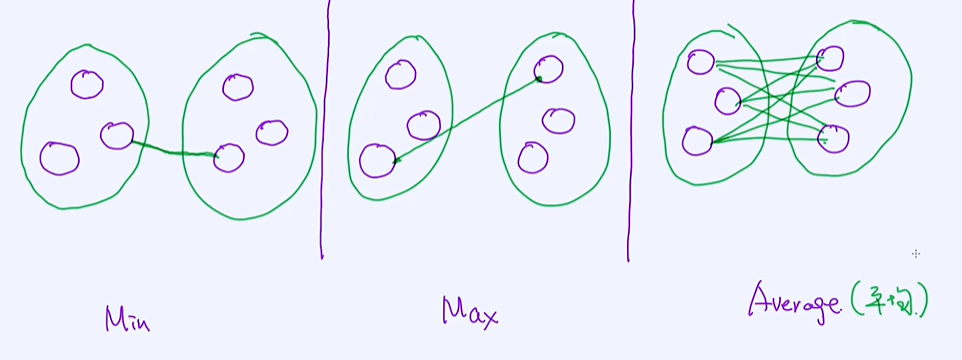
第一种情况是两个cluster的合并是基于最短距离来完成的,第二种情况是根据最长的距离,最后一种情况是通过平均距离来做合并的。下面分别来看下这三种不同的情况:
第一种 Min - Distance
每个样本一维的向量,如果两个样本之间的距离是一样的,比如②和③、④和⑤他们之间的距离都是1;
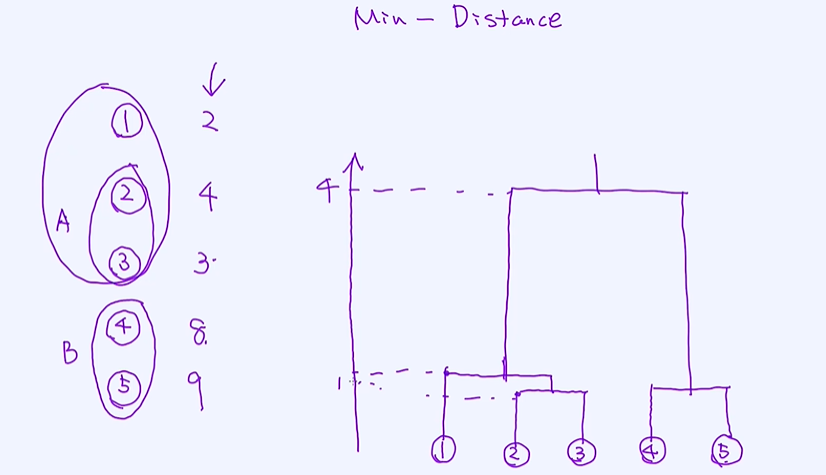
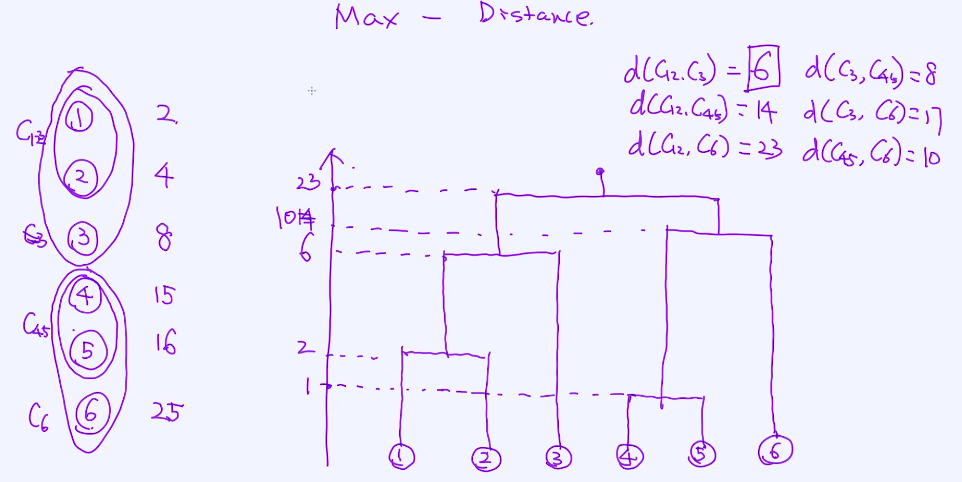
第二种:Max - Distance
在计算两个cluster之间距离时选择用max-distance去计算,选择合并的时候仍然使用的是最短的距离合并的;
所有的组合都要计算一遍,④和⑤之间的距离是最短的,合并一下;之后去计算剩下5个cluster两两之间的max-distance;最短的为①和②;
第三种:Average - Distance
平均距离的层次聚类 ,是三者中最稳的一种方法,也是最常用的;
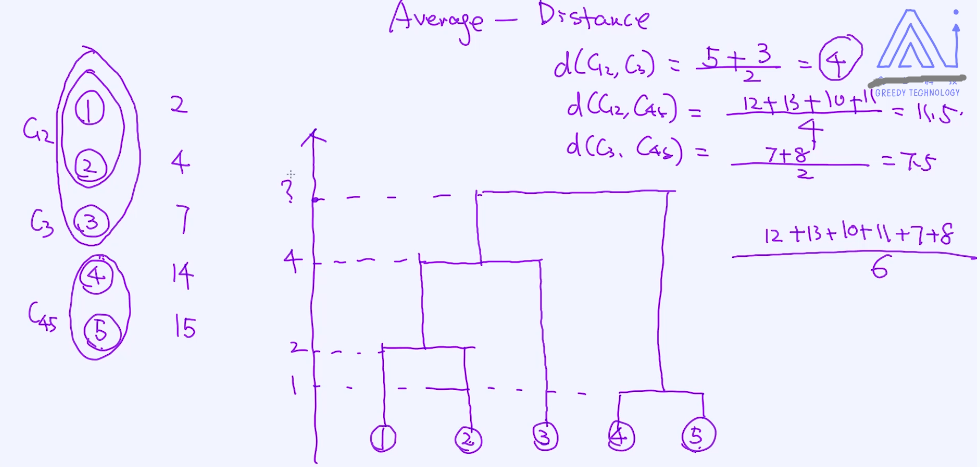
从上到下的层次聚类
另外一种层次聚类算法: 自上而下的方法。这个方法恰恰跟自下而上的方法相反。一开始我们只有一个大的cluster, 由所有的样本组成,之后逐步把每一个cluster切分成更小的,直到每一个cluster只包含
一个样本为止,这也意味着整个流程已完成。这个过程跟从下到上的方法恰恰相反,每次需要考虑的是如何把一个大的cluster切分成两个clusters,所以这里的切分标准格外重要。但相比自下而上的方
法,自上而下的聚类算法用的并不是那么多,大致了解一下就可以了。
在这里,介绍一个比较经典的自上而下的方法。 这个方案基于大家所熟悉的图算法,叫作最小生成树(minimum spanning tree)。
图论,MST的核心思想是在这些图中寻找一个路径一个树使得这个路径它会经过所有的点,通过路径把所有的点给串起来,串起来的同时所有的边的权重是最小的、所有边之和是最小化的;
严格意义来讲是寻找一颗树,把所有节点串起来,寻找的是让这些边的值之和最小化的那样的一棵树;下图中8个边串起来所有的点,同时保值所有边之和是最小化的 加起来为38=5+3+3+7+5+8+3+4
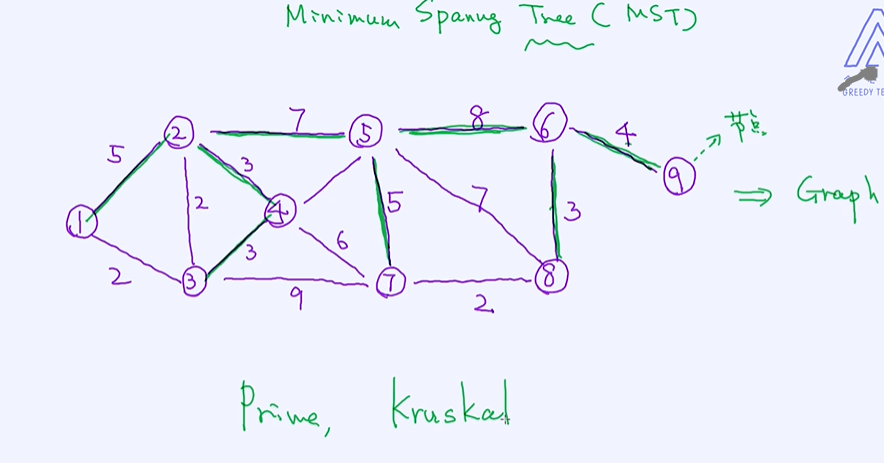
对于最小生成树,有几个比较常见的算法,分别是Prime和Kruskal算法。具体细节不在这里做详细阐述,感兴趣的朋友们可以自行去查看这两种算法。理解了MST之后,我们就可以开始谈论自上而下的
方法了。其实之后的操作非常简单:
计算两两之间的距离如图所示的一个graph,计算它的MST为1+4+7+1=13; 得到MST之后相当于是一个cluster,把其中最大的边7砍掉得到两个cluster;然后把4砍掉得到三个cluster;
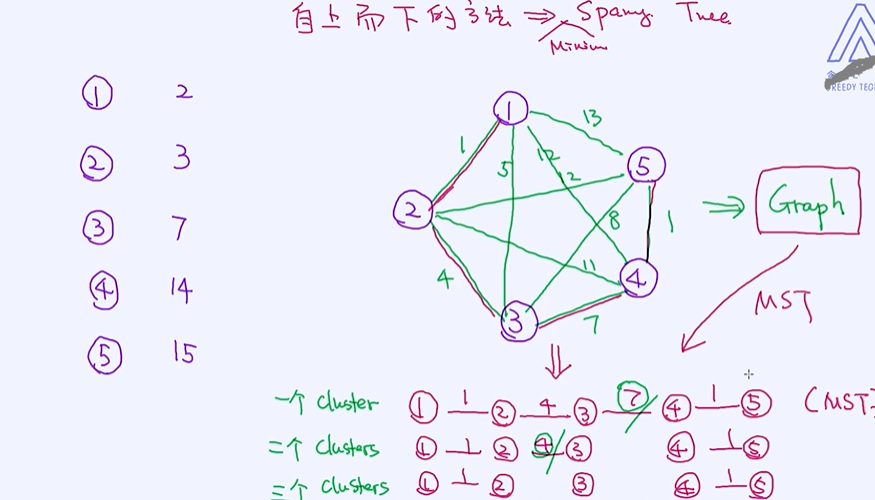
层次聚类算法只需要大家了解一下就可以了。在聚类领域,最常用的还是K-Means算法,其次就是讲过的自下而上的聚类方法了。
营销中的用户分层
1. 营销场景
设想一下,公司为了即将迎接双十一,要做一次针对于老用户的回馈活动,有几套商品要做促销。作为公司的营销负责人,需要设计出一套活动方案。
作为营销活动,一个核心问题是需要触达用户,并推销出产品。那对于哪些用户推销产品呢?
对于用户的选择一个最直接的方法是对于所有数据库中的客户群发消息, 并推送活动信息。
如果用户不具有潜在的购买需求,实际上是对客户的一种打扰,对这部分客户我们应该采取其他的激活措施。需要对用户分群, 按照用户的需求推送指定的计划。
如何对用户做分层呢? 比如给定一批用户,然后把他们分为A,B,C不同的群体,而且每个群体有自身的特点如有极强的购买能力和极强的购买可能性,较弱的购买意愿等等。实际上,这个问题的解决
思路有很多。其中一个简单的解决方法是基于一系列规则:
用于用户筛选的一些规则:
- A类用户:男性,单身,最近在平台上购买过商品,年收入10w以上;
- B类用户:男性,互联网从业人员,在平台上购买过商品;
- C类用户:女性,生活在一线城市,互联网从业人员;
上述方法显然是可行的。但问题点在于,随着属性(如男、是否单身等)的增多,用户群体个数也会增多,而且尝试的成本也会变高。同时,提出以上的规则本身需要一定的经验。那我们的问题是:除了这
种人为制定的基于规则的方法,有没有一套可用于营销场景的系统化的方法论? 这就是这个项目作业中,我们需要实现的内容。
2. RFM的一些细节
经典的营销模型-RFM
客户价值分析
在营销场景中,我们经常会遇到这样的一个问题:哪些用户的价值高? 我们如何根据客户价值给用户分群?对于这个问题,RFM就是一种答案。 那具体什么是RFM模型呢? 如何应用RFM做用户分群呢?
RFM里的每个字符代表什么意思呢?
RFM中的R
我们从客户价值的角度来分析这个问题。什么样的客户价值比较高? 举个例子,如果有两位客户A和B, A是前天光顾了一家火锅店,B在3个月前光顾了同一家火锅店,那从客户价值角度,A,B中哪一位
用户价值更高?
答案很显然是用户A,因为前天来到了此火锅店。如果他对味道和服务都满意,有可能在未来一段时间内重新光顾一次。但相反,用户B没有光顾此店已经有3个多月了,有可能这个用户搬家了,也有可能
这个用户觉得这家店并不是很好吃,失去了兴趣。
这就是所谓的R(recency),指的就是近期光顾的客户要比很早以前光顾的客户价值更高,也是符合常理的。
RFM中的F
接着再来看还有哪些因素可能会影响客户价值。除了最近有无光顾之外,还有一个重要标准是光顾了多少次,这就有点像“常客”的意思。假如用户A在过去一年光顾了这家火锅店10次,用户B只光顾了2
次,说明用户A对这家火锅店的忠诚度更高,也就是他的价值是更高的。
这就是所谓的F(frequency),说的是频次。一个人光顾的频次越高就说明越忠实,价值也就越高。
RFM中的M
最后,再来看另外一个维度。假如有两个客户A,B,A在过去一年在这个火锅店消费了一万多,B消费了五百,那谁的客户价值更高呢? 显然是A,因为他花了更多的钱,至少说明他的购买能力是要强于B
的。这就是所谓的M(moneytary),指的是一个人在过去一段时间消费了多少钱,消费越多就说明此人的价值就越高。
RFM模型
- R(Recency): 最近一次的购买是发生在什么时候?一个月前,还是半年前?
- F(Frequency):在过去一段时间内,购买了多少次 ?
- M(Moneytary):在过去 一段时间内,总共消费了多少钱?
了解了RFM中的每个维度含义之后,我们就可以根据这三个维度对人群做分层了;
把不同数据映射到不同bucket中:
①先排序;
②基于quantile的方式来分为4层(前25%分到第一个bucket 1中、依次,bucket数越大用户价值越大);
③ R越小用户价值越大;F越大用户价值越大;M越大用户价值越大;
④ 将segment的值相加即可得到score;(用户价值的分数)
A、B、C三类用户,阈值的选择是根据人工经验,也可以通过AB测试的方式选择更好的阈值;经典的基于RFM来分群;

在上面的分群方法里,我们先把每一值映射到了不同的bin, 然后根据自定义的规则对人群做了分群。这种方法的好处在于简单,而且可解释性比较强。但缺点是引入了很多人工的处理和规则。另外,如
果我们要考虑更多的维度,需要的规则就变得更复杂,这也给规则的设计增添了更大的难度,一种解决方案是使用K-Means算法。
3. 基于K-Means的用户分群以及评估方法
作为经典的聚类算法,K-Means也可以作为用户分群的一种方法。具体实施也很简单,直接在用户数据上跑一下K-Means模型就可以了,但提前要设定K值。这里需要注意的一点是要做必要的数据预处
理。因为K-Means算法依赖距离的计算,如果有些特征值很大,就会极大影响距离计算的结果。所以在使用K-Means算法的时候,提前把每个特征的值范围做一些归一化。
用户分群的效果评估
首先,聚类分析是无监督算法,所以做聚类分析之前是没有标签数据的。在没有标签数据的情况下,只能依靠从数据本身的理解或者靠经验来设定分群。但随着活动的正式进行,我们可以逐渐获得一些
反馈数据的。比如A类客户的转化率有多少,B类客户的转化率有多少等等。
根据用户的反馈数据,我们就可以调整分层策略了。但这个过程也需要一些技巧。需要思考的一点是:如何使用最小成本来尝试并调整分层策略?一般可采用的方法是A/B测试。假设我们手里有两种分层方
案A和B。A方案是目前来讲比较有效的而且稳定的,B方案是想要尝试的而且很可能更有效的。
我们可以针对一部分用户实施B方案,之后再看一下效果。如果发现效果要优于方案A,我们可以逐步在更多的人群里开始使用B方法。 其实任何的AI产品都离不开A/B测试,核心是如何用最小成本去验证
某个方案的优越性。
最后的问题是,如何去评估呢? 这个其实要看业务场景了! 比如营销里我们关注的是转化率,那指标就定转化率。如果关注的新增用户,那这就是我们的结果指标。所以具体的指标,需要看当前业务,没
有一个标准的答案。
在本项目中,我们基于用户购买数据(Transaction Data)做用户的细分,依次使用RFM模型和K-means算法。 通过本项目的练习,你即将会学到如何使用RFM和K-means来解决实际精准营销问题,以及
它们之间的区别。 基于这类方法论,我们可以把用户分为金牌用户、银牌用户,普通用户等类别



 浙公网安备 33010602011771号
浙公网安备 33010602011771号