六. 朴素贝叶斯
朴素贝叶斯模型
1. 理解朴素贝叶斯
贝叶斯公式是一种基于条件概率的分类算法,如果我们已经知道 A 和 B 的发生概率,并且知道了 B 发生情况下 A 发生的概率,可以用贝叶斯公式计算 A 发生的情况下 B 发生的概率。事实上,我们可以
根据 A 的情况,即输入数据,判断 B 的概率,即 B 的可能性,进而进行分类。举个例子:假设一所学校里男生占 60%,女生占 40%。男生总是穿长裤,女生则一半穿长裤一半穿裙子。假设你走在校园
中,迎面走来一个穿长裤的学生,你能够推断出这个穿长裤学生是男生的概率是多少吗?答案是 75%,具体算法是:

意思是 A 发生的条件下 B 发生的概率,等于 B 发生的条件下 A 发生的概率,乘以 B 发生的概率,除以 A 发生的概率。还是上面这个例子,如果我问你迎面走来穿裙子的学生是女生的概率是多少。同样
带入贝叶斯公式,可以计算出是女生的概率为 100%。其实这个结果我们根据常识也能推断出来,但是很多时候,常识受各种因素的干扰,会出现偏差。比如有人看到一篇博士生给初中学历老板打工的新
闻,就感叹读书无用。事实上,只是少见多怪,样本量太少而已。而大量数据的统计规律则能准确反映事物的分类概率。
贝叶斯分类的一个典型的应用场合是垃圾邮件分类,通过对样本邮件的统计,我们知道每个词在邮件中出现的概率 P(Ai),我们也知道正常邮件概率 P(B0) 和垃圾邮件的概率 P(B1),还可以统计出垃圾邮
件中各个词的出现概率 P(Ai∣B1),那么现在一封新邮件到来,我们就可以根据邮件中出现的词,计算 P(B1∣Ai),即得到这些词出现情况下,邮件为垃圾邮件的概率,进而判断邮件是否为垃圾邮件。
朴素贝叶斯的应用
朴素贝叶斯模型是文本领域永恒的经典,广泛应用在各类文本分析的任务上。只要遇到了文本分类问题,第一个需要想到的方法就是朴素贝叶斯,它在文本分类任务上是一个非常靠谱的基准(baseline)。
比如对于垃圾邮件的分类,朴素贝叶斯是一个极其有效且简单的模型。
不要小看一个简单的模型。实际上,我们真正需要的是既简单同时又有效的模型,因为最终的目的是用最小成本来解决问题。一个简单的模型既有利于短时间内训练,也有助于后续的维护和管理。
朴素贝叶斯,这个名字里的“朴素”源自于概率统计里的“条件独立”,因为在构造模型过程中做了一层基于条件独立的简化操作。 朴素贝叶斯模型作为分类算法,非常适合用在各类文本分类任务上,如:
- 垃圾邮件分类: 自动判断一个邮件是否为垃圾邮件或者正常邮件;
- 文本主题分类: 把一个文本按照主题做分类如体育类、娱乐类;
- 情感分析: 把给定的文本分类成正面或者负面情感;
朴素贝叶斯核心思想
垃圾邮件示例:
您提交的#3152号工单:来自李先生的留言 有更新。
请点击以下链接查看工单处理进度:
https://tingyun.kf5.com/hc/request/view/3152/
要添加另外的工单评论,请回复此邮件
启发: 有些单词经常出现在垃圾邮件里;
朴素贝叶斯的核心思想极其简单: 其实就是统计出不同文本类别中出现的单词的词频。
对于垃圾邮件的分类任务,我们需要统计出哪些单词经常出现在垃圾邮件,哪些单词经常出现在正常邮件就可以了。
如果在邮件里看到了“广告”,“购买”,“链接”等关键词,可以认为这个很可能是垃圾邮件,因为这些单词经常出现在垃圾邮件中,其实很多邮件过滤系统是这样过滤垃圾邮件的。当然,我们也可以自行设
定一些规则来过滤垃圾邮件。在这种规则里,我们通常也是指定哪些单词跟垃圾邮件相关。
对于垃圾邮件的分类, 直接弄一份关键词词库, 然后一旦邮件里包含了这些词就认为是垃圾邮件,
如果按照词库来判断一个邮件是垃圾邮件还是正常邮件,这有点类似于通常说的“一刀切”的方法。其实更好的方案是加入一些概率的要素,把不确定性也加进来,比如虽然出现了“广告”,“推销”等关键词,但同时
也出现了大量的没有包含在词库里的单词,最终按照概率的角度可以判定为是正常邮件,这实际上就是朴素贝叶斯模型的核心思想。
如果以词库为依据来直接判定邮件的种类是存在一定的问题的。它的问题在于,即便出现了一些广告类单词,但并不一定是垃圾邮件; 没有出现任何广告类单词也不一定是正常邮件。所以每个单词虽然有倾向性,但不能以偏概全。
如何把这些不同的单词以概率统计的方式整合在一起呢? 答案就是朴素贝叶斯!
利用朴素贝叶斯识别垃圾邮件

使用朴素贝叶斯模型一般需要两步骤:
首先,统计出每一个单词对一个邮件成为垃圾邮件或正常邮件的贡献。比如 p ( 广告 | 垃圾 ) 、p( 广告∣正常 )分别代表在 垃圾 / 正常邮件里出现 “广告”这个关键词的概率。
其次,用这些统计的结果对一个新的邮件做预测
朴素贝叶斯广泛地应用在文本分类任务中,其中最为经典的场景为垃圾文本分类(如垃圾邮件分类: 给定一个邮件,把它自动分类为垃圾或者正常邮件)。这个任务本身是属于文本分析任务,因为对应的数
据均为文本类型,所以对于此类任务我们首先需要把文本转换成向量的形式,然后再带入到模型当中。
import pandas as pd
import numpy as np
import matplotlib.mlab as mlab
import matplotlib.pyplot as plt
# 读取spam.csv文件
df = pd.read_csv("/home/anaconda/data/Z_NLP/spam.csv", encoding='latin')
df.head()
# 重命名数据中的v1和v2列,使得拥有更好的可读性
df.rename(columns={'v1':'Label', 'v2':'Text'}, inplace=True)
df.head()
# 把'ham'和'spam'标签重新命名为数字0和1
df['numLabel'] = df['Label'].map({'ham':0, 'spam':1})
df.head()
# 统计有多少个ham,有多少个spam
print ("# of ham : ", len(df[df.numLabel == 0]), " # of spam: ", len(df[df.numLabel == 1]))
print ("# of total samples: ", len(df))
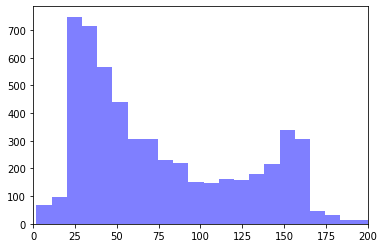
# 统计文本的长度信息,并画出一个histogram
text_lengths = [len(df.loc[i,'Text']) for i in range(len(df))]
plt.hist(text_lengths, 100, facecolor='blue', alpha=0.5)
plt.xlim([0,200])
plt.show()
# 导入英文的停用词库
from sklearn.feature_extraction.text import CountVectorizer
# 构建文本的向量 (基于词频的表示)
vectorizer = CountVectorizer()
X = vectorizer.fit_transform(df.Text)
y = df.numLabel
# 把数据分成训练数据和测试数据
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, random_state=100)
print ("训练数据中的样本个数: ", X_train.shape[0], "测试数据中的样本个数: ", X_test.shape[0])
# 利用朴素贝叶斯做训练
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import accuracy_score
clf = MultinomialNB(alpha=1.0, fit_prior=True)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
print("accuracy on test data: ", accuracy_score(y_test, y_pred))
# 打印混淆矩阵
from sklearn.metrics import confusion_matrix
confusion_matrix(y_test, y_pred, labels=[0, 1])
======>>>
# of ham : 4825 # of spam: 747
# of total samples: 5572
<Figure size 640x480 with 1 Axes>
训练数据中的样本个数: 4457 测试数据中的样本个数: 1115
accuracy on test data: 0.97847533632287
array([[956, 14],
[ 10, 135]])
2. 朴素贝叶斯模型的训练
朴素贝叶斯的训练过程,也是词频统计的过程。
计算单词的概率
正如之前说过的一样,朴素贝叶斯训练的核心步骤就是统计各个单词在不同类别中的概率。 举个例子,当我们去分析一个文件是否为垃圾邮件或者正常邮件时,一个判断的依据是如果很多跟垃圾邮件相关的关键
词出现在了文本里,我们即可以把它归类为垃圾邮件,这些决策最终基于概率统计的方式来实现。
总体来讲,朴素贝叶斯分为两个阶段:
- 计算每个单词在不同分类中所出现的概率,这个概率是基于语料库(训练数据)来获得的。
- 利用已经计算好的概率,再结合贝叶斯定理就可以算出对于一个新的文本,它属于某一个类别的概率值,并通过这个结果做最后的分类决策。
单词"购买"的概率;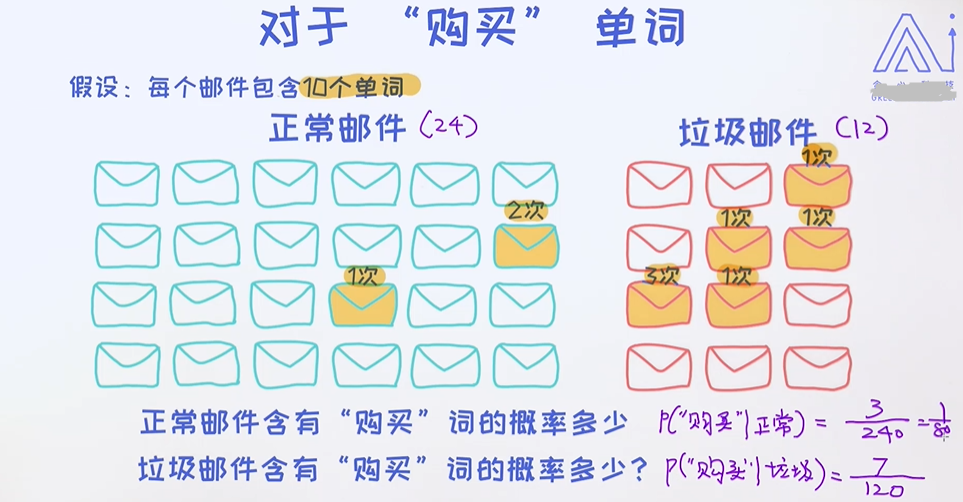
单词"物品"的概率;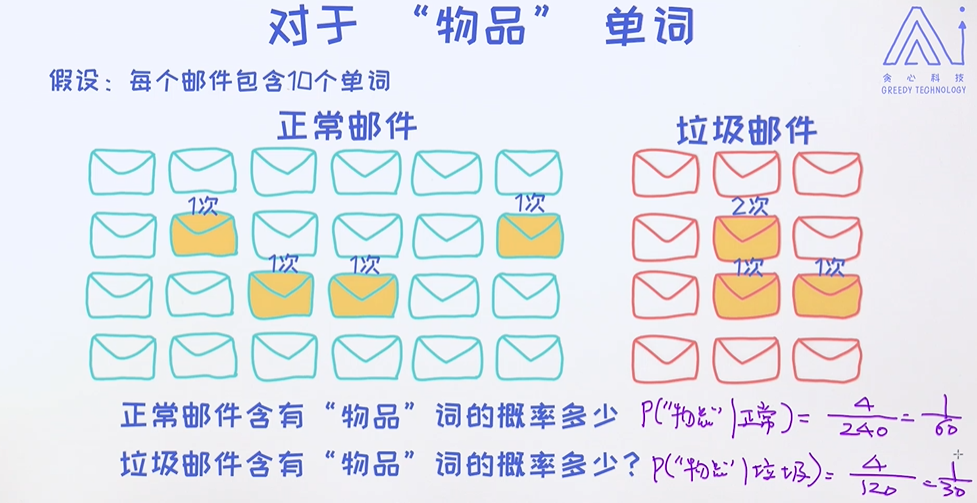
单词"不是"的概率;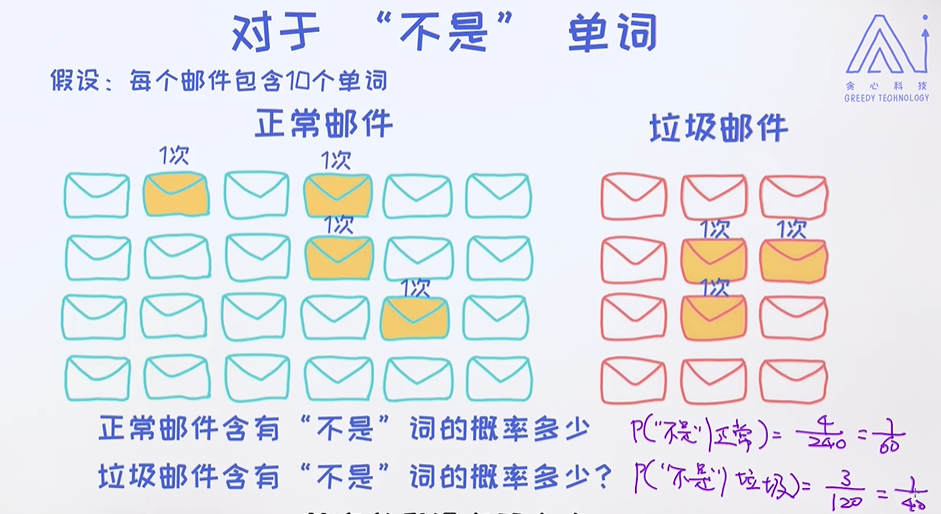
单词"广告"的概率;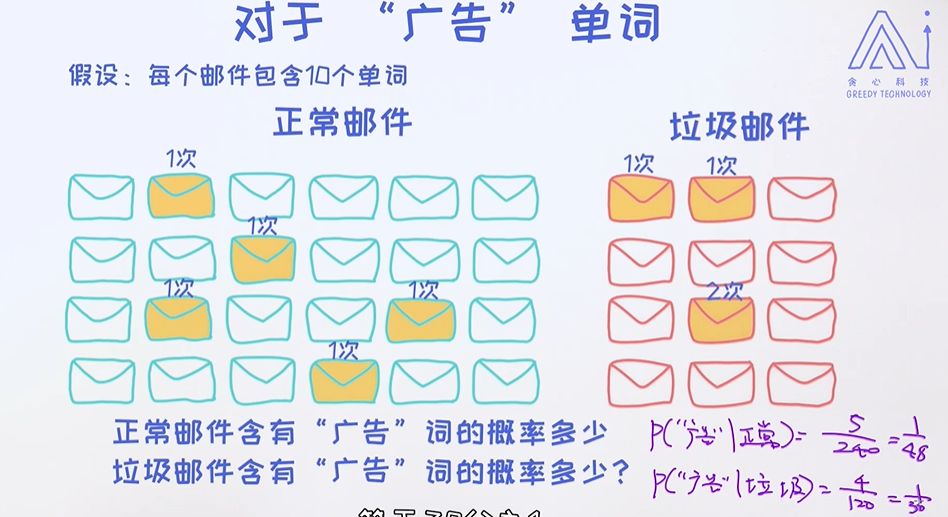
单词"这"的 概率;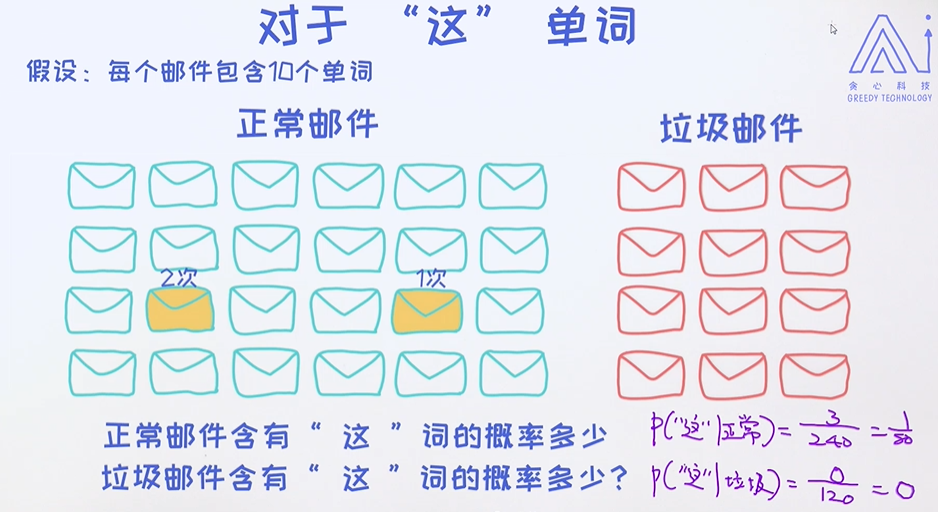
正常邮件和垃圾邮件的占比概率;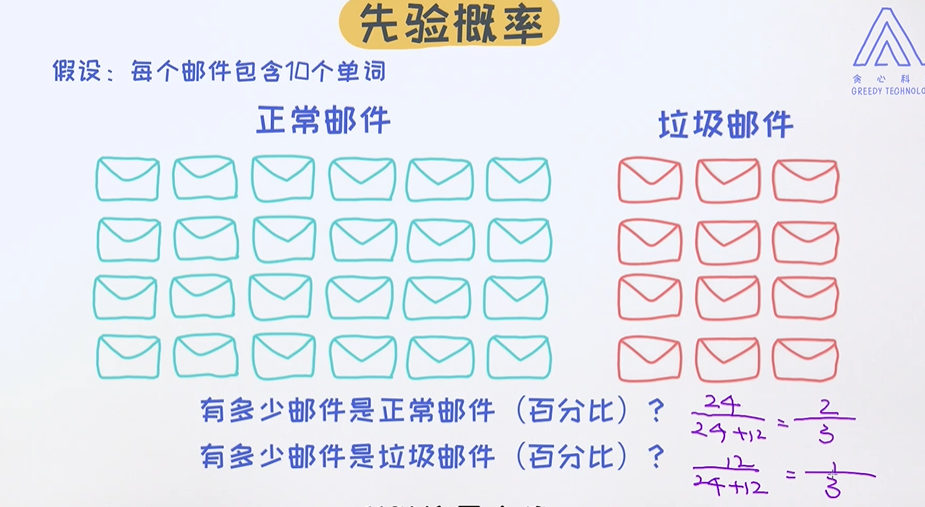
利用计算好的概率来预测
目前为止我们已经算好了每一个单词在不同类别中的概率,以及垃圾邮件和正常邮件在整个数据中的占比,后者也称之为先验概率(prior)。统计完这些概率之后,如何使用它们来预测一个邮件是否为垃圾
或者正常邮件呢?

Bayes_Theorem
为了表示两个条件概率值 p(垃圾|邮件内容)和 p(正常|邮件内容),需要用到一个著名的概率公式-贝叶斯定理。利用贝叶斯定理可以把上述条件概率做进一步的分解,最终可以计算出它们的值
把两个随机变量x,y做了替换,两个变量的联合概率;
计算预测概率
在预测过程中我们使用一个叫作条件独立(conditional independence)的假设。简单来讲,基于这个性质可以把条件概率p(x,y|z)p(x,y∣z)写成p(x,y|z)=p(x|z)p(y|z)p(x,y∣z)=p(x∣z)p(y∣z)的形式,
这时候可以说变量 x和变量 y是条件独立于变量zz的。
这也是为什么把朴素贝叶斯说成“朴素”的主要原因,因为做了一层计算上的简化。如果不使用条件独立的假设,我们是不能把概率p(x,y|z)p(x,y∣z)写成上述形式的,这样一来问题就变得格外地复杂。
条件独立的性质可以延展到更多的变量,如p(x_1,x_2,x_3|y)=p(x_1|y)p(x_2|y)p(x_3|y)p(x1,x2,x3∣y)=p(x1∣y)p(x2∣y)p(x3∣y)。当我们把这里的每个变量x_ixi看作是每一个单词的时候,就得到了朴
素贝叶斯模型。
朴素贝叶斯模型的训练其实就是统计和计算每个单词在不同条件下的概率;
P(这| 广告) = 0 导致整个P(垃圾| 邮件内容) 为0是不合理的,且其他指标的概率都大于 P(正常) ,导致这封邮件成了正常邮件;

处理为零的情况-平滑操作
另外,在上述过程中可以看到分子的计算过程涉及到了很多概率的乘积,一旦遇到这种情形,就要知道可能会有潜在的风险。比如其中一个概率值等于0,那不管其他概率值是多少,最后的结果一定为
0,有点类似于“功亏一篑“的情况,明明出现了很多垃圾邮件相关的单词,就是因为其中的一个概率0,最后判定为属于垃圾邮件的概率为0,这显然是不合理的。为了处理这种情况,有一个关键性操作叫
作平滑(smoothing),其中最为常见的平滑方法为加一平滑(add-one smoothing)。

下面例子,通过给出的垃圾邮件、正常邮件来预测新邮件是否是垃圾邮件
词库 n = 9个单词,使用平滑操作add-one smoothing,分子加1,分母加词库n大小
需要比较P(垃圾| S) 和P(正常| S) 的大小,故P(S) 不用求解,
当我们计算每个0-1之间概率乘积时,把很小的值乘很多次的时候很容易出现underflow,添加log;

3. 从最大似然角度来理解朴素贝叶斯
从最大似然估计的角度来理解朴素贝叶斯模型。换句话说,首先根据最大似然估计来构造朴素贝叶斯的目标函数,接下来再通过优化手段来求解朴素贝叶斯的最优解。
朴素贝叶斯模型以及如何估算每个单词的概率,并用这个概率来预测一个文本的分类。
但有没有思考过: 为什么要计算这些单词的概率? 它的依据是什么? 这个问题看似有点愚蠢,但实际上需要认真地思考才能发现其背后的奥妙之处。
计算语料库中每个单词的条件概率,这个过程实际上是模型训练的过程。另外,模型的训练过程其实就是寻找最优解的过程。
从另外一个更严谨的角度来学习朴素贝叶斯。首先,构造朴素贝叶斯的目标函数,之后再试着去寻找朴素贝叶斯的最优解。最终会发现,以这种方式得出来的最优解恰恰就是计算出的结果;
为了推导出朴素贝叶斯的目标函数,仍需要从最大似然开始入手,并通过最大似然估计来获得朴素贝叶斯的目标函数。

有五个样本D,

投硬币问题
4次正的、2次反的,很容易求出出现正面的概率为4/6 = 2/3;其实我们无意中使用的就是最大似然估计;
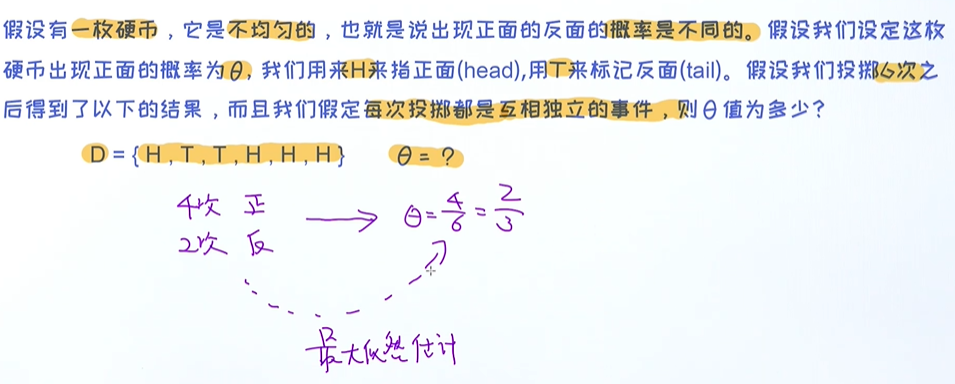
硬币问题的最大似然估计
最大化 f(θ) ,即优化问题, 求导;

构造朴素贝叶斯的最大似然估计
样本数据D x1特征向量,y1为标签(垃圾邮件or正常邮件)
x1分为两类
- 离散型变量(文本类)
- 连续型变量
逻辑回归中是P(Yi| Xi)的条件概率,朴素贝叶斯是最大化P(Xi, yi)的联合概率 ,这种叫生成式的最大似然估计,生成模型;而逻辑回归中条件概率叫 判别模型;
最大化每个样本的联合概率时(特征向量和标签);
P(Yi)为先验概率,P(Xi, Yi)在类别给定的情况下看到文档的概率 也叫似然概率;
1、2、3一共有三个文档,是否出现为0和1;V个词库,Wj 表示代表词库里的第j个单词;x1j表示向量x1中第j个单词,得到下面的最大似然,但是没有参数 需要引入参数值θ

θ矩阵,每一列代表1、2、3,在每个类别的情况下每个单词出现的概率是多大;类别有三列,行为词库的大小为|v|;
先验概率,类似一个向量,它的大小即类别的大小这里有三个,叫做Pi(π);
把参数θ、π代入最大似然估计, k为文档类别,nk有多少个文档属于类别k,θkj表示当前文档属于k类的情况下看到第j个单词的概率;

有了朴素贝叶斯的目标函数之后,剩下的环节无非就是寻找最优解的过程了。从上述目标函数中可以发现它具有一个限制条件。那这样的目标函数我们应该如何去优化呢?
这种优化问题也称之为带限制条件的优化(constrained optimization)。
带限制条件的优化
带限制条件的优化相比无限制条件的优化稍微复杂一些。对于无限制条件的优化问题,在逻辑回归中已经涉及到了。 回顾无限制条件的优化,同时重点来学习带限制条件的优化问题如何解决。

带约束条件的优化 - 拉格朗日乘法项
线与圆的交点; 通过拉格朗日乘法项把f(x) 做一个整改,f(x, y, λ) 把λ 加进来,把条件x2 + y2=0代入到f(x,y)中
分别对x,y,λ求导

朴素贝叶斯目标函数的优化
当理解了如何求解带限制条件的优化问题之后,就可以试着来求解朴素贝叶斯目标函数的最优解了。 整个过程有一些繁琐,但用到的基本知识都是上面提过的内容,只要细心去体会,应该都能看得懂。
利用拉格朗日乘法项改造目标函数,

最终的结果 θkj分子表示在所有属于第k类文档里出现了多少次的第j个单词,分母是属于第k个所有文档里总共出现了多少个单词;

通过这种方式得出来的结果恰好跟上节的结果是吻合的,所以从这个例子可以看出,任何一个计算结果实际上都是有背后的依据的。为了更好地理解每一个知识点,我们需要尝试着去深挖底层的细节,
这样才能达到打通知识体系的目的。
4. 生成模型与判别模型
两种模型直观上的区别
生成模型和判别模型在机器学习领域是一个非常重要的概念。任意的机器学习模型我们均可以归类为判别模型或者生成模型。那具体什么是生成模型,什么是判别模型呢?
从字面上来看, 生成模型模型可以生成数据;(生成模型的一大功能是,训练好之后可以用来生成新的数据。)
让机器学习写程序?让机器学习学习画画?让机器编一个曲子?这些事情生成模型都可以做,当然效果好不好是另一回事情了。
训练一个生成模型通常不仅可以用来完成识别或者分类任务,也可以用来生成一些新的数据,包括图片、文章、代码、视频、音频等等。 虽然生成这些数据本身具有很大挑战,但至少从理论的角度来讲
是一条可行的道路。
从字面上来理解, 判别模型主要用来判别样本的类别;(不同于生成模型,判别模型是没有办法用来生成新数据的。虽然生成即可以用来解决判别问题,也可以生成数据,但这不代表生成模型由于判别模型。
实际上,很多判别任务(如分类任务)上, 判别模型的表现要好于生成模型。)
判别模型的初衷是用来解决判别问题,而且只做一件事情(不像生成模型即可以解决分类问题也可以解决生成数据的问题),所以在分类问题上它的效果通常要优于生成模型的。接下来试着从另外一个角度
来理解它俩之间的区别。
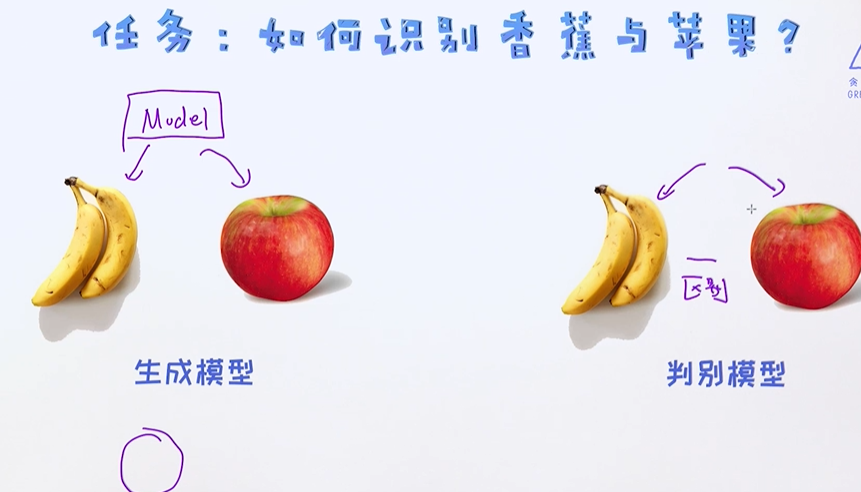
生成模型需要把每个类别物体的特征全部记录下来,接下来来了一个新物体,需要去跟之前记忆去做比较;
判别模型只需要知道它俩的区别即可,不需要知道它们的特征;
从数学角度去比较
生成模型为联合概率,判别模型通过条件概率去改造最大似然;
生成模型中包含了判别模型里的P(y|x),它既做了判别模型的事情也去记录每个类别它的一个特点,它做了两件事情,而判别模型只做了一个事即判别,从这个角度也可以看出为什么在大多数分类问题上
判别模型的效果要优于生成模型,判别模型只做一件事判别 它不会生成每个样本;

从数据的角度理解它俩的区别
生成模型即可做判别的任务又可以做生成的任务;如果只是做一个判别分类,那么判别模型的效果是优于生成模型的,但在数据量比较小的情况下生成模型的效果比判别模型要好;

逻辑回归的最大似然是基于条件概率来构造的,但朴素贝叶斯的最大似然是基于x和y的联合概率来构造的;所以逻辑回归是判别模型,朴素贝叶斯是生成模型;




 浙公网安备 33010602011771号
浙公网安备 33010602011771号