四. 模型的泛化
模型的泛化
1. 过拟合
在机器学习建模中面临一个极其重要的问题 - “过拟合”。
基于逻辑回归模型来剖析什么是过拟合,如何正确地理解过拟合现象,减轻过拟合现象的几种方法。
逻辑回归的参数
即便是一个简单的逻辑回归模型,当我们去调用模型时需要选择性地设置它的一些参数,这些参数的设定对模型训练后的结果一般会产生关键的作用。在建模中,对于这些参数的合理设定也称之为”调参
“过程。
当数据线性可分的时候对于逻辑回归模型,考虑一种特殊情况,也就是当数据线性可分的时候。比如在二维空间里,我们可以画出一条直线完美地区分开正负两类样本。
逻辑回归模型更偏向找第2条线,那么w就是无穷大的;为了证明这一点需要更最大似然和条件概率做一个联系,从目标函数的角度:
在逻辑回归中定义过一个条件概率,x给定的情况下要去预测y=0或y=1的概率;当w变得很大时,wTx+b也是无穷大,e-(wTx+b) 趋近于0;
整个逻辑回归的目标函数,逻辑回归的最大似然MLE ,通过一些优化算法最大化MLE 最大似然,
当yi=1的时候,我们希望P(yi=1|xi w,b)越大越好,即它趋近于1;
当yi=0的时候,1-yi = 1,后半部分会起作用;1-logP(yi=1|xi w,b) 越大越好,也就是 logP(yi=1|xi w,b) 越小越好,log是严格递增的,即P(yi=1|xi w,b) 越小越好,最小值为0;

如果给定的数据是线性可分的, 这时候使用逻辑回归模型学出来的参数变得很大。
控制参数的大小
那如何控制参数的大小呢? 也就是如何让参数变得小一些?
一种方式是人为地在目标函数上添加一个惩罚项(Penalty),用来惩罚过大的参数。由于引入了这样的一个项,在优化的过程中我们倾向于选择绝对值小的参数。
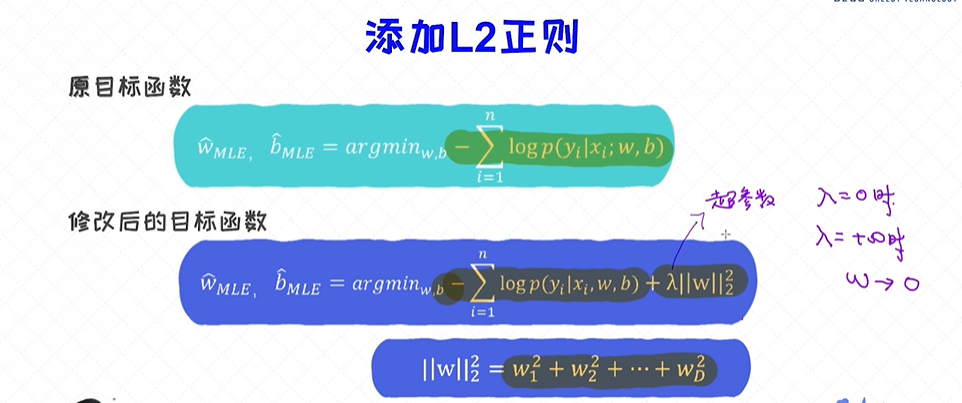
当参数的绝对值变大的时候,L2范数的值也会相应地变大,这就跟最小化目标函数是矛盾的。所以加入L2范数之后,优化过程倾向于选择绝对值小的参数。 那除了L2范数我们能否选择其他形式的惩罚项
呢?当然可以,但每一种惩罚项的作用是不太一样的。
原逻辑回归的目标函数,通过最小化这一项来得到参数w和b,这种训练的方法叫最大似然估计MLE(Maximum likelihood estimation) ,当样本线性可分的时候,w和b倾向于非常大,为了解决这个问题,在原来目标函数的基础之上加了λ乘以 w的L2正则即 λ||w||22 , 可以很好的控制w 的大小;
如果想要w的值越来越小,那么λ的值可以越来越大些,调节λ 的方法叫交叉验证 cross validation ;
加入L2正则之后,对原本的梯度下降法会产生什么样的变化和影响。
我们的目的是要去最小化这个式子,它有两部分组成,①是之前讨论的损失函数; ②新加入的正则项;
从下面推导可以得到,加入L2正则对梯度下降法没产生太大的影响,w只是多了 2λw,对时间复杂度没有产生本质的区别;

梯度下降不一定能够找到全局的最优解,有可能是一个局部最优解
如果损失函数是凸函数,梯度下降法得到的解就一定是全局最优解

λ的作用
λ是可控参数,需要人为地去调节。当λ值变小或者变大时,它所带来的影响是不一样的。这种参数也称之为超参数(hyperparameter),可以想象为是模型的开关,
通过调节此开关让模型的行为产生不一样的结果。
λ 对整个式子的影响,如果λ 比较大我们把更多精力放在调节 λ||w||22 这项上;如果λ 比较小更多精力放在前边;
当λ 变得很大的时候,因为我们要 λ||w||22 最小化,我们需要保证w趋近于0;
当λ = 0 的时候,正则这一项就起不到作用了;
这是两个极端;
λ 的取值范围一般为 0.1 或者 0.001 或者1 等

什么是过拟合
当没有加任何惩罚项的情况下参数变得非常大。那这种现象又如何理解呢?
实际上,一个模型存在过拟合现象的时候,它的参数趋向于变大。

模型参数变大是导致过拟合的一个重要原因, 如何去理解这句话呢? 举个简单的例子, 假设一个模型最后学出来的参数值为(0.3, 0.5, 89997)(0.3,0.5,89997),是一个三维的向量。
由于第三个参数值过大,导致模型的不稳定性。即便对应于第三个参数的输入值变化很小(如0.01),但由于参数系数过大,就会导致对输出的影响也会很大,最终让模型变得不稳定。 因为在真实的环境中,输入
信号不可避免地会包含一些噪声。
2. 防止过拟合
模型的泛化能力(generalization),过拟合(overfitting)以及正则(regularization)。
在模型的训练过程中,解决过拟合是至关重要的步骤,所谓的调参实际上是来解决模型过拟合问题。
模型的泛化能力
在建模中,我们的目标是构建出泛化(generalization)能力很强的模型。对泛化通俗的理解是,模型可以很好地适应新的环境,这就类似于一个有能力的人,到什么岗位上都可以做出出色的成绩;一个优秀
的学生具备很强的举一反三的能力;
把上述理念套在模型上,我们可以说成: 一个好的模型不仅在训练数据上表现好,而且在测试或者线上真实环境上表现也比较稳定且出色,这就是对泛化的一个通俗的理解。
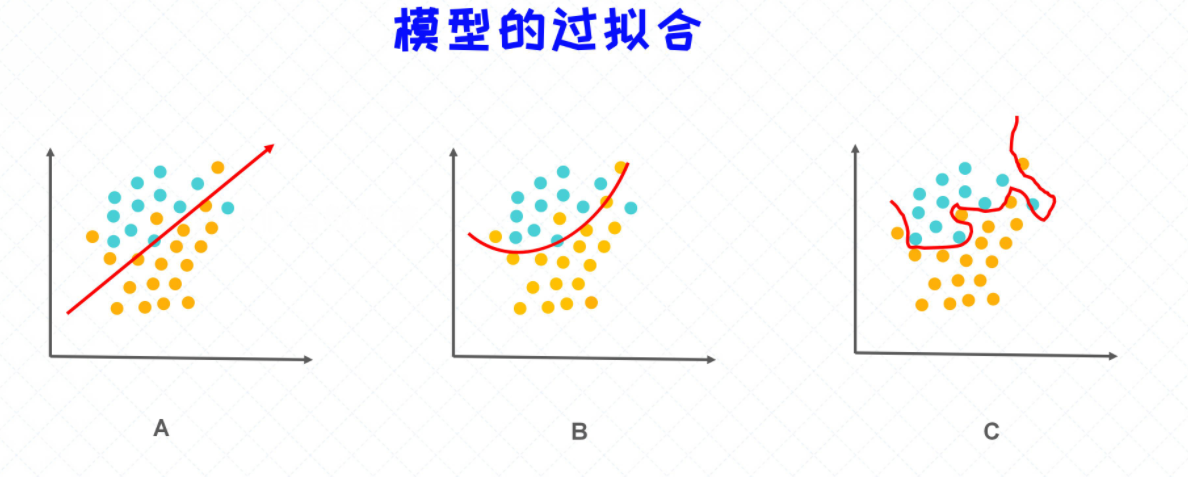
以上三幅图中(二分类问题),我们分别画出了三个不同的决策边界(decision boundary), 所谓的决策边界, 在这里代表的是用来划分两种类别的分界线。
模型复杂度与过拟合
对于过拟合来讲,有一种规律: 越复杂的模型越容易过拟合。
比如SVM相比逻辑回归更容易过拟合; 深度神经网络相比浅层神经网络更容易过拟合; 所以,对于复杂一些的模型,我们需要设计出好的机制来避免过拟合。
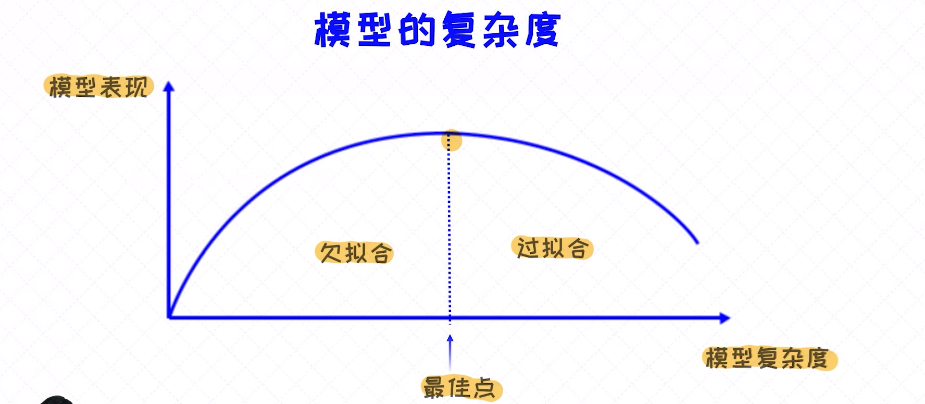
欠拟合是在训练数据集上没有训练好,就会导致一个欠拟合的现象;通过调参找个一个最佳的点;绝大多数情况下是关注一个过拟合;
如何避免过拟合?
- 数据量的增加;
- 使用更简单的模型;
- 加入正则项;
正则的作用
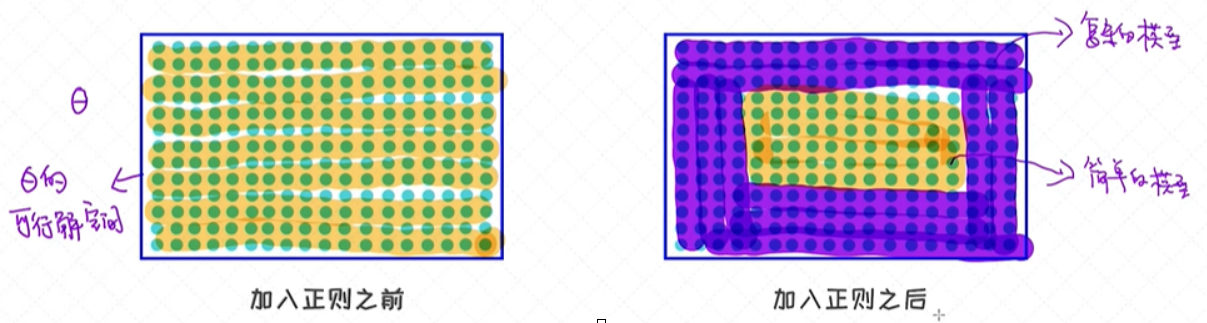
在一个模型里加入正则,会让训练出来的模型变得更”简单“,这句话应需要从正则的本质说起。
正则的作用:对可行解空间 (feasible region)的限制
加入正则做了一层筛选的工作,先筛选出简单模型对应的θ,然后从这个空间里面再去寻找最好的模型出来;从空间角度,正则是帮我们自动筛选了简单的空间,
从简单的空间中再去选出合适的θ值;
正则的种类
正则的应用非常广泛,它既可以用在逻辑回归也可以用在线性回归、支持向量机、神经网络、以及各类深度学习模型当中。正则的种类也繁多,常见的有L1和L2正则,当然还有L0等正则也被很多人使用,但每一个正则之间还是有很大的区别。
3. L1和L2的正则
L1和L2正则作为模型过拟合的一种解决手段,在建模阶段的应用非常广泛。 另外,对于每一个正则项,我们需要调节其参数,这个过程称之为交叉验证。
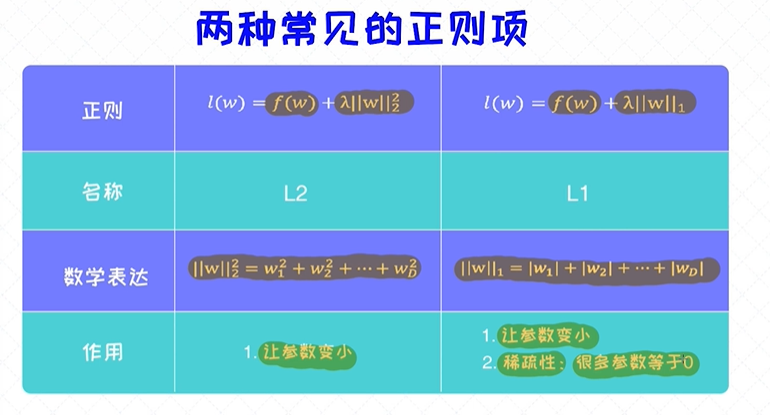
两种常见的正则
在模型训练阶段,为了防止模型的过拟合,我们通常会加入正则来提升模型的泛化能力。其中L1和L2正则的使用最为广泛。这些正则项会促使模型的参数变小,从而让学出来的模型本身变简单,起到防
止过拟合的效果。
L1和L2正则的特点
总体来讲,L1正则和L2正则都可以用来防止模型的过拟合,但L1相比L2正则,还具有另外一种特性,就是让模型的参数变稀疏。
首先,试着理解一下什么叫稀疏。通俗来讲,假如模型有100个参数,通过 L1正则的引入最终学出来的参数里可能 90个以上都是0,这叫作稀疏性。
相反,如果使用L2正则则没有这样的特点。那为什么L1正则会让模型的参数变稀疏,但L2正则就没有这类特点呢?
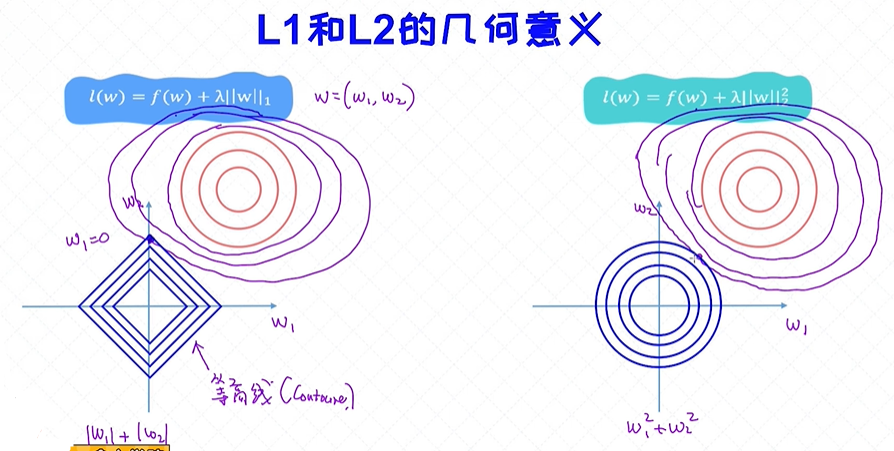
如下图:w为二维的向量,左福图是L1的正则:|w1|+|w2| ,等高线上的值都是一样的;
右幅图是L2正则, (w1)2 + (w2)2
f(w)的等高线如右上图,我们需要去找f(w) 和L1、L2正则的最小值,即几幅图的交集,
左福图L1正则和f(w)的交集在顶点上,w1=0;
右幅图L2正则和f(w)的交集是非零解;这就可以理解L1正则为啥会有稀疏性的原因了;
# 随机生成样本数据。 二分类问题,每一个类别生成5000个样本数据 import numpy as np np.random.seed(12) num_observations = 100 # 生成正负样本各100个 # 利用高斯分布来生成样本,首先需要生成covariance matrix # 由于假设我们生成20维的特征向量,所以矩阵大小为20*20 rand_m = np.random.rand(20,20) # 保证矩阵为PSD矩阵(半正定) cov = np.matmul(rand_m.T, rand_m) # 通过高斯分布生成样本 x1 = np.random.multivariate_normal(np.random.rand(20), cov, num_observations) x2 = np.random.multivariate_normal(np.random.rand(20)+5, cov, num_observations) X = np.vstack((x1, x2)).astype(np.float32) y = np.hstack((np.zeros(num_observations), np.ones(num_observations))) from sklearn.linear_model import LogisticRegression # 使用L1的正则,C为控制正则的参数。C值越大,正则项的强度会越弱。 clf = LogisticRegression(fit_intercept=True, C=0.1, penalty='l1') clf.fit(X, y) print ("(L1)逻辑回归的参数w为: ", clf.coef_) # 使用L2的正则,C为控制正则的参数。C值越大,正则项的强度就会越弱 clf = LogisticRegression(fit_intercept=True, C=0.1, penalty='l2') clf.fit(X, y) print ("(L2)逻辑回归的参数w为: ", clf.coef_) ====>> (L1)逻辑回归的参数w为: [[
0. 0. 0.00424842 0. 0.07096305 -0.29531785 0. -0.3403994 0. 0.78414305 0. 0.10093459 0. 0. 0. -0.04089472 0. 0. 0.41568396 0. ]] (L2)逻辑回归的参数w为: [[
-0.06020774 -0.08587293 0.06269959 0.0218838 0.36622515 -0.45899841 0.11456309 -0.44218794 -0.24780618 0.87767764 -0.32403048 0.27800343 0.34313572 0.16393398 -0.14322159 -0.22759078 0.09331433 -0.22950935 0.48553032 0.1213868 ]]
特征选择
由于使用L1正则之后,很多参数变成了0,这自然就起到了特征选择的目的。比如模型有100个参数,每一个参数对应于一个特征,
最后训练完之后只有10个参数不为0,则自然就帮我们选出了有效的特征。
L1的不足之处
L1既有稀疏性(选出特征)的特点,也有防止过拟合的特点,那是否意味着相比L2正则更好用呢? 其实不然,这个问题还要看L1正则具体的细节。可以从两个方面来讨论L1正则所存在的潜在的问题:
- 1. 计算上的挑战
- 2. 特征选择上的挑战。
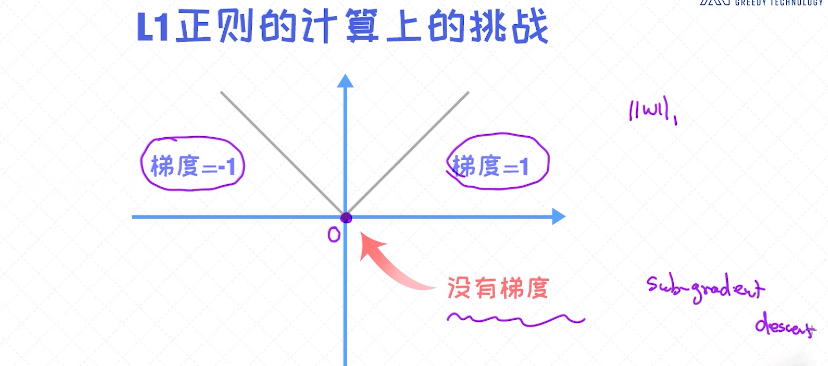
当w为正时,它的梯度为1,w为负时,它的梯度为-1; 当w=0时它是没有梯度的。导致L1正则不容易融合到梯度下降法的计算中,要考虑一个零点;
对L1正则我们使用的算法像subgradient descent ;

L1正则从几个相关性相似的特征中随机 筛选一个特征如f1、f7、f6,因为是随机性,并不是最好的那一个;解决方案是:
把L1 + L2正则拼到一块,相应的复杂度也变高了;
L1和L2的使用场景
总结起来,面对模型训练中的过拟合问题,L2是最为常用的正则。至于L1正则,它的首要应用场景在我们希望参数变稀疏的时候。
交叉验证

调参其实就是调节的这个C 值;
交叉验证是机器学习建模中非常重要的一步,也是大多数人所说的”调参“的过程。 回到逻辑回归的例子,我们为了避免过拟合,在模型目标函数上加入了L2正则,但这时候正则项前面多出了一个参数叫
作 λ, 那如何去设置这个参数呢? 什么样的参数对模型的训练是最有利的 ?
调参中很重要的一个概念,K折交叉验证
λ =[0.01, 0.1, 1] 等一次次去尝试;
假设k=5,把所有的数据都分为五等分,每一次把其中一个等分设为一个验证集,每一次的验证集是不一样的;
- 当λ=0.01时候的准确率 acc10.01 ,
- 重新训练一个模型准确率 acc20.01
- ......
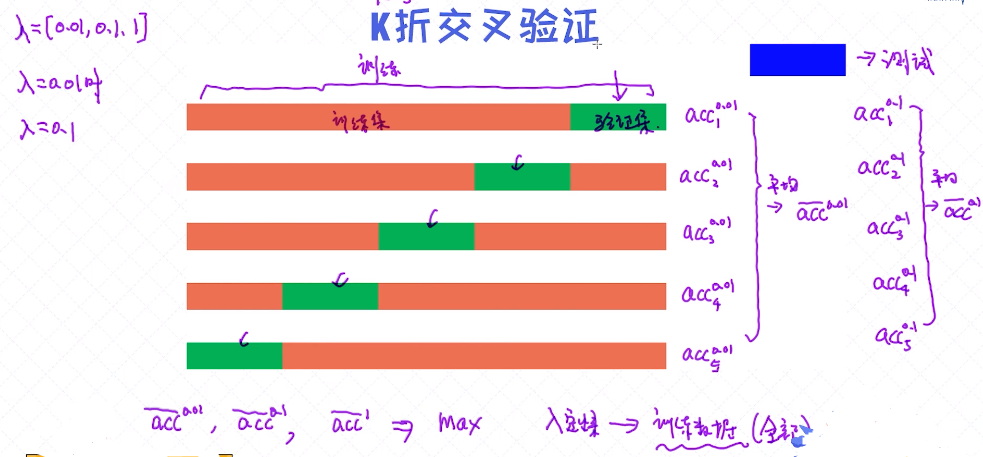
在交叉验证中经常使用K折交叉验证, 就是在已有的数据上重复做多次的验证。为什么需要这么做? 而不是只做一次?
如果只测试一次, 有可能结果中包含偶然性, 但做多次就可以得到比较稳定的结果。
上述K折交叉验证中,我们采用了K=5, 其实K可以取任意的值。问题:什么时候需要取较大的K值?
一般情况下数据量较少的时候我们取的K值会更大,为什么呢? 因为数据量较少的时候如果每次留出比较多的验证数据,对于训练模型本身来说是比较吃亏的,所以这时候我们尽可能使用更多的数据来训练模
型。由于每次选择的验证数据量较少,这时候K折中的K值也会随之而增大,但到最后可以发现,无论K值如何选择,用来验证的样本个数都是等于总样本个数。
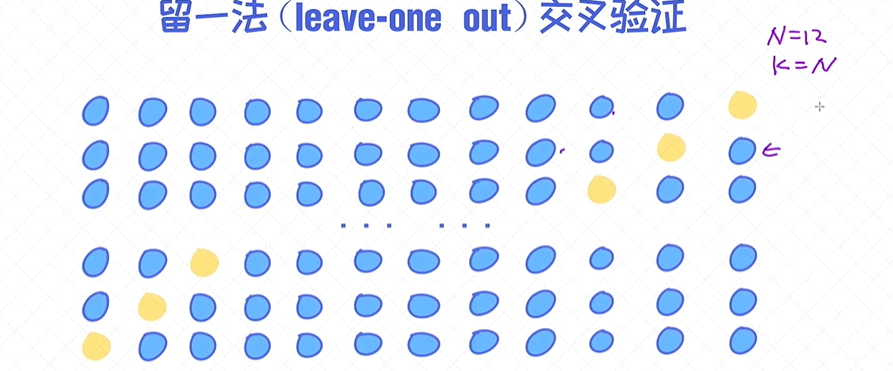
留一法(leave-one out)交叉验证
留一法交叉验证跟k 值交叉验证相比,是一个比较极端的情况,假如有训练数据N=12,k=N,训练数据有多少k 就等于多少;每次训练只把一个样本作为验证集,剩下所有的样本保留为训练集;
每次不同的样本作为一个验证集,循环n 次;
适用于:数据量有限,数据量特别少的情况下;
超参数的设置
对于超参数的取值范围,需要提前设置好。具体设置成什么样的值,其实也要依赖于人的经验。对于每一个经典的机器学习模型, 都有一些参考值可供参考,之后只需从这个范围里搜索出一个最好的即
可。另外,交叉验证的时间复杂度较高,因为需要尝试各种各样的组合。那对于交叉验证如何提升效率呢? 最简单的方法是通过并行化、分布式来解决,因为每一个交叉验证是相互独立的。
对交叉验证的总结
- 1、交叉验证的过程也称之为调参,在AI建模中起到非常关键的作用
- 2、最常用的交叉验证的方法是K折交叉验证,具体K值可以根据数据情况而定
- 3、对于给定的参数组合,交叉验证完全可以并行化
- 4、在做交叉验证时,千万不能使用测试数据来指导模型的训练
- 5、当数据量较少的时候,考虑更大的K值,这样可以确保训练模型时有足够多的数据,一个极端情况是使用留一交叉验证
重要的事情说三遍
- 绝对不能用测试数据来引导模型的训练!
- 绝对不能用测试数据来引导模型的训练!
- 绝对不能用测试数据来引导模型的训练!
4. 正则与先验的关系
相对于最大似然估计的另外一种构建目标函数的方法,叫作最大后验估计,并比较它俩之间的区别。
从最大似然估计到最大后验估计
最大似然估计作为构造目标函数的一种常用方法,广泛地应用在各类机器学习建模中。最大似然估计的核心思想是,给定模型参数的前提下通过最大化观测样本的概率来寻求最优解。从数学的角度来
讲,最大似然估计是最大化p(D∣θ),其中D表示观测到的样本,θ表示模型的参数。
最大后验估计区别于最大似然估计,它最大化的目标函数并不是p(D∣θ),而是p(θ∣D),也就是最大化后验概率。
MLE最大似然估计p(D∣θ),当参数给定的情况下去最大化看到样本的概率;
最大后验概率,是当数据给定的情况下,看到参数的概率;

最大似然估计与最大后验估计
对任何模型都可以从两个不同的维度去构造目标函数,
最大似然估计和最大后验估计它们的区别在于最大后验概率多了一个先验概率。
最大后验概率MAP,P(D)是不变的,通过贝叶斯定理得到 argmax P(D|θ) * P(θ),P(D|θ)是似然概率,P(θ)是先验概率;加入先验概率相当于加入了正则项,也起到防止过拟合的作用;
(先验概率 对这个世界先验的认知,对观察数据的认知);
当数据量比较少的时候,可以适当的使用先验概率;当数据量非常多的时候,先验起到的作用变得越来越小;
先验概率无非是一些分布,比如高斯分布、拉普拉斯分布、迪利克雷分布;选择了高斯分布相当于是加入了L2正则,选择拉普拉斯分布等同于加入了L1正则;
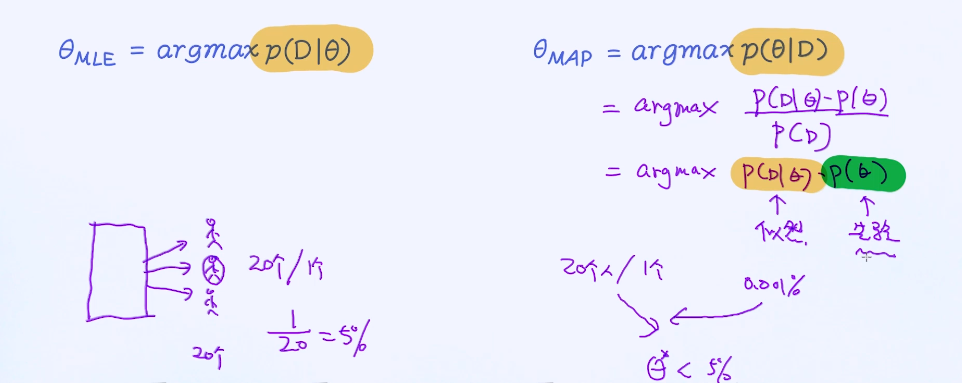
先验与正则之间的关系
总体来讲,MAP要比MLE多出了一个项,就是先验p(θ),这个概率分布是我们可以提前设定好的。这就是MAP的奥妙之处,可以通过先验的方式来给模型灌输一些经验信息;
比如设定参数θ服从高斯分布或者其他类型的分布。不同先验分布和正则之间也有着很有趣的关系:
- 比如先验分布为高斯分布时,对应的为L2正则;
- 当先验设置为拉普拉斯分布时,对应的为L1正则。
把高斯分布的一个假设慢慢变成了L2正则的一个过程;

拉普拉斯分布,假设θ为一维向量,整个的目标函数变成了MLE加上L1正则;

最大后验估计与正则
- ·假设参数的先验概率服从高斯分布,相当于加/入了L2正则!
- ·假设参数的先验概率服从拉普拉斯分布,相当于加/入了L1正则。
最大后验估计趋近于最大似然估计
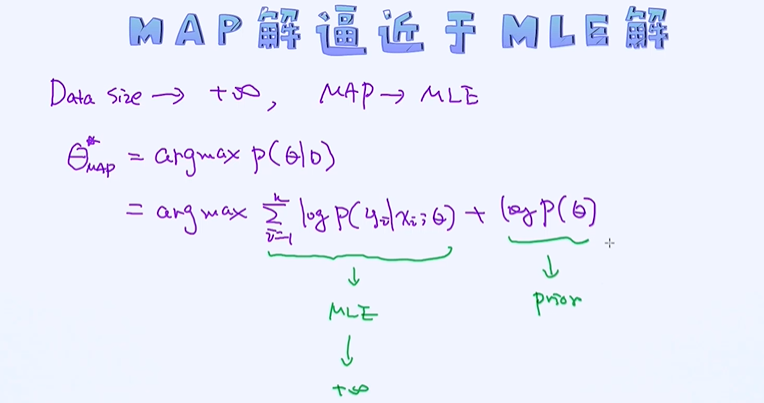
最大似然估计与最大后验估计,当数据量越来越多的时候,最大后验估计逐步逼近于最大似然估计。
最大似然估计和最大后验估计之间也有着特殊的关系:
当数据量无穷多的时候,MAP最大后验估计的结果会逼近于最大似然估计MLE的结果。这就说明,当数据越来越多的时候,先验的作用会逐步减弱。
这个观点放在生活当中也是符合逻辑的。假如我们只有少量的样本,那这时候人的经验必然会占据比较重要的地位,但随着收集到的数据越来越多,数据的作用逐步会超过人的经验,
对后续的决策起到更重要的作用。
5. 案例LR中的调参
如何通过交叉验证来寻找模型最好的超参数。
模型的超参数
对于一个机器学习模型,一般来讲都有一些超参数需要做调整。而且越复杂的模型,它所拥有的超参数类型更多,也增加了交叉验证的复杂度。
支持向量机的调参如下:

随机森林

GridSearchCV的使用
网格搜索交叉验证
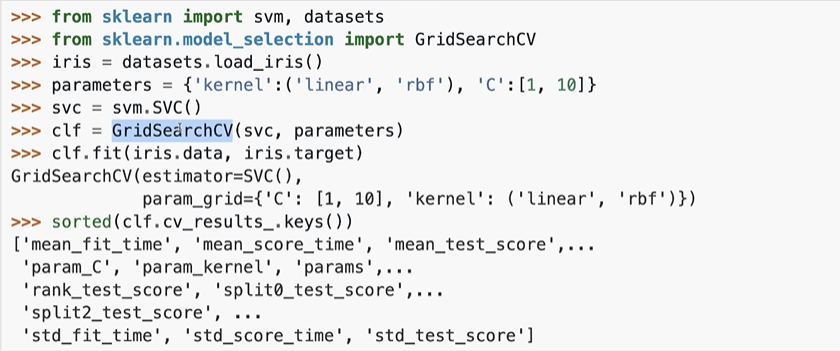
对于模型的调参,Sklearn提供了一个便捷的工具GridSearchCV, 它可以帮助我们很方便地进行交叉验证的工作。 当我们使用GridSearchCV时,只需要告诉它想搜索的每个参数的取值范围即可。
# 导入相应的库
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.model_selection import GridSearchCV
from sklearn import linear_model
# 随机生成样本数据。 二分类问题,每一个类别生成5000个样本数据
np.random.seed(12)
num_observations = 5000
x1 = np.random.multivariate_normal([0, 0], [[1, .75],[.75, 1]], num_observations)
x2 = np.random.multivariate_normal([1, 4], [[1, .75],[.75, 1]], num_observations)
X = np.vstack((x1, x2)).astype(np.float32)
y = np.hstack((np.zeros(num_observations),
np.ones(num_observations)))
print (X.shape, y.shape)
# 数据的可视化
plt.figure(figsize=(12,8))
plt.scatter(X[:, 0], X[:, 1],
c = y, alpha = .4)
from sklearn.linear_model import LogisticRegression
# 构建逻辑回归模型
logistic = linear_model.LogisticRegression(solver='liblinear')
# 惩罚项的类型,考虑两种
penalty = ['l1', 'l2']
# 惩罚项系数可能的取值,考虑10个不同的可能性
C = np.logspace(0, 4, 10)
# 两个参数同时去搜索
hyperparameters = dict(C=C, penalty=penalty)
# 做交叉验证,5折交叉验证,利用已经设置好的hyperparameters
clf = GridSearchCV(logistic, hyperparameters, cv=5, verbose=0)
# 开始训练,做完交叉验证之后,最好的模型存放在best_model中
best_model = clf.fit(X, y)
# 找到最好的超参数
print('Best Penalty:', best_model.best_estimator_.get_params()['penalty'])
print('Best C:', best_model.best_estimator_.get_params()['C'])
====>>
(10000, 2) (10000,)
Best Penalty: l1
Best C: 1.0



 浙公网安备 33010602011771号
浙公网安备 33010602011771号