学习"图"（最短路径）算法

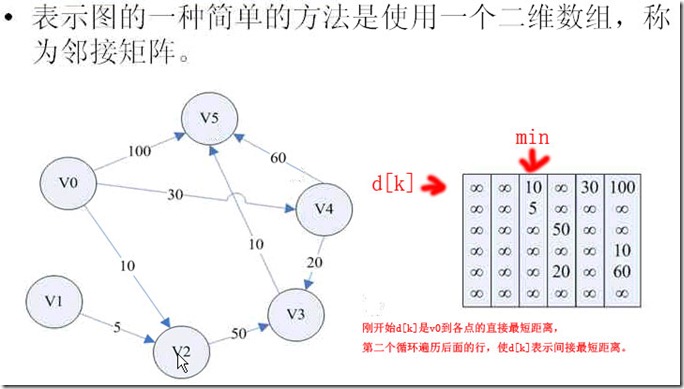
1、首先上图哈：图的邻接矩阵表示。

 

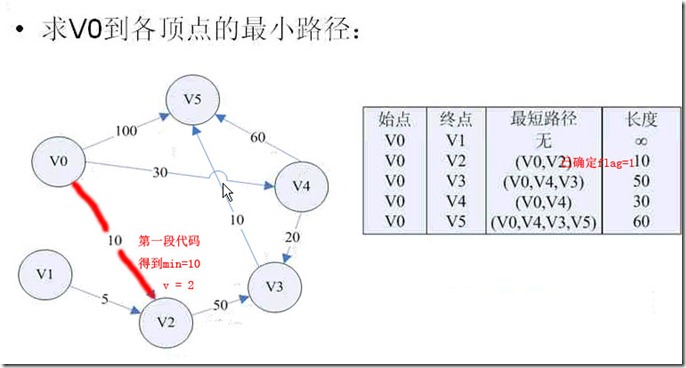
2、图的最短路径

 

#include<stdio.h>

#define MAX 10000
#define N 6

//每个定点到其它顶点的直线距离
int G[N][N]=
{
	{MAX,MAX,10,MAX,30,100},
	{MAX,MAX,5,MAX,MAX,MAX},
	{MAX,MAX,MAX,50,MAX,MAX},
	{MAX,MAX,MAX,MAX,MAX,10},
	{MAX,MAX,MAX,20,MAX,60},
	{MAX,MAX,MAX,MAX,MAX,MAX}
};
//p表示到达这个点的最短距离路径上的节点
int p[N][N] =
{
	//先给他们初始状态
	//v0到v可通的就将其下标存起来
	//v0->v0没意义
	{0,0,0,0,0,0},
	//v0->v1不可通
	{0,0,0,0,0,0},
	//v0->v2可通，
	{0,2,0,0,0,0},
	{0,0,0,0,0,0},
	{0,4,0,0,0,0},
	{0,5,0,0,0,0}
};

void main(){
	//定义距离数组，把求出来的
	//v0到其它点的最短距离都存放在这里。
	int d[N] = {MAX,MAX,10,MAX,30,100};
	//要计算v0到每个点的最短距离
	//方法：遍历除v0之外的所有顶点N遍（最外层i循环），
	//每一遍都找出一个最短距离和经过这个顶点的间接最短距离

	//并且赋值到相应的距离里去。
	//如果能取出比他更短的，否则就以其原来作为最短距离
	int flag[N] = {0};
	int i,v,min,k,j;
	//一共循环N次
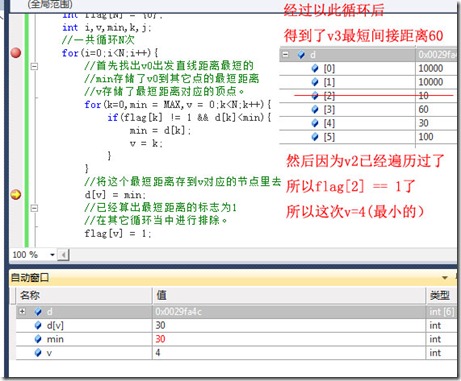
	for(i=0;i<N;i++){
		//首先找出v0出发直线距离最短的
		//min存储了v0到其它点的最短距离
		//v存储了最短距离对应的顶点。
		for(k=0,min = MAX,v = 0;k<N;k++){
			if(flag[k] != 1 && d[k]<min){
				min = d[k];
				v = k;
			}
		}
		//将这个最短距离存到v对应的节点里去
		d[v] = min;
		//已经算出最短距离的标志为1
		//在其它循环当中进行排除。
		flag[v] = 1;

		//开始求间接距离最短
		for(k=0;k<N;k++){
			//还没有求出最短距离，
			//且原来最小的v0到v的直线距离
			//值加上v到k的距离要比直线距离来的小
			//说明d[k] 有更小的了。
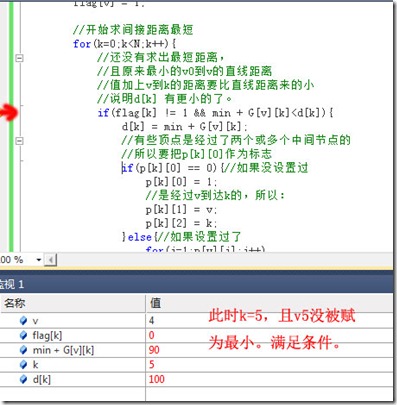
			if(flag[k] != 1 && min + G[v][k]<d[k]){
				d[k] = min + G[v][k];
				//有些顶点是经过了两个或多个中间节点的
				//所以要把p[k][0]作为标志
				if(p[k][0] == 0){//如果没设置过
					p[k][0] = 1;
					//是经过v到达k的，所以：
					p[k][1] = v;
					p[k][2] = k;
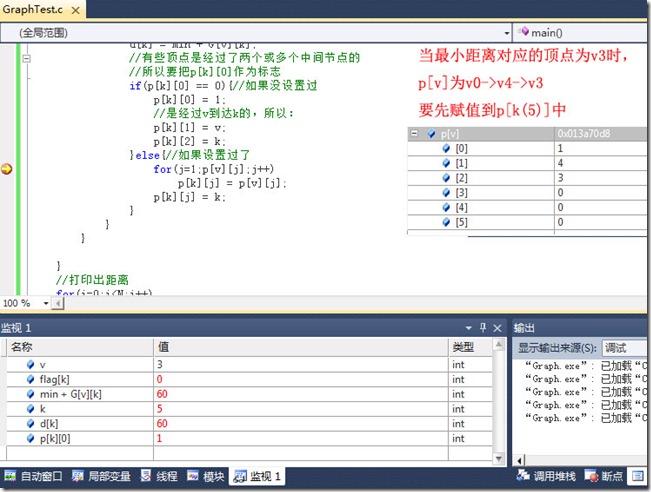
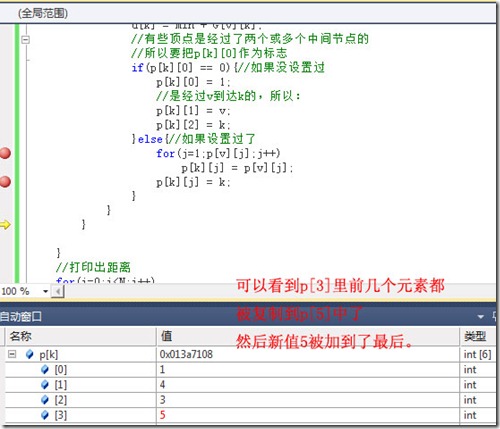
				}else{//如果设置过了
					for(j=1;p[v][j];j++)
						p[k][j] = p[v][j];
					p[k][j] = k;
				}
			}
		}

	}
	//打印出距离
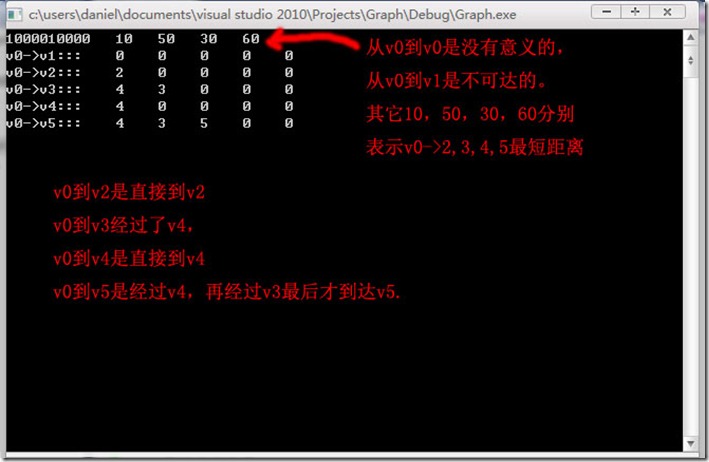
	for(i=0;i<N;i++)
		printf("%5d",d[i]);
	printf("\n");
	//打印最短距离经过的节点
	for(i=1;i<N;i++){
		printf("v0->v%d:::",i);
		for(j=1;j<N;j++)
			printf("%5d",p[i][j]);
		printf("\n");
	}
	getchar();
}

我们可以看下运行的结果

是不是还不理解外层循环到底做了什么？

v到底变了没有？

让我们来调试一下：

 

现在来看看下面的一个for(k)是干什么的。。

大功告成！OK。。。