Transformer Position Encoding

Reference:
https://kikaben.com/transformers-positional-encoding/
https://machinelearningmastery.com/a-gentle-introduction-to-positional-encoding-in-transformer-models-part-1/

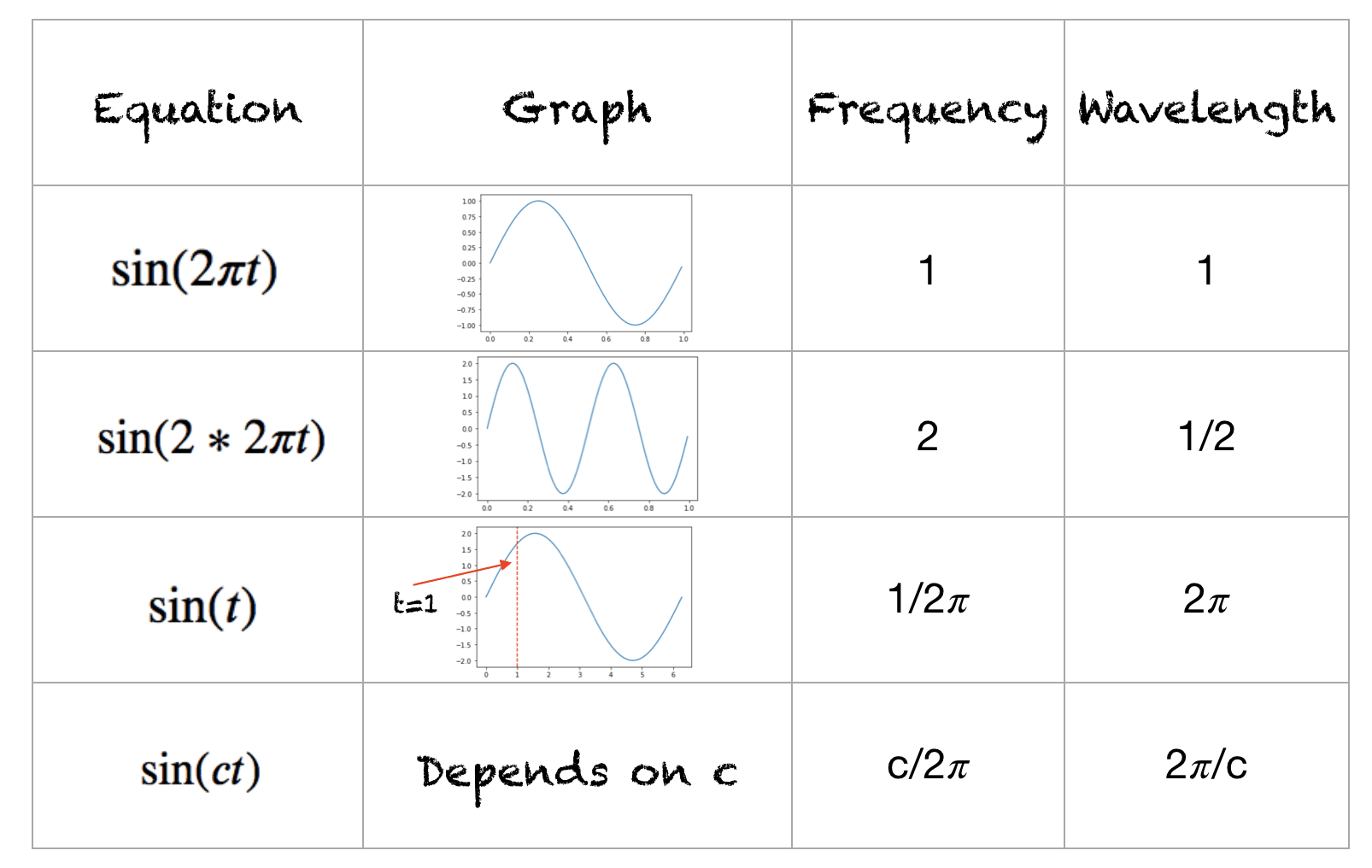
1. Why Positional Encoding?

Without positional information, an attention-only model might believe the following two sentences have the same semantics:

Tom bit a dog.

A dog bit Tom.

There are many reasons why a single number, such as the index value, is not used to represent an item’s position in transformer models.

For long sequences, the indices can grow large in magnitude.

If you normalize the index value to lie between 0 and 1, it can create problems for variable length sequences as they would be normalized differently.

2. Why element-wise addition instead of concatnation?

1. It increases the memory footprint, and training will likely take longer as the optimization process needs to adjust more parameters due to the extra dimensions.
2. If reduce Positional Encoding dimensions, there will be another hyper-parameter to tune.
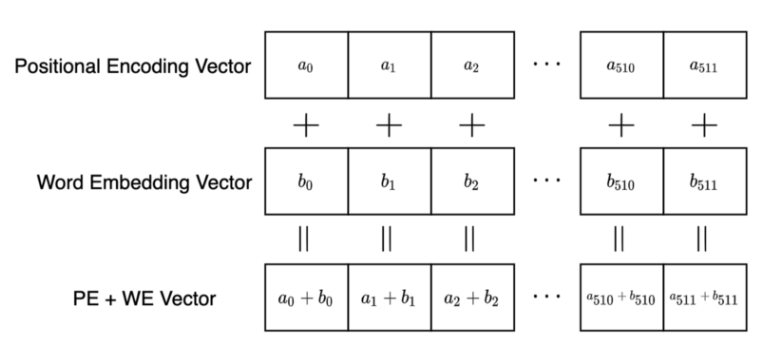
   So, the Positional Encoding and Word Embedding have the same dimensions , so we can sum a word embedding vector and a positional encoding vector by element-wise addition:
   

3. How To Encode Word Positions?

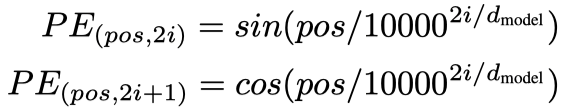
where pos is the position and i is the dimension. That is, each dimension of the positional encoding corresponds to a sinusoid. The wavelengths form a geometric progression from 2π to 10000 · 2π.

Since we have 512 dimensions, we have 256 pairs of sine and cosine values. As such, the value of i goes from 0 to 255.
For specified position(word), 512 embedding values should like this:

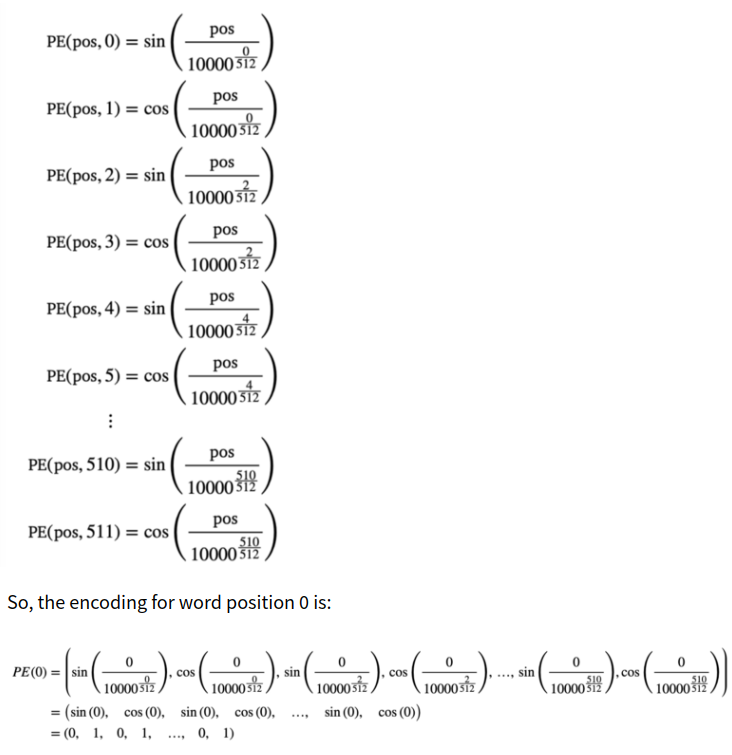
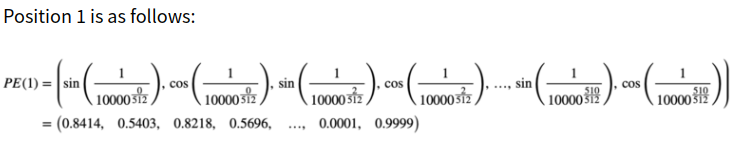
4. Visualize Positional Encoding

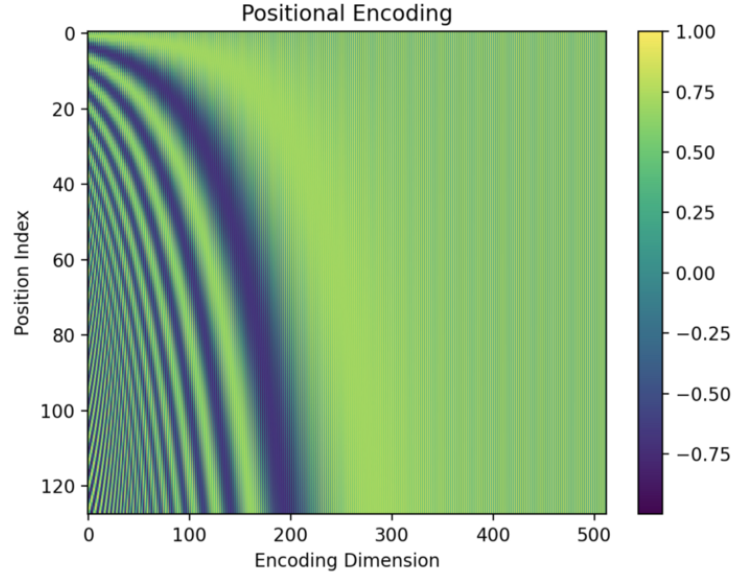
As expected, the values towards the right (the end of vector elements) seem to have alternating 0s (dark green) and 1s (yellow). But it’s hard to see due to fine pixels.
So, I created a smaller version of the encoding matrix with the max length = 16 and the d_model = 32.

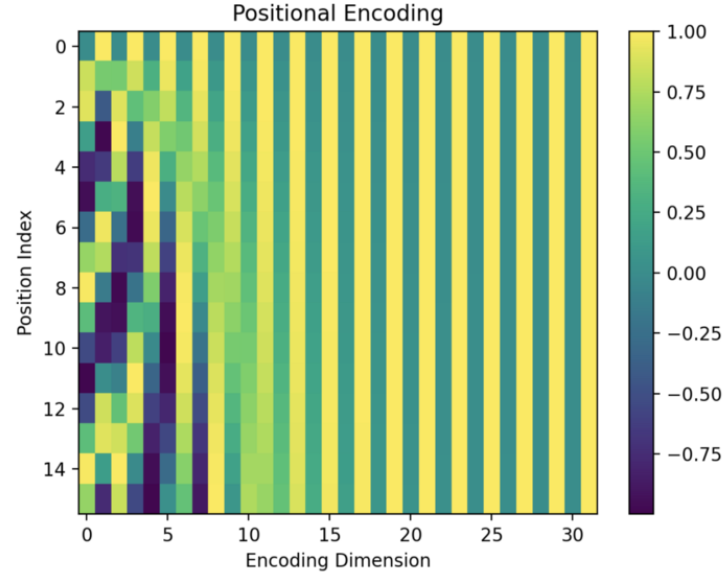
5. How To Interpret Positional Encoding (genius!)?

Position Encoding

Positional encoding has pairs of sine and cosine functions. If we take any pair and plot positions on a 2D plane, they are all on a unit circle.

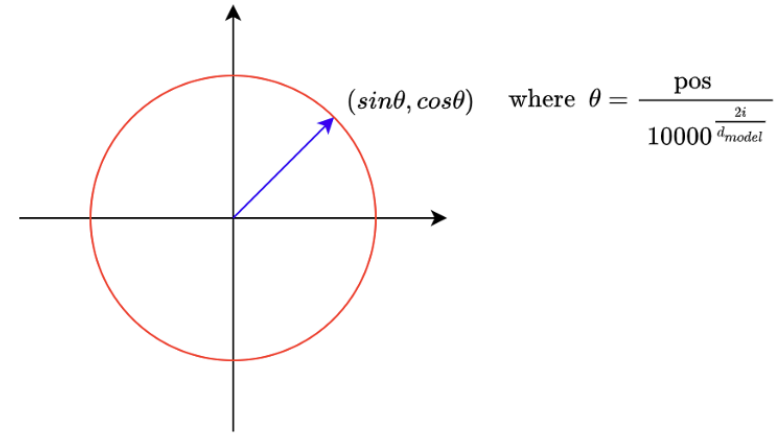
When we increase the value pos, the point moves clockwise. It’s like a clock hand that moves as word position increases. In a positional encoding vector with 512 dimensions, we have 256 hands.
So, we can interpret positional encoding as a clock with many hands at different speeds. Towards the end of a positional encoding vector, hands move slower and slower when increasing position index (pos).

So, we can think of each position having a clock with many hands pointing to a unique time.

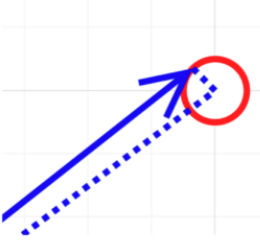
The combination of positional encoding and word embedding

If we take the first two dimensions of a word embedding vector as a point(x, y), we can draw it in a 2D plane:

Adding the first two dimensions of a positional encoding to this will point somewhere on a unit circle around the word embedding. (All vectors start at [0, 0])

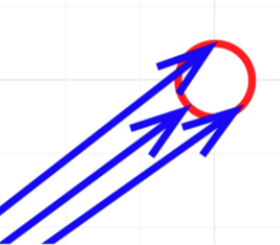
How does the model distinguish between word embeddings and positional encodings?

The word embedding layer has learnable parameters, so the optimization process can adjust the magnitudes of word embedding vectors if necessary.

I'm not saying that is indeed happening, but it is capable of that. It is amazing that the model somehow learns to use the word embeddings and the positional encodings without mixing them up.

The power of optimization is incredible.

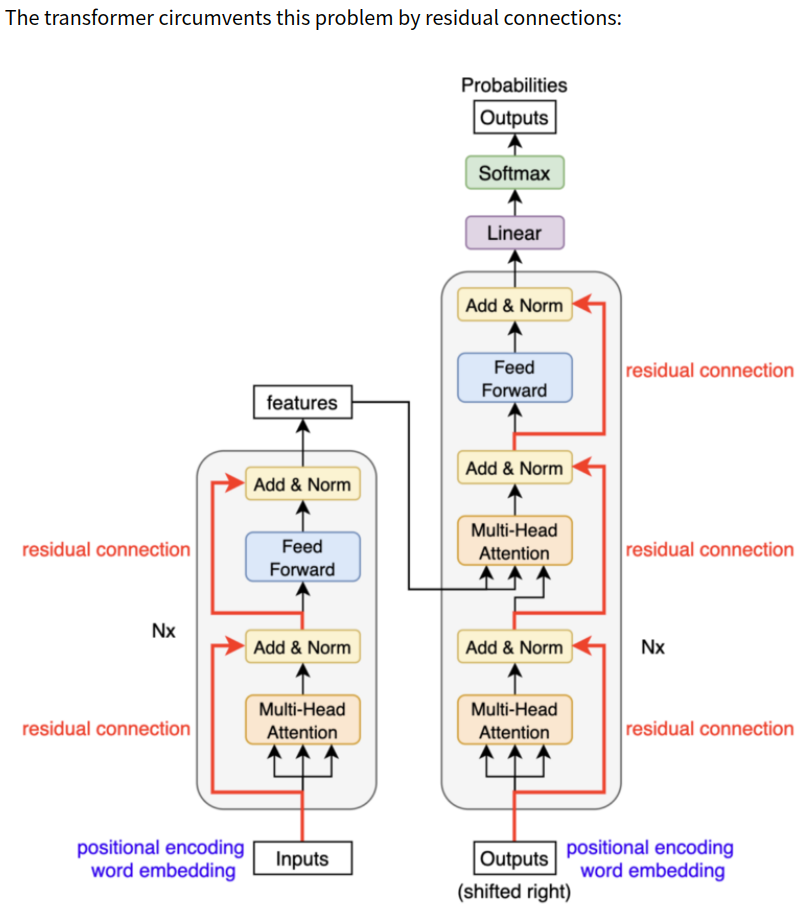
6. How Positions Survive through Multiple Layers?