指数族分布
原博客作者:TsReaper
原博客链接:https://www.cnblogs.com/tsreaper/p/exp-family.html
原博客公式全显示为LaTex代码,我临时复制过来显示公式
为什么需要指数族分布
机器学习经常要做这样一件事:给定一组训练数据 D,我们希望通过 D 得到我们研究的空间的概率分布。这样,给出一个测试数据,我们就可以找出条件概率中概率最大的那个点,将其作为答案输出。
但是在没有任何假设的情况下,直接学习概率分布是不现实的。直接学习概率分布最简单的方法,就是把空间分成很多很多小的单元,然后统计样本落在每个单元的频率,作为每个单元的概率分布。但是这种方法会面临着数据不足、有噪音、存储能力受限等问题。单元分隔得越细,学习到得概率分布就越准确,但是我们就需要越多的数据来训练,也需要越多的存储空间来存储(一维的时候存储 $n$ 个单元,二维就要 $n^2$,三维就要 $n^3$...),这样的方法对于高维数据来说是绝对不可行的。
所以在大多数情况下,我们都会人为指定某种概率分布的形式(例如指定为高斯分布或伯努利分布等)。这样,对概率函数的学习就转化为了函数参数的学习,减小了学习的难度;我们也只需要存储我们感兴趣的统计量(例如对于高斯分布,我们只需要存储均值和方差;对于伯努利分布,我们只需要存储取正类的概率),减小了对存储空间的需求。当然,由于人为限定了概率分布形式,我们就需要根据不同的问题选择不同的分布,就像对不同问题选择不同的机器学习模型一样。
指数族分布就是一类常用的分布模型,它有很多优良的性质。接下来我们介绍指数族分布的推导和性质。
指数族分布的推导
我们用离散模型介绍指数族分布的推导,连续模型的推导也类似。
设 $X^{(i)}$ 表示第 $i$ 条训练数据,$\phi(X^{(i)})$ 表示从第 $i$ 条训练数据中我们感兴趣的统计量(是一个向量,这样我们就可以表示两个或者更多我们感兴趣的统计量)。我们希望我们的概率模型 $p$ 能满足以下性质 $$\mathbb{E}_p[\phi(X)] = \hat{\mu}$$ 其中 $$\hat{\mu} = \frac{1}{n}\sum_{i=1}^m\phi(X^{(i)})$$ 简单来说,就是概率模型的期望等于所有训练数据的均值,这个希望应该是非常合理的。
但满足这个条件的概率模型有很多种,我们再加一条限制:这个概率模型要有最大的信息熵,也就是有最大的不确定性。我们认为这样的概率模型能够涵盖更多的可能性。
根据信息熵的定义,我们写出以下式子 $$p^*(x) = \mathop{\text{argmax}}\limits_{p(x)} \quad -\sum_x p(x)\log p(x) \\ \begin{matrix} \text{s.t.} & \sum\limits_x \phi(x)p(x) = \hat{\mu} \\ & \sum\limits_x p(x) = 1 \end{matrix}$$ 这是一个有等式限制的优化问题,用拉格朗日乘子法改写为 $$L = -\sum_x p(x)\log p(x) + \theta^T(\sum_x \phi(x)p(x) - \hat{\mu}) + \lambda(\sum_x p(x) - 1) \\ = \sum_x (-p(x)\log p(x) + \theta^T\phi(x)p(x) + \lambda p(x)) - \theta^T\hat{\mu} - \lambda$$ 对 $x$ 取每一个特定值时的 $p(x)$ 分别求导,我们有 $$-1-\log p(x) + \theta^T\phi(x) + \lambda = 0$$ 移项后有 $$p(x) = \exp(\theta^T\phi(x) + \lambda - 1) = \exp(\theta^T\phi(x) - A)$$ 式子两边关于 $x$ 求和有 $$\sum_x p(x) = 1 = \sum_x \exp(\theta^T\phi(x) - A)$$ 移项后就有 $$A(\theta) = \log\sum_x \exp(\theta^T\phi(x))$$ 要注意的是,$A$ 是一个关于 $\theta$ 的函数,和 $x$ 的取值无关。
使用指数族分布
根据上面的推导,我们就得到了指数族分布的模型:$p(x) = \exp(\theta^T\phi(x) - A(\theta))$。这个模型虽然看起来和之前的博客中介绍的指数族模型($p(x) = b(x)\exp(\theta^T\phi(x) - A(\theta))$)不太一样,但我们可以让 $\theta'^T = \begin{bmatrix} \theta^T & 1 \end{bmatrix}$ 以及 $\phi'(x) = \begin{bmatrix} \phi(x) & \log b(x) \end{bmatrix}^T$ 将它变化为这篇博客中介绍的形式,只不过有的时候把 $b(x)$ 单独提出来更方便。
我们看到的大部分分布都能满足指数族分布的形式。比如令 $\theta^T = \begin{bmatrix} \log\phi & \log(1-\phi) \end{bmatrix}$,$\phi(x) = \begin{bmatrix} x & 1-x \end{bmatrix}^T$,$A(\theta) = 0$ 就有伯努利分布 $p(x) = \phi^x(1-\phi)^{1-x}$;比如令 $b(x) = 1 / \sqrt{(2\pi)^k|\Sigma|}$,$\theta^T = \begin{bmatrix} -\frac{1}{2}\mu^T\Sigma^{-1} & \Sigma^{-1} \end{bmatrix}$,$\phi(x) = \begin{bmatrix} x & xx^T \end{bmatrix}^T$,$A(\theta) = 0$ 就有多维高斯分布(这时候把 $b(x)$ 单独提出来就比较方便)。
我们还有 $\theta$ 的值没有确定。理论上,我们应该根据拉格朗日乘子法求出 $\theta$ 的值,但这样求是比较困难的。就像之前的博客写的一样,我们可以通过极大似然估计法计算 $\theta$ 的值。而且我们可以证明,用极大似然估计法算出的 $\theta$,可以满足 $\mathbb{E}_p[\phi(X)] = \hat{\mu}$ 的要求。
对训练数据集 D 使用极大似然估计法,其实就是解如下优化问题 $$\mathop{\text{argmax}}\limits_{\theta} \quad L \\ = \mathop{\text{argmax}}\limits_{\theta} \quad p(D|\theta) \\ = \mathop{\text{argmax}}\limits_{\theta} \quad \sum_{i=1}^m (\theta^T\phi(X^{(i)}) - A(\theta))$$ $L$ 关于 $\theta$ 求偏导有 $$\frac{\partial L}{\partial \theta} = \sum_{i=1}^m \phi(X^{(i)}) - n\frac{\partial A(\theta)}{\partial \theta} = 0 $$ 求得 $$\frac{\partial A(\theta)}{\partial \theta} = \hat{\mu}$$ 根据之前的推导我们有 $$A(\theta) = \log\sum_x\exp(\theta^T\phi(x))$$ 所以 $$\frac{\partial A(\theta)}{\partial \theta} = \frac{\sum\limits_x \exp(\theta^T\phi(x))\phi(x)}{\sum\limits_x \exp(\theta^T \phi(x))} = \frac{\sum\limits_x \exp(\theta^T\phi(x))\phi(x)}{\exp A(\theta)} \\ = \sum_x \exp(\theta^T\phi(x) - A(\theta))\phi(x) = \mathbb{E}_p[\phi(x)]$$ 所以 $\mathbb{E}_p[\phi(X)] = \hat{\mu}$ 的条件是满足的。
指数族分布与贝叶斯学派
我们知道,机器学习可以分为频率学派和贝叶斯学派。频率学派认为概率分布的 $\theta$ 是一个已知的确定值(只是我们还不知道),尝试通过各种方法直接建立概率分布模型并优化 $\theta$ 的值;而贝叶斯学派认为,$\theta$ 的值并不是固定的,而是和“人”的认知是有关的。
贝叶斯学派认为 $\theta$ 也是随机变量,一个人一开始对 $\theta$ 分布的认知就是先验概率分布,在他观察过训练数据之后,他对 $\theta$ 的认知会发生改变,这时的概率分布就是后验概率分布。
贝叶斯学派最重要的公式之一就是贝叶斯公式 $$p(\theta|D) = \frac{p(\theta)p(D|\theta)}{p(D)}$$ 其中 $p(\theta)$ 就是观察训练数据之前对 $\theta$ 原始的认知,就是先验概率;而 $p(\theta|D)$ 则是观察训练数据之后对 $\theta$ 的认知,就是后验概率。而 $p(D|\theta)$ 和 $p(D)$ 就是训练数据带给“人”的信息。式子两边取对数,公式可以变化为 $$\log p(\theta|D) = \log p(\theta) + \log p(D|\theta) + \text{const}$$ 常数的大小无关紧要,因为最后我们只需要选择让 $p(\theta|D)$ 最大的 $\theta$ 即可,而对于所有 $\theta$ 来说,这个常数是一样大的,不影响比较。这个公式告诉我们,后验知识 = 先验知识 + 数据认识,也可以说,数据帮助“人”修正认知。
如果假设测试数据服从和 $\theta$ 有关的指数族分布,那么我们有 $$\log p(D|\theta) = \theta^T\sum_{i=1}^m\phi(X^{(i)}) - A(\theta)$$ 可是先验概率分布是怎么样的呢?现在贝叶斯学派的研究,大多都会构造一个先验概率分布。这个构造的分布在复杂情况下主要用于消除 $\log p(D|\theta)$ 中一些比较麻烦的项。的确,应该要按问题的性质构造先验概率分布比较合理,但是这样概率分布的式子可能会变得很复杂,无法在有限时间内计算。这种不按问题性质而构造先验概率分布的方法也是当前贝叶斯学派比较受诟病的一点。
既然数据认识是一个指数族分布,我们也构造一个指数族分布的先验概率分布,便于计算。我们构造 $\log p(\theta) = \eta^T \begin{bmatrix} \theta & A(\theta) \end{bmatrix}^T + \text{const}$,将 $\log p(\theta)$ 与 $\log p(D|\theta)$ 代入式子后,我们有 $\log p(\theta|D) = \eta'^T \begin{bmatrix} \theta & A(\theta) \end{bmatrix}^T + \text{const}$,其中 $\eta' = \eta + \begin{bmatrix} \sum_{i=1}^m \phi(X^{(i)}) & -1 \end{bmatrix}^T$。也就是说,我们关注的统计量是 $\theta$ 和 $A(\theta)$,而每看到一组训练样本,我们只要更新 $\eta$ 就能将先验分布改为后验分布。这是我们先验分布选择了一个方便计算的形式的结果。
来举一个例子:现在有一枚硬币,投掷了若干次,其中 $g$ 次正面朝上,$h$ 次反面朝上。希望拟合出一个参数为 $\theta$ 的伯努利分布,作为投硬币的概率模型。
根据之前的推导,我们有 $\log p(D|\theta) = \sum_{i=1}^m(X^{(i)}\log\theta + (1-X^{(i)})\log(1-\theta))$。现在我们想获得的是 $\theta$ 的概率分布,所以我们关注的统计量应该是 $\begin{bmatrix} \log\theta & \log(1-\theta) \end{bmatrix}^T$,那么构造先验分布 $\log p(\theta) = \begin{bmatrix} a & b \end{bmatrix}\begin{bmatrix} \log\theta & \log(1-\theta) \end{bmatrix}^T + \text{const}$(因为 $A(\theta) = 0$ 所以我们这里就省略了这一维)。这样,先验分布就是 $p(\theta) = C\theta^a(1-\theta)^b$,后验分布就是 $p(\theta|D) = C\theta^{a+g}(1-\theta)^{b+h}$,是两个 beta 分布。
非常恰好的是,这两个分布具有很高的可解释性。我们画出几个 beta 分布的图像。
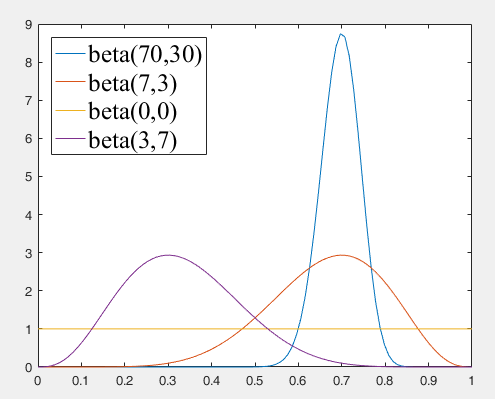
beta(0, 0) 可以看作训练最开始的先验概率,没有见过任何训练数据,所以认为所有的 $\theta$ 都是等概率的;beta(7, 3) 和 beta(3, 7) 可以看作抛硬币 10 次后的后验概率,可以看到 beta 分布的峰值分别出现在 0.7 和 0.3 处,但是方差较大,没有那么肯定;beta(70, 30) 可以看作抛硬币 100 次后的后验概率,可以看到 beta 分布的峰值出现在 0.7 处,而且方法很小,说明此时我们非常肯定 $\theta = 0.7$ 是最佳的参数。
当然,这种可解释性是非常凑巧的。在比较复杂的问题中,这种构造出来的先验分布基本是没有解释性的。而且如果训练数据量太小,最后的后验概率受先验概率的影响会很大,可能会出现变形的结果。一个又符合问题特征,又便于计算的先验分布是非常难获得的,所以现在的贝叶斯学派只能暂时以可计算性为重。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号