球形空间产生器

题目

一道推式子然后高斯消元的题,难度并不大

首先知道一件事,在\(n\)维空间中我们将一个点\(x\)表示为\(x(x_1,x_2,x_3,...,x_n)\)
那么对于另外一点\(a(a_1,a_2,a_3,...,a_n)\)
\(x->a\)距离为:

\(dis =\sum_{i=1}^n(x_i-a_i)^2\)

设球心为\(x(x_1,x_2,x_3,...,x_n)\),抓住球心到球上所有点的距离相等,我们可以列出若干个二次方程,然后再简单的消元得到了\(n\)个一次方程,这时候我们就可用高斯消元解决这个问题了

接下来是我在希沃上的推理,书写比较张狂

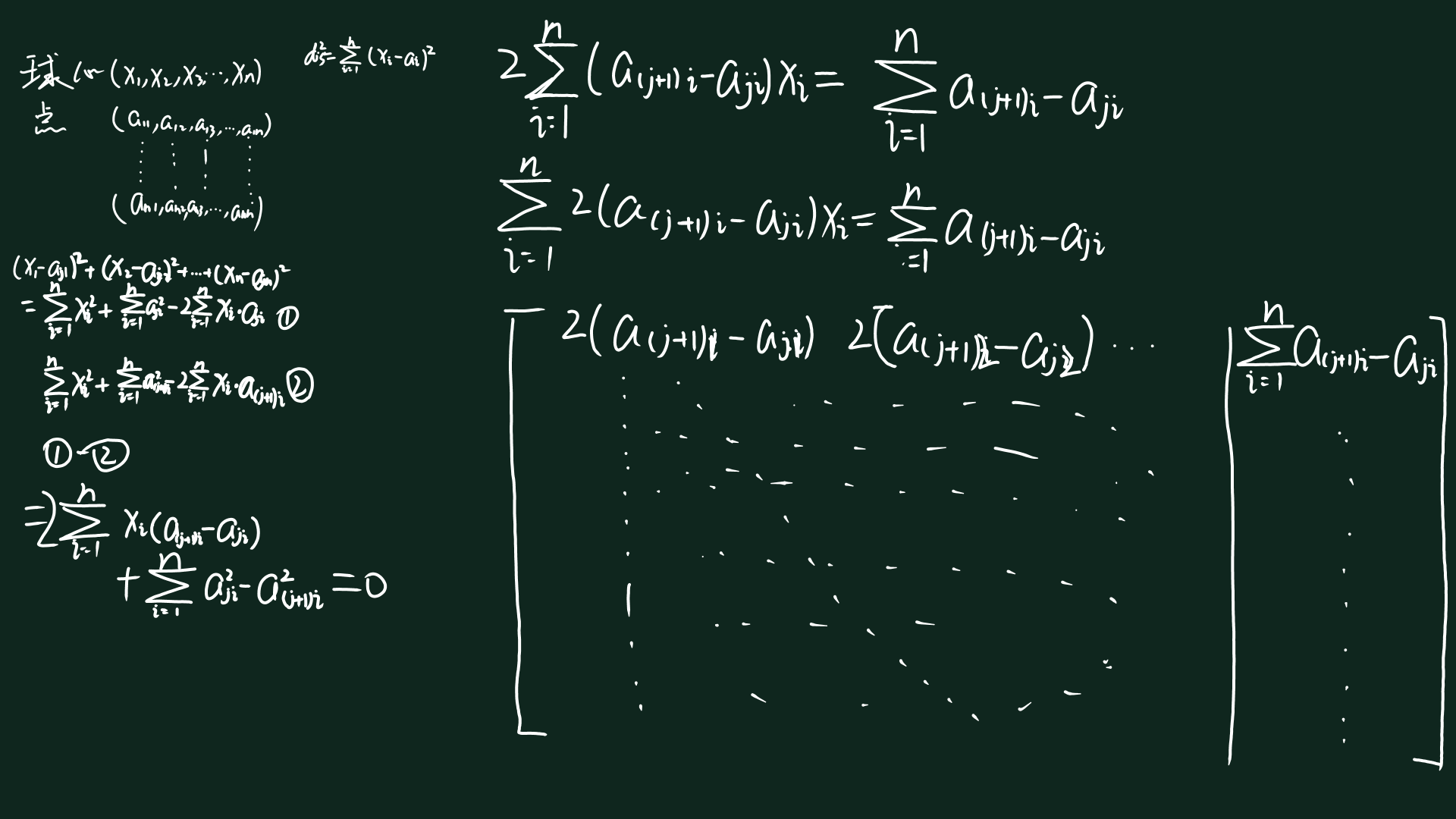
总的来说,这题的难度并不大,如果你要使用模拟退火这种奇技淫巧玄学做法,正确率反而不行