拉格朗日插值

题目链接

题目大意 : 给定 \(n+1\) 个点 \((x_i,y_i)\) , 这些点可以确定一个 \(n\) 次的多项式 \(f(x)\) 求\(f(k)\mod{998244353}\)

方法1 : 使用高斯消元(我不会hh) 复杂度\(O(n^3)\),不够看
方法2 : 拉格朗日插值法

0x01 拉格朗日基本多项式(多项式基函数)

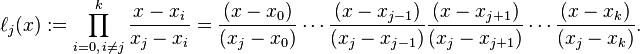
0x02 拉格朗日插值多项式

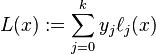
0x03 验证 : 这个多项式恰好过给定的 \(n+1\) 个点

考虑将每个\(x_i\)带入\(ℓ(x)\)中,会发现除了\(ℓ_i(x)=1\)外,其它的基函数值都为\(0\),那么此时\(L(x)\)的值就是\(y_i\) , 满足正确性

0x04 关于这道题

显然要求一下逆元,可以把分母先乘起来再用费马小定理求逆元，就不会卡时了,时间复杂度\(O(n^2)\)

\(code\)

#include <bits/stdc++.h>
using namespace std;
inline int read(){
	char ch=getchar();
	int s=0,f=1;
	for(;!isdigit(ch);ch=getchar()) if(ch=='-') f*=-1;
	for(; isdigit(ch);ch=getchar()) s*=10,s+=ch-'0';
	return s*f;
}
const int N = 2e3+10;
const int mod = 998244353;
typedef long long ll;
inline ll qp(ll x,ll y){
	ll s=1;
	while(y){
		if(y&1) s=s*x%mod;
		x=x*x%mod;
		y>>=1;
	}
	return s;
}
inline ll inv(ll x){
	return qp(x,mod-2);
}
int x[N],y[N],n,k;
ll s1,s2,ans;
int main(){
	n=read(),k=read();
	for(int i=1;i<=n;i++)
		x[i]=read(),y[i]=read();
	for(int i=1;i<=n;i++)
    {
        s1=y[i] % mod;s2 = 1ll;
        for(int j=1;j<=n;j++)
        	if(i!=j)
        		s1 = s1 * (k - x[j]) % mod,s2 = s2 * ( (x[i] - x[j] % mod) % mod) % mod;
        ans+=s1*inv(s2)%mod;ans=(ans+mod)%mod;
    }
    printf("%lld\n",ans);
	return 0;
}

0x05 Extra1 当点坐标\(x\)连续时候的写法

\(x\)为$ 1-(n+1) $,就是求这个

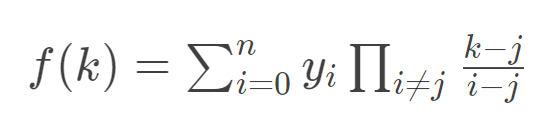
对于分子可以考虑维护出关于\(k\)的前缀积和后缀积

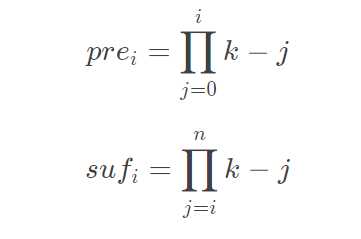
对于分母,发现可以表示为\(i!(-1)^{n-i}（n-1)!\)
把他们都预处理出来,时间复杂度将为 \(O(n)\)