反射容斥优化 DP 简介

推歌

《春风来》

作者：阿良良木健

正文

P1641 [SCOI2010]生成字符串

题意

对于一个数列 \(A=\{a_i|i\in[1,n+m]\cap\N\}\)，若 \(\forall i\in [1,n+m],(a_i=0\lor a_i=1)\land \sum_{j=1}^i[a_j=0]\le\sum_{j=1}^i[a_j=1]\)，且 \(\sum_{i=1}^{n+m}[a_i=0]=m\land\sum_{i=1}^{n+m}[a_i=1]=n\)，则称 \(A\) 是一个数列。给出 \(n,m\)，求合法数列数量。保证 \(1\le m\le n\le 10^6\)。

思路

考虑朴素的 DP。令 \(f_{i,j}\) 表示前 \(i+j\) 个数中选 \(i\) 个 \(1\) 和 \(j\) 个 \(0\) 的方案数，显然就有 \(f_{i,j}=[i\ge j]\times(f_{i-1,j}+f_{i,j-1})\)。边界条件为 \(f_{0,0}=1\)，答案为 \(f_{n,m}\)。我们观察这个式子，发现如果去掉限制条件，这个 DP 就是描述从点 \((0,0)\) 每次往右走 \(1\) 或往上走 \(1\) 走到 \((n,m)\) 的总方案数。那么加上这个限制之后这个方程在描述什么呢？显然，就是走的过程中不能走到坐标有纵坐标比横坐标大的点。容易发现这些点就是函数 \(y=x\) 上方的所有点（不包括该函数上的点）。又因为只能走整点，所以把 \(y=x\) 向上平移 \(1\) 个单位得到 \(y=x+1\)，这些点就是函数 \(y=x+1\) 上方所有点（包括该函数上的点）。如下图：

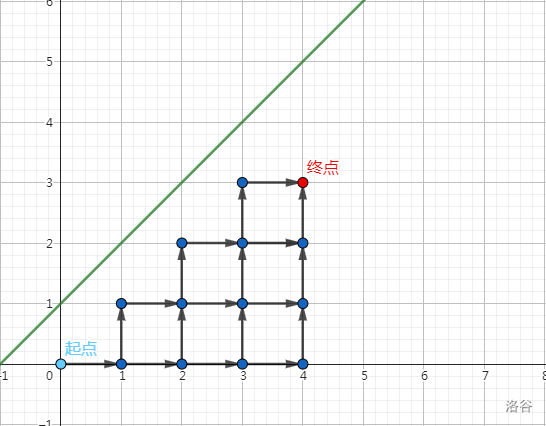
那我们就要求走的过程中不经过 \(y=x+1\)。容易想到方案数就是不做要求的方案数减去经过 \(y=x+1\) 的方案数。这是一个基础的容斥。

不做要求的方案数是很好求的。我们总共要走 \(n+m\) 步，其中 \(n\) 步是在横坐标上走，答案就是 \({n+m}\choose n\)。经过 \(y=x+1\) 的方案数怎么求呢？既然经过就一定有第一次经过。我们把第一次经过 \(y=x+1\) 前的点都沿 \(y=x+1\) 做轴对称。如下图：

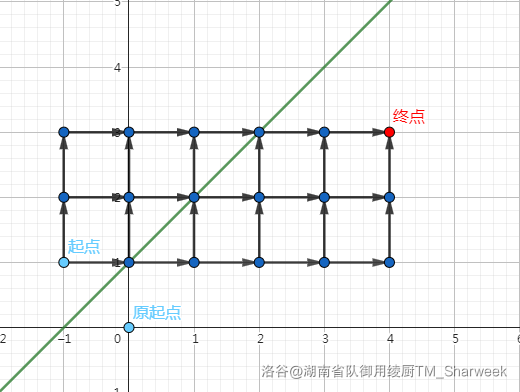
向上走对称过去成了向右走，向右走成了向上走，起点对称过去成了 \((-1,1)\)。容易发现，从 \((-1,1)\) 到 \((n,m)\) 的路径集合与经过 \(y=x+1\) 的路径集合形成了一个双射：把第一次 \(y=x+1\) 前的步数全部做一个轮换 \((向上走,向右走)\)（即把向上走变成向右走，向右走变成向上走）。所以这两个集合大小也相等。所以经过 \(y=x+1\) 的方案数就是从 \((-1,1)\) 到 \((n,m)\) 的方案数，即 \({n+m}\choose{n+1}\)。该题答案即为 \({{n+m} \choose {n}} - {{n+m} \choose {n+1}}\)。

特别的，当 \(n=m\) 时，计算结果就是 Catalan 数列的第 \(n\) 项。

代码

/*********************************************************************
    程序名:
    版权:
    作者: TM_Sharweek
    日期: 2025-02-21 15:42
    说明:
*********************************************************************/
#include <bits/stdc++.h>

#define p_b push_back
#define m_p make_pair
#define sec second
#define fst first
#define p_q priority_queue
#define u_m unordered_map

using namespace std;

using ll = long long;
using ull = unsigned long long;
using i128 = __int128;

const int N = 2e6 + 50;
const ll P = 20100403;

ll qpow(ll a, ll x) {
	a %= P;
	ll ans = 1;
	while (x) {
		if (x % 2)
			ans = ans * a % P;
		a = a * a % P;
		x >>= 1;
	}
	return ans;
}

ll inv(ll x) {
	return qpow(x, P - 2);
}

ll jc[N];

ll C(int n, int m) {
	return jc[m] * inv(jc[n]) % P * inv(jc[m - n]) % P;
}

int main() {
//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	int n, m;
	cin >> n >> m;
	jc[0] = 1;
	for (int i = 1; i <= n + m; i++)
		jc[i] = jc[i - 1] * i % P;
	cout << (C(n, n + m) - C(n + 1, n + m) + P) % P << endl;

	return 0;
}

P3266 [JLOI2015] 骗我呢

题意

给出 \(n,m\)，求大小为 \(n\times m\) 的满足下列条件的矩阵 \(A=\{a_{i,j}\}\) 个数：

• \(\forall i\in[1,n]\cap\N,j\in[1,m]\cap\N,a_{i,j}\in[0,m]\cap\N\)。
• \(\forall i\in[1,n]\cap\N,j\in[1,m-1]\cap\N,a_{i,j}<a_{i,j+1}\)。
• \(\forall i\in[2,n]\cap\N,j\in[1,m-1]\cap\N,a_{i,j}<a_{i-1,j+1}\)。

对 \(10^9+7\) 取模，\(1\le n,m\le 10^6\)。

思路

注意到 \(a_{i,j}\) 的值域和一行元素的个数相关，与此同时，\(A\) 中每一行分别单调递增。也就是说，\(A\) 的每一行都一定是 \(0\) 至 \(m\) 中删去一个元素后排序的值。那么 \(A\) 的一行可以直接由它删去的元素决定。所以我们可以考虑设 \(f_{i,j}\) 表示考虑前 \(i\) 行，第 \(i\) 行少的元素是 \(j\)。怎么转移呢？我们先考虑如何通过少的元素 \(j\) 来确定第 \(i\) 行。对于整数 \(k\)，如果 \(0\le k-1<j\) 的话，显然就有 \(a_{i,k}=k-1\)，因为 \(0\) 至 \(j-1\) 的元素都有，所以前 \(j\) 个元素一定就是 \(0\) 到 \(j-1\)；如果 \(j+1\le k\le m\)，那么 \(a_{i,k}\) 就应该是 \(k\)，因为 \(j+1\) 到 \(m\) 也一定都有，所以后 \(m-j\) 个元素一定是 \(j+1\) 到 \(m\)。

我们已经将前两条限制做到了，考虑第三条限制。第三条限制要求 \(a_{i,k}<a_{i-1,k+1}\)。我们考虑把它转换为对每行没有的元素的约束。设第 \(i\) 行没有的元素为 \(j\)，第 \(i-1\) 行没有的为 \(j'\)。我们发现第 \(i\) 行不选 \(j\) 正相当于第 \(i\) 行是个 \(0\) 至 \(m-1\) 的数列然后 \([j,m]\) 区间加一。而把第 \(i-1\) 行全部左移一位相当于把 \(i-1\) 行全部加上 \(1\) 再把位置 \(j'-1\) 上的元素加一。左移一位后，限制就变成了 \(a_{i,k}<a_{i-1,k}\)。左移之后的第 \(i-1\) 行相当于数列 \(1\) 至 \(m\) 再 \([j'-1,m]\) 区间加一。作差，只要有 \(k\) 使得 \(a_{i,k}-a_{i-1,k}\ge 0\) 限制就满足，否则就不满足。作差后就是一个全是 \(-1\) 的数列 \([j,m]\) 区间加一再 \([j'-1,m]\) 区间减一。显然，这样就要求加的区间比减的区间多出一段。所以当且仅当 \(j<j'-1\) 时限制才不满足，也就是说 \(j'\le j+1\) 是限制满足的充分必要条件。

所以，\(f_{i,j}\) 可以从 \(f_{i,j'}(0\le j'\le j+1)\) 转移过来。即得状态转移方程 \(f_{i,j}=\sum_{k=0}^{j+1}f_{i-1,k}\)，边界条件是 \(f_{1,k}=1(0\le k\le m)\)，答案是 \(\sum_{i=0}^mf_{n,i}\)。容易发现这个转移方程就是在对上一行做前缀和。所以我们就可以像前缀和一样转移：\(f_{i,j}=[j\ge 0]\times f_{i,j-1}+[j\le m-1\land i>1]\times f_{i-1,j+1}\)（没错，\(j\) 可以取到 \(-1\)。如果不能取到，\(f_{i-1,0}\) 就不会被计算了），边界条件是 \(f_{1,0}=1\)，答案是 \(\sum_{i=0}^mf_{n,i}=f_{n+1,m-1}\)。容易看出来这是一个有限制的走路方案数计数。因为限制关于 \(j\) 的更多,所以我们把 \(j\) 作为 \(x\) 轴方便讨论。

于是我们得到这样一个结论：答案就是从 \((0,1)\) 出发走到 \((m-1,n+1)\) 的方案数，每次可以往右走或者往左上走，且走得过程不能越过或触碰三条直线：\(x=-2,x=m+1,y=0\)。但我们知道它不能往下走，所以 \(y=0\) 不需要考虑。如下图（\(n=4,m=3\)）：

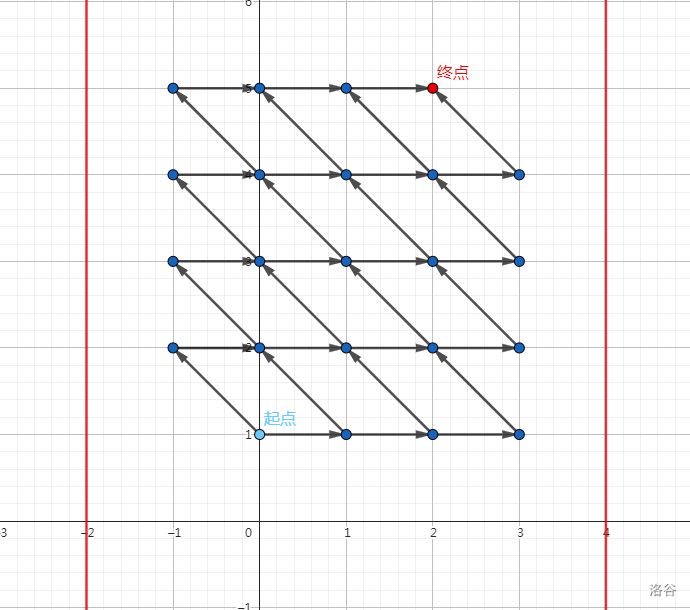
这里有很多悬浮在空中的平行四边形，还有很多坐标是负数的点，十分讨厌。我们将整个图像向下平移一格，再向右平移一格（起点变为 \((1,0)\)，终点变为 \((m,n)\)，两条直线变为 \(x=-1,x=m+2\)）：

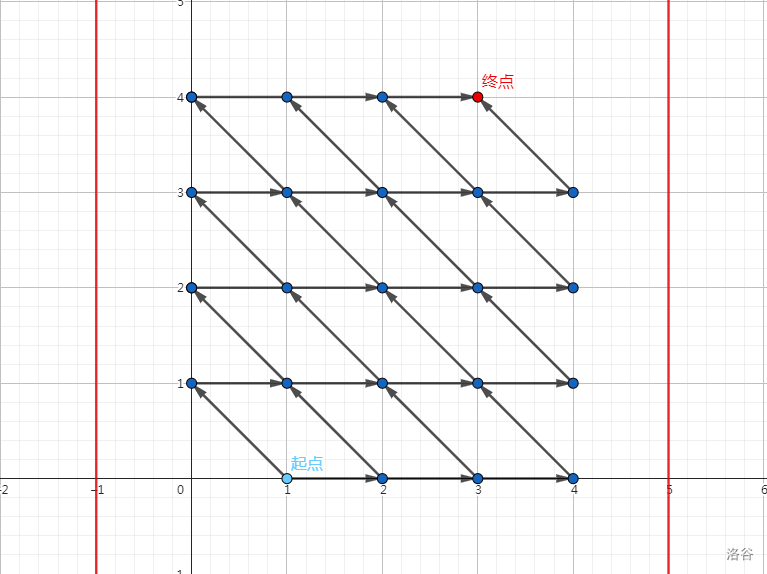
然而，直到现在我们还不会走平行四边形的计数。没有限制的情况还简单：总共往上走了 \(n\) 格，也就总共往左走了 \(n\) 格，所以往右就要总共走 \(n+m-1\) 步。所以总共走了 \(2n+m-1\) 步，其中 \(n\) 步往左上走。答案即为 \({2n+m-1}\choose{n}\)。但有限制的就很难办了。可能有人还想像 P1641 那样搞，但我们发现对称过去了之后向右的变成向左的，向左上的变成了向右上的。所以那样对称的话就会有两个阶段，两个阶段走路的规则不同，非常不可爱。

我们考虑将其转换为像 P1641 一样的向上走和向右走，约束线与 \(x\) 轴夹角为 \(\frac{\pi}{4}\)。这个是一个非常常见的技巧，对坐标系做个变换即可。具体的，将原来坐标系中的 \(y\) 轴旋转 \(\frac{\pi}{4}\)，再伸长到原来的 \(\sqrt 2\) 倍。图像就变成了下图：

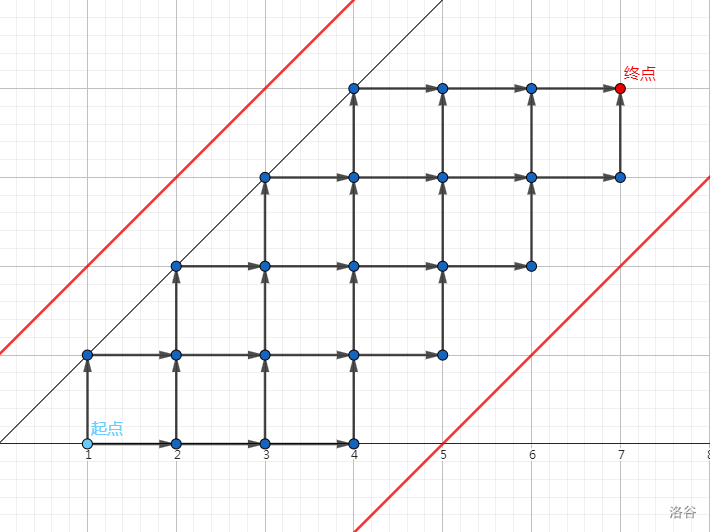
起点还在 \((1,0)\)，终点变成了 \((m+n,n)\)，两条直线变成了 \(y=x+1\) 和 \(y=x-m-2\)。

然后就可以做容斥了，用无限制路径数减去穿过 \(y=x+1\) 或 \(y=x-m-2\) 的路径数。但我们发现穿过 \(y=x+1\) 或 \(y=x-m-2\) 的路径总数并不是很好求，因为一个路径可能会多次穿过 \(y=x+1\) 的同时多次穿过 \(y=x-m-2\)。怎么处理呢？我们可以考虑它第一个穿过的是 \(y=x+1\) 还是 \(y=x-m-2\)，这两个集合显然是无交的。所以如果我们能分别求出这两个集合的大小，那么两个集合的大小之和就是穿过 \(y=x+1\) 或 \(y=x-m-2\) 的路径数量。

我们先考虑如何求出第一次穿过的是 \(y=x+1\) 的方案数。我们记穿过一次 \(y=x+1\) 为 \(A\)，穿过一次 \(y=x-m-2\) 为 \(B\)。我们现在有方法求出 \(\cdots A\cdots\) 的路径条数。怎么在此基础上求出所有 \(A\cdots\) 的路径呢？显然，我们应该把还有 \(B\) 在它前面的路径也就是 \(\cdots B\cdots A\cdots\) 的路径删去。但这么做是错的，因为 \(B\) 前面可能还有 \(A\)，于是我们再把形如 \(\cdots A\cdots B\cdots A\cdots\) 的路径加上，然后再把 \(\cdots B\cdots A\cdots B\cdots A\cdots\) 的路径减去………以此类推，直到这样的路径不存在为止。

那么怎么求呢？之前我们是把第一次接触到直线之前的对称。现在为了求出来的不重不漏，我们应该把最后一次接触到直线之后的对称，因为我们是从后往前加的。具体怎么对称呢？我们来试着玩一下：

第一次，我们把终点沿 \(y=x+1\) 轴对称过去，这样从起点到新终点的路径数就是 \(\cdots A\cdots\) 的方案数：

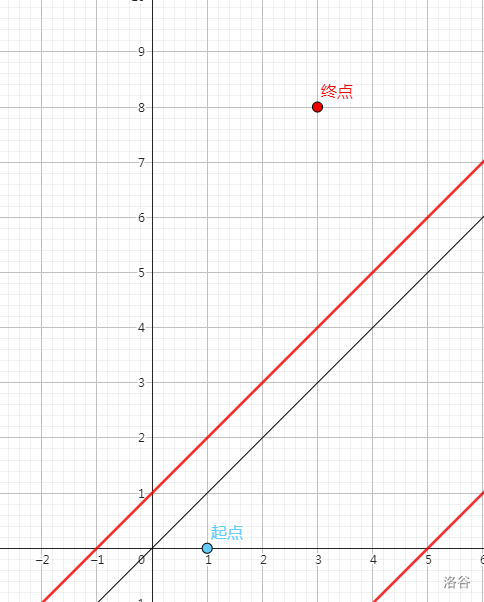
我们发现从起点到新终点之间的路径有个重要的性质：如果它会穿过一次 \(y=x-m-2\)，那么它在这之后一定会穿过至少一次 \(y=x+1\)（虽然在我给出的例子里不可能穿过 \(y=x-m-2\)），因为 \(y=x+1\) 在 \(y=x-m-2\) 上面，而新终点又在 \(y=x+1\) 上面。而这正是我们想要的性质：可以求出 \(\cdots B\cdots A\cdots\) 的方案数。我们只需要再对新终点沿 \(y=x-m-2\) 做一次反射，就可以求出 \(\cdots B\cdots A\cdots\) 的数量了。接着我们发现它仍然具有这个良好的性质：即如果从起点到新新终点的路径穿过 \(y=x+1\)，那这次穿过一定在一次穿过 \(y=x-m-2\) 之前。事实上，无论我们轴反射多少次，这条性质始终成立。对于 \(y=x+1\)，我们做轴对称的原点一定在 \(y=x+1\) 下方，所以新点就在 \(y=x+1\) 上方，所以接触了 \(y=x-m-2\) 的路径一定要在接触后再穿过一次 \(y=x+1\) 才有可能走到新点；对于 \(y=x-m-2\) 同理。而轴反射的原点一定在 \(y=x-m-2\) 上方或 \(y=x+1\) 下方可以用归纳法轻松证明。于是我们轮流对称多次就可以求出形如我们需要的方案数了。

什么时候结束对称呢？之前已经说过，直到这样的路径不存在为止。什么时候这种路径不存在？当然是终点已经不能被起点走到的时候。什么时候终点不能被起点走到？当然是终点在起点左边或起点下面时。

现在我们已经会了怎么求出第一次是 \(A\) 的路径，第一次是 \(B\) 的路径把 \(A\) 和 \(B\) 交换一下做类似方法就行了。

相信各位读者可以自行推出点 \((x,y)\) 沿直线 \(y=x+b\) 对称后的结果是什么，在此直接给出结论：结果是 \((y-b,x+b)\)。

这么做的时间复杂度是多少？我们先沿 \(y=x+1\) 做一次对称，终点变成了 \((n-1,m+n+1)\)。然后再做 \(k\) 次“先沿 \(y=x-m-2\) 对称，再沿 \(y=x+1\) 对称”，得到的就是 \((n-1-(m+3)k,m+n+1+(m+3)k)\)。而在 \(\lceil\frac{n-1}{m+3}\rceil\) 次对称操作后横坐标就一定小于 \(1\) 了，在起点左边，所以这个的时间复杂度是 \(\Theta(\frac{n}{m})\) 的。同理可证求第一次是 \(B\) 的时间复杂度也为 \(\Theta(\frac{n}{m})\)，总时间复杂度就是 \(\Theta(\frac{n}{m})\)。不过考虑到我们要预处理阶乘和快速幂算乘法逆元来做组合数，所以真正的时间复杂度应该是 \(\Theta(\frac{n\log n}{m}+n)\)。

代码

/*********************************************************************
    程序名:
    版权:
    作者: TM_Sharweek
    日期: 2025-02-22 20:42
    说明: 省选前还在做这种题的也是神人了
*********************************************************************/
#include <bits/stdc++.h>

#define p_b push_back
#define m_p make_pair
#define sec second
#define fst first
#define p_q priority_queue
#define u_m unordered_map

using namespace std;

using ll = long long;
using ull = unsigned long long;
using i128 = __int128;

const int N = 1e7 + 50;
const ll P = 1e9 + 7;
const ll LTYL = 10071204121099;

ll jc[N];// 朴实无华的拼音

ll qpow(ll a, ll x) {
	ll ans = 1;
	while (x) {
		if (x % 2)
			ans = ans * a % P;
		a = a * a % P;
		x >>= 1;
	}
	return ans;
}

ll C(ll n, ll m) {
	return n > m || n < 0 ? 0 : jc[m] * qpow(jc[n], P - 2) % P * qpow(jc[m - n], P - 2) % P;
}

void dc(ll &a, ll &b, ll jj) {
	swap(a, b);
	a -= jj, b += jj;
}// 把 (a,b) 沿 y=x+jj 做轴反射

int main() {
//	freopen("LuoTianyi.in","r",stdin);
//	freopen("YuezhengLing.out","w",stdout);
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	ll n, m;
	cin >> n >> m;
	ll edx = n + m, edy = n;
	ll jj1 = 1, jj2 = -m - 2;
	ll qwq = 0;
	jc[0] = 1;
	for (int i = 1; i <= int(1e7); i++) {
		jc[i] = jc[i - 1] * i % P;
	}
	while (1 <= edx && 0 <= edy) {
		dc(edx, edy, jj1);
		qwq = (qwq + C(edx - 1, edx + edy - 1)) % P;// 从 (1,0) 走到 (edx,edy) 的方案数
		if (1 > edx || 0 > edy)// 边界处理
			break;
		dc(edx, edy, jj2);
		qwq = (qwq + P - C(edx - 1, edx + edy - 1)) % P;
	}
	edx = n + m, edy = n;
	while (1 <= edx && 0 <= edy) {
		dc(edx, edy, jj2);
		qwq = (qwq + C(edx - 1, edx + edy - 1)) % P;
		if (1 > edx || 0 > edy)
			break;
		dc(edx, edy, jj1);
		qwq = (qwq + P - C(edx - 1, edx + edy - 1)) % P;
	}
	cout << (C(n, 2 * n + m - 1) + P - qwq) % P << endl;

	return -1;// 炸死你
}

总而言之，就是用轴反射来做有限制的路径计数问题，同时通过考虑组合意义来把 DP 变成有限制的路径计数问题。