【OI学习笔记】AC自动机

前言

蒟蒻的第一篇学习笔记，就献给我学了两三遍的AC自动机吧！蒟蒻希望大家能够通过我的思考对AC自动机获得初步的理解！

另外，本篇文章将围绕P5357 【模板】AC 自动机这道题来讲解，这道题是二次加强版，所以我们需要写优化。

前置知识

AC自动机主要由字典树（Trie）以及KMP的思想组成的。重点就是它是由 KMP 的思想来处理的，所以我没有学懂 KMP 但是学“懂”了 AC自动机……

综上，前置知识有以下几点：

• 字典树（Trie）
• BFS
• 拓扑排序（优化）

AC自动机

题面分析

题目中给出了主串 \(S\) 以及 \(n\) 个模式串 \(T\)，问我们这 \(n\) 个模式串 \(T\) 分别在主串 \(S\) 中出现了几次。

KMP思想的应用

在学习 KMP 后，我们知道 KMP 算法可以在 \(O(n)\) 的时间复杂度下完成对一个模式串的匹配，其核心就是 next 数组（最长公共前后缀）的应用，使得在字符串失配时可以快速找到模式串的合适位置继续匹配。

那么在多个模式串的匹配时，我们也可以迁移这种思想——一些模式串可能有公共的部分，当一个模式串失配时，它的后缀可能是其他模式串的前缀，此时我们跳转到符合条件的模式串即可继续匹配。

说起来真的很抽象呢，让我们来代入一组数据解释以上的结论：

主串 \(S=abaaa\)

模式串 \(T_1=ab,T_2=aa\)

很显然，模式串 \(T_2\) 的一个后缀“a”是 \(T_2\) 的一个前缀，所以当匹配模式串 \(T_2\) 失配时，可以跳转到 \(T_1\) 的第二个字符“b”继续匹配。

以上便是KMP思想在AC自动机上的运用，通过 KMP 的思想，我们处理出 fail（失配指针），以便在失配后可以快速跳转到下一个匹配对象。

Trie的应用

接下来让我们想一想，公共前后缀、跳转……似乎可以使用一个数据结构来完成这些操作，没错，就是字典树（Trie），我们使用字典树把模式串存储下来，便可以更方便地实现 fail 指针的功能。

下面放出一些字典树部分的代码来配合理解：

这里笔者存储字典树的方式是数组 trie[maxn][26]（无结构体），endpos[] 来记录模式串的末尾位置，fail[i] 是字典树节点 \(i\) 的 fail 指针（在这里还没有处理到），tot 是字典树的节点总数。

//Trie部分
ll trie[maxn][26],fail[maxn],tot,n,endpos[maxn];
void insert(string s,ll index){//参数有模式串s和其序号index
	ll i,p = 0;//p变量来存储当前的trie节点
	for(i = 0;i < s.size();i++){
		if(!trie[p][s[i] - 'a'])//如果不存在这个节点，就创建一个
			trie[p][s[i] - 'a'] = ++tot;
		p = trie[p][s[i] - 'a'];//跳转
	}
	endpos[index] = p;//记录末尾节点
	return;
}

接下来还是这一组数据，我们再引入一个模式串 \(T_3=a\)，按照上述程序建立的字典树应如图：

主串 \(S = abaaa\)

模式串 \(T_1=ab,T_2=aa,T_3=a\)

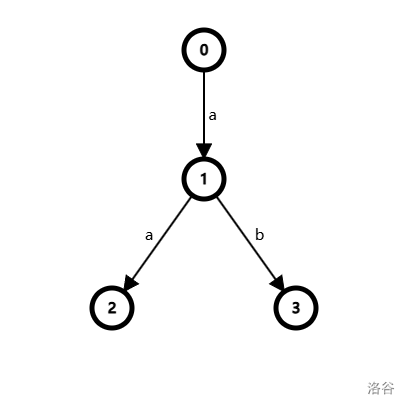
此时 endpos[1]=3,endpos[2]=2,endpos[3]=1。

fail 失配指针的计算

我们以上述数据的模式串 \(T_1\) 和 \(T_2\) 来考虑，同之前所说，当匹配到 \(T_2=aa\) 的第二个字符“a”失配时，由于“a”是“ab”的前缀，所以可以跳转到“ab”中的字符“a”的位置继续匹配，即 fail[2]=1。

从这个例子中，我们大概可以发现一些规律，fail 指针指向的位置，其实就是位于当前字典树节点时所形成的字符串的最长真后缀。

比如这个例子中，fail[2] 指向的就是字符串“aa”的最长真后缀“a”的位置。

这里需要特别注意，是最长真后缀！

那么这个 fail 指针究竟应该如何去计算呢？

我们再次借助这个例子来探究：

节点 \(p=1\) 时，字符串为“a”。

节点 \(p=2\) 位置的字符串“aa”=“a”+“a”。

这里前者的“a”为节点 \(p=1\) 的字符串，后者的“a”是节点 \(p=1\) 和节点 \(p=2\) 之间的边。

我们需要求的 fail[2]，也就是节点 \(p=2\) 位置的字符串“aa”的最长真后缀的位置。

节点 \(p=2\) 的字符串“aa”的最长真后缀“a”其实就等于它的父节点的最长真后缀加上它们之间的边，即“”+“a”=“a”。

好的，接下来形式化地来总结以上的结论。

有节点 \(u\) 及其对应的字符串 \(S_u\)，和 \(u\) 的子节点 \(v\) 及其对应的字符串 \(S_v\)，\(u\) 和 \(v\) 之间的边代表字符 \(S_i\)，

\(S_v 的最长真后缀 = S_u 的最长真后缀 + S_i\)

所以 \(fail[v]=trie[fail[u]][S_i - 'a']\)。

在这个公式中，\(fail[u]\) 是节点 \(u\) 的最长真后缀的位置，\(trie[fail[u]][S_i - 'a']\) 表示把 \(u\) 节点字符串的最长真后缀加上字符 \(S_i\)。

至此，fail 指针终于得到了计算。

fail 指针计算时的路径压缩

注意到我们更新 fail 指针需要从父节点向子节点更新，那么在遍历子节点时，有如下代码：

for(i = 0;i < 26;i++){
	if(trie[u][i]){
		……
	}
}

那么如果父节点 \(u\) 没有子节点 \(i\) 的话，我们该如何处理？如果直接跳过，会导致后续匹配过程中出现大量无效的回溯，那太慢了！

解决办法就是——路径压缩，即让不存在的子节点指向 trie[fail[u]][i]，来减少匹配操作的步数，如下代码：

trie[u][i] = trie[fail[u]][i];

这样处理后，在匹配过程中遇到缺失的边时，可以直接跳转到其 fail 指针对应节点的相应字符位置。

路径压缩使AC自动机获得了类似 KMP 的"一步跳转"能力：

• 当字符匹配失败时，无需沿着 fail 链回溯；
• 可以直接通过压缩后的边跳转到下一个可能匹配的位置。

BFS

万事俱备，可以开始更新 fail 指针了！

我们知道 fail 指针需要从父节点向子节点更新，而且字典树深处的节点的 fail 指针可能需要较浅位置的节点，所以我们使用BFS进行遍历。

终于可以放代码啦！！！

//fail指针
void BFS(){
	ll i,u,v;//u表示当前节点，v表示子节点
	queue<ll> Q;//建立队列
	for(i = 0;i < 26;i++){//遍历根节点0的子节点
		if(trie[0][i]){
			fail[trie[0][i]] = 0;//根节点的子节点的fail指针指向根节点
			Q.push(trie[0][i]);//加入队列
		}
	}
	while(!Q.empty()){//BFS
		u = Q.front();//提取队首
		Q.pop();//记得pop!!!
		for(i = 0;i < 26;i++){
			v = trie[u][i];
			if(v){
				//存在该子节点，更新fail指针
				fail[v] = trie[fail[u]][i];
				Q.push(v);//加入队列
			}else{
				//不存在该子节点，路径压缩
				trie[u][i] = trie[fail[u]][i];
			}
		}
	}
	return;
}

匹配

接下来我们就可以开始匹配主串了！

先放代码再解释：

ll tag[maxn];
void AC(){
	ll i,p = 0,j;
	for(i = 0;i < S.size();i++){
		p = trie[p][S[i] - 'a'];//跳转到字典树中该字符所在的位置
		tag[p]++;//增加标记
	}
	return;
}

代码中 S 为主串，tag[i] 用于存储字典树中节点 \(i\) 被标记的次数，其实也就是以节点 \(i\) 处为末尾的字符串的出现次数。

这么看似乎我们就可以遍历输出模式串末尾位置（\(endpos[i]\)）的 \(tag[]\) 标记来解决这个算法了。

NONONONONO!!!!

快点使用你超强的注意力，注意到：

例如对于模式串“a”和“aba”，当成功匹配“aba”时，“aba”末尾的“a”其实也应该被计入“a”的标记中啊！

但是由于字典树的结构，如图：

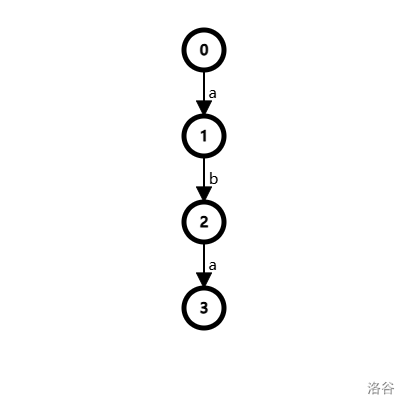
当“aba”匹配成功时，\(tag[1]=1,tag[2]=1,tag[3]=1\)。

但是“aba”中明明有两个“a”！应该有 \(tag[1]=2\)！

所以我们应该将 \(tag[3]\) 的值也累计在 \(tag[1]\) 上。

OK，回顾刚才的思考过程。

由于“a”是“aba”的后缀，所以我们要将“aba”的计数累加在“a”上。

似乎很熟悉呢，我记得 fail 指针记录的位置就是最长真后缀的位置呢。

也就是说，对于节点 \(i\)，应有 \(tag[fail[i]]+=tag[i]\)。

现在就可以暴力计算了，这个问题终于算是解决了！

完结撒花！

拓扑排序优化

很明显，这是一道二次加强的题，普通的暴力计算肯定无法满足它的数据，我们考虑进行优化。

如何进行优化呢？

回顾刚才的公式，对于节点 \(i\)，应有 \(tag[fail[i]]+=tag[i]\)。

根据前面的介绍，我们可以很容易想到一个节点很可能是多个节点的 fail 指针，也就是说，fail 指针会形成一个有向图的结构（如下图）：

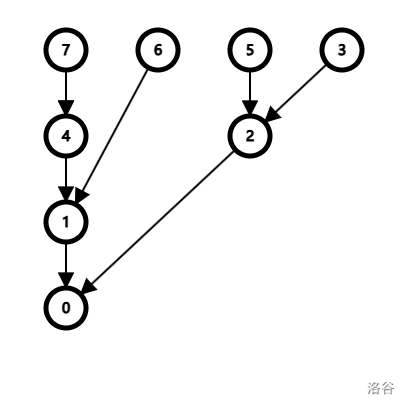
这不就是拓扑排序吗！

所以我们使用拓扑排序的方法，以 fail 指针建边，记录每个节点的入度，然后进行拓扑排序累加，最后再输出。

这下真的完结撒花啦！！！

完整代码

#include <iostream>
#include <string>
#include <queue>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long ll;
const ll maxn = 2000200;

string S;//主串

//trie部分
ll trie[maxn][26],fail[maxn],tot,n,endpos[maxn];
void insert(string s,ll index){
	ll i,p = 0;
	for(i = 0;i < s.size();i++){
		if(!trie[p][s[i] - 'a'])
			trie[p][s[i] - 'a'] = ++tot;
		p = trie[p][s[i] - 'a'];
	}
	endpos[index] = p;
	return;
}

//fail指针
void BFS(){
	ll i,u,v;
	queue<ll> Q;
	for(i = 0;i < 26;i++){
		if(trie[0][i]){
			fail[trie[0][i]] = 0;
			Q.push(trie[0][i]);
		}
	}
	while(!Q.empty()){
		u = Q.front();
		Q.pop();
		for(i = 0;i < 26;i++){
			v = trie[u][i];
			if(v){
				fail[v] = trie[fail[u]][i];
				Q.push(v);
			}else{
				trie[u][i] = trie[fail[u]][i];
			}
		}
	}
	return;
}

//自动机匹配
ll tag[maxn];
void AC(){
	ll i,p = 0,j;
	for(i = 0;i < S.size();i++){
		p = trie[p][S[i] - 'a'];
		tag[p]++;
	}
	return;
}

//拓扑排序部分
vector<ll> V[maxn];
ll indeg[maxn];

int main(){
	ll i;
	string op;//模式串
	
	cin>>n;
	for(i = 1;i <= n;i++){
		cin>>op;
		insert(op,i);
	}
	BFS();
	for(i = 1;i <= tot;i++){
		V[i].push_back(fail[i]);//建立fail指针树
		indeg[fail[i]]++;//记录入度
	}
	
	cin>>S;
	AC();

	queue<ll> Q;//拓扑排序队列
	ll u,v;
	for(i = 0;i <= tot;i++){
		if(indeg[i] == 0){
			Q.push(i);//入队
		}
	}
	while(!Q.empty()){
		u = Q.front();
		Q.pop();
		for(i = 0;i < V[u].size();i++){
			v = V[u][i];
			tag[v] += tag[u];//累加
			indeg[v]--;
			if(indeg[v] == 0) Q.push(v);//入队
		}
	}
	
	for(i = 1;i <= n;i++) cout<<tag[endpos[i]]<<endl;//输出
	return 0;//完结撒花！！
}

后记

感谢大家的阅读！希望大家能通过我的文章获得一些初步理解，有任何错误请大家帮忙指出，万分感谢！！！