学习笔记——二叉树相关算法的实现(Java语言版)
二叉树遍历概念和算法
遍历(Traverse):
所谓遍历(Traversal)是指沿着某条搜索路线,依次对树中每个结点均做一次且仅做一次访问。
从二叉树的递归定义可知,一棵非空的二叉树由根结点及左、右子树这三个基本部分组成。
因此,在任一给定结点上,可以按某种次序执行三个操作:
⑴ 访问结点本身(D),
⑵ 遍历该结点的左子树(L),
⑶ 遍历该结点的右子树(R)。
先序/根遍历DLR:根 左子树 右子树
中序/根遍历LDR:左子树 根 右子树
后根/序遍历LRD:左子树 右子树 根
中序/根遍历LDR:左子树 根 右子树
后根/序遍历LRD:左子树 右子树 根
注意:由于树的递归定义,其实对三种遍历的概念其实也是一个递归的描述过程
算法实现:
二叉树结点类
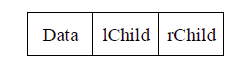
/** * 二叉链表的结点 * @author shangyang * */ public class Node { Object value; // 结点值 Node leftChild; // 左子树的引用 Node rightChild; // 右子树的引用 public Node(Object value) { super(); this.value = value; } public Node(Object value, Node leftChild, Node rightChild) { super(); this.value = value; this.leftChild = leftChild; this.rightChild = rightChild; } @Override public String toString() { return "Node [value=" + value + ", leftChild=" + leftChild + ", rightChild=" + rightChild + "]"; } }
二叉树方法接口类

/** * 二叉树的接口 * 可以有不同的实现类,每个类可以使用不同的存储结构,比如顺序结构、链式结构 * @author shangyang * */ public interface BinaryTree { /** * 是否为空树 */ public boolean isEmpty(); /** * 树结点数量 */ public int size(); /** * 获取树的高度 */ public int getHeight(); /** * 查询指定值的结点 * @param value * @return */ public Node findKey(Object value); /** * 前序递归遍历 */ public void preOrderTraverse(); /** * 中序递归遍历 */ public void inOrderTraverse(); /** * 后序递归遍历 */ public void postOrderTraverse(); /** * 按照层次遍历(借助队列) */ public void levelOrderByStack(); /** * 中序非递归遍历 */ public void inOrderByStack(); }
实现二叉树接口类
创建树的根对象,并写出构造函数。
public class LinkedBinaryTree implements BinaryTree { private Node root; // 根结点 public LinkedBinaryTree() { } public LinkedBinaryTree(Node root) { this.root = root; }
}
创建二叉树

// 创建一个二叉树 Node nodeF = new Node("F",null,null); Node nodeE = new Node("E",null,null); Node nodeD = new Node("D",null,null); Node nodeC = new Node("C",nodeF,null); Node nodeB = new Node("B",nodeD,nodeE); Node nodeA = new Node("A",nodeB,nodeC); // 声明nodeA为根结点 BinaryTree btree = new LinkedBinaryTree(nodeA);
判断二叉树是否为空
为空返回true,不为空返回false
public boolean isEmpty() { return root == null; }
输出二叉树结点数量
运用递归的思想,二叉树结点树 = 左子树结点数量 + 右子树结点数量 + 1
public int size() { System.out.println("二叉树结点数量: "); return this.size(root); } private int size(Node root) { if(root == null) { return 0; } else { // 获取左子树的数量 int nl = this.size(root.leftChild); // 获取右子树的数量 int nr = this.size(root.rightChild); // 返回左子树、右子树size之和并加1 return nl + nr + 1; } }
二叉树的深度(高度)
如果二叉树为空,则其深度为0。
如果二叉树只有根结点,无左右子树,则其深度为1。
如果二叉树结点数大于1,则用递归的思想计算其深度。二叉树的深度 = 左右子树的最大深度 + 1。
public int getHeight() { System.out.println("二叉树的高度是 :"); return this.getHeight(root); } private int getHeight(Node root) { if(root == null) { return 0; } else { // 获取左子树的高度 int nl = this.getHeight(root.leftChild); // 获取右子树的高度 int nr = this.getHeight(root.rightChild); // 返回左子树、右子树较大高度并加1 return nl > nr ? nl + 1 : nr + 1; } }
在二叉树中查找某个值
运用递归的思想,将要查找的值逐个与根结点,根结点的左子树和右子树的值进行比较,并进行返回。
public Node findKey(Object value) { return this.findKey(value,root); } private Node findKey(Object value,Node root) { // 结点为空,可能是整个树的根结点,也可能是递归调用中叶子结点中左孩子和右孩子 if(root == null) { return null; } else if (root != null && root.value == value) { return root; } else { // 递归体 Node leftnode = this.findKey(value,root.leftChild); Node rightnode = this.findKey(value, root.rightChild); if(leftnode != null && leftnode.value == value) { return leftnode; } else if (rightnode != null && rightnode.value == value) { return rightnode; } else { return null; } } }
先序递归遍历
若二叉树非空,则依次执行如下操作:
⑴ 访问根结点;
⑵ 遍历左子树;
⑶ 遍历右子树。
public void preOrderTraverse() { // 输出根结点的值 if(root != null) { System.out.print(root.value + " "); // 对左子树进行先序遍历 // 构建一个二叉树,根是左子树的根 BinaryTree leftTree = new LinkedBinaryTree(root.leftChild); leftTree.preOrderTraverse(); // 对右子树进行先序遍历 // 构建一个二叉树,根是左子树的根 BinaryTree rightTree = new LinkedBinaryTree(root.rightChild); rightTree.preOrderTraverse(); } }
中序递归遍历
若二叉树非空,则依次执行如下操作:
⑴ 遍历左子树;
⑵ 访问根结点;
⑶ 遍历右子树。
public void inOrderTraverse() { System.out.println("中序遍历"); this.inOrderTraverse(root); System.out.println(); } private void inOrderTraverse(Node root) { if(root != null) { // 遍历左子树 this.inOrderTraverse(root.leftChild); // 输出根的值 System.out.print(root.value + " "); // 遍历右子树 this.inOrderTraverse(root.rightChild); } }
后续递归遍历
若二叉树非空,则依次执行如下操作:
⑴ 遍历左子树;
⑵ 遍历右子树;
⑶ 访问根结点。
public void postOrderTraverse() { System.out.println("后序遍历"); this.postOrderTraverse(root); System.out.println(); } private void postOrderTraverse(Node root) { if(root != null) { // 遍历左子树 this.postOrderTraverse(root.leftChild); // 遍历右子树 this.postOrderTraverse(root.rightChild); // 输出根的值 System.out.print(root.value + " "); } }
按照层次遍历(借助队列)
按照从上到下、从左到右的次序进行遍历。先遍历完一层,再遍历下一层,因此又叫广度优先遍历。
该方法可以借助java中提供queue队列接口来完成。LinkedList实现了该接口。
public void levelOrderByStack() { if(root == null) return; Queue<Node> queue = new LinkedList<Node>(); queue.add(root); while(queue.size() != 0) { int len = queue.size(); for(int i = 0; i < len; i++) { Node temp = queue.poll(); System.out.print(temp.value + " "); if(temp.leftChild != null) queue.add(temp.leftChild); if(temp.rightChild != null) queue.add(temp.rightChild); } } }
中序非递归遍历(借助栈)
(1) 若根结点不为空,则将其放如栈中,并判断其左子树是否为空。
(2) 若不为空,则将子树根结点放入栈中,并继续向下判断,直至左子树为空。
(3) 若栈中有结点,则将其取出,并对其右子树根结点进行(1)(2)步骤,直至无结点或栈中元素为空。
public void inOrderByStack() { // 创建栈 Deque<Node> stack = new LinkedList<Node>(); Node current = root; while(current != null || !stack.isEmpty()) { while(current != null) { stack.push(current); current = current.leftChild; } if(!stack.isEmpty()) { current = stack.pop(); System.out.print(current.value + " "); current = current.rightChild; } } }
作者:殇央 © 转载请注明出处。
-------------------------------------------
如果有错误或者更优化的解决方案,欢迎大家在评论区留言探讨。
也可以给我的个人公众号私信留言。
如果觉得这篇文章对你有小小的帮助的话,记得在右下角点个“推荐”哦,博主在此感谢!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号