CRC 详解

http://www.barrgroup.com/Embedded-Systems/How-To/Additive-Checksums

CRC Series, Part 1: Additive Checksums

Sat, 2007-12-01 23:21 - webmaster

by Michael Barr

Whenever you connect two or more computers together with the intent of exchanging information,

you assume that the exchange will take place without errors.

But what if some of the data is lost or corrupted in transit?

Communication protocols usually attempt to detect such errors automatically.

To do that they use checksums.

The most important part of listening to someone speak is ensuring that you've heard them correctly.

Your brain performs the tasks of error detection and correction for you, automatically.

It does this by examining extra bits of information from the speaker and the speech;

if a phrase or sentence makes sense as a whole and it makes sense coming from the mouth of the particular speaker,

then the individual words were probably heard correctly.

The same principle applies when you are reading.

But what happens when computers are communicating with one another?

How does the receiving computer know if an error has occurred in transmission?

Establishing correctness is more difficult for computers than humans.

At the lowest level, communication between computers consists of nothing but a stream of binary digits.

Meaning is only assigned to that particular sequence of bits at higher levels.

We call that meaningful sequence of bits the message; it is analogous to a spoken or written phrase.

If one or more bits within the message are inverted (a logic one becomes a logic zero, or vice versa)

as it travels between computers, the receiver has no way to detect the error.

No environmental or syntactical context is available to the receiver,

since it cannot understand the message in its transmitted form.

Parity Bits

If we want communicating computers to detect and correct transmission errors automatically,

we must provide a replacement for context. This usually takes the form of an error correction code or error detection code.

A simple type of error detection code that you are probably already familiar with is called a parity bit.

A parity bit is a single, extra binary digit that is appended to the message by the sender and transmitted along with it.

Depending on the type of parity used, the parity bit ensures that the total number of logic ones sent is

even (even parity) or odd (odd parity).

For an example of even parity, consider the sequence:

10101110 1

in which the eight-bit message contains five ones and three zeros.

The parity bit is one in this case to force the total number of ones in the transmitted data stream to be even.

When a parity bit is appended to a message, one additional bit of data must be sent between the computers.

So there must be some benefit associated with the lost bandwidth.

The most obvious benefit is that if any single bit in the message is inverted during transmission,

the number of ones will either increase or decrease by one, thus making the received number of ones odd and the parity incorrect.

The receiver can now detect such an error automatically and request a retransmission of the entire stream of bits.

Interestingly, the receiver can also now detect any odd number of bit inversions.

(Note that all of this still applies even when the parity bit is one of the inverted bits.)

However, as you may have already noticed, if two bits are inverted (two ones become zeros, for example),

the parity of the stream of bits will not change;

a receiver will not be able to detect such errors.

In fact, the same is true for any even number of bit inversions.

A parity bit is a weak form of error detection code.

It has a small cost (one bit per message), but it is unable to detect many types of possible errors.

(By the way, odd parity has the same costs, benefits, and weaknesses as even parity.)

Perhaps this is not acceptable for your application.

An alternative that might occur to you is to send the entire message twice.

If you're already spending bandwidth sending an error detection code, why not spend half of the bandwidth?

The problem is that you could actually be spending much more than half of the available bandwidth.

If a computer receives two copies of a message and the bits that comprise them aren't exactly the same,

it cannot tell which one of the two is correct. In fact, it may be that both copies contain errors.

So the receiver must request a retransmission whenever there is a discrepancy

between the message and the copy sent as an error detection code.

With that in mind, let's compare the bandwidth costs of using a parity bit vs. resending the entire message.

We'll assume that all messages are 1,000-bits long and that the communications channel

has a bit error rate (average number of inverted bits) of one per 10,000 bits sent.

Using a parity bit, we'd spend 0.1% of our bandwidth sending the error detection code

(one bit of error protection for 1,000 bits of message) and have to retransmit one out of every 10 messages due to errors.

If we send two complete copies of each message instead, the smallest unit of transmission is 2,000 bits

(50% of our bandwidth is now spent sending the error detection code).

In addition, we'll have to retransmit one out of every five messages.

Therefore, the achievable bandwidths are approximately 90% and 40%, respectively.

As the width of the code increases, the message plus code lengthens and becomes more vulnerable to bit errors and,

as a result, expensive retransmissions.

From this type of analysis it should be clear that keeping the size of an error detection code as small as possible is a good thing,

even if it does mean that some types of errors will be undetectable.

(Note that even sending two copies of the message is not a perfect solution.

If the same bit errors should happen to occur in both copies, the errors will not be detected by the receiver.)

In addition to reducing the bandwidth cost of transmitting the error detection code itself,

this also increases the message throughput.

But we still don't want to go so far as using a one-bit error detection scheme like parity.

That would let too many possible errors escape detection.

In practice, of course, we can achieve far better error detection capabilities than just odd numbers of inverted bits.

But in order to do so we have to use error detection codes that are more complex than simple parity, and also contain more bits.

I'll spend the remainder of this column and most of the next two discussing the strengths and weaknesses of various types of checksums,

showing you how to compute them, and explaining how each can be best employed for purposes of error detection.

Checksums

As the name implies, a checksum usually involves a summation of one sort or another.

For example, one of the most common checksum algorithms involves treating the message like a sequence of bytes and summing them.

Listing 1 shows how this simple algorithm might be implemented in C.

uint8_t Sum( uint8_t const message[ ], int nBytes )
{
  uint8_t sum = 0;
  
  while ( nBytes-- > 0 )
  {
    sum += *( message++ );
  }
  
  return ( sum );
  
} /* Sum() */

Listing 1. A sum-of-bytes checksum

The sum-of-bytes algorithm is straightforward to compute.

However, understanding its strengths and weaknesses as a checksum is more difficult.

What types of errors does it detect? What errors is it unable to detect?

These are important factors to consider whenever you are selecting a checksum algorithm for a particular application.

You want the algorithm you choose to be well matched to the types of errors you expect to occur in your transmission environment.

For example, a parity bit would be a poor choice for a checksum if bit errors will frequently occur in pairs.

A noteworthy weakness of the sum-of-bytes algorithm is that no error will be detected

if the entire message and data are somehow received as a string of all zeros.

(A message of all zeros is a possibility, and the sum of a large block of zeros is still zero.)

The simplest way to overcome this weakness is to add a final step to the checksum algorithm:

invert the bits of the final sum.

The new proper checksum for a message of all zeros would be FFh.

That way, if the message and checksum are both all zeros, the receiver will know that something's gone terribly wrong.

A modified version of the checksum implementation is shown in Listing 2.

uint8_t SumAndInvert( uint8_t const message[ ], int nBytes )
{
  uint8_t sum = 0;
  
  while ( nBytes-- > 0 )
  {
    sum += *( message++ );
  }
  
  return ( ~sum );
  
} /* SumAndInvert() */

Listing 2. A slightly more robust sum-of-bytes checksum algorithm

This final inversion does not affect any of the other error detection capabilities of this checksum,

so let's go back to discussing the basic sum-of-bytes algorithm in Listing 1.

First, it should be obvious that any single bit inversion in the message or checksum will be detectable.

Such an error will always affect at least one bit within the checksum.

(It could affect more, of course, but not less.)

Observe that the sum-of-bytes is performed by essentially lining up all of the bytes that comprise the message and performing addition on them, like this:

Because of this mathematical arrangement, simultaneous single-bit inversions could occur in each of any number of the "columns."

At least one bit of the checksum will always be affected.

No matter how the inversions occur, at least the lowest-order column with an error will alter the checksum.

This is an important point, because it helps us to understand the broader class of errors that can be detected by this type of checksum.

I'll say it again: no matter how the inversions occur, at least the lowest order column with an error will alter the checksum,

which means that two or more bit inversions in higher-order columns may cancel each other out.

As long as the lowest-order column with an error has only one, it doesn't matter what other errors may be hidden within the message.

Now let's step back for a minute and talk about errors more formally.

What exactly does a transmission error look like? Well, the first and most obvious type of error is a single bit that is inverted.

That happens sometimes and is easy to detect (even a parity bit will do the job).

Other times, bit inversions are part of an error burst. Not all of the bits within an error burst must be inverted.

The defining characteristic is simply an inverted bit on each end. So an error burst may be 200 bits long, but contain just two inverted bits--one at each end.

A sum-of-bytes checksum will detect the vast majority of error bursts, no matter what their length.

However, describing exactly which ones is generally difficult.

Only one class of error bursts is always detectable: those of length eight bits or less. As long as the two inverted bits

that bound the error burst have no more than six bits between them, the error will always be detected by this algorithm.

That's because our previous requirement for error detection--that the lowest-order column with an error have only one error--is always met

when the length of the error burst is no longer than the width of the checksum.

We can know with certainty that such errors will always be detected.

Of course, many longer error bursts will also be detected.

The probability of detecting a random error burst longer than eight bits is 99.6%.

Errors will only be overlooked if the modified message has exactly the same sum as the original one, for which there is a 2-8 chance.

That's much better error detection than a simple parity bit, and for not too much more cost.

The sum-of-bytes algorithm becomes even more powerful when the width of the checksum is increased.

In other words, increasing the number of bits in the checksum causes it to detect even more types of errors.

A 16-bit sum-of-words checksum will detect all single bit errors and all error bursts of length 16 bits or fewer.

It will also detect 99.998% of longer error bursts.

A 32-bit sum will detect even more errors.

In practice, this increase in performance must be weighed against the increased cost of sending the extra checksum bits as part of every exchange of data.

The Internet Checksum

Many protocol stacks include some sort of a checksum within each protocol layer.

The TCP/IP suite of protocols is no exception in this regard.

In addition to a checksum at the lowest layer (within Ethernet packets, for example), checksums also exist within each IP, UDP, and TCP header.

Figure 1 shows what some of these headers look like in the case of some data sent via UDP/IP.

Here the fields of the IP header are summed to generate the 16-bit IP checksum and the data, fields of the UDP header,

and certain fields of the IP header are summed to generate the 16-bit UDP checksum.

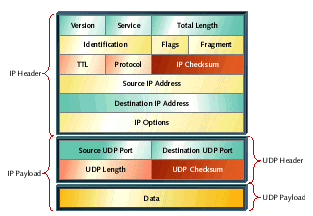
Figure 1. UDP and IP headers with checksum fields highlighted

A function that calculates the IP header checksum is shown in Listing 3.

This function can be used before sending an IP packet or immediately after receiving one.

If the packet is about to be sent, the checksum field should be set to zero before calculating the checksum and filled with the returned value afterward.

If the packet has just been received, the checksum routine is expected to return a value of 0xFFFF to indicate that the IP header was received correctly.

This result is a property of the type of addition used to compute the IP checksum.

uint16_t NetIpChecksum( uint16_t const ipHeader[ ], int nWords )
{
  uint32_t sum = 0;
  
  /*
   * IP headers always contain an even number of bytes.
   */
  while ( nWords-- > 0 )
  {
    sum += *( ipHeader++ );
  }
  
  /*
   * Use carries to compute 1's complement sum.
   */
  sum = ( sum >> 16 ) + ( sum & 0xFFFF );
  sum += sum >> 16;
  
  /*
   * Return the inverted 16-bit result.
   */
  return ( (unsigned short) ~sum );
  
} /* NetIpChecksum() */

Listing 3. IP header checksum calculation

The IP header to be checksummed should be passed to NetIpChecksum() as an array of 16-bit words.

Since the length of an IP header is always a multiple of four bytes,

it is sufficient to provide the header length as a number of 16-bit words.

The checksum is then computed by the function and returned to the caller for insertion into the header for validation of the header contents.

When you first look at this function, you may be overcome with a feeling of deja vu.

The IP checksum algorithm begins in much the same way as the sum-of-bytes algorithm I discussed earlier.

However, this algorithm is actually different. First,

of course, we're computing a 16-bit checksum instead of an eight-bit one, so we're summing words rather than bytes.

That difference is obvious. Less obvious is that we're actually computing a ones complement sum.

Recall that most computers store integers in a twos complement representation.

Simply adding two integers, as we did in the previous algorithm, will therefore result in a twos complement sum.

In order to compute the ones complement sum, we need to perform our addition with "end around carry."

This means that carries out of the most significant bit (MSB) are not discarded, as they were previously.

Instead, carries are added back into the checksum at the least significant bit (LSB).

This could be done after each addition, but testing for a carry after each addition is expensive in C.

A faster way is to let the carries accumulate in the upper half of a 32-bit accumulator.

Once the sum-of-words is complete, the upper half of the 32-bit accumulator is turned into a 16-bit value

and added to the 16-bit twos complement sum (the lower half).

One final carry is possible at that point, and must be included in the final sum.

The IP checksum is the inverted ones complement sum of all of the words in the IP header.

For checksum purposes, ones complement arithmetic has an important advantage over twos complement arithmetic.

Recall that the biggest weakness of a parity bit is that it can't detect a pair of bit errors or any even number of errors, for that matter.

A twos complement sum suffers from a similar weakness.

Only one of the bits in the sum (the MSB) is affected by changes in the most significant of the 16 columns.

If an even number of bit errors occurs within that column, the checksum will appear to be correct and the error will not be detected.

A ones complement sum does not suffer this weakness.

Because carries out of the MSB are added back into the LSB during a ones complement sum,

errors in any one column of the data will be reflected in more than one bit of the checksum.

So a ones complement sum is a stronger checksum (for example, will detect more errors) than a twos complement sum,

and only slightly more expensive. Hence, it is chosen for use in a lot of different situations.

The checksums within the UDP and TCP headers are computed in exactly the same way as the IP checksum.

In fact, the only major difference is the set of words over which the sum is calculated.

(A minor difference is that UDP checksums are optional.)

In both cases, these layer 4 protocols include the message, their own header fields, and a few important fields of the IP header in the checksum calculation.

The inclusion of some IP header fields in the UDP and TCP checksums is one of the biggest reasons

that these layers of the protocol stack cannot be completely separated from the IP layer in a software implementation.

The reason that IP checksums include only the IP header is that many intermediate computers must

validate, read, and modify the contents of the IP header as a packet travels from its source to the destination.

By reducing the number of words involved in the calculation, the speed with which all IP packets move across the Internet is improved.

Including a larger set of words in the UDP and TCP checksums does not slow down communications;

rather, it increases the likelihood that the message received is the same as the message sent.

CRC Series, Part 2: CRC Mathematics and Theory

Sun, 2007-12-02 15:58 - webmaster

by Michael Barr

Checksum algorithms based solely on addition are easy to implement and can be executed efficiently on any microcontroller.

However, many common types of transmission errors cannot be detected when such simple checksums are used.

This article describes a stronger type of checksum, commonly known as a CRC.

A cyclic redundancy check (CRC) is is based on division instead of addition.

The error detection capabilities of a CRC make it a much stronger checksum and,

therefore, often worth the price of additional computational complexity.

Additive checksums are error detection codes as opposed to error correction codes.

A mismatch in the checksum will tell you there's been an error but not where or how to fix it.

In implementation terms, there's not much difference between an error detection code and an error correction code.

In both cases, you take the message you want to send, compute some mathematical function over its bits (usually called a checksum),

and append the resulting bits to the message during transmission.

Error Correction

The difference between error detection and error correction lies primarily in what happens next.

If the receiving system detects an error in the packet--for example, the received checksum bits do not accurately describe the received message bits

--it may either discard the packet and request a retransmission (error detection)

or attempt to repair the damage on its own (error correction).

If packet repairs are to be attempted, the checksum is said to be an error correcting code.

The key to repairing corrupted packets is a stronger checksum algorithm.

Specifically, what's needed is a checksum algorithm that distributes the set of valid bit sequences randomly

and evenly across the entire set of possible bit sequences.

For example, if the minimum number of bits that must change to turn any one valid packet into some other valid packet is seven,

then any packet with three or fewer bit inversions can be corrected automatically by the receiver.

(If four bit errors occur during transmission, the packet will seem closer to some other valid packet with only three errors in it.)

In this case, error correction can only be done for up to three bit errors, while error detection can be done for up to six.

This spreading of the valid packets across the space of possible packets can be measured by the Hamming distance,

which is the number of bit positions in which any two equal-length packets differ.

In other words, it's the number of bit errors that must occur if one of those packets is to be incorrectly received as the other.

A simple example is the case of the two binary strings 1001001 and 1011010,

which are separated by a Hamming distance of three.

(To see which bits must be changed, simply XOR the two strings together and note the bit positions that are set.

In our example, the result is 0010011.)

The beauty of all this is that the mere presence of an error detection or correction code

within a packet means that not all of the possible packets are valid.

Figure 1 shows what a packet looks like after a checksum has been appended to it.

Since the checksum bits contain redundant information (they are completely a function of the message bits that precede them),

not all of the 2^(m+c) possible packets are valid packets.

In fact, the stronger the checksum algorithm used, the greater the number of invalid packets will be.

Figure 1. A packet of information including checksum

By adjusting the ratio of the lengths m and c and carefully selecting the checksum algorithm,

we can increase the number of bits that must be in error for any one valid packet

to be inadvertently changed into another valid packet during transmission or storage and,

hence, the likelihood of successful transmission.

In essence, what we want to do is to maximize the "minimum Hamming distance across the entire set of valid packets."

In other words, to distribute the set of 2^m valid packets as evenly as possible across the set of possible bit sequences of length m + c.

This has the useful real-world effect of increasing the percentage of detectable and/or correctable errors.

Binary Long Division

It turns out that once you start to focus on maximizing the "minimum Hamming distance across the entire set of valid packets,"

it becomes obvious that simple checksum algorithms based on binary addition don't have the necessary properties.

A change in one of the message bits does not affect enough of the checksum bits during addition.

Fortunately, you don't have to develop a better checksum algorithm on your own.

Researchers figured out long ago that modulo-2 binary division is the simplest mathematical operation

that provides the necessary properties for a strong checksum.

All of the CRC formulas you will encounter are simply checksum algorithms based on modulo-2 binary division.

Though some differences exist in the specifics across different CRC formulas, the basic mathematical process is always the same:

The message bits are appended with c zero bits; this augmented message is the dividend
A predetermined c+1-bit binary sequence, called the "generator polynomial", is the divisor
The checksum is the c-bit remainder that results from the division operation

In other words, you divide the augmented message by the generator polynomial,

discard the quotient, and use the remainder as your checksum.

It turns out that the mathematically appealing aspect of division is that remainders fluctuate rapidly as small numbers of bits within the message are changed.

Sums, products, and quotients do not share this property.

To see what I mean, look at the example of modulo-2 division in Figure 2.

In this example, the message contains eight bits while the checksum is to have four bits.

As the division is performed, the remainder takes the values

0111, 1111, 0101, 1011, 1101, 0001, 0010, and,

finally, 0100.

The final remainder becomes the checksum for the given message.

Figure 2. An example of modulo-2 binary division

For most people, the overwhelmingly confusing thing about CRCs is the implementation.

Knowing that all CRC algorithms are simply long division algorithms in disguise doesn't help.

Modulo-2 binary division doesn't map well to the instruction sets of general-purpose processors.

So, whereas the implementation of a checksum algorithm based on addition is straightforward,

the implementation of a binary division algorithm with an m+c-bit numerator and a c+1-bit denominator is nowhere close. [1]

For one thing, there aren't generally any m+c or c+1-bit registers in which to store the operands.

You will learn how to deal with this problem in the next article, where I talk about various software implementations of the CRC algorithms.

For now, let's just focus on their strengths and weaknesses as potential checksums.

Generator Polynomials

Why is the predetermined c+1 bits divisor that's used to calculate a CRC called a generator polynomial?

In my opinion, far too many explanations of CRCs actually try to answer that question.

This leads their authors and readers down a long path that involves tons of detail about polynomial arithmetic and the mathematical basis for the usefulness of CRCs.

This academic stuff is not important for understanding CRCs sufficiently to implement and/or use them and serves only to create potential confusion.

So I'm not going to answer that question here. [2]

Suffice it to say here only that the divisor is sometimes called a generator polynomial and that you should never make up the divisor's value on your own.

Several mathematically well-understood generator polynomials have been adopted as parts of various international communications standards;

you should always use one of those.

If you have a background in polynomial arithmetic then you know that certain generator polynomials are better than others for producing strong checksums.

The ones that have been adopted internationally are among the best of these.

Table 1 lists some of the most commonly used generator polynomials for 16- and 32-bit CRCs.

Remember that the width of the divisor is always one bit wider than the remainder.

So, for example, you'd use a 17-bit generator polynomial whenever a 16-bit checksum is required.

	Checksum Width	Generator Polynomial
CRC-CCITT	16 bits	10001000000100001
CRC-16	16 bits	11000000000000101
CRC-32	32 bits	100000100110000010001110110110111

Table 1. International standard CRC polynomials

As is the case with other types of checksums, the width of the CRC plays an important role in the error detection capabilities of the algorithm.

Ignoring special types of errors that are always detected by a particular checksum algorithm, the percentage of detectable errors is limited strictly by the width of a checksum.

A checksum of c bits can only take one of 2^cunique values.

Since the number of possible messages is significantly larger than that, the potential exists for two or more messages to have an identical checksum.

If one of those messages is somehow transformed into one of the others during transmission,

the checksum will appear correct and the receiver will unknowingly accept a bad message.

The chance of this happening is directly related to the width of the checksum.

Specifically, the chance of such an error is 1/2^c. Therefore, the probability of any random error being detected is 1-1/2^c.

To repeat, the probability of detecting any random error increases as the width of the checksum increases.

Specifically, a 16-bit checksum will detect 99.9985% of all errors.

This is far better than the 99.6094% detection rate of an eight-bit checksum, but not nearly as good as the 99.9999% detection rate of a 32-bit checksum.

All of this applies to both CRCs and addition-based checksums.

What really sets CRCs apart, however, is the number of special cases that can be detected 100% of the time.

For example, I pointed out last month that two opposite bit inversions (one bit becoming 0, the other becoming 1)

in the same column of an addition would cause the error to be undetected. Well, that's not the case with a CRC.

By using one of the mathematically well-understood generator polynomials like those in Table 1 to calculate a checksum,

it's possible to state that the following types of errors will be detected without fail:

A message with any one bit in error
A message with any two bits in error (no matter how far apart, which column, and so on)
A message with any odd number of bits in error (no matter where they are)
A message with an error burst as wide as the checksum itself

The first class of detectable error is also detected by an addition-based checksum, or even a simple parity bit.

However, the middle two classes of errors represent much stronger detection capabilities than those other types of checksum.

The fourth class of detectable error sounds at first to be similar to a class of errors detected by addition-based checksums, but in the case of CRCs,

any odd number of bit errors will be detected.

So the set of error bursts too wide to detect is now limited to those with an even number of bit errors.

All other types of errors fall into the relatively high 1-1/2^c probability of detection.

Ethernet, SLIP, and PPP

Ethernet, like most physical layer protocols, employs a CRC rather than an additive checksum.

Specifically, it employs the CRC-32 algorithm. The likelihood of an error in a packet sent over Ethernet being undetected is,

therefore, extremely low. Many types of common transmission errors are detected 100% of the time,

with the less likely ones detected 99.9999% of the time.

Even if an error would somehow manage to get through at the Ethernet layer, it would probably be detected at the IP layer checksum

(if the error is in the IP header) or in the TCP or UDP layer checksum above that.

After all the chances of two or more different checksum algorithms not detecting the same error is extremely remote.

However, many embedded systems that use TCP/IP will not employ Ethernet.

Instead, they will use either the serial line Internet protocol (SLIP) or point-to-point protocol (PPP)

to send and receive IP packets directly over a serial connection of some sort.

Unfortunately, SLIP does not add a checksum or a CRC to the data from the layers above.

So unless a pair of modems with error correction capabilities sits in between the two communicating systems,

any transmission errors must hope to be detected by the relatively weak, addition-based Internet checksum described last month.

The newer, compressed SLIP (CSLIP) shares this weakness with its predecessor.

PPP, on the other hand, does include a 16-bit CRC in each of its frames, which can carry the same maximum size IP packet as an Ethernet frame.

So while PPP doesn't offer the same amount of error detection capability as Ethernet,

by using PPP you'll at least avoid the much larger number of undetected errors that may occur with SLIP or CSLIP.

Read my article on CRC calculations in C, to learn about various software implementations of CRCs.

We'll start with an inefficient, but comprehendible, implementation and work to gradually increase its efficiency.

You'll see then that the desire for an efficient implementation is the cause of much of the confusion surrounding CRCs. In the meantime, stay connected..

Footnotes

[1] Implementing modulo-2 division is much more straightforward in hardware than it is in software. You simply need to shift the message bits through a linear feedback shift register as they are received. The bits of the divisor are represented by physical connections in the feedback paths. Due to the increased simplicity and efficiency, CRCs are usually implemented in hardware whenever possible.

[2] If you really want to understand the underlying mathematical basis for CRCs, I recommend the following reference: Bertsekas, Dimitri and Robert Gallager. Data Networks, second ed. Inglewood Cliffs, NJ: Prentice-Hall, 1992, pp. 61-64.

CRC Series, Part 3: CRC Implementation Code in C/C++

Sun, 2007-12-02 16:54 - webmaster

by Michael Barr

CRCs are among the best checksums available to detect and/or correct errors in communications transmissions.

Unfortunately, the modulo-2 arithmetic used to compute CRCs doesn't map easily into software.

This article shows how to implement an efficient CRC in C.

I'm going to complete my discussion of checksums by showing you how to implement CRCs in software.

I'll start with a naive implementation and gradually improve the efficiency of the code as I go along.

However, I'm going to keep the discussion at the level of the C language,

so further steps could be taken to improve the efficiency of the final code simply by moving into the assembly language of your particular processor.

For most software engineers, the overwhelmingly confusing thing about CRCs is their implementation.

Knowing that all CRC algorithms are simply long division algorithms in disguise doesn't help.

Modulo-2 binary division doesn't map particularly well to the instruction sets of off-the-shelf processors.

For one thing, generally no registers are available to hold the very long bit sequence that is the numerator.

For another, modulo-2 binary division is not the same as ordinary division.

So even if your processor has a division instruction, you won't be able to use it.

Modulo-2 Binary Division

Before writing even one line of code, let's first examine the mechanics of modulo-2 binary division.

We'll use the example in Figure 1 to guide us.

The number to be divided is the message augmented with zeros at the end.

The number of zero bits added to the message is the same as the width of the checksum (what I call c);

in this case four bits were added. The divisor is a c+1-bit number known as the generator polynomial.

Figure 1. An example of modulo-2 binary division

The modulo-2 division process is defined as follows:

Call the uppermost c+1 bits of the message the remainder
Beginning with the most significant bit in the original message and for each bit position that follows, look at the c+1 bit remainder:
- If the most significant bit of the remainder is a one, the divisor is said to divide into it.
  If that happens (just as in any other long division) it is necessary to indicate a successful division
  in the appropriate bit position in the quotient and to compute the new remainder. In the case of modulo-2 binary division, we simply:
  - Set the appropriate bit in the quotient to a one, and
  - XOR the remainder with the divisor and store the result back into the remainder
- Otherwise (if the first bit is not a one):
  - Set the appropriate bit in the quotient to a zero, and
  - XOR the remainder with zero (no effect)
- Left-shift the remainder, shifting in the next bit of the message. The bit that's shifted out will always be a zero, so no information is lost.

The final value of the remainder is the CRC of the given message.

What's most important to notice at this point is that we never use any of the information in the quotient, either during or after computing the CRC.

So we won't actually need to track the quotient in our software implementation.

Also note here that the result of each XOR with the generator polynomial is a remainder that has zero in its most significant bit.

So we never lose any information when the next message bit is shifted into the remainder.

Bit by Bit

Listing 1 contains a naive software implementation of the CRC computation just described.

It simply attempts to implement that algorithm as it was described above for this one particular generator polynomial.

Even though the unnecessary steps have been eliminated, it's extremely inefficient.

Multiple C statements (at least the decrement and compare, binary AND, test for zero, and left shift operations)

must be executed for each bit in the message.

Given that this particular message is only eight bits long, that might not seem too costly.

But what if the message contains several hundred bytes, as is typically the case in a real-world application?

You don't want to execute dozens of processor opcodes for each byte of input data

#define POLYNOMIAL 0xD8  /* 11011 followed by 0's */

uint8_t crcNaive( uint8_t const message )
{
  uint8_t remainder;
  
  /*
   * Initially, the dividend is the remainder.
   */
  remainder = message;
  
  /*
   * For each bit position in the message....
   */
  for ( uint8_t bit = 8; bit > 0; --bit )
  {
    /*
     * If the uppermost bit is a 1...
     */
    if ( remainder & 0x80 )
    {
      /*
       * XOR the previous remainder with the divisor.
       */
      remainder ^= POLYNOMIAL;
    }
    
    /*
     * Shift the next bit of the message into the remainder.
     */
    remainder = ( remainder << 1 );
  }
  
  /*
   * Return only the relevant bits of the remainder as CRC.
   */
  return ( remainder >> 4 );
  
} /* crcNaive() */

Listing 1. A naive CRC implementation in C

Code Cleanup

Before we start making this more efficient, the first thing to do is to clean this naive routine up a bit.

In particular, let's start making some assumptions about the applications in which it will most likely be used.

First, let's assume that our CRCs are always going to be 8-, 16-, or 32-bit numbers.

In other words, that the remainder can be manipulated easily in software.

That means that the generator polynomials will be 9, 17, or 33 bits wide, respectively.

At first it seems we may be stuck with unnatural sizes and will need special register combinations, but remember these two facts:

The most significant bit of any generator polynomial is always a one
The uppermost bit of the XOR result is always zero and promptly shifted out of the remainder

Since we already have the information in the uppermost bit and

we don't need it for the XOR, the polynomial can also be stored in an 8-, 16-, or 32-bit register.

We can simply discard the most significant bit. The register size that we use will always be equal to the width of the CRC we're calculating.

As long as we're cleaning up the code, we should also recognize that most CRCs are computed over fairly long messages.

The entire message can usually be treated as an array of unsigned data bytes.

The CRC algorithm should then be iterated over all of the data bytes, as well as the bits within those bytes.

Test Your Embedded C Programming Skills

The result of making these two changes is the code shown in Listing 2.

This implementation of the CRC calculation is still just as inefficient as the previous one.

However, it is far more portable and can be used to compute a number of different CRCs of various widths.

/*
 * The width of the CRC calculation and result.
 * Modify the typedef for a 16 or 32-bit CRC standard.
 */
typedef uint8_t crc;

#define WIDTH  (8 * sizeof(crc))
#define TOPBIT (1 << (WIDTH - 1))

crc crcSlow( uint8_t const message[ ], int nBytes )
{
  crc remainder = 0;
  
  /*
   * Perform modulo-2 division, a byte at a time.
   */
  for ( int byte = 0; byte < nBytes; ++byte )
  {
    /*
     * Bring the next byte into the remainder.
     */
    remainder ^= ( message[ byte ] << ( WIDTH - 8 ) );
    
    /*
     * Perform modulo-2 division, a bit at a time.
     */
    for ( uint8_t bit = 8; bit > 0; --bit )
    {
      /*
       * Try to divide the current data bit.
       */
      if ( remainder & TOPBIT )
      {
        remainder = ( remainder << 1 ) ^ POLYNOMIAL;
      }
      else
      {
        remainder = ( remainder << 1 );
      }
    }
  }
  
  /*
   * The final remainder is the CRC result.
   */
  return ( remainder );
  
} /* crcSlow() */

Listing 2. A more portable but still naive CRC implementation

Byte by Byte

The most common way to improve the efficiency of the CRC calculation is to throw memory at the problem.

For a given input remainder and generator polynomial, the output remainder will always be the same.

If you don't believe me, just reread that sentence as "for a given dividend and divisor, the remainder will always be the same."

It's true.

So it's possible to precompute the output remainder for each of the possible byte-wide input remainders and store the results in a lookup table.

That lookup table can then be used to speed up the CRC calculations for a given message.

The speedup is realized because the message can now be processed byte by byte, rather than bit by bit.

Improve Your Embedded Programming Skills

The code to precompute the output remainders for each possible input byte is shown in Listing 3.

The computed remainder for each possible byte-wide dividend is stored in the array crcTable[].

In practice, the crcInit() function could either be called during the target's initialization sequence (thus placing crcTable[] in RAM)

or it could be run ahead of time on your development workstation with the results stored in the target device's ROM.

crc crcTable[ 256 ];

void crcInit( void )
{
  crc remainder;
  
  /*
   * Compute the remainder of each possible dividend.
   */
  for ( int dividend = 0; dividend < 256; ++dividend )
  {
    /*
     * Start with the dividend followed by zeros.
     */
    remainder = dividend << ( WIDTH - 8 );
    
    /*
     * Perform modulo-2 division, a bit at a time.
     */
    for ( uint8_t bit = 8; bit > 0; --bit )
    {
      /*
       * Try to divide the current data bit.
       */
      if ( remainder & TOPBIT )
      {
        remainder = ( remainder << 1 ) ^ POLYNOMIAL;
      }
      else
      {
        remainder = ( remainder << 1 );
      }
    }
    
    /*
     * Store the result into the table.
     */
    crcTable[ dividend ] = remainder;
  }
  
} /* crcInit() */

Listing 3. Computing the CRC lookup table

Of course, whether it is stored in RAM or ROM, a lookup table by itself is not that useful.

You'll also need a function to compute the CRC of a given message that is somehow able to make use of the values stored in that table.

Without going into all of the mathematical details of why this works,

suffice it to say that the previously complicated modulo-2 division can now be implemented as a series of lookups and XORs.

(In modulo-2 arithmetic, XOR is both addition and subtraction.)

Follow a Bug-Killing Embedded C Coding Standard

A function that uses the lookup table contents to compute a CRC more efficiently is shown in Listing 4.

The amount of processing to be done for each byte is substantially reduced.

crc crcFast( uint8_t const message[ ], int nBytes )
{
  uint8_t data;
  crc remainder = 0;
  
  /*
   * Divide the message by the polynomial, a byte at a time.
   */
  for ( int byte = 0; byte < nBytes; ++byte )
  {
    data = message[ byte ] ^ ( remainder >> ( WIDTH - 8 ) );
    remainder = crcTable[ data ] ^ ( remainder << 8 );
  }
  
  /*
   * The final remainder is the CRC.
   */
  return ( remainder );
  
} /* crcFast() */

Listing 4. A more efficient, table-driven, CRC implementation

As you can see from the code in Listing 4, a number of fundamental operations (left and right shifts, XORs, lookups, and so on)

still must be performed for each byte even with this lookup table approach.

So to see exactly what has been saved (if anything) I compiled both crcSlow() and crcFast()

with IAR(link is external)'s C compiler for the PIC family of eight-bit RISC processors. ¹

I figured that compiling for such a low-end processor would give us a good worst-case comparison for the numbers of instructions

to do these different types of CRC computations. The results of this experiment were as follows:

crcSlow(): 185 instructions per byte of message data
crcFast(): 36 instructions per byte of message data

So, at least on one processor family, switching to the lookup table approach results in a more than five-fold performance improvement.

That's a pretty substantial gain considering that both implementations were written in C.

A bit more could probably be done to improve the execution speed of this algorithm

if an engineer with a good understanding of the target processor were assigned to hand-code or tune the assembly code.

My somewhat-educated guess is that another two-fold performance improvement might be possible.

Actually achieving that is, as they say in textbooks, left as an exercise for the curious reader.

CRC standards and parameters

Now that we've got our basic CRC implementation nailed down, I want to talk about the various types of CRCs that you can compute with it.

As I mentioned last month, several mathematically well understood and internationally standardized CRC generator polynomials exist

and you should probably choose one of those, rather than risk inventing something weaker.

In addition to the generator polynomial, each of the accepted CRC standards also includes certain other parameters that describe how it should be computed.

Table 1 contains the parameters for three of the most popular CRC standards.

Two of these parameters are the "initial remainder" and the "final XOR value".

The purpose of these two c-bit constants is similar to the final bit inversion step added to the sum-of-bytes checksum algorithm.

Each of these parameters helps eliminate one very special, though perhaps not uncommon, class of ordinarily undetectable difference.

In effect, they bulletproof an already strong checksum algorithm.

	CRC-CCITT	CRC-16	CRC-32
Width	16 bits	16 bits	32 bits
(Truncated) Polynomial	0x1021	0x8005	0x04C11DB7
Initial Remainder	0xFFFF	0x0000	0xFFFFFFFF
Final XOR Value	0x0000	0x0000	0xFFFFFFFF
Reflect Data?	No	Yes	Yes
Reflect Remainder?	No	Yes	Yes
Check Value	0x29B1	0xBB3D	0xCBF43926

Table 1. Computational parameters for popular CRC standards

To see what I mean, consider a message that begins with some number of zero bits.

The remainder will never contain anything other than zero until the first one in the message is shifted into it.

That's a dangerous situation, since packets beginning with one or more zeros may be completely legitimate

and a dropped or added zero would not be noticed by the CRC.

(In some applications, even a packet of all zeros may be legitimate!)

The simple way to eliminate this weakness is to start with a nonzero remainder.

The parameter called initial remainder tells you what value to use for a particular CRC standard.

And only one small change is required to the crcSlow() and crcFast() functions:

crc remainder = INITIAL_REMAINDER;

The final XOR value exists for a similar reason.

To implement this capability, simply change the value that's returned by crcSlow() and crcFast() as follows:

 return (remainder ^ FINAL_XOR_VALUE);

If the final XOR value consists of all ones (as it does in the CRC-32 standard),

this extra step will have the same effect as complementing the final remainder.

However, implementing it this way allows any possible value to be used in your specific application.

In addition to these two simple parameters, two others exist that impact the actual computation.

These are the binary values "reflect data" and "reflect remainder".

The basic idea is to reverse the bit ordering of each byte within the message and/or the final remainder.

The reason this is sometimes done is that a good number of the hardware CRC implementations operate

on the "reflected" bit ordering of bytes that is common with some UARTs.

Two slight modifications of the code are required to prepare for these capabilities.

What I've generally done is to implement one function and two macros.

This code is shown in Listing 5.

The function is responsible for reflecting a given bit pattern. The macros simply call that function in a certain way

#define REFLECT_DATA(X)       ((uint8_t) reflect((X), 8))
#define REFLECT_REMAINDER(X)  ((crc) reflect((X), WIDTH))

uint32_t reflect( uint32_t data, uint8_t nBits )
{
  uint32_t reflection = 0;
  
  /*
   * Reflect the data about the center bit.
   */
  for ( uint8_t bit = 0; bit < nBits; ++bit )
  {
    /*
     * If the LSB bit is set, set the reflection of it.
     */
    if ( data & 0x01 )
    {
      reflection |= ( 1 << ( ( nBits - 1 ) - bit ) );
    }
    
    data = ( data >> 1 );
  }
  
  return ( reflection );
  
} /* reflect() */

Listing 5. Reflection macros and function

By inserting the macro calls at the two points that reflection may need to be done,

it is easier to turn reflection on and off.

To turn either kind of reflection off, simply redefine the appropriate macro as (X).

That way, the unreflected data byte or remainder will be used in the computation, with no overhead cost.

Also note that for efficiency reasons, it may be desirable to compute the reflection of all of the 256 possible data bytes

in advance and store them in a table, then redefine the REFLECT_DATA() macro to use that lookup table.

Tested, full-featured implementations of both crcSlow() and crcFast() are available for

download.

These implementations include the reflection capabilities just described and can be used to implement any parameterized CRC formula.

Simply change the constants and macros as necessary.

The final parameter that I've included in Table 1 is a "check value" for each CRC standard.

This is the CRC result that's expected for the simple ASCII test message "123456789".

To test your implementation of a particular standard, simply invoke your CRC computation on that message and check the result:

crcInit();

checksum = crcFast("123456789", 9);

f checksum has the correct value after this call, then you know your implementation is correct.

This is a handy way to ensure compatibility between two communicating devices with different CRC implementations or implementors.

Acknowledgement

Through the years, each time I've had to learn or relearn something about the various CRC standards or their implementation,

I've referred to the paper "A Painless Guide to CRC Error Detection Algorithms, 3rd Edition(link is external)" by Ross Williams.

There are a few holes that I've hoped for many years that the author would fill with a fourth edition,

but all in all it's the best coverage of a complex topic that I've seen.

Many thanks to Ross for sharing his expertise with others and making several of my networking projects possible.

Free Source Code in C and C++

The source code for these CRC computations is placed into the public domain and is available in electronic form at

http://www.barrgroup.com/code/crc.zip.

Inspired by the treatment of CRC computations here and in Ross Williams' paper, a gentleman named Daryle Walker

<darylew@mac.com(link sends e-mail)> has implemented some very nice C++ class and function templates for doing the same.

The entire library, which is distributed in source code form and in the public domain, is available at

http://www.boost.org/libs/crc/(link is external).

Footnotes

[1] I first modified both functions to use unsigned char instead of int for variables nBytes and byte.

This effectively caps the message size at 256 bytes, but I thought that was probably a pretty typical compromise for use on an eight-bit processor.

I also had the compiler optimize the resulting code for speed, at its highest setting.

I then looked at the actual assembly code produced by the compiler and counted the instructions inside the outer for loop in both cases.

In this experiment, I was specifically targeting the PIC16C67 variant of the processor, using

IAR Embedded Workbench(link is external) 2.30D (PICmicro engine 1.21A).

This column was published in the January 2000 issue of

Embedded Systems Programming(link is external).

If you wish to cite the article in your own work, you may find the following MLA-style information helpful:

Barr, Michael. "Slow and Steady Never Lost the Race," Embedded Systems Programming, January 2000, pp. 37-46.

posted @ 2015-06-27 13:46 IAmAProgrammer 阅读(1429) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

CRC 详解

CRC Series, Part 1: Additive Checksums

Parity Bits

Checksums

The Internet Checksum

Further reading

CRC Series, Part 2: CRC Mathematics and Theory

Error Correction

Binary Long Division

Generator Polynomials

Ethernet, SLIP, and PPP

Footnotes

CRC Series, Part 3: CRC Implementation Code in C/C++

Modulo-2 Binary Division

Bit by Bit

Code Cleanup

Byte by Byte

CRC standards and parameters

Acknowledgement

Free Source Code in C and C++

Footnotes