低差异序列 (low-discrepancy sequences)之Halton序列均匀产生多维随机数的介绍与实现
Halton序列
在统计学中,Halton序列是用于生成空间中的点的序列,如Monte Carlo模拟的数值方法,虽然这些序列是确定性的,但它们的差异性很低,也就是说,在许多方面看起来是随机的。它们在1960年首次提出,是准随机数列的一个例子。它们概括了一维Van der Corput序列
用于生成\(R^2\)中(0,1)x(0,1)点的Halton序列的例子
Halton数列是以质数为基的确定性方法构造的。举个简单的例子,让我们把Halton序列的一个维度基于2,另一个基于3。为了生成2的序列,我们首先将区间\((0,1)\)分成两半,然后分成四分之一、八分之一等,这就产生了
等价的,这个序列的第n个数字是用二进制表示的数字n,倒过来,并写在小数点之后。这对任何基数都是如此。举个例子,要找到上述序列的第六个元素,我们要写\(6=1*2^2+1*2^1+0*2^0=110_2\),可以倒置并放在小数点之后,得到\(0.011_2=0*2^{-1}+1*2^{-2}+1*2^{-3}=\frac{3}{8}\)。所以上面的序列与\(0.1_2,0.01_2,0.11_2,0.001_2,0.101_2,0.011_2,0.111_2,0.0001_2,0.1001_2\)相同
为了生成3的序列,我们把区间\((0,1)\)分成三份,然后是九份,二十七份,等等...这就产生了(同理表示成三进制的数,然后进行相应操作)
当我们把它们配对起来时,我们会得到一个单位方格中的点的序列。
尽管标准的Halton序列在低维情况下表现的很好,但由高质数生成的序列之间存在相关问题。例如,如果我们从质数17和19开始,前16个对点数:\((\frac{1}{17},\frac{1}{19}),(\frac{2}{17},\frac{2}{19}),(\frac{3}{17},\frac{3}{19})...(\frac{16}{17},\frac{16}{19})\)具有完美的线性相关性。为了避免这种情况,通常会删除前20个条目,或者根据选择的指数来删除其他预定的数量。还提出了其他几种办法,最突出的解决方案之一是scrambled Halton序列,它使用在构建标准序列中使用的系数的排列组合。另一个解决方案是leaped Halton,它会在标准序列中跳过点(例如,只有每409个点(也可以是其他没有在Halton核心序列中使用的质数),才能取得显著的改进)。
实现
伪代码
algorithm Halton-Sequence is
inputs: index i
base b
output: result r
f⬅1
r⬅0
while i > 0 do
f⬅f/b
r⬅r+f * (i mod b)
i⬅[i/b]
return r
下面的生成器函数 generator function (Python)中给出了另一种实现方式,它可以产生以\(b\)为基数的Halton序列的后续数字。这种算法在内部只使用整数,这使得它对四舍五入的错误具有很强的健壮性。
def halton(b):
"""Generator function for Halton sequence."""
n, d = 0, 1
while True:
x = d - n
if x == 1:
n = 1
d *= b
else:
y = d // b
while x <= y:
y //= b
n = (b + 1) * y - x
yield n / d
参照
补充原文
原文中陈述了很多具体的例子,而缺乏了一些Halton序列本身的说明,使用场景、以及与其他序列使用对比的差异,故在此处进行补充,更详细的介绍可参考https://zhuanlan.zhihu.com/p/20197323
Halton和Hammersley可以生成在无穷维度上分布均匀的点集,它们都基于Van der Corput序列
Halton序列的定义很简单:
既是每一个维度都是一个基于不同底数\(b_n\)的Van der Corput序列,其中\(b_1...b_n\)互为质数(例如第\(1\)到第\(n\)个质数)
Hammersley点集的定义和Halton非常相似
以下是Hammersley点集的定义
唯一不同的就是把第一个维度变成\(\frac{i}{N}\),其中\(i\)为样本点的索引,\(N\)为样本点集中点的个数。根据定义,Hammersley点集只能生成固定数目个样本,而Halton序列则可以生成无穷个样本(当然在计算机里我们只有有限的bit去表示有限个样本点)

上面左边的图为第1-100个Halton序列中的二维的样本点,\((\varPhi_2(i),\varPhi_3(i))^{99}_{i=0}\),右边则为数量为100的二维Hammersley样本点集,\((\frac{i}{100},\varPhi_2(i))^{99}_{i=0}\)。可以看出来它们的分布都远比一般的伪随机数更加均匀。Hammersley的差异性比Halton更稍低一些,但是代价是必须预先知道点的数量,并且一旦固定无法更改虚幻引擎4中对环境贴图的Filter采样就是用的点集大小固定为1024的Hammersley点集。Halton虽然差异性稍高,但可以不受限制的生成无穷多个点,更适合于没有固定样本个数的应用,例如任何progressive或者adaptive的过程。
基于radical inversion的序列还都具有Stratified样本的性质。因为每一个维度都是一个radical inversion,所以每一维度都具有所有之前提到的radical inversion的性质。其中之一就是点集个数到达\(b^m\)个点时对\([0,1)\)会形成uniform的划分。下图是第1-12个Halton序列的二维点集,可以看出点0-7在X轴的投影和0-8在Y轴的投影都是均匀覆盖。这也意味着在样本数量等于每个维度底数的公倍数的适合,样本会自然在每个维度上底数的倍数的strata中自然的形成stratified采样。例如下图中的第0-5个点,刚好在图中落在2x3的strata中。

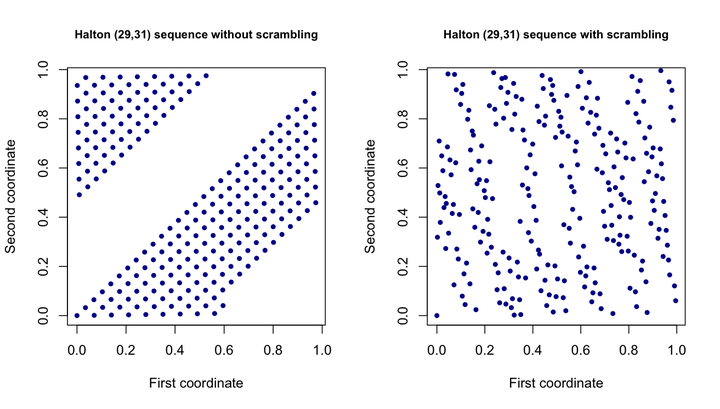
\(\frac{1}{29},\frac{2}{29},\frac{3}{29}...\)所以造成了点都集中落在了一条直线上面。解决这个问题的方法也很简单,Scrambling。Scrambling的方法有许多种,例如最简单的XOR Scrambling适用于以2为底数的序列。对于Halton来说,一个比较常用的方法是Faure Scrambling。
如上面的公式所写,Faure Scrambling的做法就是在做radical inverse的时候不直接将数字镜像到小数点右边,而在镜像前先把每个数字通过一个permutation\(\sigma _b\)转换成另一个数字。不同的底数\(b\)有不同的permutation\(\sigma\)。例如\(\sigma_4=[0,2,1,3]\)。至于\(\sigma_b\)如何具体计算这里不再展开,下一篇专栏在讲实现时会给出参考链接。这里值得一提的时Scrambling完全不会影响radical inversion序列分布的随机性,因为radical inversion会自然的将空间均等划分成底数\(b\)的整数次幂个部分,scrambling本质上就是在交换这些均等划分的部分,所以Scrambled后的序列依然具有radical inversion的性质。
实现
实现伪代码
double make_halton_sequence(int index, int base) {
double f = 1, r = 0;
while (index > 0) {
f = f / base;
r = r + f * (index % base);
index = index / base;
}
return r * randpoint_scale;
}
void halton_random()
{
// 此处讨论生成二维随机数,如要产生多维,base需要是不重复的质数即可
// 三维:base 2 3 5
for (uint i = 0u; i < max_num; ++i)
{
draw_points.emplace_back(make_halton_sequence(i, 2), make_halton_sequence(i, 3));
// 三维
draw_points.emplace_back(make_halton_sequence(i, 2), make_halton_sequence(i, 3)
, make_halton_sequence(i, 5));
}
}
Halton序列在底数较大的时候,样本个数会有很严重的correlation。所以需要采用Scrambling解决这个问题RadicalInverse的实现的效率依赖于一个循环,将索引Index的数字左右颠倒。这一步骤可以通过一次将多个连续数字的左右颠倒连同Faure Scrambling预计算出来,存在一个查找表里。运行的时候直接将索引的多个数字提取出来,然后直接查表得到结果。下面给出一段以5作为底数的Halton序列实现
详细做法可参考:HALTON The Halton Quasi Monte Carlo (QMC) Sequence
与Hammersley序列的对比
Hammersley序列的介绍与实现可参考这篇:
Halton序列无需在生成随机数之前,知道需要生成随机点的个数,但是在用一些比较大的质数作为底数时,Halton序列的分布在点的数量不那么多的时候并不会均匀的分布,只有当点的数量接近底数的幂的时候分布才会逐渐均匀
效果对比
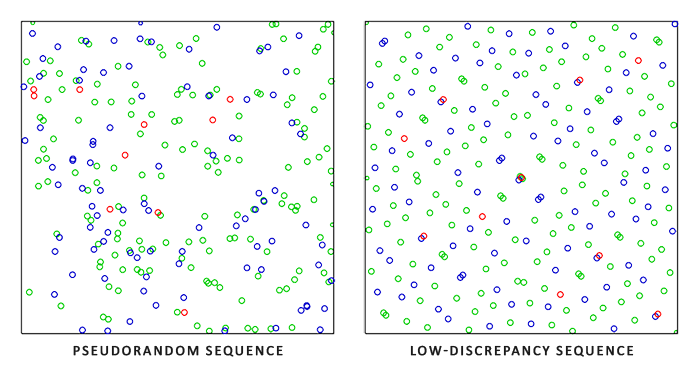
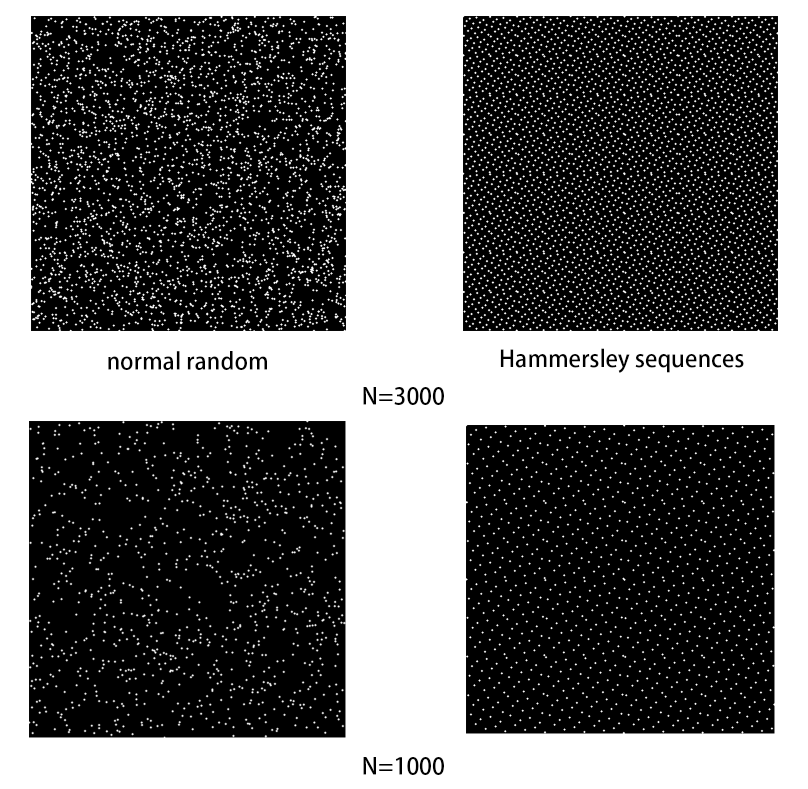
Halton序列比一般的伪随机数更加地分布均匀,因为此处是没有对Halton进行优化的,即没有Scrambling,可从另一幅图看到,Hammersley序列比未优化的Halton序列相对来说更加地均匀,但未优化的效果也可以说是比较不错的了

引用
翻译自:https://en.wikipedia.org/wiki/Halton_sequence
引用博客:
可拓展阅读:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号