14. ＜tag-数组和二分查找_2＞-lt.240-搜索二维矩阵 || + lt.633-平方数之和 +lt.69-Sqrt(x) 1

lt.240-搜索二维矩阵 ||

[案例需求]

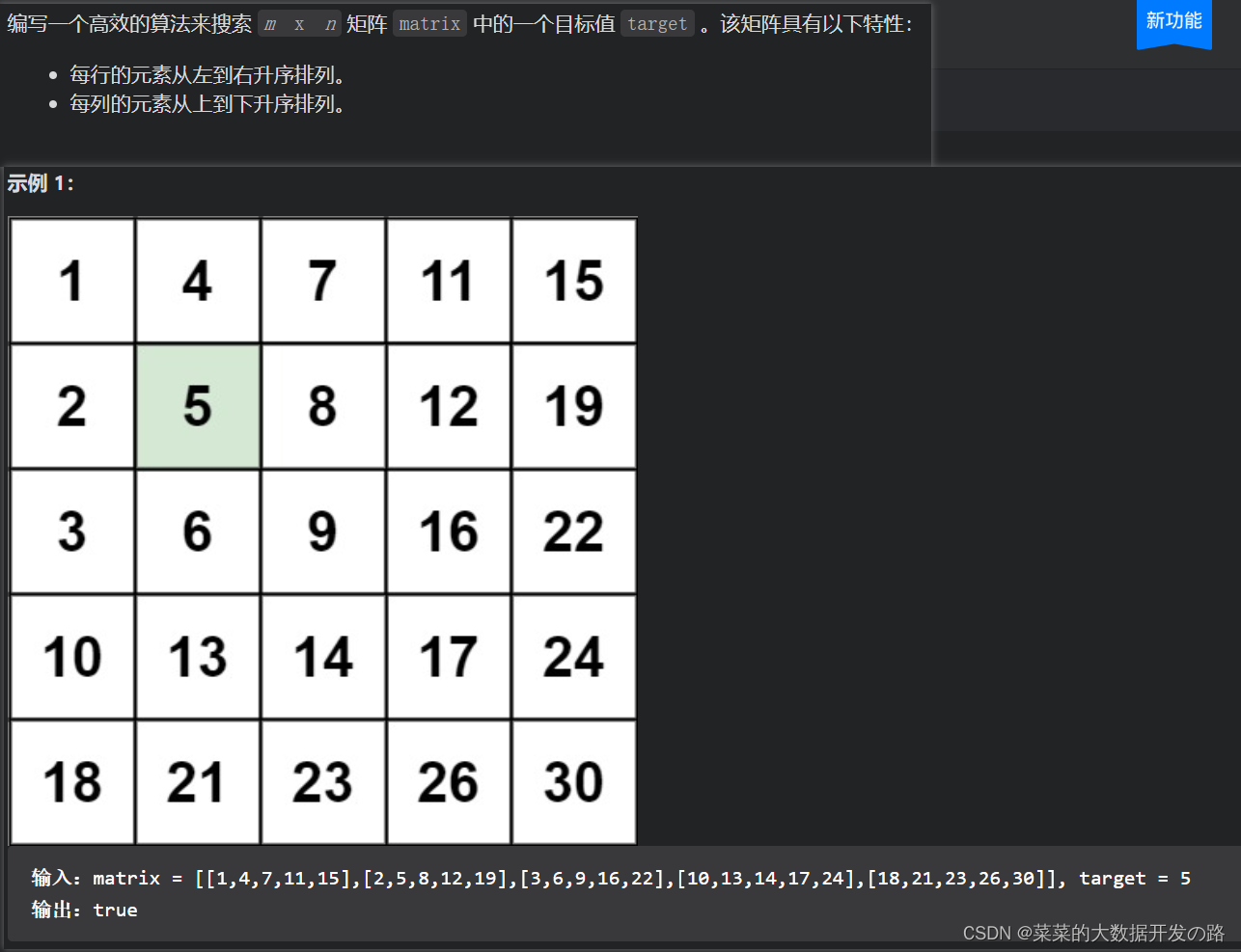
优化1. 二分查找法

[思路分析]

• 本题, 从基础的倒序遍历解法上来看, 跟之前做过的一道题lt.74-搜索二维矩阵完全类似

• 这里, 我们采用二分查找法解题;

• 要注意到的是: 与 lt.74-搜索二维矩阵不同，本题没有确保「每行的第一个整数大于前一行的最后一个整数」，因此我们无法采取「两次二分」的做法。只能退而求之，遍历行/列，然后再对列/行进行二分。

• 首先我们对二维数组遍历每一行, 跟倒序遍历相似

  • 1. 第一层循环, 我们遍历二维数组的每一行,
  • 2. 如果 某一行末尾的数 < target , 那么由于行升序的原因, 可以直接跳出本次遍历;
  • 3. 如果 某一行末尾的数 > target , 说明target可能是在这一行, 就在这一行进行二分查找, 取本行的第一个数作为left指针, 最后一个数作为right指针,
  • 4. 如果前面的二分查找没找到, 就继续下一行的循环;

[代码实现]

    class Solution {
        public boolean searchMatrix(int[][] matrix, int target) {
            //倒序遍历
            for(int i = 0; i < matrix.length; i++){
                int L = 0;
                int R = matrix[i].length - 1;
                
                if(matrix[i][R] < target) continue;

                while(L <= R){
                    int mid = L + (R - L)/2;
                    if(matrix[i][mid] == target){
                        return true;
                    }else if(matrix[i][mid] < target){
                        L = mid + 1;
                    }else if(matrix[i][mid] > target){
                        R = mid - 1;
                    }
                }
            }
            return false;
        }
    }

• 相比前面文章写道的倒序遍历, 其实提高并不是很大, 这里主要是因为采用倒序遍历跟二分法时, 我们都对 target > 每行末尾最后一个数的这样的行, 做了跳过本行的操作(因为每行是升序的嘛, 最后一个数都小于 target了, 哪还有向前遍历的需要啊), 而在target < 某一行末尾的最后一个数这样的行里, 我们才对行中的数进行倒序遍历(或二分查找), 倒序遍历和二分查找的差别就是在这样行里, 所以优化提升非常有限;

---

优化2. 利用单调性(把行升序和列升序两个条件同时利用起来)

[思路分析]

• 参考题解

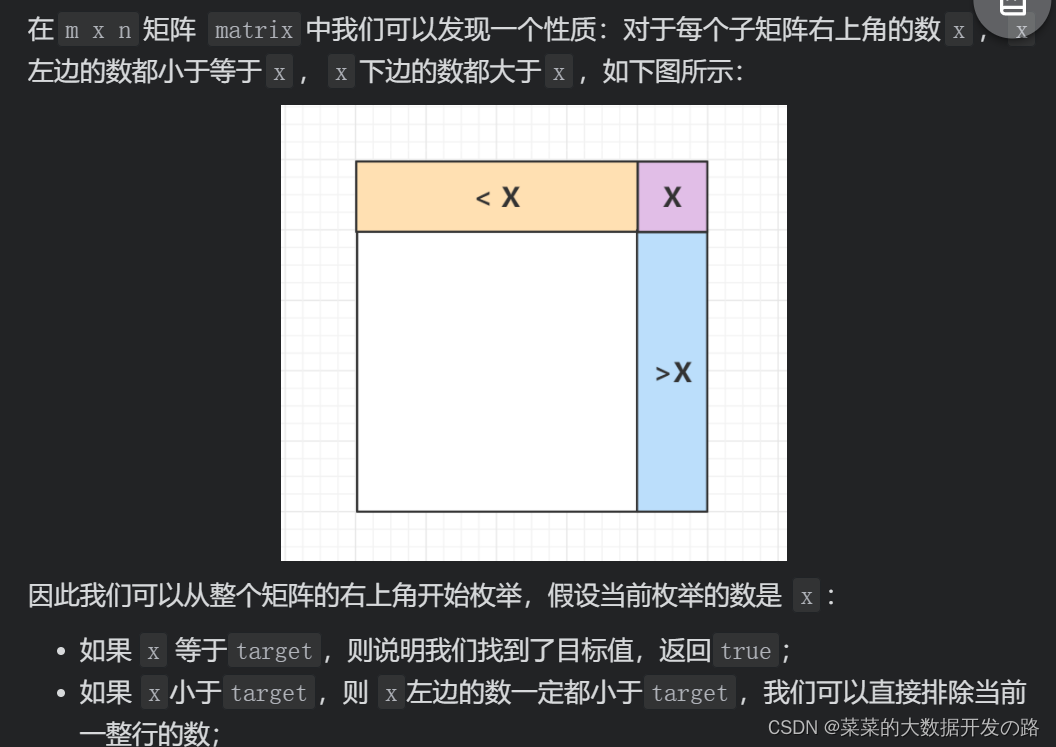
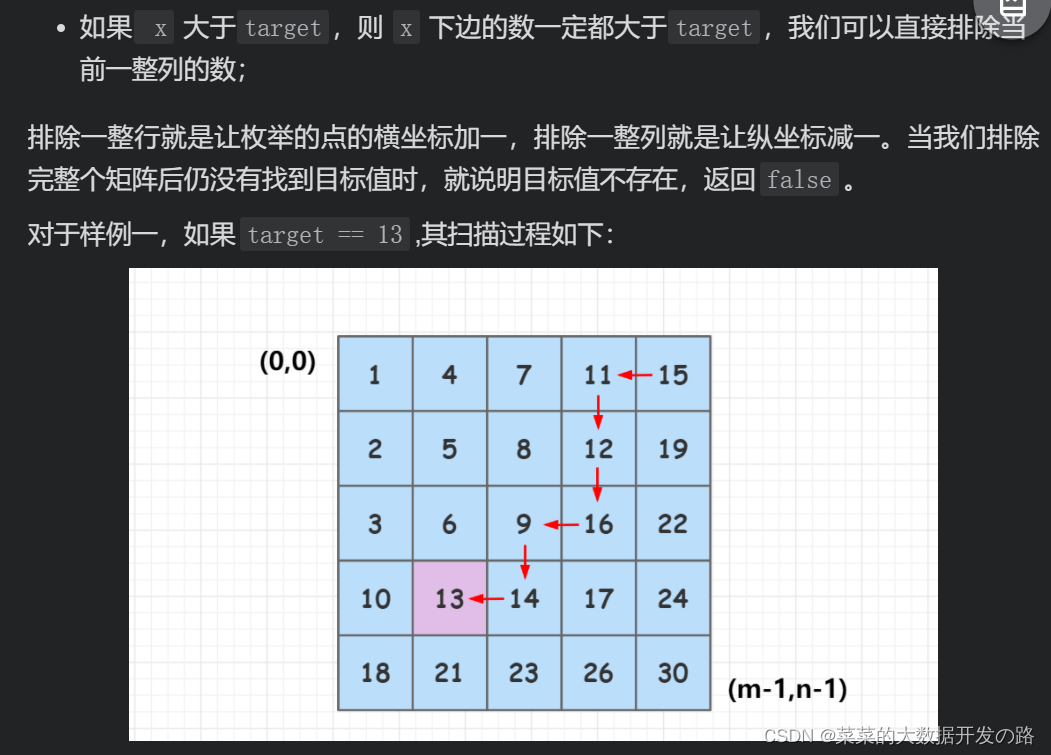
[代码实现]

//单调性
        int rowLen = matrix.length;
        int colLen = matrix[0].length;


        int i = 0;
        int j = colLen - 1;

        while(i < rowLen && j >=0){
            if(matrix[i][j] < target){
                i++;
            }else if(matrix[i][j] > target){
                j--;
            }else{
                return true;
            }
        }

        return false;

lt.633-平方数之和

[案例需求]

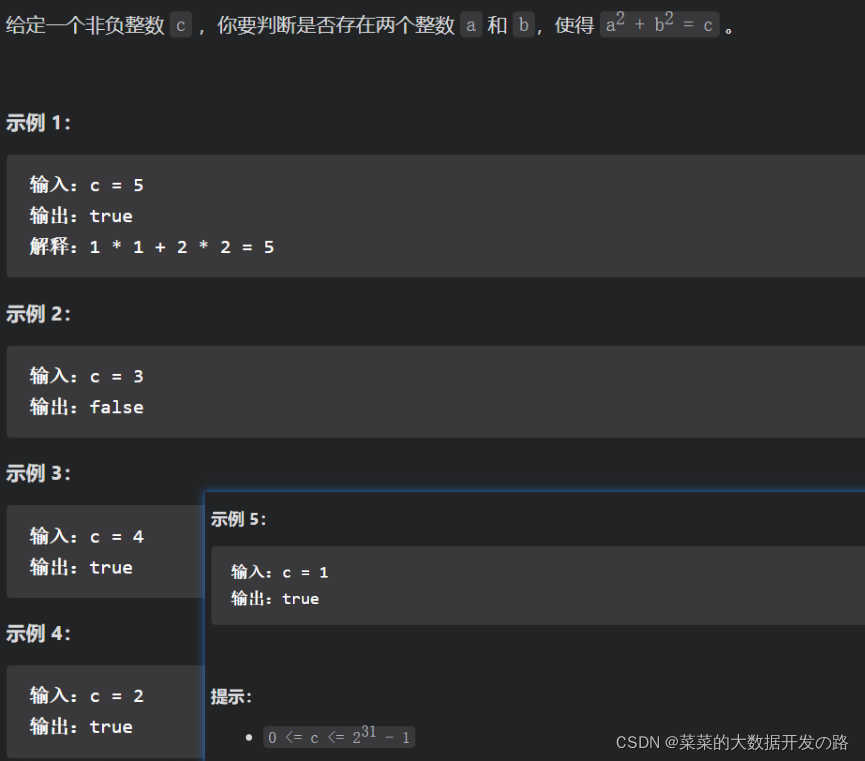
[思路分析]

[代码实现]

class Solution {
    public boolean judgeSquareSum(int c) {
        //非负整数, 0,1,2,3,4...
        //左右指针法
        long L = 0;
        long R = (long)Math.sqrt(c);

        while(L <= R){
            long res = L * L + R * R;

            if(res == c){
                return true;
            }else if(res > c){
                R--;
            }else if(res < c){
                L++;
            }
        }

        return false;
    }
}

[思路分析二, 数学法]

[代码示例]

class Solution {
    public boolean judgeSquareSum(int c) {
        for (int base = 2; base * base <= c; base++) {
            // 如果不是因子，枚举下一个
            if (c % base != 0) {
                continue;
            }

            // 计算 base 的幂
            int exp = 0;
            while (c % base == 0) {
                c /= base;
                exp++;
            }

            // 根据 Sum of two squares theorem 验证
            if (base % 4 == 3 && exp % 2 != 0) {
                return false;
            }
        }

      	// 例如 11 这样的用例，由于上面的 for 循环里 base * base <= c ，base == 11 的时候不会进入循环体
      	// 因此在退出循环以后需要再做一次判断
        return c % 4 != 3;
    }
}

lt.69-Sprt(x)

[案例需求]

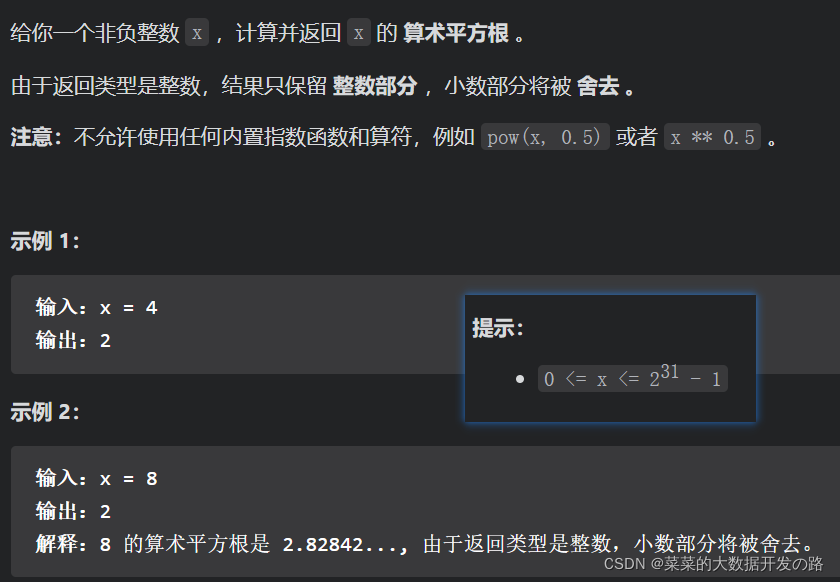
[思路分析一, 暴力法]

• 我们可以直接遍历所有可能的值, 用一个for循环, 然后不断的判断某一个i的平方是否能够等于x;

• 当然了, 如果没有一个i 正好能够等于x, 那我们就要寻找这样一个x, 他满足:

  • i 的平方 < x , 且, i + 1的平方大于x, 我们直接强制取整返回即可;

• 小小的优化: x的平方根是小于 x / 2的, 所以我们可以让i 从0到 i/ 2进行遍历, 但是0和1是不满足这个条件的, 我们单独进行判断即可;

[代码实现]

class Solution {
    public int mySqrt(int x) {
        for(long i = 0; i <= x; i++){
            if(i * i == x) return (int)i;

            if(i * i < x && (i + 1)*(i + 1) > x) return (int)i;
        }

        return -1;
    }
}

class Solution {
    public int mySqrt(int x) {

    if(x == 1)return 1;
       for(long i = 0; i <= x / 2; i++){
           if(i * i == x) return (int)i;

           if(i * i < x && (i + 1)* (i + 1) > x)return (int)i;
       }

       return -1;
    }
}

[思路分析二, 二分查找法]

[代码示例]

class Solution {
    public int mySqrt(int x) {
        int left = 0;
        int right = x / 2;

        while(left <= right){
            int mid = left + ((right - left) >> 1);

            //二分, 规定右侧是 > x, 左侧是 <= x
            if((long)mid * mid <= x){
                left = mid + 1;
            }else{ // >
                right = mid - 1;
            }
           //等到二分结束之后, right在左区间的边界, 左区间是 <= 结果的, 比如 8的平方根为2
           //而left在右区间的边界., 右区间是 > 结果的, 8的平方根会是 3
        }

        return right;
    }
}

[思路分析三, 牛顿迭代法]

• 待补充
• 题解