1.<tag-哈希表, 数组和位运算>-lt.136. 只出现一次的数字 + 137. 只出现一次的数字 II + lt.260. 只出现一次的数字 III
lt.136. 只出现一次的数字
[案例需求]
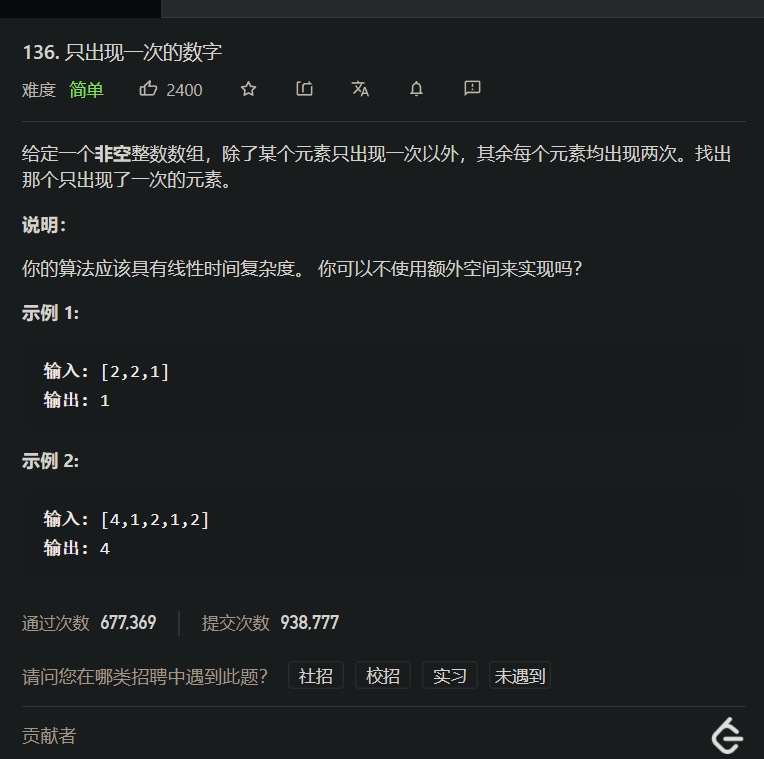
[思路分析一, 排序后遍历]
- 排序后进行遍历, 步进长度为2 (因为题目给定, 最多两个重复),
- 所以我们每次遍历的数要么是两次重复的后一个数, 要么是唯一的一个数的后面的一个数
[代码实现]
class Solution {
public int singleNumber(int[] nums) {
//暴力解法
Arrays.sort(nums);
int len = nums.length;
for(int i = 1; i < len; i += 2;){
if(nums[i] != nums[i - 1])return nums[i - 1];
}
return nums[len - 1];
}
}
# 另一种写法
class Solution {
public int singleNumber(int[] nums) {
//排序
Arrays.sort(nums);
//遍历
int i = 0;
while(i + 1 < nums.length && nums[i] == nums[i+1]){
i = i + 2;
}
return nums[i];
}
}
[思路分析三, 集合]
- 使用HashSet, 事先添加一个元素,
- 然后遍历数组和HashSet中的值进行比较(使用set.contains(x)).
- 如果发现重复(add一个值返回false, 或者说用contains方法判断), hashSet中删除这个值
- 那么遍历结束后, 根据题目中仅有一个值重复, hashset中理应当只剩下一个唯一的元素
[代码实现]
class Solution {
public int singleNumber(int[] nums) {
//哈希表
Set<Integer> set = new HashSet<>();
set.add(nums[0]);
for(int i = 1; i < nums.length; i++){
if(!set.add(nums[i])){
set.remove(nums[i]);
}else{
set.add(nums[i]);
}
}
int res = 0;
for(int x : set){
res = x;
}
return res;
}
}
[思路分析四, 哈希表]
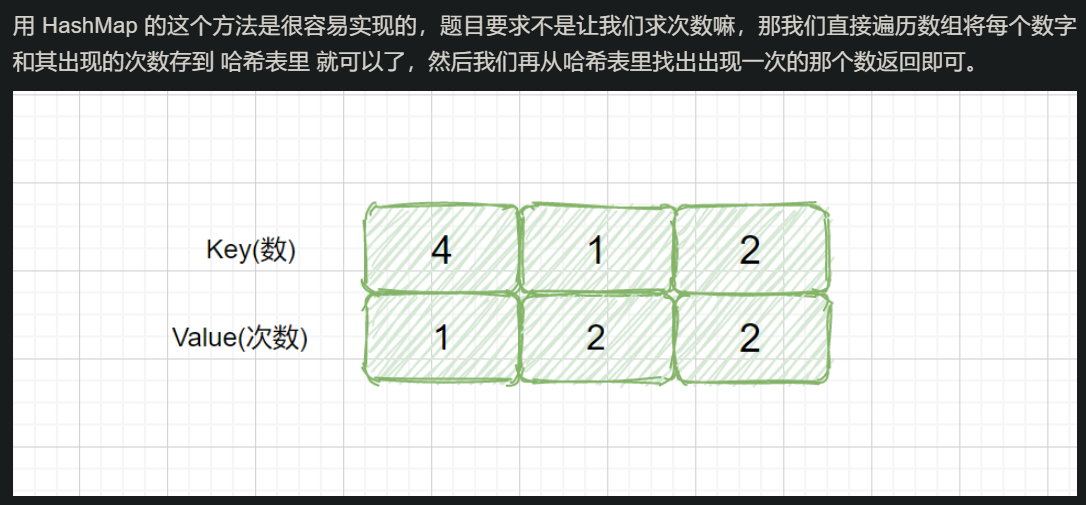
[代码实现]
class Solution {
public int singleNumber(int[] nums) {
//特殊情况
if (nums.length == 1) {
return nums[0];
}
//HashMap
HashMap<Integer,Integer> map = new HashMap<Integer,Integer>();
//将其存入哈希表中,含义为,若该元素不存在则存入表中,并计数为1,若已经存在获取次数并加1.
for (int x : nums) {
map.put(x , map.getOrDefault(x,0) + 1);
}
//遍历出出现次数为1的情况
for (int y : map.keySet()) {
if(map.get(y) == 1){
return y;
}
}
return 0;
}
}
[思路分析五, HashSet + 求和]

[代码示例]
class Solution {
public int singleNumber(int[] nums) {
if (nums.length == 1){
return nums[0];
}
HashSet<Integer> set = new HashSet<>();
int setsum = 0;
int numsum = 0;
for (int x : nums) {
//所有元素的和
numsum += x;
if (!set.contains(x)) {
//HashSet内元素的和(去重后的和, 每个元素都是唯一的)
setsum += x;
}
set.add(x);
}
//返回值
return setsum * 2 - numsum;
}
}
[思路分析五, 位运算]


异或解法:异或运算满足交换律,a^b^a=a^a^b=b,因此ans相当于nums[0]^nums[1]^nums[2]^nums[3]^nums[4]..... 然后再根据交换律把相等的合并到一块儿进行异或(结果为0),然后再与只出现过一次的元素进行异或,这样最后的结果就是,只出现过一次的元素(0^任意值=任意值)
[代码实现]
class Solution {
public int singleNumber(int[] nums) {
//注意,这里为0而不是其它值得原因并不是盲目的:甲 按位异或 0 得 甲,甲 按位异或 甲 得 0
int result = 0;
for (int i = 0; i < nums.length; i++){
// ^ 为按位异或操作符,而 ^= 相似 += ,其效果等价于 result = result ^ nums[i]
result ^= nums[i];
}
return result;
}
}
137. 只出现一次的数字 II
[案例需求]
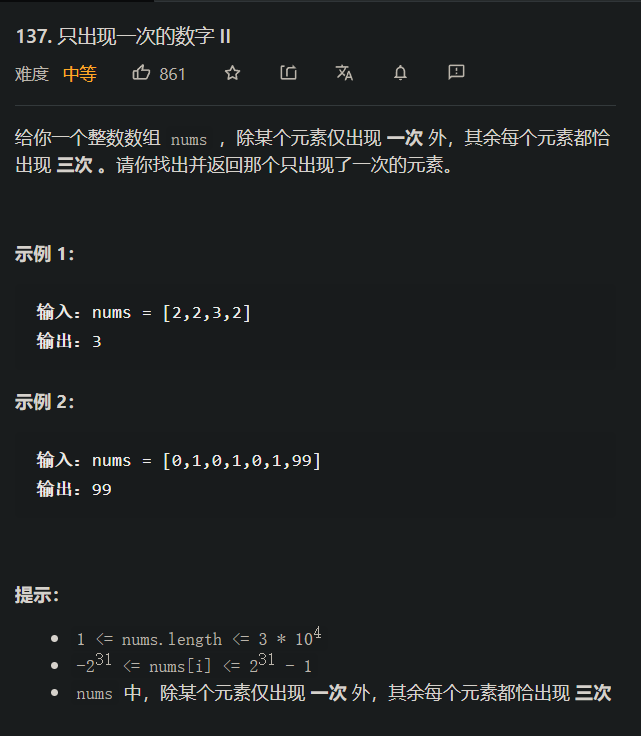
[思路分析一, 哈希表法]
[代码实现]
class Solution {
public int singleNumber(int[] nums) {
//hashMap <数, 次数>
Map<Integer, Integer> map = new HashMap<>();
for(int i = 0; i < nums.length; i++){
//
map.put(nums[i], map.getOrDefault(nums[i], 0) + 1);
}
for(int key : map.keySet()){
if(map.get(key) == 1)return key;
}
return -1;
}
}
[思路分析二, HashSet + 求和法]

[代码实现]
class Solution {
public int singleNumber(int[] nums) {
HashSet<Integer> set = new HashSet<>();
long sumset = 0;
long sumnum = 0;
for (int x : nums) {
//所有元素的和
sumnum += x;
if (set.contains(x)) {
continue;
}
//HashSet元素和
sumset += x;
set.add(x);
}
//返回只出现一次的数
return (int)((3 * sumset - sumnum) / 2);
}
}
[思路分析三, 位运算]
- 我们在第一题中有个利用异或求解的方法,但是这个题目是出现三次,我们则不能利用直接异或来求解
-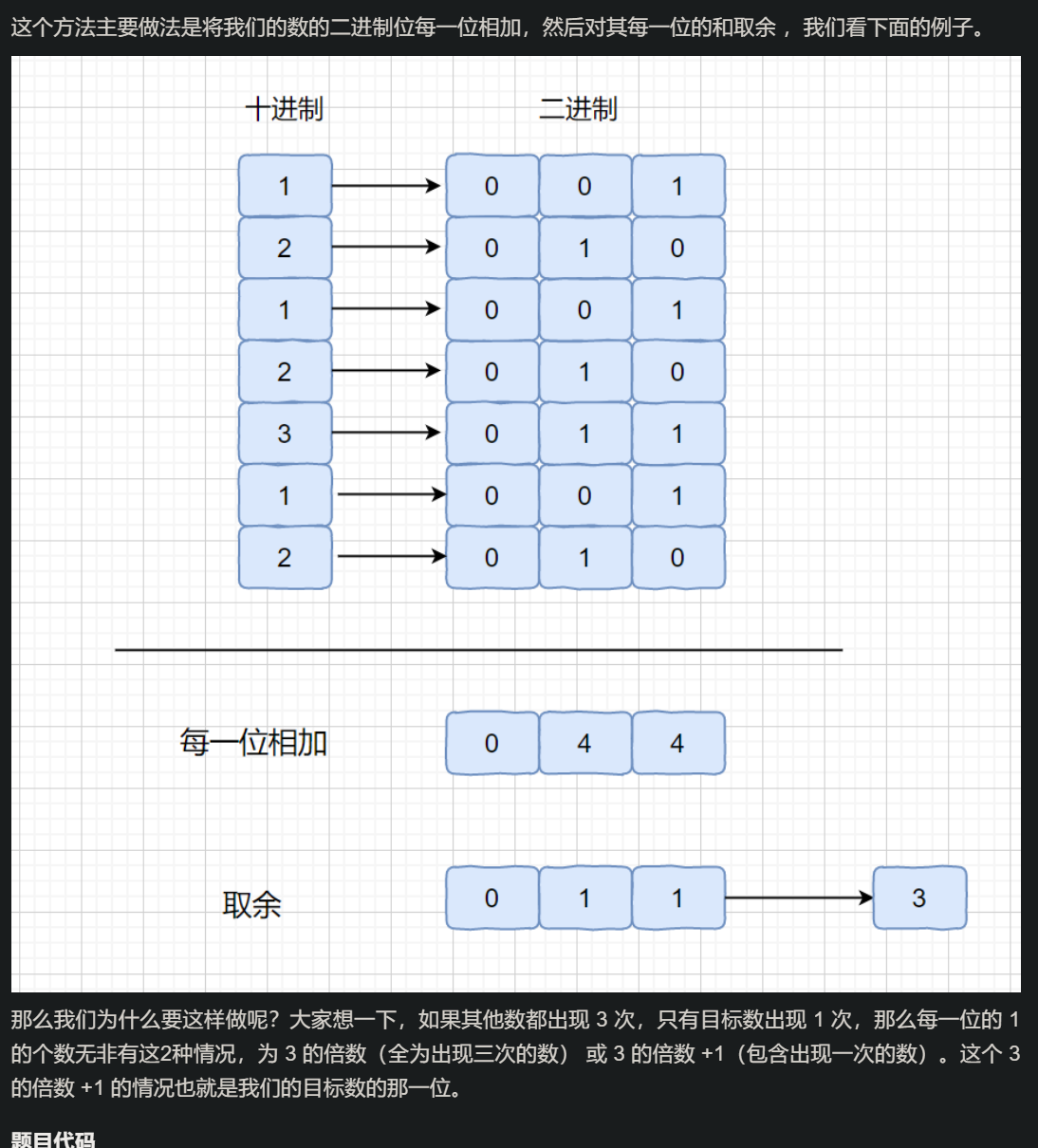
[代码示例]
class Solution {
public int singleNumber(int[] nums) {
int res = 0;
for(int i = 0; i < 32; i++){
int count = 0;
for (int j = 0; j < nums.length; j++) {
//先将数右移,并求出最后一位为 1 的个数
if ((nums[j] >> i & 1) == 1) {
count++;
}
}
//找到某一位取余为 1 的数,并左移,为了将这一位循环结束后移至原位
if (count % 3 != 0) {
res = res | 1 << i;
}
}
return res;
}
}

lt.260. 只出现一次的数字 III
[案例需求]
[思路分析一, 哈希表法]
[代码实现]
class Solution {
public int[] singleNumber(int[] nums) {
//1. 哈希表
Set<Integer> set = new HashSet<>();
set.add(nums[0]);
for(int i = 1; i < nums.length; i++){
if(!set.add(nums[i])){
set.remove(nums[i]);
}else{
set.add(nums[i]);
}
}
int[] res = new int[2];
int index = 0;
for(int x : set){
res[index++] = x;
}
return res;
}
}
[思路分析二, 位运算]

[代码实现]
class Solution {
public int[] singleNumber(int[] nums) {
int temp = 0;
//求出异或值
for (int x : nums) {
temp ^= x;
}
//保留最右边的一个 1
int group = temp & (-temp);
System.out.println(group);
int[] arr = new int[2];
for (int y : nums) {
//分组位为0的组,组内异或
if ((group & y) == 0) {
arr[0] ^= y;
//分组位为 1 的组,组内异或
} else {
arr[1] ^= y;
}
}
return arr;
}
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号