10.＜tag-二叉树和BST基础＞lt.700. 二叉搜索树中的搜索 + lt.98. 验证二叉搜索树 + lt.530. 二叉搜索树的最小绝对差(同lt.783)

lt.700. 二叉搜索树中的搜索

[案例需求]

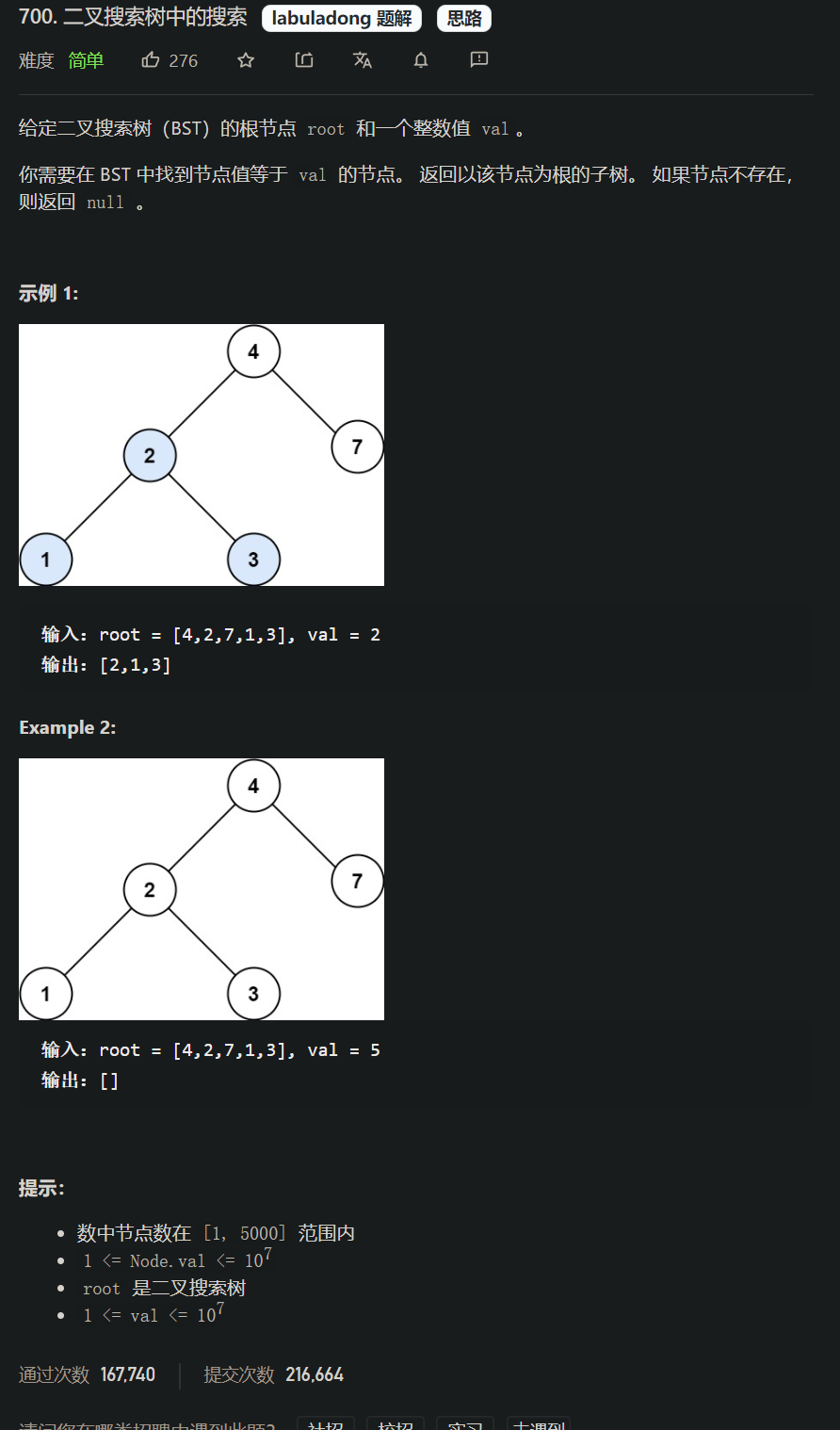
[思路分析]

• 这才是名副其实的简单题嘛
• BST: 二叉搜索树, 对于树中的每个节点,
• • 她的左节点的值都小于这个节点,
• • 她的右节点的值都大于这个节点;
    

[代码实现一, 递归法]

class Solution {
    //1. 递归函数, 查找BST, 返回值找到的节点
    public TreeNode searchBST(TreeNode root, int val) {
        //2. 递归结束条件
        if(root == null || root.val == val)return root;

        //3. 单层递归逻辑
        // if(root.val == val){
        //     return root;
        // }else 
        if(root.val > val){
            return searchBST(root.left, val);
        }else{
            return searchBST(root.right, val);
        }
    }
}

简化版

public TreeNode searchBST(TreeNode root, int val) {
    if (root == null || root.val == val) return root;
    return root.val > val ? searchBST(root.left, val) : searchBST(root.right, val);
}

[代码实现二, 迭代法]

public TreeNode searchBST(TreeNode root, int val) {
    while (root != null && root.val != val) {
        root = root.val > val ? root.left : root.right;
    }
    return root;
}

lt.98. 验证二叉搜索树

[案例需求]

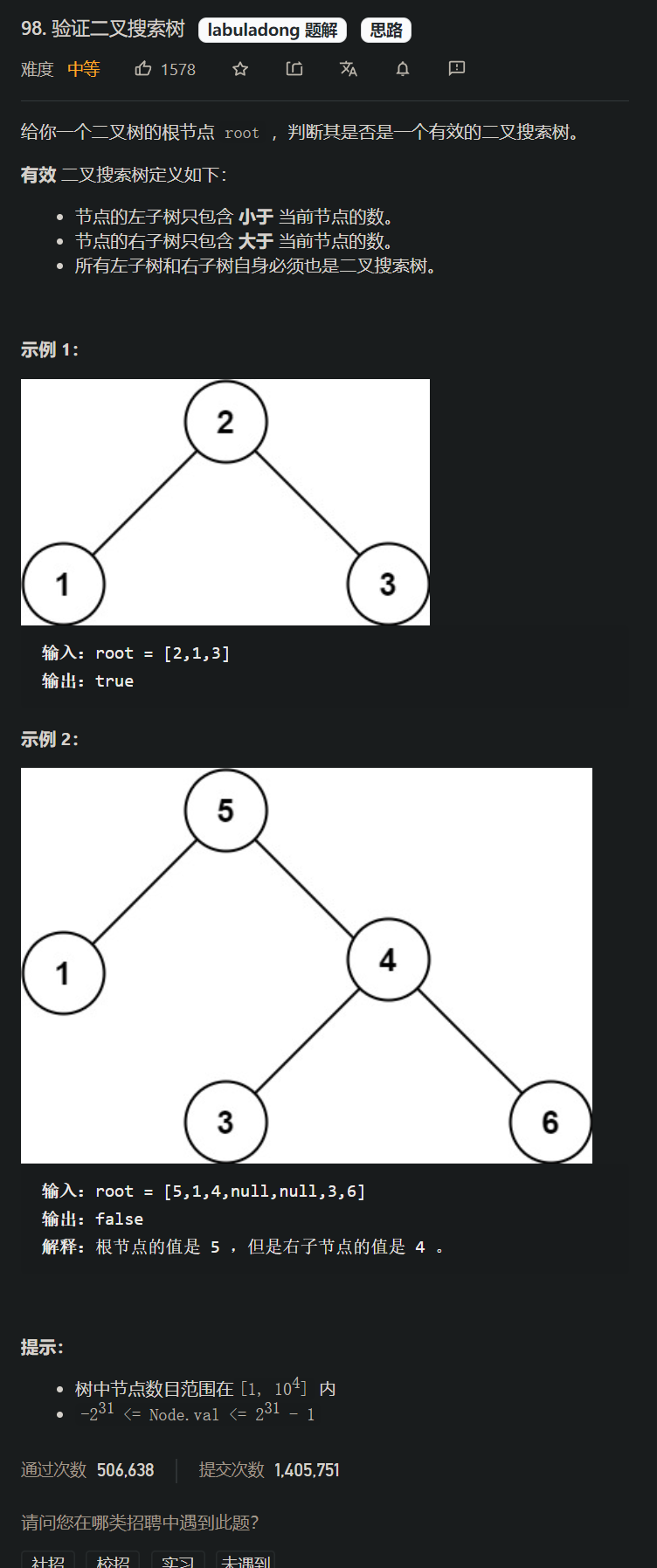
[思路分析一, 递归]

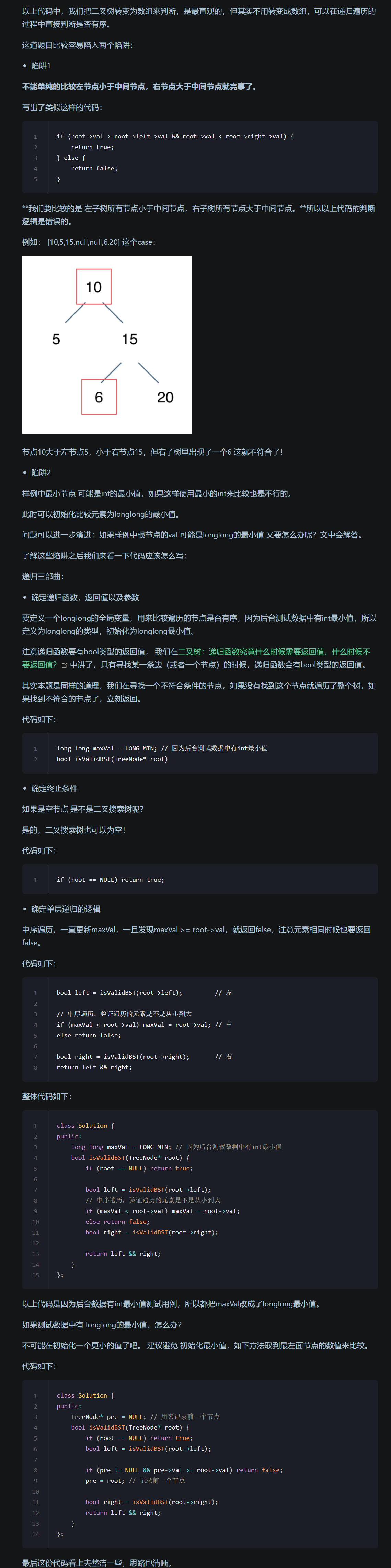
[代码实现]

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    //1. 递归函数, 验证每个节点是不是BST, 
        //参数: 被看做是根节点的当前节点
        // 返回:   时还是不是
    //long maxVal = Integer.MIN_VALUE;  ---> -long, 绝了

    TreeNode pre = null;
    public boolean isValidBST(TreeNode root) {
       //2. 递归出口
       if(root == null)return true;

       //3. 单层递归逻辑
       // BST中的中序遍历是一个递增序列
       boolean left = isValidBST(root.left); //左子树
       
       if(pre != null && pre.val >= root.val){
           return false;
       }else{
           pre = root;
       }

       boolean right = isValidBST(root.right); //右子树

       return left && right;
    }
}

[思路分析二, 集合 + 递归的方法]

• 记住这句话, 对二叉搜索树(BST)进行中序遍历, 得到的是一个升序排列的序列
• 所以我们可以对BST进行中序遍历, 一边遍历一边把遇到的数放入到集合中(因为长度未知, 不可用数组), 同时比较集合的最后一个数与将要存入的这个数是否是升序的.

[代码实现]

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    
    List<Integer> list = new ArrayList<>();

    public boolean isValidBST(TreeNode root) {
        //1. 放入集合
        return dfs(root);
    }

    public boolean dfs(TreeNode root){
        //
        if(root == null)return true;

        //单层递归逻辑
        boolean left = dfs(root.left);

        // 1. 集合不为空, 且要存入的root.val > list的最后一个元素, 升序的, 这是正确的
        if(!list.isEmpty() && list.get(list.size() - 1) < root.val){
            list.add(root.val);
        // 2. 集合不为空, 且要存入的root.val <= list的最后一个元素, 非升序的, 这是不正确的
        }else if(!list.isEmpty() && list.get(list.size() - 1) >= root.val){
            return false;
        }else{
            //3. 集合为空的时候, 直接存入元素
            list.add(root.val);
        }

        boolean right = dfs(root.right);


        return left && right;
    }
}

lt.530. 二叉搜索树的最小绝对差(同lt.783)

[案例需求]

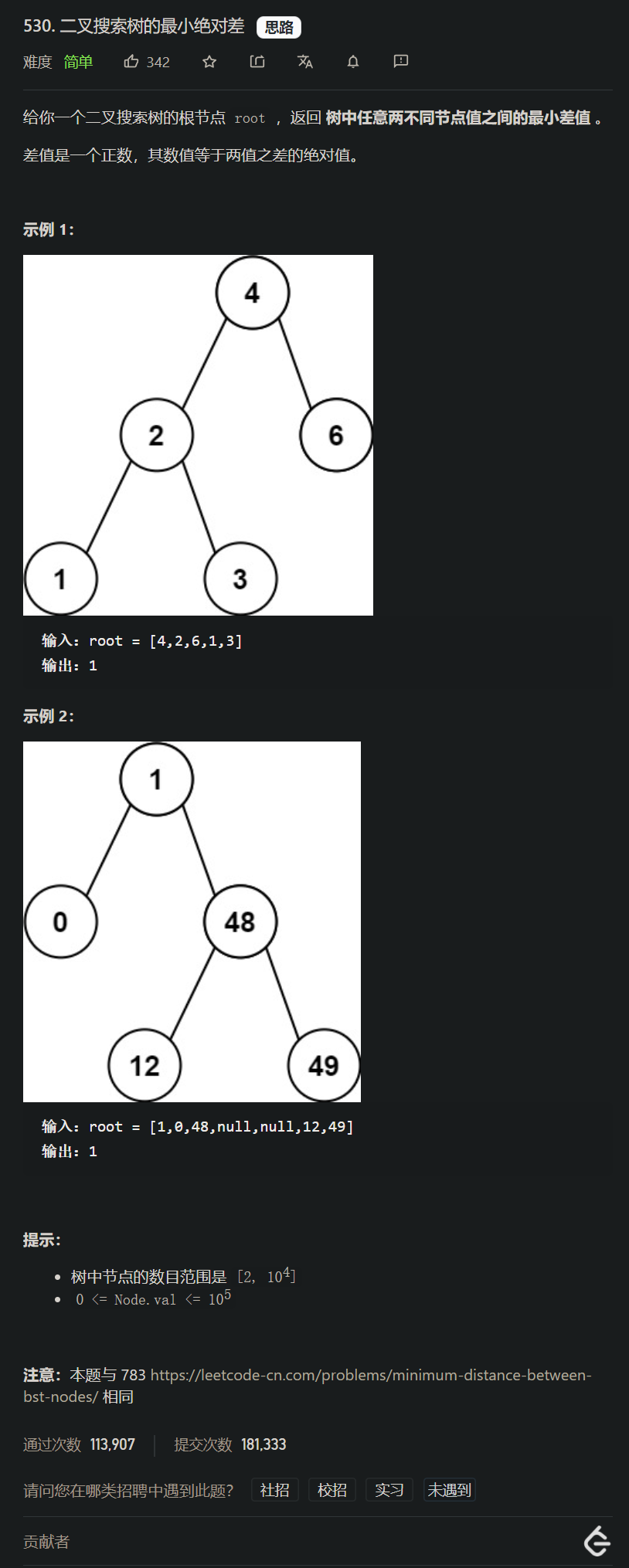
[思路分析一, 集合 + 递归]

[代码实现]

class Solution {

    List<Integer> list = new ArrayList<>();
    int res = Integer.MAX_VALUE;
    public int getMinimumDifference(TreeNode root) {
        if(root == null)return 0;

        getMinimumDifference(root.left);

        if(list.size() > 0){
            res = Math.min(res, root.val - list.get(list.size() - 1));
        }

        list.add(root.val);
        getMinimumDifference(root.right);

        return res;
    }
}

[思路分析二, 递归 + pre记录上一个遍历节点]

[代码实现]

//1.  递归 + 记录前一个节点
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    //1. 递归函数
    int res = Integer.MAX_VALUE;
    TreeNode pre = null;
    public int getMinimumDifference(TreeNode root) {
        //2. 递归出口
        if(root == null)return 0;

        //3. 单层递归逻辑(中序遍历)
        getMinimumDifference(root.left);

        if(pre != null){
            res = Math.min(res, root.val - pre.val);
        }

        pre = root;

        getMinimumDifference(root.right);

        return res;
    }
}