从头开始学习FLASH 3D教程及3D旋转轴原理
2009-09-20 10:54 宝宝合凤凰 阅读(4105) 评论(0) 收藏 举报 请看演示:
http://www.flashempire.com/school/tutorview.php?id=143 一、三维坐标系转化成二维坐标系
1、flash中的二维坐标系
(1)、坐标的转换
flash中场景左上角为(0,0),而在数学中是场景中心为(0,0),怎样把它转成数学中的坐标系呢?假设场景宽度:550,高度400。
x=550/2+this._x;//x右移
y=400/2-thix._y;//y下移
如图1。
 |
 |
|
图1:转换后的坐标系 |
图2:角度、弧度的转换 |
(2)、角度的转换
flash中角度的计算:如图2
hudu = Math.atan2(y, x);
// 利用公式tg a=y/x,计算a的值,flash中a是以
弧度表示的 ,我们要把它转换成角度,设圆的半
径r为1,整个弧长为2*pai*r,也就是说360度等于
2*pai弧度,所以转成角度的公式为:
jiaodu = hudu*180/Math.PI;
// 把弧度转换为角度,公式为:角度=弧度*180/3.14,3.14为pai
if (jiaodu<0) {
jiaodu = jiaodu+360;
}
/* 转换后的角度的范围从-180到180,
数学中的角度从0到360,所以小于0时加上360 */
2、flash中的三维坐标系
如图3,z轴表示一个物体离屏幕的远近,当物体的z轴位置增加时,物体朝远离屏幕的方向运动,当物体的z值减小时,物体朝接近屏幕的方向运动。
 |
 |
|
图3:三维坐标系 |
图4:二维与三维的点的关系 |
3、三维坐标转换成二维坐标
如图4,已知一个点(x,y,z),怎样确定该点屏幕上的位置呢?利用三角形相似的原理,可以得出下列结论:
d/(d+z)=y1/y,推出:y1=d*y/(d+z),这公式就是浪子讲的经典的算法,可在二维平面上来表现空间上的点的位置。我们还可把它进一步把它简化。提出因子d/(d+z),用ratio(比率)表示,这个公式就变为
ratio=d/(d+z);
y1=ratio*x;同理可推出
x1=ratio*y;
终于写完第一步了,休息一下,到帝国论坛下了点毛毛雨,接着我们来看第二步
二、控制物体的属性(大小,层次,透明度等)
通过第一步的学习,我们就可建立一些三维的效果,但是还有很多不足之处,如远的物体和近的物体的大小一样,层次可能也不一样,怎么办呢?
1、控制mc的大小
在三维坐标中,当z值增大,也就是远离屏幕时,物体应越小,反之越大。我们怎么在flash中表示一个mc的大小呢?还记得上一步的ratio吗?现在就要用到这东东。当z增加时,ratio减少,因为在ratio中,z是作为分母的。反之,当z减少时,ratio增加。所以可用ratio来控制mc的大小。如下:
mc1._xscale=mc._xscale*ratio;
mc1._yscale=mc._yscale*ratio;
2、控制mc的层次
z值最大,物体应在最底层,最小,在最上层,所以我们可用一个很大的常数减去z值,用此值作为mc的层次。flash中,设置mc的层次用swapDepths,如下:
mc.swapDepths(1000-z);//设置mc的层次
3、控制mc的透明度
远处的物体看上去模糊些,近处的物体清晰些,在flash中,可用_alpha来控制,方法和控制大小类似,不在介绍原理。如下:
mc._alpha=100*ratio;
4、控制mc的角度(旋转)
这一步最难,也最好的东东。学习以后,你将能制作出非常cool的效果
旋转有三种,x旋转:坐标x不变,y旋转:y不变,z旋转:z不变,我们先来推导z旋转。
如下图:从点(x,y,0)转到(x1.y1.0),求点(x1.y1.0)

利用数学中的正弦、余弦公式得出
x1=r*cos(a+b),而cos(a+b)=sina*cosb+cosa*sinb
http://www.ies.co.jp/math/java/trig/kahote/kahote.html [解释]
推出:x1=r(cosa*cosb-sina*sinb)
又因为x=r*cosa,y=r*sina
所以x1=x*cosb-y*sinb
同样推出:y1=y*cosb+x*sinb
这就是z旋转的公式。用同样的方法可推出x旋转,y旋转的公式。总结如下:
给定点:(x,y,z)
绕x轴旋转后的点(x1,y1,z1)
绕y轴旋转后的点(x2,y2,z2)
绕z轴旋转后的点(x3,y3,z3)
x旋转(x不变)
x1=x
y1=y*cosb-z*sinb
z1=z*cosb+y*sinb
y旋转(y不变)
x2=x*cosb-z1*sinb
y2=y1
z2=z1*cosb+x*sinb
z旋转(z不变)
x3=x2*cosb-y1*sinb
y3=y1*cosb+x2*sinb
z3=z2
从以上公式可看出,在flash要实现旋转,先要求x轴的旋转点,再求y轴的旋转点,最后再求出z轴的旋转点。最后我们来一个x旋转的应用
三、制作x轴旋转的正方体
1、在场景中画一小球,并按F8转换为mc,实例命名为qiu。
2、增加一层,命名为as,接下去我们来写as,如下:
_root.onLoad = function() {
shumu = 8;
// 定义复制小球的数目
qiu._x = 6000;
// 让原始小球消失
for (var i = 0; i<shumu; i++) {
duplicateMovieClip("qiu", "qiu"+i, i);
}
// 复制小球,作为正方体的八个顶点
qiu_pos_x = new Array(100, 0, 0, 100, 100, 0, 0, 100);
qiu_pos_y = new Array(100, 100, 100, 100, 0, 0, 0, 0);
qiu_pos_z = new Array(50, 50, -50, -50, 50, 50, -50, -50);
// 从三维坐标中取正方体的8个顶点的坐标,保存在数组中
D = 200;
// 观察者与屏幕的距离
hutu = 0.001;
// 控制旋转的速度
b = hutu*180/Math.PI;
// 角、弧度的转换
};
_root.onEnterFrame = function() {
for (var i = 0; i<shumu; i++) {
x1 = qiu_pos_x[i];
y1 = qiu_pos_y[i]*Math.cos(b)-qiu_pos_z[i]*Math.sin(b);
z1 = qiu_pos_z[i]*Math.cos(b)+qiu_pos_y[i]*Math.sin(b);
// 按公式计算
qiu_pos_x[i] = x1;
qiu_pos_y[i] = y1;
qiu_pos_z[i] = z1;
// 更新数组元素
ratio = D/(D+z1);
perspective_x = x1*ratio;
perspective_y = y1*ratio;
// 按公式计算
_root["qiu"+i]._x = 275+perspective_x;
_root["qiu"+i]._y = 200-perspective_y;
// 设置球的坐标
_root["qiu"+i]._xscale = _root["qiu"+i]._yscale=50*ratio;
// 球的大小
_root["qiu"+i].swapDepths(10000-qiu_pos_z[i]);
// 球的层次
_root["qiu"+i]._alpha=100*ratio;//设置透明度
}
};
3、按CTRL+Enter测试,一个简单的3D旋转就形成了。
|
http://www.7880.com/Info/Article-67a0ee40.html
大家都知道三维的点都有3个坐标,但FLASH只是有二维的坐标,所以要在FLASH里实现“三维”的效果,就需要对点的坐标进行转化,简单的说,就是怎么把三维坐标转换成二维坐标。(其实,这并不是真正的三维,而是一种视觉欺骗,看上去像三维的就这么回事。所以上面三维带引号。) 一、三维坐标系转化成二维坐标系 (1)、坐标的转换 flash中场景左上角为(0,0),而在数学中是场景中心为(0,0),怎样把它转成数学中的坐标系呢? 1.FLASH里的坐标视图 x=Stage.width/2; // Stage.width是场景的宽; y=Stage.height/2; // Stage.height是场景的高; 这样就把原坐标的原点移动了,场景的中心点,不过,Y轴还是向下,为正的。(这在后面做旋转时要注意的。)
(2)、角度的转换 flash中Math函数里的参数都要用到弧度,所以角度与弧度之间的转换是需要知道的。 在flash as中,我们可以通过这样的表达式来进行转换: hudu=jiaodu*Math.PI/180; / /把角度转换为弧度,公式为:弧度=角度 *3.14/180,3.14为pai 2、flash中的三维坐标系 如图3,z轴表示一个物体离屏幕的远近,当物体的z轴位置增加时,物体朝远离屏幕的方向运动,当物体的z值减小时,物体朝接近屏幕的方向运动。
图3:三维坐标系
图4:二维与三维的点的关系
3、三维坐标转换成二维坐标 如图4,已知一个点(x,y,z),利用三角形相似的原理,可以得出下列结论: d/(d+z)=y1/y,推出:y1=d*y/(d+z),可在二维平面上来表现空间上的点的位置。进一步把它简化。提出因子d/(d+z),用ratio(比率)表示,这个公式就变为 二、控制物体的属性(大小,层次,透明度等) 1、控制mc的大小 在三维坐标中,当z值增大,也就是远离屏幕时,物体应越小,反之越大。 我们可以用上满的ratio,当z增加时,ratio减少,因为在ratio中,z是作为分母的。反之,当z减少时,ratio增加。所以可用ratio来控制mc的大小。如下: mc1._xscale=mc._xscale*ratio; 2、控制mc的层次 z值最大,物体应在最底层,最小,在最上层, 所以mc的层次可以有z组成,可以用很大的数减z,也可以让z除以负数,等等,这里方法比较灵活,也是做”三维”效果的关键,主要要在调试中确定适合设计的方法。flash中,设置mc的层次用swapDepths,如下: mc.swapDepths(1000-z);//设置mc的层次 3、控制mc的透明度 远处的物体看上去模糊些,近处的物体清晰些,在flash中,可用_alpha来控制,方法和控制大小类似,不在介绍原理。如下: mc._alpha=100*ratio; 4、控制mc的角度(旋转) 这一步最难,也最好的东东。学习以后,你将能制作出非常cool的效果
利用数学中的正弦、余弦公式得出 x1=r*cos(a+b),而cos(a+b)=sina*cosb+cosa*sinb 这就是z旋转的公式。用同样的方法可推出x旋转,y旋转的公式。总结如下: 给定点:(x,y,z) x旋转(x不变) 注:x旋转要注意,在FLASH中x1=x y1=y*cosb+z*sinb 是先加后减,因为FLASH里的Y轴是反的,箭头向下的。 y旋转(y不变) 从以上公式可看出,在flash要实现旋转,先要求x轴的旋转点,再求y轴的旋转点,最后再求出z轴的旋转点。最后我们来一个x旋转的应用 三、制作x轴旋转的正方体 1、在场景中画一小球,并按F8转换为mc,实例命名为qiu。 2、增加一层,命名为as,接下去我们来写as,如下: _root.onLoad = function() { 3、按CTRL+Enter测试,一个简单的3D旋转就形成了。 (至此为止,上面部分的教程很大程度上是参考《flash 3D 基础教程》(作者:zjs35 文章来源:flashempire 更新时间:2004-4-7)的,本人只在上面做了微小部分的修改,主要因为这篇对FLASH_3D效果的基础理论确实写的很好。修改的部分,是本人在学习之后,自己在实践练习中发现的一些需要注意的地方。) 接下来将为大家解析一篇某人大虾写的立方体旋转的FLASH_AS,这位大虾是用纯AS写的,只要把代码全部复制到第一桢就可以了。我将做详细的解析!!! //先给各项赋值,为后面的编辑作做准备 }*/
|
|
//****************************************** //舞台上剪辑名称为_mc 经过测试可以看到: 1、rotationX 逐渐增加时 x 轴的旋转方向符合右手法则,用右手握住 x 轴,大拇指指向正方向 ,其余手指弯曲,表示旋转方向,或者是rotationX 增大的方向。 2、rotationY 逐渐增加时 y 轴的旋转方向符合右手法则,用右手握住 y 轴,大拇指指向正方向 ,其余手指弯曲,表示旋转方向,或者是rotationY 增大的方向。 3、rotationZ 逐渐增加时 z 轴的旋转方向符合右手法则,用右手握住 z 轴,大拇指指向正方向 ,其余手指弯曲,表示旋转方向,或者是rotationZ 增大的方向。 4、连续多次点击之后,具体的旋转方向已经很难说清楚了,说明 _mc 发生旋转之后,其内部的3维坐 标系也同时进行旋转,因此,rotationX、rotationY、rotationZ 都是相对于已经旋转后的坐标系而言 的,换句话来说,影片剪辑内部的旋转度数只与它自身的坐标系有关,和外部的坐标系无关。 |
http://blog.5d.cn/user12/dzxz/200812/509135.html[这里有演示]
测试代码如下:
stage.addEventListener(Event.ENTER_FRAME,onEF);
stage.addEventListener(MouseEvent.CLICK,onChg);
function onChg(evt){
k++;
}
var k:uint = 0;
function onEF(evt) {
switch ( k%3) {
case 0 :
_mc.rotationX += 5;
txt.text = "绕 X 轴旋转"
break;
case 1 :
_mc.rotationY+=5;
txt.text = "绕 Y 轴旋转"
break;
case 2 :
_mc.rotationZ+=5;
txt.text = "绕 Z 轴旋转"
break;
}
}
经过测试可以看到:
1、rotationX 逐渐增加时 x 轴的旋转方向符合右手法则,用右手握住 x 轴,大拇指指向正方向,其余手指弯曲,表示旋转方向,或者是rotationX 增大的方向。
2、rotationY 逐渐增加时 y 轴的旋转方向符合右手法则,用右手握住 y 轴,大拇指指向正方向,其余手指弯曲,表示旋转方向,或者是rotationY 增大的方向。
3、rotationZ 逐渐增加时 z 轴的旋转方向符合右手法则,用右手握住 z 轴,大拇指指向正方向,其余手指弯曲,表示旋转方向,或者是rotationZ 增大的方向。
4、连续多次点击之后,具体的旋转方向已经很难说清楚了,说明 _mc 发生旋转之后,其内部的3维坐标系也同时进行旋转,因此,rotationX、rotationY、rotationZ 都是相对于已经旋转后的坐标系而言的,换句话来说,影片剪辑内部的旋转度数只与它自身的坐标系有关,和外部的坐标系无关。
下面的例子,测试之后了解到,元件所处的层深与它的 Z 轴深度并不直接相关,但是可以根据 Z 坐标的大小进行排序,Z 值小的层深高一些,从而实现正确的层深。旋转度数也是一样,它只负责自身坐标系中的旋转,要在舞台空间中绕指定的位置进行旋转,就必须与某个角度值进行关联。相对来说,实现空间旋转更加方便了。
z 轴的深度可以自动的决定元件缩放的大小,因此这部分不需要去考虑了。
之前这个例子用 x y 坐标来计算时, x 坐标应用 cos 函数,y坐标应用sin函数,在这里发现 z 用cos ,x用sin 更准确一些,主要原因还是因为 z 的正方向是指向屏幕里面的缘故。
代码如下:
// 全局参数
var numOfBalls:Number = 5;
var radiusX:Number = 250;
var radiusY:Number = 30;
var centerX:Number = stage.stageWidth / 2;
var centerY:Number = stage.stageHeight / 2;
var speed:Number = 0.01;
var arr = new Array();
//创建对象
for (var i=1; i<=numOfBalls; i++) {
var t = this["m" + i];
t.angle = i * ((Math.PI*2)/numOfBalls);
t.addEventListener(Event.ENTER_FRAME, mover);
arr.push( t );
}
//冒泡法排序
function sortArr() {
var i,bound;
var j = arr.length - 1;
while ( j>0 ) {
bound = j;
j = 0;
for (i= 0; i<= bound -1; i++) {
if (arr[i + 1].z > arr[i].z) {
swapChildrenAt(i,i+1);
var xt = arr[i];
arr[i] = arr[i + 1];
arr[i + 1] = xt;
j = i;
}
}
}
}
//摆放对象
function mover(evt:Event) {
var t = evt.target;
t.x = Math.sin(t.angle) * radiusX + centerX;
t.y = Math.sin(t.angle) * radiusY + centerY;
t.z = Math.cos(t.angle) * radiusY * 8 + centerY;
t.rotationY = t.angle * 180/Math.PI;
//var s = t.y /(centerY+radiusY);//求出缩放比 不再需要
//t.scaleX = t.scaleY = s; 不再需要
t.angle += speed;//设置移动速度
sortArr();
}
//鼠标侦听
addEventListener(MouseEvent.MOUSE_MOVE, onMM);
function onMM(evt:MouseEvent) {
speed = ( mouseX - centerX)/3000;
}
|
//****************************************** // 全局参数 总结:
小的层深高一些,从而实现正确的层深。旋转度数也是一样,它只负责自身坐标系中的旋转,要在舞台空 间中绕指定的位置进行旋转,就必须与某个角度值进行关联。相对来说,实现空间旋转更加方便了。 z 轴的深度可以自动的决定元件缩放的大小,因此这部分不需要去考虑了。 之前这个例子用 x y 坐标来计算时, x 坐标应用 cos 函数,y坐标应用sin函数,在这里发现 z 用 cos ,x用sin 更准确一些,主要原因还是因为 z 的正方向是指向屏幕里面的缘故。 |
如果你你身边的朋友说起视角变换,2.5D,或是3D投影,可能他们在讨论这个相关的支持。
在这个小文章里,我会描述怎样来用程序熟练的操控3D空间里的元素。虽然我现在的描述看起来很复杂,但一旦你知道了怎样在Flash工作中完成视 角转换就会很简单。好了,我们就从怎样来在Flash中表现尺寸开始。
有三个坐标

这三个坐标分别用x,y,z来表示,而在你最初开始做flash时你一定是只用x,y坐标了。
利用Flash10播放器和Flash CS4,你仍可以创造和显示两个坐标轴的舞台。而现在你要做的就是依然用二维的舞台通过引起z轴来创造一个3维的场景
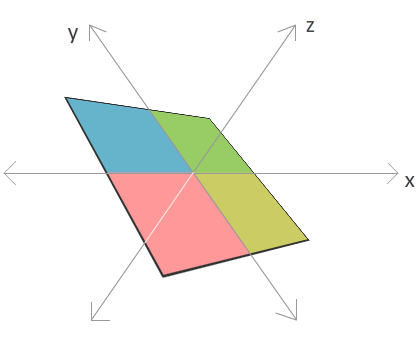
忘掉你所有与Z轴有关的东西。把它当成另外的一条你可以把你的场景放上去的直线。在这个基础上当你把X,Y轴设定好了就会看到所发生的情况。而当你把Z的值设定了之后会发生什么情况?让我们来看几个例子。
首先,看一下下面的这个图,看下当你把Z轴的值减小会发生什么。
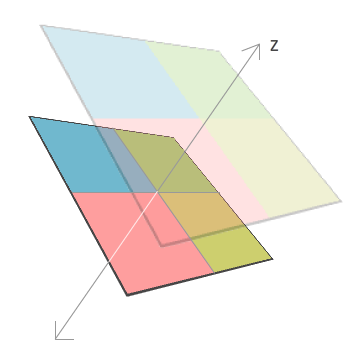
你的图形看起来变得更大。当你的Z的值增加时,情况刚好相反,你的图形看起来变得更小了。
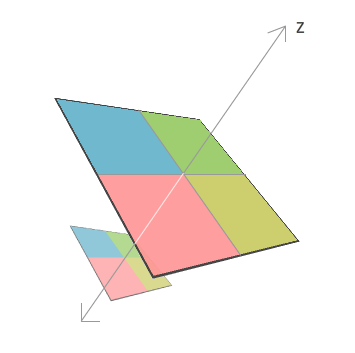
这个原因是,z的坐标一般是用来表示深度的。设想一下你在水里游泳,你潜下去多深是用Z轴的值来表示。如果你只是浮在水面上,那就相当于你的默认的深度,你的Z轴的值会是0.当你下潜的更深些的时候,你的Z轴的值就会增加。假如有人在岸上看你,就会发现,你下去的越深,你看起就会越小;而你离水面越近,你就看起来越大,代表你下潜的越浅。
在所有以上的例子中,我对X,Y,Z都简要的说明了一下以使你对这三者的关系有一个更好的理解认识。可实际上,我们总是只看到X和Y轴就像南北和东西的表示。Z轴一般是垂直于我们电脑屏幕的,所以它的方向就像有一支箭正直射你。

在大多的3D描述中,Z轴一般是用一个空心圆来表示(正如上图所示)或用一个中间有X的圆来表示。如果你要来表示方向这是很重要的。一个空心圆表示Z轴像一个箭头方向指向你。而一个中间有X的圆则表示Z轴箭头的方面刚好离你而去—这就像一支箭尾的四个羽毛正离你远去。明白了这些是不是很高兴?
下面,我们先离开下主题,看一下可以让你熟练把你场景放在3D的空间里的代码。
前面,你已经了解到各个坐标轴的作用。现在你要好好看下如何来运用Flash中的3D功能,我们来看下代码:
Looking at the Code
代码如下 :
我们从一些简单的东西开始学习。通过坐标来设定一下你元素的位置,只是设置下你实例的X,Y,Z的属性值即可:
movieClip.x = 20;
movieClip.y = 50;
movieClip.z = 100;
上面的代码使你的影片剪辑移动到(20,50)的位置,同时深度为100.换句话说,你的影片剪辑在场景的右上角,而且变小了。
另一个要完成的就是你希望这个平面可以绕任一个坐标来旋转。这个可以通过它的rotationX,rotationY, 和rotationZ三个属性来实现。
movieClip.rotationX = 180;
movieClip.rotationY = -45;
movieClip.rotationZ = 90;
下面的图来说明通过设置属性rotationX,rotationY,rotationZ会产生什么效果:
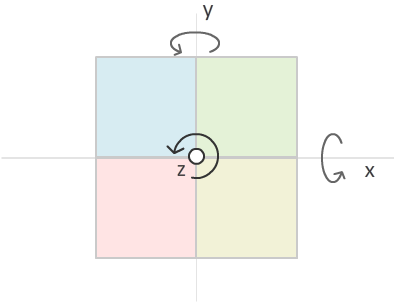
旋转有点意思。在我所描述三个坐标轴的例子里,我已经声明Z轴是垂直你的电脑屏幕的,而在我的那个游泳的例子里,我说过,Z的值相当于你在水下有多深。而当你开始旋转X,Y和Z轴的时候,现实里的图形和你在场景里看到的就会不同,当你编写3D的程序时要记着。
以上的就是了,只要设定以上我已经写出的六个属性,你就可以用以前的2D的元素来实现一些基本的3D效果。
注意的是:
尽管这些很Cool,但也有一些限制如果不借助于其它的已经存在的代码,或不用一些3D的库。
All 3D Content Gets Converted into a Bitmap
所有的3D 内容转换成位图
Flash一个3D应用的不足之处是,3D场景中,不管你创造了什么样的元素来操控,它都会自动的转变为位图。所以一旦你应用了以下任一属性:z,rotationX,rotationY,rotationZ,Flash都会把元素转换成位图。
一个完善的矢量图片,比如我一直在这里用的正方形,当你用默认的尺寸来看它时,它显示的常完美。而位图一旦你放大就会发现出现了曲带和模糊:

就论视觉而言,你可以想象来操纵一个实际的位图图片,而不仅是矢量图,它表现的也一样的完美。
相交是不可能的
当图形在3D的空间时,有趣的冲撞相碰和交叉就成为可能。不兴的是,只是这还是用编程不能实现。例如,设想你有两个平行的长方形靠的很近,如下图:
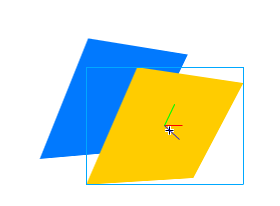
如果我要旋转蓝色的长方形,在现实里,就好像蓝色长方形的边缘部分会穿过与它临近的黄色的长方形。而实际上,发生的是好像黄色的根本不存在:
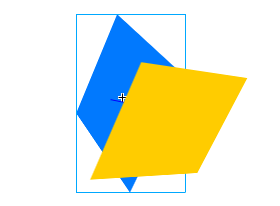
这看起来很怪谈。这好像每个元素都在各自独立的Z轴和三维空间里,而不是在一个可以相碰的空间里
Conclusion
总结:
I really hope this article helped you to understand conceptually how the x, y, and z axes are treated in Flash. The concepts are really the difficult part to fully wrap your head around. As you saw, the code itself is fairly straightforward. Even something like the example I showed on the first page is very easy to create, and I've provided the source file for that below:
//以上内容转自http://www.kirupa.com/developer/as3/intro_3d_as3_pg2.htm,并翻译过来的。如有不明白,可到网站上查看原文。






 浙公网安备 33010602011771号
浙公网安备 33010602011771号