Codeforces Round #783 (CF 1667) 简要题解

由于是 简要题解，所以只有 Div 1

CF1667A Make it Increasing

题意

给一个长度为 \(n\) 的数组 \(a\) 和一个初始全为 \(0\) 的数组 \(b\)，每次操作可以使 \(b_i\) 加上 \(a_i\) 或 \(-a_i\)，问最少几次操作可以使得 \(b\) 单调上升

\(n \le 5000\)

题解

观察样例不难发现，最终得到的 \(b\) 一定有一个位置为 \(0\)，反证法易证

枚举 \(b\) 为 \(0\) 的位置暴力计算即可，复杂度 \(O(n^2)\)

还有这破题居然卡 int

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;

const int N = 5010;

LL a[N], b[N], n, ans = 1e18;

int main()
{
    cin >> n;
    for(int i = 1; i <= n; i++) cin >> a[i];
    for(int i = 1; i <= n; i++){
        LL cur = 0, res = 0;
        for(int j = i - 1; j; j--)
            res += (cur / a[j]) + 1, cur = a[j] * ((cur / a[j]) + 1);
        cur = 0;
        for(int j = i + 1; j <= n; j++)
            res += (cur / a[j]) + 1, cur = a[j] * ((cur / a[j]) + 1);
        ans = min(ans, res);
    }
    cout << ans << endl;
    return 0;
}

CF1667B Optimal Partition

题意

给一个长度为 \(n\) 的序列 \(a\)，要求把序列划分为若干连续段，假设其中一段的长度为 \(l\)，值的和为 \(s\)，则对答案的贡献为 \(l\) 乘上 \(s\) 的符号，求最大答案

题解

考虑贪心策略

显然，对于权值和为正数的段，我们应该让他尽量长

对于权值和为负数和 \(0\) 的段，我们应该让他不出现正数（否则就一定有一种方案使得贡献更大）

也就是说，最优划分中，权值和为负数的段一定只出现负数，权值和为 \(0\) 的段一定只出现 \(0\)

那我们不妨将权值和为负数和 \(0\) 的段拆成一个一个数，容易发现这样不影响答案

发现权值和为正数的依然不好考虑，于是我们考虑 DP

设 \(f_i\) 为区间 \([1, i]\) 划分之后的最大权值和

则有

\[f_i = \max_{j = 0, s_j < s_i}^{i - 1} i - j + f_j\\ f_i = \max(f_i, f_{i - 1}), a_i = 0\\ f_i = \max(f_i, f_{i - 1} - 1), a_i < 0 \]

其中 \(s_i\) 为 \(\sum_{j = 1}^i a_j\)，即 \(a\) 的前缀和

使用平衡树或离散化+树状数组暴力转移即可，复杂度 \(O(n \log n)\)

当然，如果没有上面的分析直接暴力上树状数组也可以

代码

注：上面的分析是笔者刚刚才发现的，考场代码是树状数组暴力转移最朴素的 DP

#include <bits/stdc++.h>
#define lowbit(x) x&-x
using namespace std;
typedef long long LL;

const int N = 500010;
const int inf = 0x3f3f3f3f;

int n, t, tot, a[N], ps[N], f[N], tree1[N], tree2[N], mx[N];
LL s[N], v[N];

inline int read()
{
    int x = 0, f = 1;
    char c = getchar();
    while(c < '0' || c > '9') { if(c == '-') f = -1; c = getchar(); }
    while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
    return x * f;
}

void add(int p, int v, int *tree) { for(; p <= tot; p += lowbit(p)) tree[p] = max(tree[p], v); }
int que(int p, int *tree) { return p ? max(tree[p], que(p - (lowbit(p)), tree)) : -inf; }

int main()
{
    t = read();
    while(t--){
        n = read();
        for(int i = 1; i <= n; i++)
            a[i] = read(), s[i] = s[i - 1] + a[i], v[i] = s[i];
        sort(v, v + n + 1);
        tot = unique(v, v + n + 1) - v;
        for(int i = 0; i <= n; i++) ps[i] = lower_bound(v, v + tot, s[i]) - v + 1;

        for(int i = 1; i <= n + 1; i++) tree1[i] = tree2[i] = mx[i] = -inf;
        f[0] = mx[ps[0]] = 0, add(ps[0], 0, tree1), add(tot - ps[0] + 1, 0, tree2);
        for(int i = 1; i <= n; i++){
            f[i] = mx[ps[i]];
            f[i] = max(f[i], que(ps[i] - 1, tree1) + i);
            f[i] = max(f[i], que(tot - ps[i], tree2) - i), mx[ps[i]] = f[i];
            add(ps[i], f[i] - i, tree1), add(tot - ps[i] + 1, f[i] + i, tree2);
        }
        printf("%d\n", f[n]);

        for(int i = 0; i <= n + 1; i++)
            a[i] = ps[i] = f[i] = s[i] = v[i] = 0,
            tree1[i] = tree2[i] = mx[i] = -inf;
        n = tot = 0;
    }
    return 0;
}

CF1667C Half Queen Cover

题意

有一张 \(n \times n\) 的棋盘和一种 “半皇后” 棋子，一个 “半皇后” 可以吃和她同一行，同一列，同一条主对角线上的棋子（就是左上到右下的对角线）

问最少要多少个 “半皇后” 才能覆盖整个棋盘

要求输出方案

题解

这种构造的解题方法一般是先理论分析出一个下界再考虑构造

假设对于一个 \(n \times n\) 的棋盘，答案是 \(k\)

先考虑覆盖行和列的情况，至多有 \(k\) 行和 \(k\) 列被覆盖了，剩下 \(n - k\) 行和 \(n - k\) 列

考虑这剩下的 \(n - k\) 行和 \(n - k\) 列，不难发现，他们的元素来自 \(2n - 2k - 1\) 条不同的主对角线，而 \(k\) 个棋子最多覆盖 \(k\) 条主对角线

也就是说 \(k \ge 2n - 2k - 1\)，解不等式得 \(k \ge \frac{2n - 1}{3}\)

考虑 \(k\) 为整数的限制，不难得出一个理论下界

\[k= \left\{ \begin{array}{lc} \frac{2n-1}{3}, & n\mod 3 = 2 \\ \frac{2n}{3}, & n\mod 3 = 0 \\ \frac{2n+1}{3}, & n\mod 3 = 1 \\ \end{array} \right. \]

观察样例或者手玩一下 \(n \le 6\) 的情况，发现实际答案达到了这个下界

考虑构造

考虑贪心策略，我放的 \(k\) 个半皇后肯定是不同行，不同列，不同对角线的

而且还要满足这 \(k\) 个半皇后所占的对角线尽量靠近中间（因为这样会使得主对角线更长）

考虑分析 \(n \mod 3 = 2\) 的情况，不难想到一种可行的构造方法如下

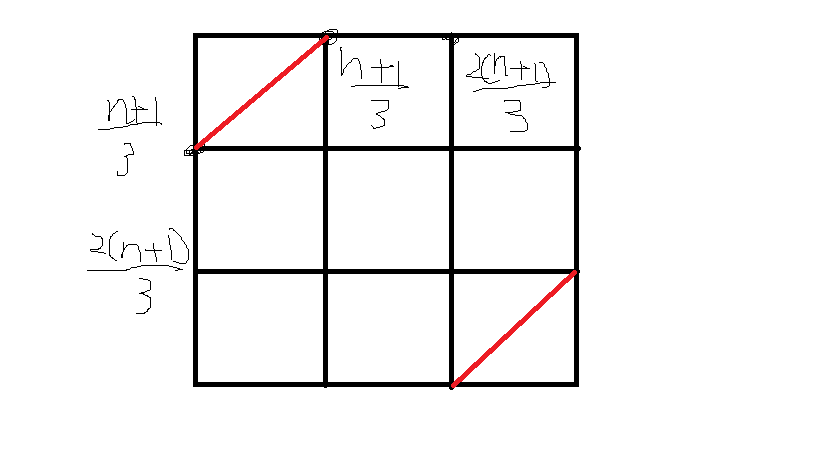
将 \(n \times n\) 的棋盘这样分成 \(9\) 部分，在左上角和右下角的部分的副对角线上放半皇后，这样完美的满足了上面的要求

其实满足上面要求的放法均是可行的（因为这样保证了覆盖的格子数）

对于 \(n + 1\) 和 \(n + 2\) 的情况，我们发现答案也分别加一和加二，于是我们只需要在右下角放上半皇后把最后的行和列覆盖掉即可

代码

#include <bits/stdc++.h>
using namespace std;

int n;

int ans(int x)
{
    if(!x) return 0;
    if(x % 3 == 2) return 2 * (x / 3) + 1;
    return ans(x - 1) + 1;
}

int main()
{
    cin >> n, cout << ans(n) << endl;
    if(n % 3 == 1) cout << n << " " << n << endl, n--;
    if(n % 3 == 0 && n) cout << n << " " << n << endl, n--;
    if(!n) return 0;

    int cur = (n / 3) + 1;
    for(int i = 1; i <= cur; i++) cout << i << " " << cur - i + 1 << endl;
    cur = cur * 2 + 1;
    for(int i = cur, j = n; i <= n; i++, j--) cout << i << " " << j << endl;
    return 0;
}

CF1667D Edge Elimination

题意

给一棵树，对于一条边，如果它两端的点度数之和是偶数，则我们可以把他删去

问能否删去所有的边，如果可以，输出方案

题解

这种构造题一般从考虑什么情况没有方案入手

不难发现一条边两端的点度数之和是偶数等价于两端点度数奇偶性相同

我们称一条边为奇边当且仅当它被删去时两端的点度数是奇数，偶边同理

考虑一个点，与他相连的边最终都要被删去，我们发现，如果一个点度数是奇数，那与他相连的边中奇边比偶边多一条，如果一个点度数是偶数，那与他相连的边中奇边与偶边数量相等

任意指定根，从叶子（即度数为一的点）向上递推，判断每个点是否满足上述性质

不难证明，如果满足上述性质，则一定存在方案，并且对于每一个点，删去与他相连的边的顺序只要满足奇偶交替即可

暴力搜索即可找到方案

代码

#include <bits/stdc++.h>
using namespace std;

const int N = 200010;
const int M = 400010;

int t, n, cnt, head[N], nxt[M], to[M], fa[N], k[N];
bool flag;

void addedge(int u, int v)
{
    to[++cnt] = v;
    nxt[cnt] = head[u], head[u] = cnt;
}

void dfs(int u)
{
    int cnt[2] = {0, 0};
    for(int i = head[u]; i; i = nxt[i])
        if(to[i] != fa[u]){
            fa[to[i]] = u;
            dfs(to[i]);
            cnt[k[to[i]]]++;
    }
    if(u > 1)
        k[u] = (cnt[0] >= cnt[1]), cnt[k[u]]++;
    if(cnt[0] > cnt[1] || cnt[1] > cnt[0] + 1) flag = 1;
}

void getans(int u)
{
    vector <int> p[2];
    for(int i = head[u]; i; i = nxt[i])
        if(to[i] == fa[u]) p[k[u]].push_back(u);
        else p[k[to[i]]].push_back(to[i]);
    int sz = p[0].size() + p[1].size(), cur = sz % 2;

    for(int i = 1; i <= sz; i++){
        int now = p[cur].back();
        if(now == u) cout << u << " " << fa[u] << endl;
        else getans(now);
        p[cur].pop_back(), cur ^= 1;
    }
}

int main()
{
    cin >> t;
    while(t--){
        cin >> n;
        for(int i = 1, u, v; i < n; i++){
            cin >> u >> v;
            addedge(u, v), addedge(v, u);
        }
        dfs(1);
        if(flag) cout << "NO" << endl;
        else{
            cout << "YES" << endl;
            getans(1);
        }

        for(int i = 1; i <= n; i++) head[i] = fa[i] = k[i] = 0;
        for(int i = 1; i <= (n << 1); i++) nxt[i] = to[i] = 0;
        n = cnt = flag = 0;
    }
    return 0;
}

CF1667E Centroid Probabilities

题意

给定奇数 \(n\)，对于每个 \(i\) 求满足如下条件的树的个数

有 \(n\) 个点
重心为 \(i\)
对于所有的 \(i \ge 2\)，与 \(i\) 相邻的点中有且仅有一个点编号比 \(i\) 小

题解

首先说明一下重心的性质

设将点 \(i\) 作为根，\(i\) 的最大子树大小是 \(t_i\)，则 \(i\) 为重心等价于 \(t_i\) 是序列 \(t\) 中最小的数

还有一个等价定义，即 \(t_i \le \frac{n}{2}\)

重心要么有一个，要么有两个。

有两个重心时，这棵树节点个数一定是偶数，并且两个重心之间有边相连。

这些性质证明较为平凡，这里不再给出。

这道题的树有一个看起来很奇怪的性质：对于所有的 \(i \ge 2\)，与 \(i\) 相邻的点中有且仅有一个点编号比 \(i\) 小。

如果你有造过树的数据，看到这个描述应该会马上反应过来，它等价于：

一棵以 \(1\) 为根的树，每个点的父节点编号均比自己小

所以对于一个节点 \(i\)，如果以 \(i\) 为根，那么 \(1\) ~ \(i - 1\) 的所有节点全部在同一棵子树内。

这也就说明了为什么 \(i > \frac{n + 1}{2}\) 时答案都是 \(0\)

所以如果 \(i\) 要是重心，那么树以 \(1\) 为根时 \(i\) 子树大小至少应该是 \(\frac{n + 1}{2}\)。

设满足 \(i\) 子树大小至少是 \(\frac{n + 1}{2}\) 的树的个数为 \(f_i\)，考虑计算 \(f\)

设 \(s = \frac{n + 1}{2}\) 我们有

\[f_i = \left\{ \begin{array}{lc} (n - 1)! & i = 1 \\ (i - 1)\sum\limits_{j = s - 1}^{n - i} \binom{n - i}{j} j! (n - j - 2)! & 2 \le i \le s \\ 0 & i \ge s + 1 \\ \end{array} \right. \]

对于 \(2\le i \le s\) 的情况，我们枚举 \(i\) 子树的大小（也就是 \(j + 1\)），将 \(j\) 个点安插在 \(i\) 子树上的方案是 \(j!\) （因为第 \(k\) 个点安放时 \(i\) 子树已经有 \(k\) 个节点了，所以父亲就有 \(k\) 种可能）

剩下 \(n - i - j\) 个点放在子树外面方案就是 \((i - 1)^{\overline{n - i - j}}\) （组合解释与上面类似），最后乘上组合数，简单化简得到上式

显然，满足上面条件的树不一定以 \(i\) 为重心，他的重心还有可能在 \(i\) 子树中

我们不妨假设整棵树以 \(i\) 为重心的方案数为 \(a_i\)

那么当 \(i\) 满足 \(i\) 子树大小至少是 \(s\) 但是重心是 \(j(j>i)\) 时，这样的情况有 \(\frac{a_j}{i}\) 种

因为放第 \(j\) 个点时，它到 \(1\) 的路径上经过 \(i\) 的概率是 \(\frac{1}{i}\) （这个结论对 \(j\) 用数学归纳法容易得到，这里不再证明）

所以，我们有递推式

\[a_i = f_i - \sum_{j = i + 1}^{n} a_j \]

如果我们从后往前枚举 \(i\)，后面的和式就可以用后缀和计算

考虑如何计算 \(f_i\)，显然我们主要考虑 \(2 \le i \le s\) 的部分，即

\[\begin{equation} \begin{split} f_i &= (i - 1)\sum_{j = s - 1}^{n - i} \binom{n - i}{j} j! (n - j - 2)! \\ &= (n - i)!(i - 1)\sum_{j = s - 1}^{n - i} \frac{(n - j - 2)!}{(n - i - j)!}\\ &= (n - i)!(i - 1)! \sum_{j = s - 1}^{n - i} \binom{n - j - 2}{i - 2}\\ &= (n - 1)!(i - 1)! \sum_{j = i - 2}^{n - s - 1} \binom{j}{i - 2}\\ &= (n - 1)!(i - 1)!\binom{n - s}{i - 1}\\ \end{split} \end{equation} \]

预处理阶乘及其逆元，暴力递推即可做到 \(O(n)\)

有点搞不懂 std 为什么要用 NTT

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;

const int N = 200010;
const LL p = 998244353;

LL n, s, tmp, f[N], ans[N], fac[N], inv[N];

LL ksm(LL v, LL tms)
{
    LL res = 1;
    for(; tms; tms >>= 1, v = v * v % p) if(tms & 1) res = res * v % p;
    return res;
}

void pre(int mx)
{
    fac[0] = inv[0] = 1;
    for(int i = 1; i <= mx; i++) fac[i] = fac[i - 1] * i % p;
    inv[mx] = ksm(fac[mx], p - 2);
    for(int i = mx - 1; i; i--) inv[i] = inv[i + 1] * (i + 1) % p;
}

LL c(LL n, LL m)
{
    if(n < m || m < 0) return 0;
    return fac[n] * inv[m] % p * inv[n - m] % p;
}

LL getinv(int x) { return inv[x] * fac[x - 1] % p; }

int main()
{
    cin >> n, s = (n + 1) >> 1;
    pre(n + 1);
    f[1] = fac[n - 1];
    for(int i = s + 1; i <= n; i++) f[i] = 0;
    for(int i = 2; i <= s; i++)
        f[i] = fac[n - i] * fac[i - 1] % p * c(n - s, i - 1) % p;

    for(int i = n; i >= 1; i--){
        ans[i] = (f[i] - tmp * getinv(i) % p + p) % p;
        tmp = (tmp + ans[i]) % p;
    }
    for(int i = 1; i <= n; i++) cout << ans[i] << " ";
    puts("");
    return 0;
}

CF1667F Yin Yang

暂时不会

update: 这题什么玩意，放弃了

posted @ 2022-04-30 21:19 sgweo8ys 阅读(180) 评论(0) 收藏举报

刷新页面返回顶部

sgweo8ys