Codeforces Round #779 (CF1658) 简要题解
CF1658A Marin and Photoshoot
题意
给一个 01 序列,如果要使其中任何一个长度大于等于 \(2\) 的子段都满足 \(1\) 的个数不少于 \(0\) 的个数,问至少要在其中插入几个 \(1\)
题解
不难发现,如果长度为 \(2\) 和 \(3\) 的子段都满足,那么其他的肯定也都满足(因为他们可以表示成长度为 \(2\) 和 \(3\) 的子段的拼接)
长度为 \(2\) 和 \(3\) 的子段不满足条件的有 \(00\),\(001\),\(100\),\(010\)
显然,长度为 \(2\) 和 \(3\) 的子段满足条件等价于相邻两个 \(0\) 之间隔了至少两个 \(1\)
暴力枚举即可,复杂度 \(O(n)\)
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 110;
int t, n;
char s[N];
int main()
{
scanf("%d", &t);
while(t--){
scanf("%d", &n);
scanf("%s", s + 1);
int ans = 0, lst = 0;
for(int i = 1; i <= n; i++){
if(s[i] == '0'){
if(lst) ans += max(0, 3 - i + lst);
lst = i;
}
}
printf("%d\n", ans);
}
return 0;
}
CF1658B Marin and Anti-coprime Permutation
题意
给定 \(n\),求长度为 \(n\) 的排列 \(p\) 的个数
其中 \(p\) 要满足 \(\gcd(p_1 \times 1, p_2 \times 2, ... ,p_n \times n) > 1\)
题解
设 \(w_p = \gcd(p_1 \times 1, p_2 \times 2, ... ,p_n \times n)\)
如果 \(w_p > 1\) 则其一定有至少一个质因子,不妨假设其中一个为 \(a\)
\(1\) 到 \(n\) 中,是 \(a\) 的倍数的数有 \(\lfloor \frac{n}{a} \rfloor\) 个
显然一个 \(1\) 到 \(n\) 的排列也是这么多,所以总共就是 \(2 \times \lfloor \frac{n}{a} \rfloor\)
那么因为 \(w_p\) 是 \(\gcd\),所以对于所有的 \(i, p_i \times i\) 一定有 \(a\) 这个质因子
那也就是说 \(2 \times \lfloor \frac{n}{a} \rfloor \ge n\),显然 \(a\) 只能是 \(2\),并且 \(n\) 也只能是偶数
并且对于任意的奇数 \(i\),\(p_i\) 都是偶数,对于任意的偶数 \(j\),\(p_j\) 都是奇数
所以答案就是 \(1\) 到 \(n\) 中偶数的全排列乘上奇数的全排列
也就是
暴力计算即可
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1010;
const LL p = 998244353;
LL fac[N];
void pre(int mx)
{
fac[0] = 1;
for(int i = 1; i <= mx; i++) fac[i] = fac[i - 1] * i % p;
}
int main()
{
pre(1000);
int t;
cin >> t;
while(t--){
int n;
cin >> n;
cout << ((n & 1) ? 0 : fac[n >> 1] * fac[n >> 1] % p) << endl;
}
return 0;
}
CF1658C Shinju and the Lost Permutation
题意
有一个长度为 \(n\) 的排列,已知它循环移位 \(i\) 位后前缀最大值个数是 \(c_i\),问这样的排列是否存在
题解
首先,前缀最大值有一个当且仅当 \(n\) 在第一位,所以 \(c\) 中有且仅有一个 \(1\)
然后,对于一次循环移位,会将第 \(n\) 位的值移到第 \(1\) 位,这样它一定是前缀最大值(因为长度为 \(1\) 的前缀就它一个值),也就是说,前缀最大值的个数会加 \(1\)
接着,我们发现第 \(n\) 位的值移到第 \(1\) 位后,它会使后面的一些前缀最大值变得不是最大值,也就是说,前缀最大值的个数会减少一些
所以,一定有 \(c_i + 1 \ge c_{i+1}\)
最后,别忘了,还要满足 \(c_n + 1 \ge c_1\) (因为这是循环移位)
观察发现,满足上面的条件的 \(c\) 数组一定是可行的
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
int a[N], t, n;
void solve()
{
int cnt = 0, pos = 0;
for(int i = 1; i <= n; i++)
if(a[i] == 1) cnt++, pos = i;
if(cnt != 1) return puts("NO"), void();
for(int i = 1; i <= n; i++){
int nxt = ((i == n) ? 1 : i + 1);
if(a[nxt] - a[i] > 1) return puts("NO"), void();
}
puts("YES");
}
int main()
{
cin >> t;
while(t--){
cin >> n;
for(int i = 1; i <= n; i++) cin >> a[i];
solve();
}
return 0;
}
CF1658D2 388535 (Hard Version)
题意
给定 \(l,r\) 和一个长度为 \(r - l + 1\) 的整数数组 \(a\),求一个整数 \(x\) 满足存在一个 \(l\) 到 \(r\) 的排列 \(p\) 使得 \(p_i \oplus x = a_i\)
保证有解
题解
std1
非常神奇的解法
考虑不知道为什么就突然想到的一个事实
也就是说,如果初始时 \(a \oplus b = 1\),那么异或上 \(x\) 之后,他们的异或和还是 \(1\)
那我们将 \(l\) 到 \(r\) 中异或和为 \(1\) 的两两配对,再将 \(a\) 中的异或和为 \(1\) 的数两两配对,会出现以下几种情况
-
\(l\) 是偶数,\(r\) 也是偶数, \(r\) 无法配对
- 那么 \(a\) 中必然也剩下一个无法配对的元素 \(a_i\),他和 \(r\) 的异或和一定就是 \(x\) (因为 \(r \oplus x = a_i\))
-
\(l\) 是奇数,\(r\) 也是奇数, \(l\) 无法配对
- 与第一种情况类似
-
\(l\) 是奇数,\(r\) 是偶数,\(l\) 和 \(r\) 都无法配对
- 那么 \(a\) 中必然也剩下两个无法配对的元素,他们和 \(l, r\) 也就两种对应的可能,枚举判断即可
-
\(l\) 是偶数,\(r\) 是奇数,全都配对了
-
不难发现另一个事实: \(a \oplus b = 2 \Rightarrow (a \oplus x) \oplus (b \oplus x) = 2\),
-
令 \(x\) 二进制下 \(2^0\) 那一位为 \(0\)(当然 \(1\) 也可以),将 \(l\) 到 \(r\) 和 \(a\) 中的所有元素全部右移一位(并去重),递归即可
-
std2
不难发现 \(p_i \oplus x = a_i\) 也就是 \(a_i \oplus x = p_i\)
因为保证有解,所以 \(a_i\) 肯定互不相同,所以只需要满足 \(l \le a_i \oplus x \le r\) 即可
不难想到对 \(a\) 数组建 01 trie
枚举每个可能的 \(x\) (\(l \oplus a_i\)),用 01 trie 贪心求出最大最小异或和并判断即可
我的考场暴力
不难发现 \(p_i \oplus x = a_i\) 也就是 \(a_i \oplus x = p_i\)
因为保证有解,所以 \(a_i\) 肯定互不相同,所以只需要满足 \(l \le a_i \oplus x \le r\) 即可
由于我很菜,所以没想到对 \(a\) 数组建 01 trie
考虑在二进制上从大到小枚举每一位
假设枚举到第 \(i\) 位,这一位上 \(l\) 到 \(r\) 共有 \(x\) 个 \(1\) 和 \(y\) 个 \(0\)
显然,由于保证有解,所以 \(a\) 数组一定有 \(x\) 个 \(1\) 和 \(y\) 个 \(0\) 或 \(x\) 个 \(0\) 和 \(y\) 个 \(1\)
如果 \(x \neq y\),那可以判断出 \(x\) 这一位是 \(0\) 还是 \(1\)
否则,是 \(0\) 是 \(1\) 还不好说
考虑爆搜,复杂度 \(O(n^2)\)
考虑剪枝,如果异或到第 \(i\) 位时最大值已经大于 \(r\),显然不行,如果最小值加上 \(2^i - 1\)(假设后面都是 \(1\)) 都小于 \(l\),显然也不行
复杂度依然是 \(O(n^2)\)
数据范围 \(n \le 2^{17}(\approx 1.3 \times 10^5)\)
实际用时 499ms
代码(std1)
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 5;
int a[N], l, r;
set <int> s, s2;
void solve() {
int mul = 1;
s.clear();
cin >> l >> r;
for (int i = l; i <= r; ++i) {
cin >> a[i];
s.insert(a[i]);
}
for (; l % 2 == 0 && r % 2 == 1; l >>= 1, r >>= 1, mul <<= 1) {
s2.clear();
for (int i: s) s2.insert(i >> 1);
swap(s, s2);
}
int ans;
if (l % 2 == 0) ans = r;
else ans = l;
for (int i: s) {
if (s.find(i ^ 1) == s.end()) {
int cur = i ^ ans;
bool f = true;
for (int j : s)
f &= ((cur ^ j) >= l && (cur ^ j) <= r);
if (f) {
ans = cur;
break;
}
}
}
cout << ans * mul << '\n';
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int t; cin >> t;
while (t--) solve();
return 0;
}
CF1658E Gojou and Matrix Game
题意
有一个 \(n \times n\) 的矩阵 \(v\),其中 \(v_{i, j} < n^2\) 且互不相等,G 和 M 两人轮流取数,每个数可以被取多次,但取的位置与上一个人取的位置的曼哈顿距离不能小于等于 \(k\),M 先取,对于每个 \((i, j)\) 输出如果 M 第一步取 \(v_{i,j}\),在选了好多好多步之后会是谁赢
题解
std
不会 English,看不懂
感觉比我的解法简单很多啊
update: 看懂了,跟我的解法差不多,只是它把 sg 用 dp 描述了
我的解法
显然,一个人选了数之后,下一个人不会选比他更小的(否则第一个人可以继续选那个数)
所以我们可以强制让每个人只选比上一个人选的数更大的数
这样就有一个很好的性质:不能行动者输
也就是说,这是个公平组合游戏
考虑算出 sg 函数
这里我们不需要准确知道 sg 值是多少,我们只需要知道他是不是 \(0\) 就行
显然我们要按照每个点上的数字从大到小对点排序,然后依次考虑每个点的 sg 值
假设现在考虑到了第 \(i\) 个点
那它的后继状态就是 \(1\) 到 \(i-1\) 中与 \(i\) 的曼哈顿距离大于 \(k\) 的点
如果这些点有一个 sg 为 \(0\),那第 \(i\) 个点就不是 \(0\)
否则它就是 \(0\)
那如何考虑曼哈顿距离呢
如图:
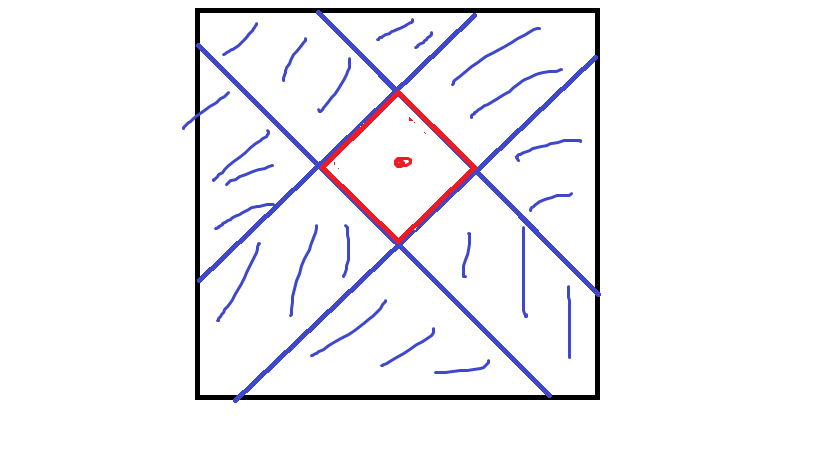
对于红色的点,与他曼哈顿距离小于等于 \(k\) 的点在红色框内,红色框是一个小正方形,且每条边与矩阵的边夹角都为 \(45\) 度
大于 \(k\) 的自然就是蓝色阴影部分
由于我们要判断大于 \(k\) 的区域内有没有 \(0\),这显然是个可重复贡献问题,于是我们把蓝色阴影拆成四个三角形
如图(上一张图的痕迹擦不干净了):
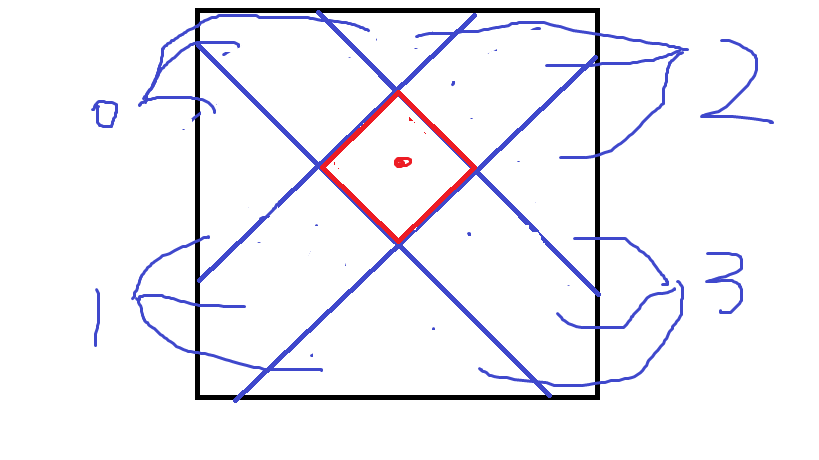
也就是红色框四条边延长线与矩阵边界所围成的三角形
对于一个三角形,考虑这样分析
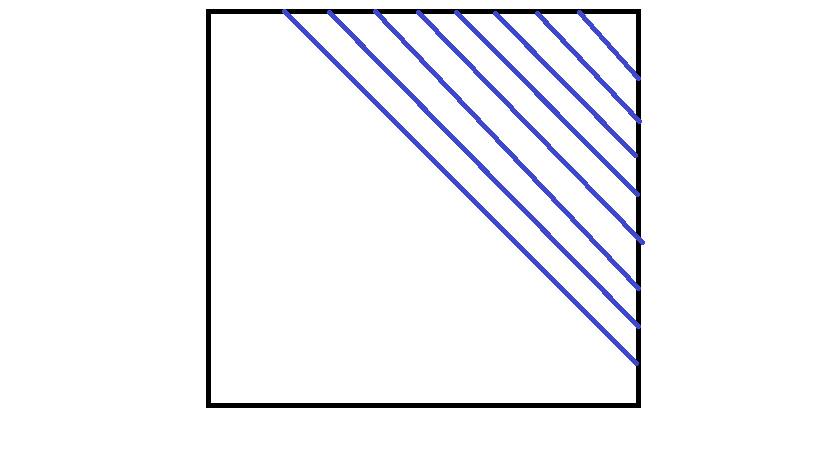
一个如图的三角形内没有 \(0\) 等价于它的它的斜边的右上方的斜边(包括它自己)没有 \(0\)
维护一个最右上的出现 \(0\) 的斜边即可
其他三个三角形类似
复杂度 \(O(n^2)\) (如果使用基数排序的话)
代码(我的解法)
注:未使用基数排序,复杂度为 \(O(n^2 \log n)\)
还要注意一下,sg 为 \(0\) 说明面对这种情况的人无法行动,也就是创造这种情况的人赢了,所以这里 sg 为 \(0\) 是说 M 选了一个数使得 G 需要面对一个 sg 为 \(0\) 的情况,也就是 M 赢了
#include <bits/stdc++.h>
using namespace std;
const int N = 2010;
const int inf = 0x3f3f3f3f;
struct node{
int x, y, v;
bool operator <(const node a)const{
return v > a.v;
}
}a[N * N];
int n, k, m, pro[4];
char ans[N][N];
inline int read()
{
int x = 0, f = 1;
char c = getchar();
while(c < '0' || c > '9') { if(c == '-') f = -1; c = getchar(); }
while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
return x * f;
}
int main()
{
n = read(), k = read(), m = n * n;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
a[(i - 1) * n + j] = (node){i, j, read()};
sort(a + 1, a + m + 1);
pro[0] = pro[2] = inf, pro[1] = pro[3] = -inf;
for(int i = 1; i <= m; i++){
int x = a[i].x, y = a[i].y, res = 1;
if(x - k - 1 + y >= pro[0]) res = 0;
else if(x + k + 1 - y <= pro[1]) res = 0;
else if(x - k - 1 - y >= pro[2]) res = 0;
else if(x + k + 1 + y <= pro[3]) res = 0;
if(res) ans[x][y] = 'M';// res = 1 说明 sg 是 0 ,赢的就是 M
else ans[x][y] = 'G';
if(res){
pro[0] = min(pro[0], x + y), pro[1] = max(pro[1], x - y);
pro[2] = min(pro[2], x - y), pro[3] = max(pro[3], x + y);
}
}
for(int i = 1; i <= n; i++){
for(int j = 1; j <= n; j++) putchar(ans[i][j]);
putchar('\n');
}
return 0;
}
CF1658F Juju and Binary String
题意
给定一个长度为 \(n(n\le 2\times 10^5)\) 的 01 序列,你需要在其中找出长度和为 \(m\) 若干个不相交子段,使得这些子段的 \(1\) 的个数与子段长度和之比等于原序列中 \(1\) 的个数与 \(n\) 的比
现在要求最小化找出的子段的个数,并输出其中一种方案,若无可行方案输出 \(-1\)
题解
很神奇的一道题
下面称 “一段序列中 \(1\) 的个数与序列长度的比值” 为 “一段序列中 \(1\) 的占比”
首先,这道题很容易被误解成“找出长度和为 \(m\) 若干个不相交子段,使得这些子段的 \(1\) 的个数为 \(k\)”,因为我们显然可以算出我们要找的子段中一共有几个 \(1\)
然后上面那个问题看着就很像 wqs 二分优化 dp 或者是二分答案(然后我就对着这个问题想了好久
但我们显然可以发现,原题其实是一种特殊情况,我们不妨考虑一下他对比上面的问题特殊在哪
原题中,原序列和我们要找的子段中 \(1\) 的占比是一样的
然后我们发现,对于长度均为 \(m\) 的两个子段 \([l, r]\) 和 \([l+1, r+1]\),他们之间 \(1\) 的数量变化是连续的(也就是说 \(1\) 的个数最多增加 \(1\),也最多减少 \(1\))
那如果我们能找到若干个长度均为 \(m\) 的子段(允许相交),使得他们拼在一起(重复部分算多次)之后 \(1\) 的占比为 \(p\),那就一定存在一个长度为 \(m\) 的子段满足其中 \(1\) 的占比为 \(p\)
当然,前提是 \(m \times p\) 是整数
简单的证明:
- 若我们找的长度为 \(m\) 的子段中存在一段满足 \(1\) 的占比为 \(p\),那结论显然成立
- 若不存在,则
- 考虑占比最小的一段 \([l_1, r_1]\),它当中 \(1\) 的占比一定小于 \(p\),同理,最大的一段 \([l_2, r_2]\) 中 \(1\) 的占比一定大于 \(p\)(否则所有段加起来不可能等于 \(p\))
- 也就是说,\([l_1, r_1]\) 中 \(1\) 的个数小于 \(m \times p\),\([l_2, r_2]\) 中 \(1\) 的个数大于 \(m \times p\)
- 由于 \(1\) 的个数在相邻两个长度相等的子段上呈连续变化,左端点在 \((l_1, l_2)\) 之间的长度为 \(m\) 的子段中一定会存在一段满足 \(1\) 的个数为 \(m \times p\)
再回顾另一个条件:
他们拼在一起(重复部分算多次)之后 \(1\) 的占比为 \(p\)
再回顾一下前面提到的原题的特殊之处:
原序列和我们要找的子段中 \(1\) 的占比是一样的
惊人的相似,直觉告诉我们这绝对不是巧合
如果我们将原序列考虑成循环序列,也就是 \(n\) 的后一位是 \(1\),那我们将会发现一个惊人的事实:
以每个点为左端点,长度为 \(m\) 的子段刚好覆盖了原序列 \(m\) 次,也就是说他们拼在一起得到了我们想要的占比
也就是说,如果原序列真的是循环序列,那答案就是 \(1\)
可惜它不是
但我们马上发现,就算不是循环序列,答案也不会超过 \(2\)
证明:
刚刚我们已经说过,如果原序列是循环序列,答案就是 \(1\)
找到那个答案(有多个的话选左端点最靠左的),设为 \([l, r]\)
如果 \(l \le r\),也就是说即使不需要循环他也是答案,那么最小子段个数就是 \(1\)
否则,最小子段个数就是 \(2\),即为 \([1, r]\) 和 \([l, n]\)
模拟即可,复杂度 \(O(n)\)
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 200010;
int t, n, m, a[N];
void solve()
{
int cnt = 0, tar, l = 1, r = m, cur = 0;
for(int i = 1; i <= n; i++) cnt += a[i];
if(1ll * cnt * m % n != 0) return puts("-1"), void();
tar = 1ll * cnt * m / n;
for(int i = 1; i <= m; i++) cur += a[i];
for(; l <= n; l++, r = ((r == n) ? 1 : r + 1), cur += a[r]){
if(cur == tar){
if(r >= l) printf("1\n%d %d\n", l, r);
else printf("2\n%d %d\n%d %d\n", 1, r, l, n);
return ;
}
cur -= a[l];
}
}
int main()
{
cin >> t;
while(t--){
cin >> n >> m, getchar();
for(int i = 1; i <= n; i++) a[i] = getchar() - '0';
solve();
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号