Codeforces Round #777 (CF1647) 简要题解
CF1647A Madoka and Math Dad
题意
求不含 \(0\),相邻的位数字不相等,各位数字之和等于 \(n\) 的最大整数,\(n \le 1000\)
题解
观察样例不难发现,答案的数字只由 \(1\) 和 \(2\) 组成,因为如果存在其他数,将其拆成 \(1\) 和 \(2\) 显然可以扩大答案
那么答案要么是 \(1212121...\),要么是 \(2121212...\)
发现可以按 \(n \mod 3\) 分类
如果 \(n \mod 3 = 0 or 2\),答案就是 \(2121212..\),如果 \(n \mod 3 = 1\),答案就是 \(1212121...\)
代码
#include <bits/stdc++.h>
using namespace std;
int t, n, cur;
int main()
{
cin >> t;
while(t--){
cin >> n;
if(n % 3 == 0 || n % 3 == 2) cur = 2;
else cur = 1;
while(n){
printf("%d", cur);
n -= cur, cur = (cur > 1 ? 1 : 2);
}
puts("");
}
return 0;
}
CF1647B Madoka and the Elegant Gift
题意
给一个 01 矩阵,判断其是否有相交的极大 1 子矩阵
题解
std
很神奇的解法
如果没有相交的极大 1 子矩阵,那每个 1 联通块都是矩形
然后不知道为什么就突然发现了这样一个事实:
有 1 联通块不是矩形等价于存在至少一个 \(2 \times 2\) 子矩形中有 \(3\) 个 1
然后暴力判断就行
我的考场暴力
看到联通块,考虑暴力上并查集
对每个 \(1\) 联通块暴力维护行列坐标最大最小值以及联通块大小
然后暴力判断每个联通块行列坐标最大最小值之间夹的矩形面积是否等于联通块大小
我就说怎么 div2 的 B 都要用并查集
代码(std)
#include <bits/stdc++.h>
using namespace std;
void solve() {
int n, m;
cin >> n >> m;
vector<vector<int>> a(n, vector<int> (m));
for (int i = 0; i < n; ++i) {
string s;
cin >> s;
for (int j = 0; j < m; ++j) {
a[i][j] = s[j] - '0';
}
}
for (int i = 0; i < n - 1; ++i) {
for (int j = 0; j < m - 1; ++j) {
int sum = a[i][j] + a[i][j + 1] + a[i + 1][j] + a[i + 1][j + 1];
if (sum == 3) {
cout << "NO\n";
return;
}
}
}
cout << "YES\n";
}
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
int t;
cin >> t;
while (t--)
solve();
}
CF1647C Madoka and Childish Pranks
题意
给定一个 01 矩阵,其中 0 代表黑色,1 代表白色
Madoka 要对一个同样大小的 0 矩阵染色,每次染色可以将一个矩形染成国际象棋的颜色
现在问能否染成给定的 01 矩阵,如果可以,输出方案
题解
考虑上下或左右相邻的两个格子,如果将这个矩形染色,那么上(左)将会被染成白色,下(右)将会被染成黑色
那么我们考虑对第二行到最后一行染色,从下往上染,如果有一个格子需要染成黑色,那么我们将这个格子与其上面的格子组成的矩形染色即可
然后再对第一行的第二列到最后一列染色,从右往左染,如果有一个格子需要染成黑色,那么我们将这个格子与其左边面的格子组成的矩形染色即可
最后在考虑 \((1, 1)\),显然他只能是白色,所以如果 \((1, 1)\) 是黑色直接输出 NO 即可
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 110;
const int M = 10010;
int t, n, m, res, mp[N][N];
int main()
{
cin >> t;
while(t--){
cin >> n >> m, res = 0;
for(int i = 1; i <= n; i++){
getchar();
for(int j = 1; j <= m; j++) mp[i][j] = getchar() - '0', res += mp[i][j];
}
if(mp[1][1]){
puts("-1");
continue;
}
printf("%d\n", res);
for(int j = 1; j <= m; j++)
for(int i = n; i > 1; i--)
if(mp[i][j]) printf("%d %d %d %d\n", i - 1, j, i, j);
for(int j = m; j > 1; j--)
if(mp[1][j]) printf("%d %d %d %d\n", 1, j - 1, 1, j);
memset(mp, 0, sizeof(mp));
}
return 0;
}
CF1647D Madoka and the Best School in Russia
题意
给定整数 \(x\) 和 \(d\),保证有 \(d \mid x\)
设 \(tot\) 为将 \(x\) 拆分成若干个被 \(d\) 整除但不被 \(d^2\) 整除的数的乘积的方案数
判断 \(tot\) 是否大于 \(1\)
题解
设 \(x = d^a \times b\) 其中 \(d \nmid b\)
然后大力分类讨论
- \(a = 1\) 显然 \(tot \le 1\)
- \(a \ge 2\)
- \(b\) 为合数,显然 \(tot \ge 2\)
- \(b\) 为质数
- \(a = 2\) 则质因数分解 \(d\),若 \(d\) 存在一个质因子 \(p\) 满足 \(d \nmid p \times b\),则 \(tot > 1\) 反之 \(tot = 1\)
- \(a \ge 3\),若 \(d\) 为合数则 \(tot > 1\) 反之 \(tot = 1\)
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 110;
int t, x, d, pr[N], tms[N], cnt;
void div(int x)
{
cnt = tms[1] = 0;
for(int i = 2; i * i <= x; i++)
if(x % i == 0){
pr[++cnt] = i, tms[cnt] = 0;
while(x % i == 0) tms[cnt]++, x /= i;
}
if(x > 1) pr[++cnt] = x, tms[cnt] = 1;
}
int main()
{
ios :: sync_with_stdio(false), cin.tie(0);
cin >> t;
while(t--){
cin >> x >> d;
int tot = 0;
while(x % d == 0) tot++, x /= d;
if(tot == 1) puts("NO");
else{
div(x);
if(cnt > 1 || tms[1] > 1) puts("YES"); // 判断是否是合数
else if(tot == 2) puts("NO");
else if(tot == 3){
div(d);
bool flag = false;
for(int i = 1; i <= cnt && !flag; i++)
if(x * pr[i] % d) flag = true;
if(flag) puts("YES");
else puts("NO");
}
else{
div(d);
if(cnt > 1 || tms[1] > 1) puts("YES");
else puts("NO");
}
}
}
return 0;
}
CF1647E Madoka and the Sixth-graders
题意
有 \(n\) 个座位和好多好多个同学,初始时 \(1\) 到 \(n\) 号同学坐在座位上,\(n + 1\) 号及之后的同学只能站着
每天会换座位,将坐在第 \(i\) 个座位的同学换到第 \(p_i\) 个座位上,但是 \(p_i\) 有可能相同,所以只能让编号大的同学站着
既然 \(p_i\) 有可能相同,那就必然会有空着的座位,\(n+1\) 号及之后的同学按照编号从小到大依次找座位,每个人进去之后只会坐空着的座位中编号最小的那一个
好多天过去了,你知道现在每个座位坐着谁,你想知道初始时每个座位坐着谁
如果有多种可能,输出字典序最小的那一组
题解
显然 \(i\) 向 \(p_i\) 连边会构成基环内向树森林
首先,我们可以通过现在座位上编号最大同学的编号,以及有多少个座位的入度为 \(0\),推算出过了几天
然后,无论初始时座位是怎样的,\(t\) 天后 \(n+1\) 位及之后的同学的座位都不会变(因为他们坐座位时会是编号最大的,所以如果根前面的人有冲突肯定是他们站着)
那么对于初始时坐在 \(i\) 位置的同学,我们可以用倍增表快速得出他 \(t\) 天之后坐哪(如果他没有因为冲突站着的话),不妨设为 \(v_i\)
再设现在 \(i\) 位置上坐着 \(c_i\) 号同学
显然 \(c_{v_i} \le n\)
那么如果有一些 \(i\) 的 \(v_i\) 相同,那初始时他们的编号一定有一个是 \(c_{v_i}\),其他的都大于 \(c_{v_i}\)(都因为冲突站着了)
因为要字典序最小,所以我们得到一个算法:
算出 \(v\) 数组,从小到大枚举每个位置 \(i\)
如果 \(c_{v_i}\) 没被安排好,那就把它安排到第 \(i\) 个位置上
否则,第 \(i\) 个位置上就是最小的,比 \(c_{v_i}\) 大的,没被安排过的,并且不等于 \(c_{v_j} (\forall 1 \le j \le n)\) 的同学
容易证明这样可行且字典序最小
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
int n, r, tim, p[N], a[N], b[N], cur[N], in[N], to[N][35], nxt[N], used[N];
int walk(int x, int t)
{
for(int i = 30; i >= 0; i--)
if((1 << i) <= t) t -= (1 << i), x = to[x][i];
return x;
}
int find(int x)
{
if(!used[x]) return x;
return nxt[x] = find(nxt[x]);
}
int main()
{
cin >> n;
for(int i = 1; i <= n; i++) cin >> p[i], in[p[i]]++, to[i][0] = p[i], nxt[i] = i + 1;
for(int i = 1; i <= n; i++) if(!in[i]) r++;
int mx = 0;
for(int i = 1; i <= n; i++){
cin >> a[i], mx = max(a[i], mx);
if(a[i] <= n) used[a[i]] = 1;
}
tim = (mx - n) / r;
for(int i = 1; i <= 30; i++)
for(int j = 1; j <= n; j++) to[j][i] = to[to[j][i - 1]][i - 1];
for(int i = 1; i <= n; i++){
int x = walk(i, tim);
if(!cur[x]) b[i] = a[x], cur[x] = 1;
else b[i] = find(a[x]), used[b[i]] = 1;
}
for(int i = 1; i <= n; i++) cout << b[i] << " "; cout << endl;
return 0;
}
CF1647F Madoka and Laziness
题意
定义一个序列 \(a\) 为 “山” 等价于存在 \(t\) 满足 \(a_1 < a_2 < ... < a_t > a_{t+1} > a_{t+2} >...>a_n\),其中 \(t\) 称为山顶
给一个序列 \(b\),问将其拆分成两个子序列,且两个子序列都是山的方案数
两个方案不同当且仅当有一个山顶不同
题解
不管怎么分,\(b\) 序列的最大值必然是其中一个山顶,考虑枚举判断另一个山顶是否可行
如图
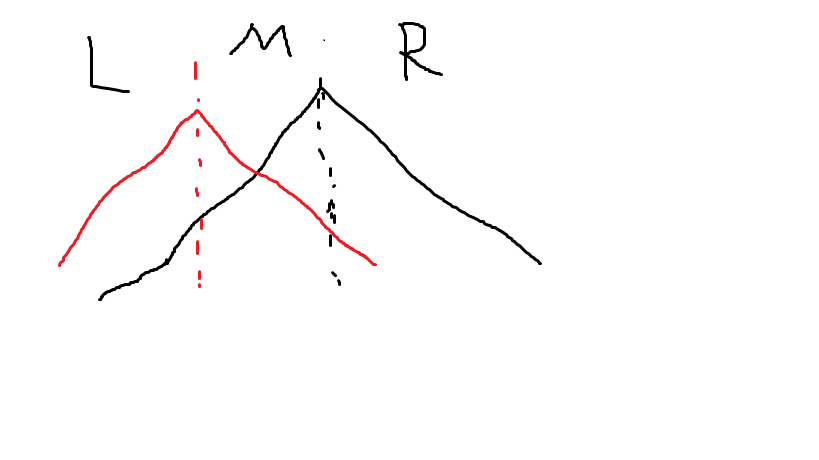
这张图是另一个山顶在最大值左边的情况,右边的类似
我们发现, \(L\) 部分需要满足能拆成两段上升子序列,\(M\) 部分需要满足能拆成一段上升,一段下降子序列,\(R\) 部分需要满足能拆成两段下降子序列,并且两个部分之间还要满足能拼接起来
众所周知,一段序列能拆成 \(k\) 段上升子序列等价于最长下降子序列长度小于等于 \(k\)
然而这里 \(k\) 只有 \(2\),并且如果求最长下降子序列的话还不好拼接
所以考虑直接 dp
设 \(f_i\) 为一段上升序列以 \(i\) 结尾,另一段上升序列末尾的最小高度
则
- \(b_i > b_{i-1}, f_{i-1} -> f_i\)
- \(b_i > f_{i-1}, b_{i-1} -> f_i\)
这个 dp 其实还用到了换维的思想,朴素的 dp 应该是 \(f_{i, j}\) 表示一段上升序列以 \(i\) 结尾,另一段以 \(j\) 结尾是否可行
但我们发现这样的话 \(f_{i, j}\) 的值域只有 \(\{0, 1\}\),这一维非常小,我们考虑将这一维和 \(i\) 或 \(j\) 换掉,再综合分析转移方程得出了这个 dp
其他子问题类似,一段上升,一段下降稍微复杂一点,但也没有本质区别
为了方便下面描述,这里把状态说明一下(与下面的代码对应)
- 最大值的位置为 \(pos\)
- 将从 \(1\) 到 \(i\) 的序列分割为两个上升子序列,其中一个以 \(i\) 结尾,另一个末尾的最小值为 \(t_i\)
- 将从 \(n\) 到 \(i\) 的序列分割为两个上升子序列 (这里是从 \(n\) 到 \(i\),所以是上升),其中一个以 \(i\) 结尾,另一个末尾的最小值为 \(k_i\)
- 将从 \(pos\) 到 \(i\) 的序列分割为一个上升,一个下降的子序列,其中下降子序列以 \(i\) 结尾,上升子序列末尾的最小值为 \(f_i\)
- 将从 \(pos\) 到 \(i\) 的序列分割为一个上升,一个下降的子序列,其中上升子序列以 \(i\) 结尾,下降子序列末尾的最大值为 \(g_i\)
将所有子问题解决后 \(i\)(\(i\) 在最大值左边) 能成为另一个山顶当且仅当
- \(t_i < inf\),即有一种方法将 \(1\) 到 \(i\) 分割为两个上升子序列
- \(t_i < g_i\),最大值左边的下坡段需要满足单调递减
- \(k_{pos} < inf\),即最大值右边分为两个下降子序列的分割存在
注意为了满足 \(2, 3\) 点能成功拼接,dp 一段上升,一段下降的子序列时,应该将 \(f_{pos}\) 设为 \(k_{pos}\),满足最大值右边的下坡段单调
另一个山顶在最大值右边的情况类似,不再赘述
复杂度 \(O(n)\)
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 500010;
const int inf = 0x3f3f3f3f;
int n, mx, pos, ans, a[N], v[N], f[N], g[N], t[N], k[N];
int can[N];
int main()
{
scanf("%d", &n);
for(int i = 1; i <= n; i++) scanf("%d", a + i), v[i] = a[i];
std :: sort(v + 1, v + n + 1);
for(int i = 1; i <= n; i++){
a[i] = std :: lower_bound(v + 1, v + n + 1, a[i]) - v;
if(a[i] > mx) mx = a[i], pos = i;
}
for(int i = 1; i <= pos; i++){
t[i] = inf;
if(a[i] > a[i - 1]) t[i] = min(t[i], t[i - 1]);
if(a[i] > t[i - 1]) t[i] = min(t[i], a[i - 1]);
}
for(int i = n; i >= pos; i--){
k[i] = inf;
if(a[i] > a[i + 1]) k[i] = min(k[i], k[i + 1]);
if(a[i] > k[i + 1]) k[i] = min(k[i], a[i + 1]);
}
f[pos] = t[pos], g[pos] = inf; //设定 dp 初始值
for(int i = pos + 1; i <= n; i++){
f[i] = inf, g[i] = 0;
if(a[i] < a[i - 1]) f[i] = min(f[i], f[i - 1]);
if(a[i] < g[i - 1]) f[i] = min(f[i], a[i - 1]);
if(a[i] > a[i - 1]) g[i] = max(g[i], g[i - 1]);
if(a[i] > f[i - 1]) g[i] = max(g[i], a[i - 1]);
if(f[i] == inf && g[i] == 0) break;
if(k[i] < g[i] && g[i]) ans++;
}
f[pos] = k[pos], g[pos] = inf;
for(int i = pos - 1; i >= 1; i--){
f[i] = inf, g[i] = 0;
if(a[i] < a[i + 1]) f[i] = min(f[i], f[i + 1]);
if(a[i] < g[i + 1]) f[i] = min(f[i], a[i + 1]);
if(a[i] > a[i + 1]) g[i] = max(g[i], g[i + 1]);
if(a[i] > f[i + 1]) g[i] = max(g[i], a[i + 1]);
if(f[i] == inf && g[i] == 0) break;
if(t[i] < g[i] && g[i]) ans++;
}
printf("%d\n", ans);
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号