题解 [WC2011] 最大XOR和路径

题目链接

Luogu

题目描述

给定 \(n\) 个点 , \(m\) 条边的带权无向图 , 问所有 \(1\) 到 \(n\) 的路径中 , 边权异或和最大是多少

其中 \(n \le 50000, m \le 100000\) , 且可能有重边和自环

分析

首先 , 看到最大异或和 , 我们很自然的想到用线性基去处理

但线性基对最大异或和的限制十分严格 , 需要数字之间能任意异或 , 而本题需要选取的边是一条 \(1\) 到 \(n\) 的路径

如何把题目转化成可以随便异或的形式呢 ?

仔细观察会发现 , 所有简单路径都可以等价表示为任意一条 \(1\) 到 \(n\) 的简单路径加上一个过 \(n\) 点的环

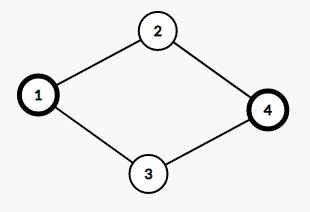
如路径 \(1 -> 3 -> 4\) 可以表示为 \(1 -> 2 -> 4 -> 2 -> 1 -> 3 -> 4\)

其中 \(4 -> 2 -> 1 -> 3 -> 4\) 就是一个过点 \(4\) 的环

那我们再考虑不是简单路径的路径

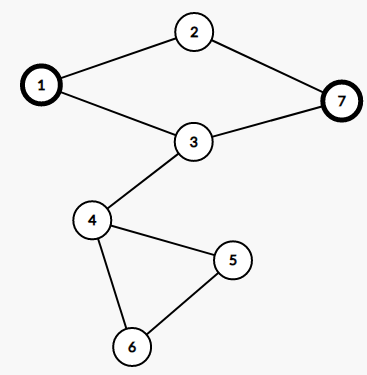
路径 \(1 -> 3 -> 4 -> 5 -> 6 -> 4 -> 3 -> 7\) 中 \(3 -> 4\) 这条边经过了两次 , 由异或运算的性质可知这条边不计入贡献 , 所以这条路径可以表示为简单路径 \(1 -> 3 -> 7\) 再加上 不过 点 \(7\) 的环 \(4 -> 5 -> 6 -> 4\)

那如果我们选的简单路径是 \(1 -> 2 -> 7\) 那刚刚那条路径可以表示为简单路径 \(1 -> 2 -> 7\) 加上环 \(7 -> 2 -> 1 -> 3 -> 7\) 再加上环 \(4 -> 5 -> 6 -> 4\)

也就是一条好长好长的路径 \(1 -> 2 -> 7 -> 2 -> 1 -> 3 -> 7 -> 3 -> 4 -> 5 -> 6 -> 4 -> 3 -> 7\)
其中 \(1 -> 2, 2 -> 7, 3 -> 4\) 经过了两次 , \(3 -> 7\) 被经过了三次

所以我们猜测所有 \(1\) 到 \(n\) 的路径都可以表示为 任意一条 \(1\) 到 \(n\) 的简单路径加上任意个环

而当图联通的情况下 , 任意一条 \(1\) 到 \(n\) 的简单路径加上任意个环也显然可以表示一条 \(1\) 到 \(n\) 的路径

这样我们终于把题目转化成了线性基能做的形式

只要我们把所有环插入线性基内 , 再以任意一条简单路径为初始值跑一遍线性基 , 最大异或和就是答案啦

但是我们发现 , 当可能出现重边时 , 图中的环的个数是指数级别的

那如何将这些环放进线性基里呢 ?

仔细观察发现 , 有些环可以等价的用其他环表示

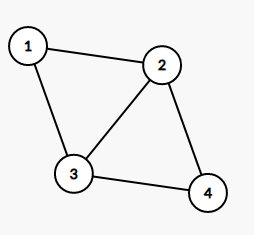
如环 \(1 -> 2 -> 4 -> 3 -> 1\) 可以表示为环 \(1 -> 2 -> 3 -> 1\) 加上环 \(3 -> 2 -> 4 -> 3\)
即路径 \(1 -> 2 -> 3 -> 1 -> 3 -> 2 -> 4 -> 3 -> 1\) , 其中 \(2 -> 3\) 经过两次 , \(1 -> 3\) 经过三次

那么 , 在先插入后面两个环的情况下 , 即使我们把环 \(1 -> 2 -> 4 -> 3 -> 1\) 插入线性基中 , 它也不会使线性基发生任何变化

也就是说 , 一个无向连通图存在一个由若干个环构成的基 , 且这张图中所有的环都可以由基中的环异或得到

如果我们找到了这个基 , 并将基中的环插入线性基内 , 那就相当于我们把图中的所有环插入线性基内了

那这个基又是什么呢 ?

个人感觉这里是这道题最神奇的地方 , 我实在是编不出这个解法的脑回路 , 于是只能直接讲结论了

建出无向图的 DFS 树 , 基就是那些 由一条非树边和若干条树边构成的环的集合

显然 , 一条非树边和若干条树边只能构成一个环
我们假设由非树边 \(e\) 和若干条树边构成的环的异或和为 \(v_e\)

首先 , 对于仅由树边构成的环 , 这样的环不存在
然后 , 对于一条非树边和若干条树边构成的环 , 它就在基里面
最后 , 对于由若干条非树边 \(e_1, e_2, ... e_k\) 和若干条树边构成的环 , 他的异或和就是 \(v_{e_1} \oplus v_{e_2} \oplus .... \oplus v_{e_k}\)

因为两个环异或就相当于他们的边集的并再去掉边集的交

非树边共 \(m - n + 1\) 条 , 所以基中的环有 \(m - n + 1\) 个 , 将他们插进线性基中 , 复杂度为 \(O((m - n) \log V)\) 其中 \(V\) 为边权大小

至此本题解决

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;

const int N = 50010;
const int M = 200010;

LL n, m, cnt, k, head[N], to[M], nxt[M], w[M], st[N], d[N], vis[N]; // st为线性基 , d为DFS树上点的深度（d[n]当然就是一条简单路径的长度）

inline void addedge(int u, int v, LL k)
{
    to[++cnt] = v;
    nxt[cnt] = head[u], head[u] = cnt, w[cnt] = k;
}

void add(LL x)
{
    if(!x) return ;
    for(int i = 63; i >= 0; i--){
        if(!(x >> i)) continue;
        if(!st[i]){
            st[i] = x;
            break;
        }
        x ^= st[i];
    }
}

LL que(LL x)
{
    for(int i = 63; i >= 0; i--)
        if((x ^ st[i]) > x) x ^= st[i];
    return x;
}

void dfs(int x, LL dist)
{
    d[x] = dist, vis[x] = 1;
    for(int i = head[x]; i; i = nxt[i]){
        if(!vis[to[i]]) dfs(to[i], dist ^ w[i]);  // 如果to[i]未被访问 , 说明i是树边
        else add(w[i] ^ dist ^ d[to[i]]); // i是非树边 , to[i] 和 x 的 lca 以上的边异或了两次 , 留下的就只有一个环
    }
}

int main()
{
    ios :: sync_with_stdio(false);
    cin >> n >> m;
    for(int i = 1, u, v; i <= m; i++){
        cin >> u >> v >> k;
        addedge(u, v, k);
        addedge(v, u, k);
    }
    dfs(1, 0);
    printf("%lld\n", que(d[n]));
    return 0;
}