线性代数-标量、向量、矩阵、张量
本文从标量、向量入手,讲解到矩阵、张量,并讲解了矩阵与张量的运算规则,对于神经网络来说,张量之间更多的是:矩阵相乘 (卷积提取特征)、矩阵内积 (transformer 计算自注意力)
什么是标量 (scalar)?
- 一个标量表示一个单独的数
>>> x=torch.tensor([3.0]) >>> y=torch.tensor([2.0]) >>> x+y,x*y,x/y,x**y (tensor([5.]), tensor([6.]), tensor([1.5000]), tensor([9.]))
什么是向量(vector)?
- 由标量(scalar)组成的列表,标量值称为向量的元素或分量
- 通常赋予向量粗体的小写变量名称,比如xx。向量中的元素可以通过带脚标的斜体表示。向量𝑋的第一个元素是𝑋1,第二个元素是𝑋2
>>> x=torch.arange(6) >>> x tensor([0, 1, 2, 3, 4, 5]) # 使用下标访问 >>> x[3:] tensor([3, 4, 5]) # 获取向量属性 >>> len(x) 6 >>> x.shape torch.Size([6])
什么是矩阵(matrix)?
- 向量(vector)将标量(scalar)从零阶推广到一阶,矩阵将向量从一阶推广到二阶
>>> import torch >>> torch.arange(20).reshape(5,4) tensor([[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11], [12, 13, 14, 15], [16, 17, 18, 19]])
什么是张量(tensor)?
- 就像向量(vector)是标量(scalar)的推广,矩阵(matrix)是向量的推广一样,张量指具有任意数量轴的n维数组的通用方法
>>> import torch >>> A=torch.arange(20).reshape(5,4) >>> B=A.clone() >>> A+B tensor([[ 0, 2, 4, 6], [ 8, 10, 12, 14], [16, 18, 20, 22], [24, 26, 28, 30], [32, 34, 36, 38]])
标量、向量、矩阵、张量之间的关系?
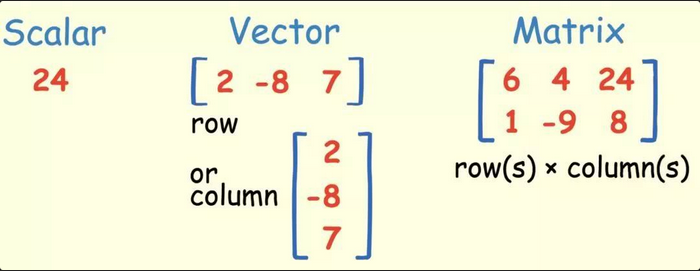
- 标量(scalar)是0阶张量,向量(vector)是一阶张量,矩阵(matrix)是二阶张量
- 标量就是知道棍子的长度,但是你不会知道棍子指向哪儿
- 向量就是不但知道棍子的长度,还知道棍子指向前面还是后面
- 张量就是不但知道棍子的长度,也知道棍子指向前面还是后面,还能知道这棍子又向上/下和左/右偏转了多少
向量的数乘?
- 一个数乘以向量中的每个元素
2×(123)=(246)
向量的内积 (点积、数量积、标量积、dot product)?
-
又称数量积或标量积,是一种接受两个等长的数字序列(通常是坐标向量)、返回单个数字的代数运算
(0123)(1111)=0×1+1×1+2×1+3×1=6
>>> import torch >>> x=torch.arange(4,dtype=torch.float) >>> y=torch.ones(4,dtype=torch.float32) >>> x,y,torch.dot(x,y) (tensor([0., 1., 2., 3.]), tensor([1., 1., 1., 1.]), tensor(6.)) # torch.dot应用非1D张量上会报错 >>> x,y=torch.arange(6).reshape(3,2),torch.ones(2).reshape(2,1) >>> x,y,torch.dot(x,y) Traceback (most recent call last): File "", line 1, in RuntimeError: 1D tensors expected, but got 2D and 2D tensors
向量的外积(叉积、叉乘、向量积)?
-
与点积不同,它的运算结果是向量,并且两个向量的叉积与这两个向量组成的坐标平面垂直
-
对于2个向量,𝑎=(𝑥1,𝑦1,𝑧1),𝑏=(𝑥2,𝑦2,𝑧2) ,外积如下,其中𝑖=(1,0,0)j=(0,1,0)k=(0,0,1)
𝑎×𝑏=|ijk𝑥1𝑦1𝑧1𝑥2𝑦2𝑧2|=(𝑦1𝑧2−𝑦2𝑧1,−(𝑥1𝑧2−𝑥2𝑧1),𝑥1𝑦2−𝑥2𝑦1)
-
在三维几何中,向量a和向量b的叉乘结果是一个向量,更为熟知的叫法是法向量,该向量垂直于a和b向量构成的平面;如果两个向量方向相同或相反(即它们没有线性无关的分量),亦或任意一个的长度为零,那么它们的外积为零
矩阵的数乘?
- 用一个数乘以矩阵中的每个元素
5×[123000]=[51015000]
矩阵和向量相乘?
-
矩阵和向量相乘表示对矩阵进行遍历求和
>>> A,x=torch.arange(20,dtype=torch.float32).reshape(5,4),torch.ones(4,dtype=torch.float32) >>> A tensor([[ 0., 1., 2., 3.], [ 4., 5., 6., 7.], [ 8., 9., 10., 11.], [12., 13., 14., 15.], [16., 17., 18., 19.]]) >>> x tensor([1., 1., 1., 1.]) >>> A.shape,x.shape,torch.mv(A,x) (torch.Size([5, 4]), torch.Size([4]), tensor([ 6., 22., 38., 54., 70.]))
矩阵之间的乘法?
- 线性代数里面的矩阵乘法,要求第一个矩阵的列数和第二个矩阵的行数相等
𝐶=𝐴𝐵=(123456)(142536)=(1×1+2×2+3×31×4+2×5+3×64×1+5×2+6×34×4+5×5+6×6)=(14323277)
矩阵之间的哈达玛积(Hadamard product)?
- 两个相乘的矩阵维度一致,逐元素相乘(矩阵点乘)
>>> import torch >>> A=torch.arange(20).reshape(5,4) >>> A tensor([[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11], [12, 13, 14, 15], [16, 17, 18, 19]]) >>> B=A.clone() >>> A*B tensor([[ 0, 1, 4, 9], [ 16, 25, 36, 49], [ 64, 81, 100, 121], [144, 169, 196, 225], [256, 289, 324, 361]])
矩阵之间的克罗内克积(Kronecker product)?
- 两个任意大小的矩阵间的运算,被称为直积或张量积
[1231]⊗[0321]=[1⋅01⋅32⋅02⋅31⋅21⋅12⋅22⋅13⋅03⋅31⋅01⋅33⋅23⋅11⋅21⋅1]=[0306214209036321]
什么是方程组?
-
形式如下:
{2𝑥−𝑦=0−4𝑥+2𝑦=0
-
把方程组中所有系数写到了一个矩阵(matrix)里面,把所有未知数写到第二个框里,把所有等式右边的值写到第三个框里
[2−1−42][𝑥1𝑥2]=[00]
-
增广矩阵:将上面内容矩阵形式改为增广矩阵
[2−10−420]
-
方程组的等式右边全为0的方程组为齐次线性方程组,否则为非齐次线性方程组
方程组的初等变换?
-
现有方程组
{𝑥+2𝑦+𝑧=23𝑥+8𝑦+𝑧=124𝑦+𝑧=2
-
表示为增广矩阵
[1212381120412]
-
消除(2,1)位置的元素,通过 Row 2=Row2+Row1×(−3) ,得
[13212381120412]→(2,1)[121202−260412]
-
消除(3,2)位置的元素,通过 Row3 = Row3 + Row 2×(−2) ,得
[1212024−260412]→(3,2)[121202−26005−10]
-
消元后的矩阵等式为
[12102−2005][𝑥𝑦𝑧]=[26−10]
-
解得, 𝑥=2,𝑦=1,𝑧=−2
什么是范数?
- 在线性代数中,向量范数是将向量映射到标量的函数f
>>> u=torch.tensor([3.0,4.0]) # L1范数 >>> torch.abs(u).sum() tensor(7.) # L2范数 >>> torch.norm(u) tensor(5.) - 一个向量的范数告诉我们一个向量有多大。这里考虑的大小(size)概念不涉及维度,而是分量的大小
向量范数的归纳?
-
定义一个向量为:𝑎→=[−5,6,8,−10]。任意一组向量设为𝑥→=(𝑥1,𝑥2,…,𝑥𝑁)。其不同范数求解如下
-
向量的1范数:向量的各个元素的绝对值之和,上述向量𝑎→的1范数结果就是:29
‖𝑥→‖1=∑𝑖=1𝑁|𝑥𝑖|
-
向量的2范数:向量的每个元素的平方和再开平方根,上述𝑎→的2范数结果就是:15
‖𝑥→‖2=∑𝑖=1𝑁|𝑥𝑖|2
-
向量的负无穷范数:向量的所有元素的绝对值中最小的:上述向量𝑎→的负无穷范数结果就是:5
‖𝑥→‖−∞=min|𝑥𝑖|
-
向量的正无穷范数:向量的所有元素的绝对值中最大的:上述向量𝑎→的正无穷范数结果就是:10
‖𝑥→‖+∞=max|𝑥𝑖|
-
向量的p范数
𝐿𝑝=‖𝑥→‖𝑝=∑𝑖=1𝑁|𝑥𝑖|𝑝𝑝
矩阵的范数归纳?
-
定义一个矩阵𝐴=[−1,2,−3;4,−6,6]。 任意矩阵定义为:𝐴𝑚×𝑛,其元素为 𝑎𝑖𝑗 , 矩阵的范数定义为
‖𝐴‖𝑝:=sup𝑥≠0‖𝐴𝑥‖𝑝‖𝑥‖𝑝
-
矩阵的1范数(列范数):矩阵的每一列上的元素绝对值先求和,再从中取个最大的,(列和最大),上述矩阵𝐴的1范数先得到[5,8,9],再取最大的最终结果就是:9
‖𝐴‖1=max1≤𝑗≤𝑛∑𝑖=1𝑚|𝑎𝑖𝑗|
-
矩阵的2范数:矩阵𝐴𝑇𝐴的最大特征值开平方根,上述矩阵𝐴的2范数得到的最终结果是:10.0623 , 其中, 𝜆𝑚𝑎𝑥(𝐴𝑇𝐴) 为 𝐴𝑇𝐴 的特征值绝对值的最大值
‖𝐴‖2=𝜆𝑚𝑎𝑥(𝐴𝑇𝐴)
-
矩阵的无穷范数(行范数):矩阵的每一行上的元素绝对值先求和,再从中取个最大的,(行和最大),上述矩阵𝐴的行范数先得到;[6;16],再取最大的最终结果就是:16
‖𝐴‖∞=max1≤𝑖≤𝑚∑𝑗=1𝑛|𝑎𝑖𝑗|
-
矩阵的核范数:矩阵的奇异值(将矩阵svd分解)之和,这个范数可以用来低秩表示(因为最小化核范数,相当于最小化矩阵的秩——低秩),上述矩阵A最终结果就是:10.9287
-
矩阵的L0范数:矩阵的非0元素的个数,通常用它来表示稀疏,L0范数越小0元素越多,也就越稀疏,上述矩阵𝐴最终结果就是:6
-
矩阵的L1范数:矩阵中的每个元素绝对值之和,它是L0范数的最优凸近似,因此它也可以表示稀疏,上述矩阵𝐴最终结果就是:22
-
矩阵的F范数:矩阵的各个元素平方之和再开平方根,它通常也叫做矩阵的L2范数,它的优点在于它是一个凸函数,可以求导求解,易于计算,上述矩阵A最终结果就是:10.0995
‖𝐴‖𝐹=(∑𝑖=1𝑚∑𝑗=1𝑛|𝑎𝑖𝑗|2)
-
矩阵的L21范数:矩阵先以每一列为单位,求每一列的F范数(也可认为是向量的2范数),然后再将得到的结果求L1范数(也可认为是向量的1范数),很容易看出它是介于L1和L2之间的一种范数,上述矩阵𝐴最终结果就是:17.1559
-
矩阵的 p范数
‖𝐴‖𝑝=(∑𝑖=1𝑚∑𝑗=1𝑛|𝑎𝑖𝑗|𝑝)𝑝
如何判定矩阵为正定的?
- 顺序主子式全大于0
- 存在可逆矩阵𝐶使𝐶𝑇𝐶等于该矩阵
- 正惯性指数等于𝑛
- 合同于单位矩阵𝐸(即:规范形为𝐸)
- 标准形中主对角元素全为正
- 特征值全为正
- 是某基的度量矩阵
什么是矩阵的特征值 (eigenvalue)、特征向量 (eigenvectors)?
- 对于方阵 A,特征向量 𝑣 和特征值 𝜆 使此方程成立
标量、向量、矩阵、张量-20230408153026-1
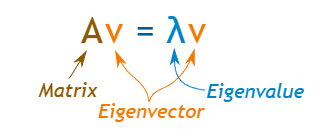
- 举例:以上公式矩阵乘以向量,并得到与将标量(只是一个数字)乘以该向量时相同的结果
标量、向量、矩阵、张量-20230408153027
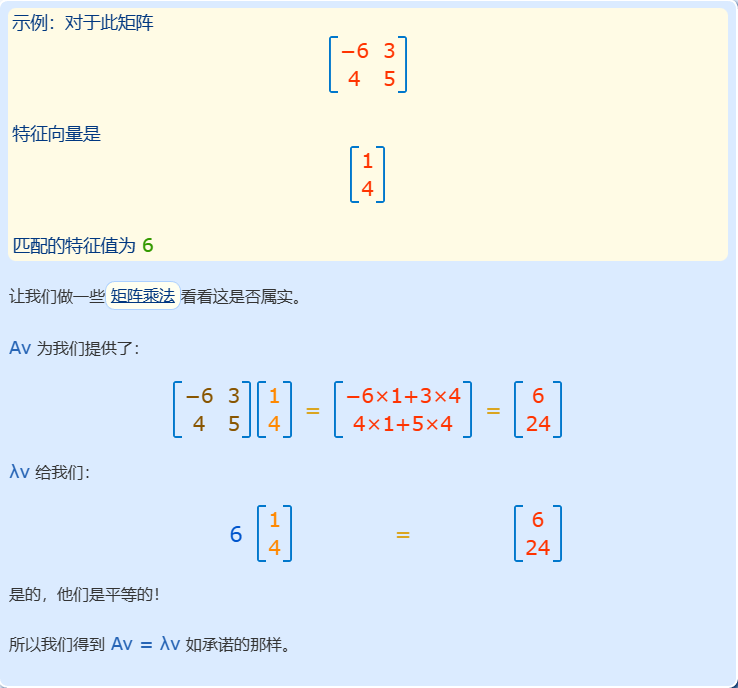
如何求特征值与特征向量?
-
标量、向量、矩阵、张量-20230408153027-1

- (1)从找到特征值开始,已知以下等式一定是正确的$$ A\nu = \lambda \nu $$
- (2)加入一个恒等矩阵
𝐴𝜈=𝜆𝐼𝜈
- (3) 如果 𝑣 不为 0,去掉后得到以下式子,在此基础上求解特征值
∣𝐴𝜈−𝜆𝜈∣=0
- (4)得到特征值后,带入式子 (1)求解特征向量
奇异值与特征值有什么关系?
-
将一个矩阵𝐴的转置乘以𝐴,并对𝐴𝑇𝐴求特征值,则有下面的形式
(𝐴𝑇𝐴)𝑉=𝜆𝑉
-
这里𝑉就是上面的右奇异向量,另外还有
𝜎𝑖=𝜆𝑖,𝑢𝑖=1𝜎𝑖𝐴𝑉
这里的𝜎就是奇异值,𝑢就是上面说的左奇异向量,奇异值𝜎跟特征值类似,在矩阵∑中也是从大到小排列,而且𝜎的减少特别的快,在很多情况下,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了, 也就是说,我们也可以用前 𝑟 ( 𝑟 远小于 、𝑚、𝑛)个的奇异值来近似描述矩阵,即部分奇异值分解:
𝐴𝑚×𝑛≈𝑈𝑚×𝑟∑𝑟×𝑟𝑉𝑟×𝑛𝑇
-
右边的三个矩阵相乘的结果将会是一个接近于𝐴的矩阵,在这儿,𝑟越接近于𝑛,则相乘的结果越接近于𝐴
本文使用 Zhihu On VSCode 创作并发布




 浙公网安备 33010602011771号
浙公网安备 33010602011771号