【凸优化】3 多面体，单纯形，半正定锥

1 多面体 Polyhedra

定义：多面体为一系列的（有限个）线性等式和不等式的解集：

\[\mathcal{P}=\{x|a_j^T x \leq b_j, j=1,...,m, c_j^Tx = d_j, j = 1,...,p \} \]

根据上式可看出，多面体是\(m\)个半空间和\(p\)个超平面的交集，其中\(m,n\)为非无穷的正数。
仿射集（直线、子空间、超平面）、射线、线段、半空间都是多面体，多面体是凸集。

多面体的另一种表示：

\[\mathcal{P}=\{x|Ax \preceq b, Cx = d \} \]

其中

\[A=\begin{bmatrix} a_1^T\\ ...\\ a_m^T\\ \end{bmatrix}, C=\begin{bmatrix} c_1^T\\ ...\\ c_p^T\\ \end{bmatrix} \]

其中符号\(\preceq\)表示\(\mathbb{R}^m\)空间内的向量号不等或分量不等号，例如\(u\preceq v\)表示\(u_i \leq v_i\)，\(i = 1,...,m\)。

2 单纯形 Simplexes

1）定义

定义：在\(\mathbb{R}^n\)空间中选取\(k+1\)个仿射独立(affinely independent)的点，即\(v_1 - v_0,...,v_k-v_0\)是线性无关的，则与上述点相关的单纯形为：

\[C={\rm conv}\; \{v_0,...,v_k\}=\{\theta_0 x_0+...+\theta_k x_k| \theta\succeq 0,\mathbf{1}^T\theta = 1\} \]

其中\({\rm conv}\)表示凸包，\(\mathbf{1}\)表示所有元素均为\(1\)的向量。该单纯形的仿射维数为\(k\)，称为\(k\)维单纯形。

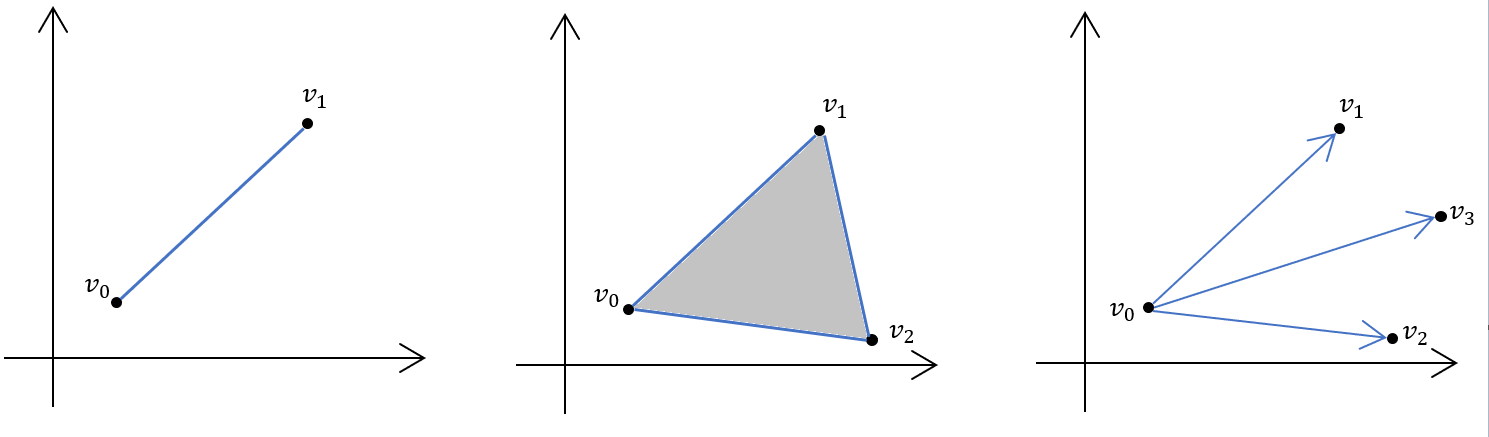
图1. \(\mathbb{R}^2\)空间中，左：\(k=1\)，选取两个点得到的单纯形为一个线段；中：\(k=2\)，选三个点，相关的单纯形为一个三角形（包括边和阴影部分）；右：\(k=3\)，选取四个点，但是在二维空间中无法找到三个线性无关的向量（图中的任一向量可由另两个向量的线性组合得到），故在二维空间中，无法找到四个或以上的点来构成一个单纯形。

如图1，同样的可以得出：一维空间中的单纯形是线段；二维空间中的单纯形是三角形；三维空间中的单纯形为四面体。

2）证明：单纯形是多面体的一种

\(C\in\mathbb{R}^n\)为单纯形，则根据单纯形的定义可得：

\[x\in C\Leftrightarrow x=\theta_0 v_0 + ...+ \theta_k v_k,\mathbf{1}^T\theta = 1,\theta\succeq 0,v_1 - v_0,...,v_k-v_0线性无关 \tag{1} \]

为方便表示，我们定义\(y\) 和 \(B\)：

\[y=[\theta_1,...,\theta_k]^T, \;\; y\succeq 0, \;\; \mathbf{1}^T y \leq 1 \]

\[B=\begin{bmatrix} v_1-v_0 & ... & v_k-v_0 \end{bmatrix}\in \mathbb{R}^{n\times k}\]

则公式（1）可以表示为：

\[x\in C \Leftrightarrow x=v_0 + By\tag{2} \]

\(v_0, ..., v_k\)为仿射独立的，即\(v_1-v_0,...,v_k-v_0\)为线性无关的，可得\({\rm rank}(B)=k\)，\((k\leq n)\)，因此存在一个非奇异矩阵\(A=\begin{bmatrix}A_1 \\A_2\end{bmatrix}\in\mathbb{R}^{n\times n}\)使得

\[AB=\begin{bmatrix}A_1 \\A_2\end{bmatrix} B=\begin{bmatrix}I\\0\end{bmatrix},\;(I\in \mathbb{R}^{k\times k}) \]

对公式（2）左乘一个矩阵\(A\)：

\[\begin{aligned} Ax &= Av_0 + ABy\\ \begin{bmatrix}A_1 \\A_2\end{bmatrix}x &=\begin{bmatrix}A_1 \\A_2\end{bmatrix}v_0+\begin{bmatrix}I\\0\end{bmatrix}y \end{aligned} \]

即

\[\left\{\begin{matrix} A_1 x=A_1 v_0 + y\\ A_2 x=A_2 v_0 \end{matrix}\right. \]

因此\(x\in C\) 当且仅当 \(A_2 x= A_2 v_0\)且向量\(y=A_1x - A_1 v_0\)满足\(y\succeq 0, \; \mathbf{1}^T y \leq 1\)。换句话说，\(x\in C\) 当且仅当:

\[A_2 x = A_2 v_0, \;\;\; A_1 x \succeq A_1 v_0, \;\;\; \mathbf{1}^TA_1x \leq 1+ \mathbf{1}^T A_1 v_0 \]

即单纯形为两个不等式和一个等式描述的集合，这也就是多面体的定义。

3 半正定锥 The Positive Semidefinite Cone

1)定义

对称矩阵的集合 \(\textbf{S}^n\):

\[\textbf{S}^n = \{X\in \mathbb{R}^{n\times n}|X=X^T\} \]

这是一个维度为 \(n(n + 1)/2\) 的向量空间。
是凸锥，所以也是凸集。
对称半正定矩阵的集合 \(\textbf{S}^n_+\):

\[\textbf{S}^n_+ = \{X\in \textbf{S}^n|X\succeq 0\} \]

这里的符号\(\succeq\)是针对矩阵的，表示\(X\)的奇异值大于等于0。
是凸锥，所以也是凸集。
对称正定矩阵的集合 \(\textbf{S}^n_{++}\):

\[\textbf{S}^n_{++} = \{X\in \textbf{S}^n|X\succ 0\} \]

是凸集，不是凸锥。

2）证明：\(\textbf{S}^n_+\)是凸锥

即（根据凸锥的定义）任取\(\theta_1, \theta_2 \geq 0\)，\(A, B \in \textbf{S}^n_+\)，证明\(\theta_1 A+\theta_2 B\in \textbf{S}^n_+\)。
根据半正定矩阵的性质有：

\[\forall x\in \mathbb{R}^n,\; x^T A x \geq 0,\; x^T B x \geq 0 \]

因此：

\[\begin{aligned} &x^T(\theta_1 A+\theta_2 B)x\\ =&\;\theta_1x^T A x + \theta_2 x^T B x\\ \geq & \; 0 \end{aligned} \]

即\(\theta_1 A+\theta_2 B\in \textbf{S}^n_+\)，证明完毕。

3）不同空间中的特征

n=1：即一维空间中，\(\textbf{S}^1 = \textbf{R}\)（实数集）；\(\textbf{S}^1_+ = \textbf{R}_+\)（非负实数集）；\(\textbf{S}^1_{++} = \textbf{R}_{++}\)（正实数集)。
n=2：即二维空间中，如图2，我们有：

\[X = \begin{bmatrix}x & y\\ y & z\end{bmatrix}\in \textbf{S}^2_+ \Leftrightarrow x \geq 0, z \geq 0, xz \geq y^2 \]

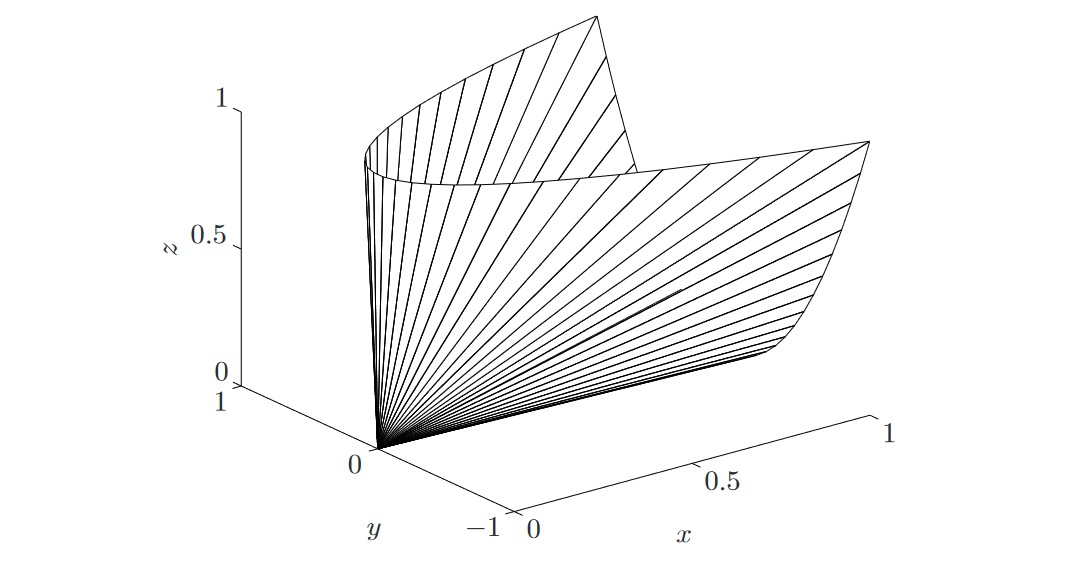
图2. 二维空间中半正定锥的边界，在\(\mathbb{R}^3\)中绘制为 \((x, y, z)\)。