Learning Rate Based Branching Heuristic for SAT Solvers
1. 预备知识
1.1 Simple Average and Exponential Moving Average
给定一个含有时间序列的数字序列\(S_n=<r_1,r_1,r_2, ..., r_n>\)
- simple average 的计算方式为 \(avg(S_n)=\sum_{i=1}^N \frac 1n*r_i\),在这里每个\(r_i\)的系数(权重)都是一样的,即\(\frac 1n\)
- exponential moving average (EMA) 的计算方法为\(ema_\alpha(S_n)=\sum_{i=1}^N\alpha*(1-\alpha)^{n-i}*r_i (0\lt\alpha\lt1)\),其中\(\alpha\)被称为
step-size。另外一种计算方法为\(ema_\alpha(S_n)=(1-\alpha)ema_\alpha(S_{n-1})+\alpha*r_n\),其中\(ema_\alpha(<>)=0\)。当\(S\)最近的新数据比以前的老数据更重要时(例如股票),这时就不能用simple average的计算方法了,因为需要对新的数据赋予更大的权重,对老数据赋予更小的权重。 ^2a28b5
1.2 Multi-Armed Bandit (MAB)
在多臂赌博机(multi-armed bandit,MAB)问题(见下图),有一个拥有\(n\)根拉杆的赌博机,拉动每一根拉杆都对应一个关于奖励的概率分布\(R\)。我们每次拉动其中一根拉杆,就可以从该拉杆对应的奖励概率分布中获得一个奖励\(a\)。我们在各根拉杆的奖励概率分布未知的情况下,从头开始尝试,目标是在操作 \(T\)次拉杆后获得尽可能高的累积奖励。由于奖励的概率分布是未知的,因此我们需要在“探索拉杆的获奖概率”和“根据经验选择获奖最多的拉杆”中进行权衡。“采用怎样的操作策略才能使获得的累积奖励最高”便是多臂赌博机问题。

假如这里有两台赌博机,一个人分别对两台赌博机拉了四次拉杆,得到奖励的时间序列分别是\(S_1=<1,2,3,4>,S_2=<5,4,3,2>\)。进行一下次动作之前,需要计算两台赌博机奖励的概率分布\(R_1,R_2\)。采用simple average计算方法,\(R_1=avg(S_1)=2.5,R_2=avg(S_2)=3.5\),因为2号赌博机的R大,为了使得累积奖励最高,下一次动作就会拉动2号赌博机的拉杆,执行这种基于目前观察的最好的动作就被称之为greedy,而选择non-greedy的动作被称之为exploration。
有一个问题,simple average只适用于R固定的情况。如果随着时间的推移,R也在逐渐的变化,这中问题被称之为nonstationary,计算R时就需要采用其他的算法了。例如,如果随着时间的推移,给出高奖励\(R\)越来越小,新的R和旧的R差距就很大了,计算R时就需要对老的奖励赋予更小的权重,这就是exponential recency weighted average(ERWA) 算法。还是之前的例子,ERWA计算出来R分别为\(R_1=ema_\alpha(S_1)=3.0625,R_2=ema_\alpha(S_2)=2.5625(\alpha=0.5)\),因此greedy动作是下一次拉动1号赌博机的拉杆。
2. 三个贡献
-
提出启发式分支算法设计的通用原则,目标是要最大化
learning rate (LR),该值表示一个变元被赋值之后产生学习子句倾向性的数值特征。- 设\(I\)为某个变元\(v\)从赋值到赋值被取消的这段间隔时间
- 设\(P(v,I)\)为变元\(v\)在\(I\)这段时间内参与生成学习子句的数量
- 设\(L(I)\)为在\(I\)这段时间内生成的学习子句的总共的数量
则变元\(v\)的LR值为\(P(v,I) \over L(I)\)
例如,有一个变元\(v\)在产生第100个学习子句产生后被赋值,参与了第101个和第104个学习子句的生成,并且在第105个学习子句产生之后赋值被取消,在这里\(P(v,I)=2,L(I)=5\),变元\(v\)的LR值为\(\frac 25\)。
注意:1. 变元v的LR值的计算具有滞后性,即分支之后并不能立即算得LR值,而是需要等到该变元的赋值被取消时才能够被计算出。2. LR值计算出来后并不是不变的,由于学习子句的删除等操作,P和L值在变化,LR值也会随之改变。
-
将变元选择的问题抽象成多臂赌博机(multi-armed bandit(MAB))框架下的问题。在这里agent是branching heuristic,action是从自由变元中挑选一个变元作为决策变元,reward是LR,value是使累计的LR最大化。
- 由于action只能从自由变元中进行挑选,所以会强制导致
exploration。 - 由于挑选一个决策变元被赋值之后,单子句传播可能会导致一连串的变元被赋值,在单子句传播过程中被赋值的变元也会被更新其LR值,这也会导致
exploration,使得R靠后的变元也有机会被选择成为分支变元。
- 由于action只能从自由变元中进行挑选,所以会强制导致
-
提出LRB启发式分支策略,该策略基于 exponential recency weighted average(ERWA)的MAB算法。并且通过 reason side rate(RSR)和 locality 拓展了纯ERWA算法,使得可以进一步最大化value。
LRB策略具体步骤:- 为每个变元都维持一个时间序列\(ts_v\)
- 当变元\(v\)的赋值被取消时,计算它的LR值\(r\),并更新其时间序列\(ts_v \leftarrow append(ts_v,r)\)和\(Q_v=ema\alpha(ts_v)=(1-\alpha)*Q_v+\alpha*r\),其中\(Q_v\)用优先队列存储。
- 从自由变元中,挑选\(ema_\alpha(ts_v)\)值最大的变元\(v\)为决策变元。
- \(\alpha\)的初始值为0.4,每次冲突衰减\(10^{-6}\),当衰减到0.06后不再衰减。
拓展1:RSR
对于出现在学习子句中的变元的原因子句中的变元\(v\)- 设\(I\)为某个变元\(v\)从赋值到赋值被取消的这段间隔时间
- 设\(A(v,I)\)为变元\(v\)作为产生的学习子句中的变元的原因子句中的变元在\(I\)这段时间内生成学习子句的数量
- 设\(L(I)\)为在\(I\)这段时间内生成的学习子句的总共的数量
则在\(I\)这段时间内,变元\(v\)的RSR值为\(A(v,I) \over L(I)\),将该拓展加入ERWA后,其\(Q_v\)的更新方式改变为\((1-\alpha)*Q_v+\alpha*(r+{A(v,I) \over L(I)})\)
拓展2:locality
如果当前求解器正工作在CNF算例的某个社区结构里面,应继续关注这个社区,而不是探索其他的社区。假设具有LR值大的变元代表了其局部性,那我们应通过限制exploration来达到更高的LR值。 ^6dd317- 每次冲突后,对所有还未赋值的变元的\(Q_v\)乘以0.95,与VSIDS的衰减类似。
3. 伪码


4. 代码
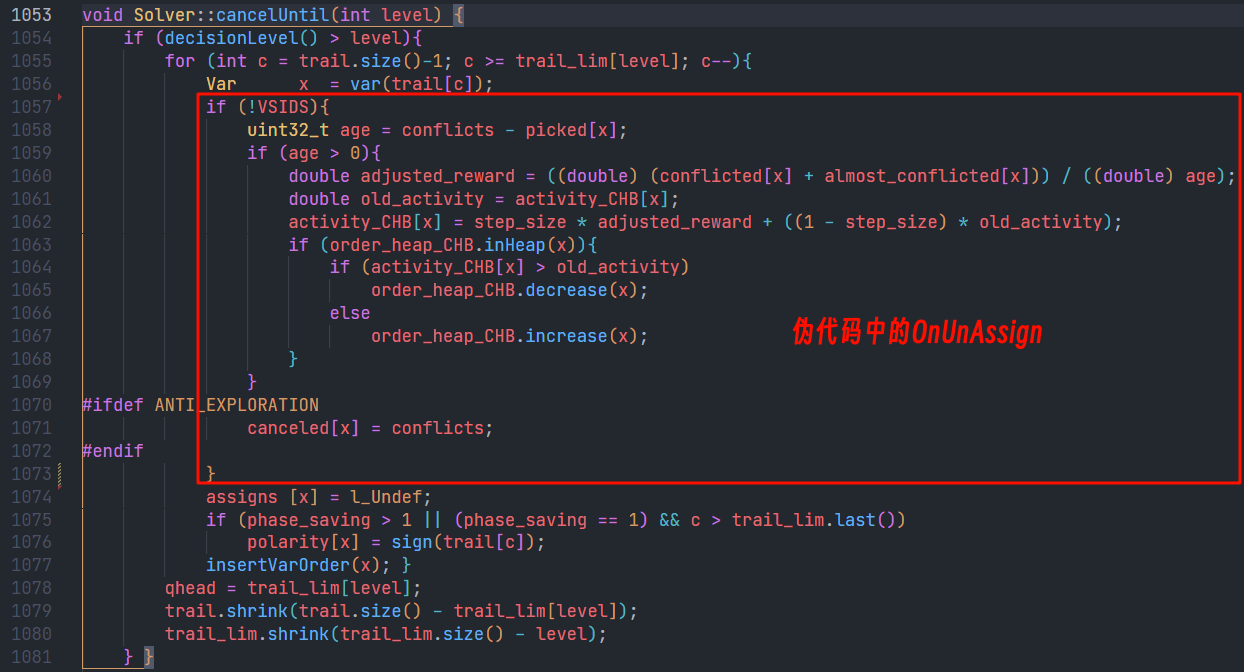


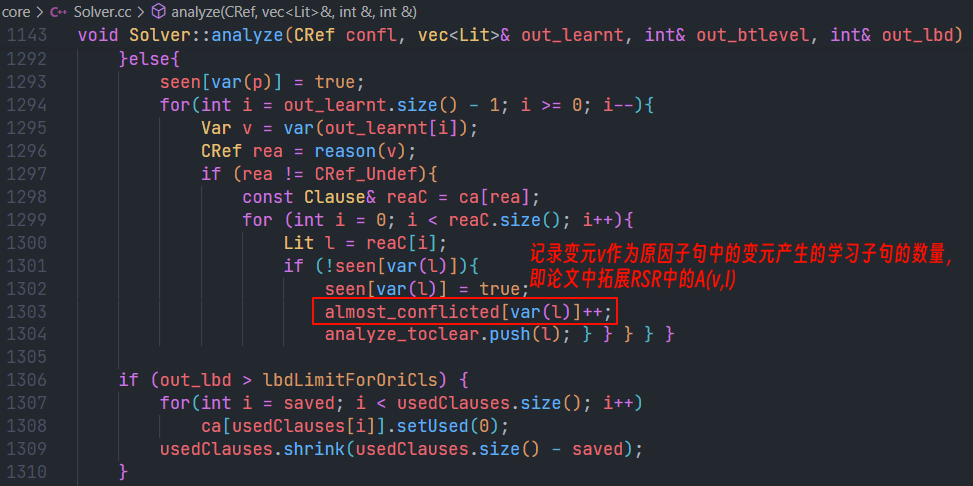
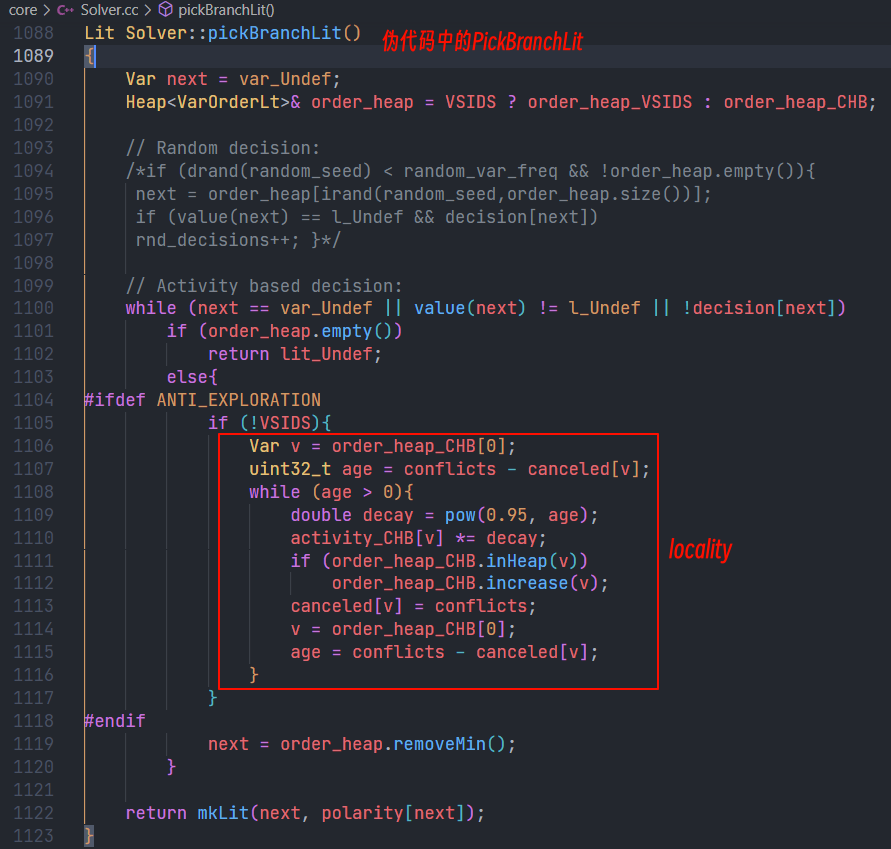
5. 结果
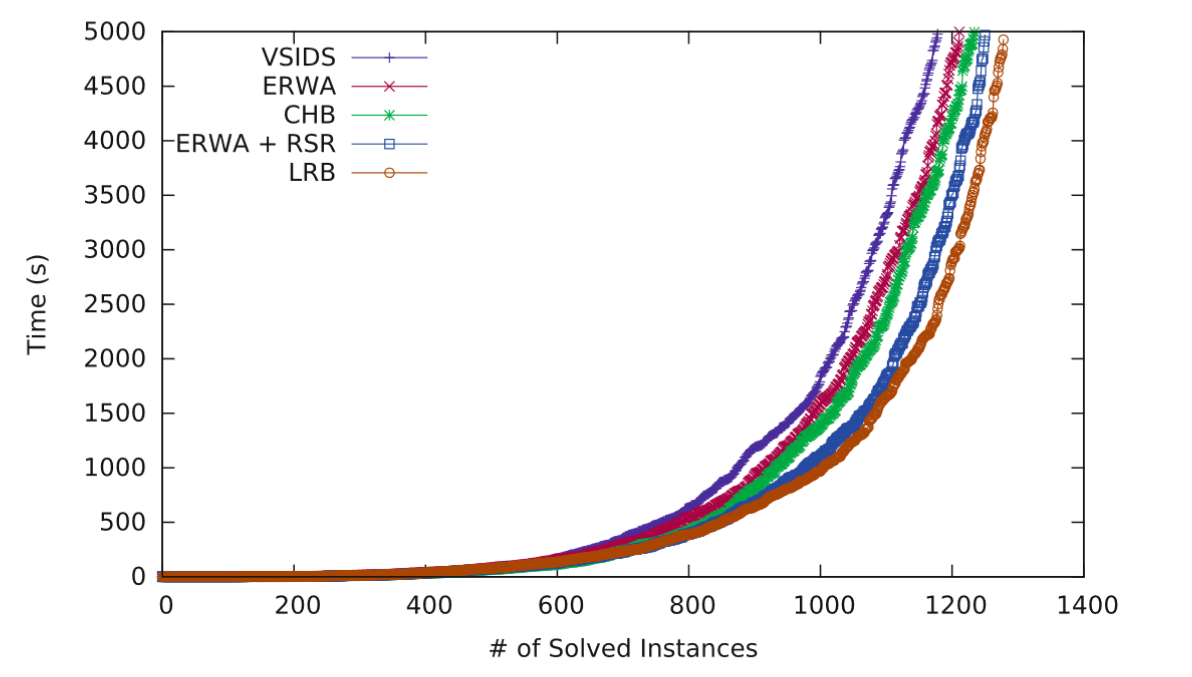
本文来自博客园,作者:seonwee,转载请注明原文链接:https://www.cnblogs.com/seonwee/p/18767204




 浙公网安备 33010602011771号
浙公网安备 33010602011771号