【题解】[蓝桥杯 2023 省 B] 景区导游

P9245 [蓝桥杯 2023 省 B] 景区导游

蒟蒻的第一篇题解，有不对的地方欢迎指正QAQ

题目传送门

P9245 [蓝桥杯 2023 省 B] 景区导游

题目省流

在给出的的一棵带边权（也就是题中的 时间 ）的树中在 $k-1$ 个点走 $k$ 次，求第 $i$ 次时经过的所有边权和

分析题目

以下是根据样例建的树
点上的数字代表 点的编号

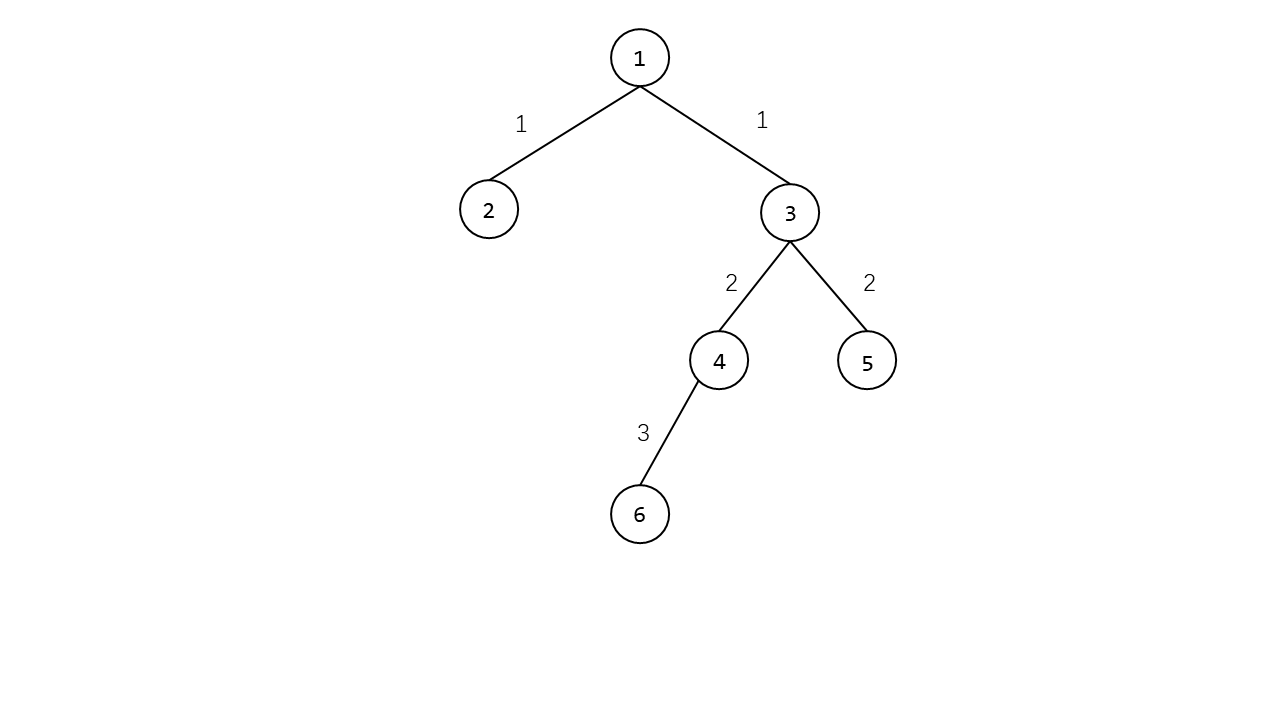
假设要从 $6$ 号点到 $5$ 号点
路径应该是 6 -> 4 -> 3 -> 5
时间和则是 3 + 2 + 2 = 7

容易想到，如果用前缀和维护该树，如图
点上的数字代表 ( 点的编号 , 从根到该点的边权和(时间) )

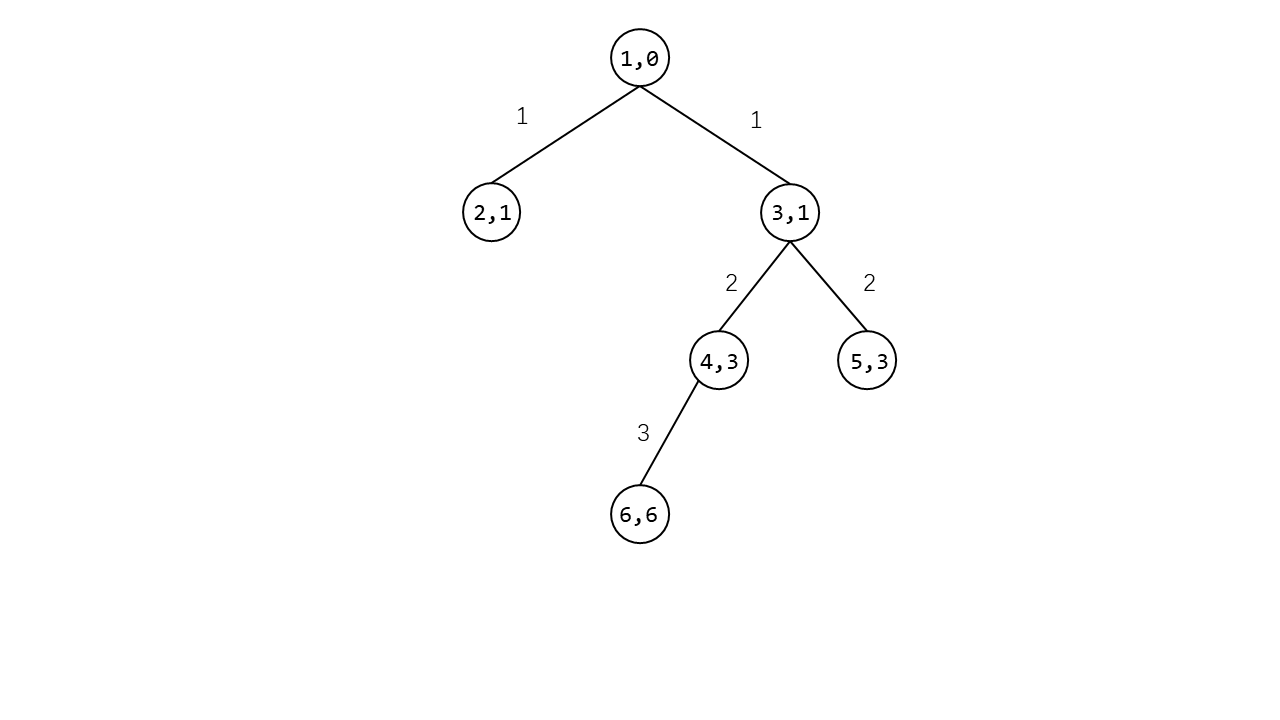
若 $time[i]$ 代表从根节点到 $i$ 节点的时间和
那么从 $6$ 号点到 $5$ 号点的时间和可以很方便的用

time[6]-time[3]+time[5]-time[3]
= time[6]+time[5]-2*time[3]
= 6 + 3 - 2 * 1
= 7

表示

那么 $3$ 号点是什么呢，就是 $5$ 号点和 $6$ 号点的 最近公共祖先
若用 LCA(i,j) 表示 $i$ 节点和 $j$ 节点的 最近公共祖先，则从 $i$ 节点到 $j$ 节点的时间和为

time[i]+time[j]-2*time[LCA(i,j)]

于是，我们可以使用 前缀和 & 倍增求LCA 求出完整线路(经过 $k$ 个点)的时间和

最后遍历一遍跳过的景点(设为第 $i$ 个点)，用总时间减去 $i-1$ 点到 $i$ 点和 $i$ 点到 $i+1$ 点的时间并加上 $i-1$ 到 $i+1$ 的时间

好长啊听不懂
没事 上图！

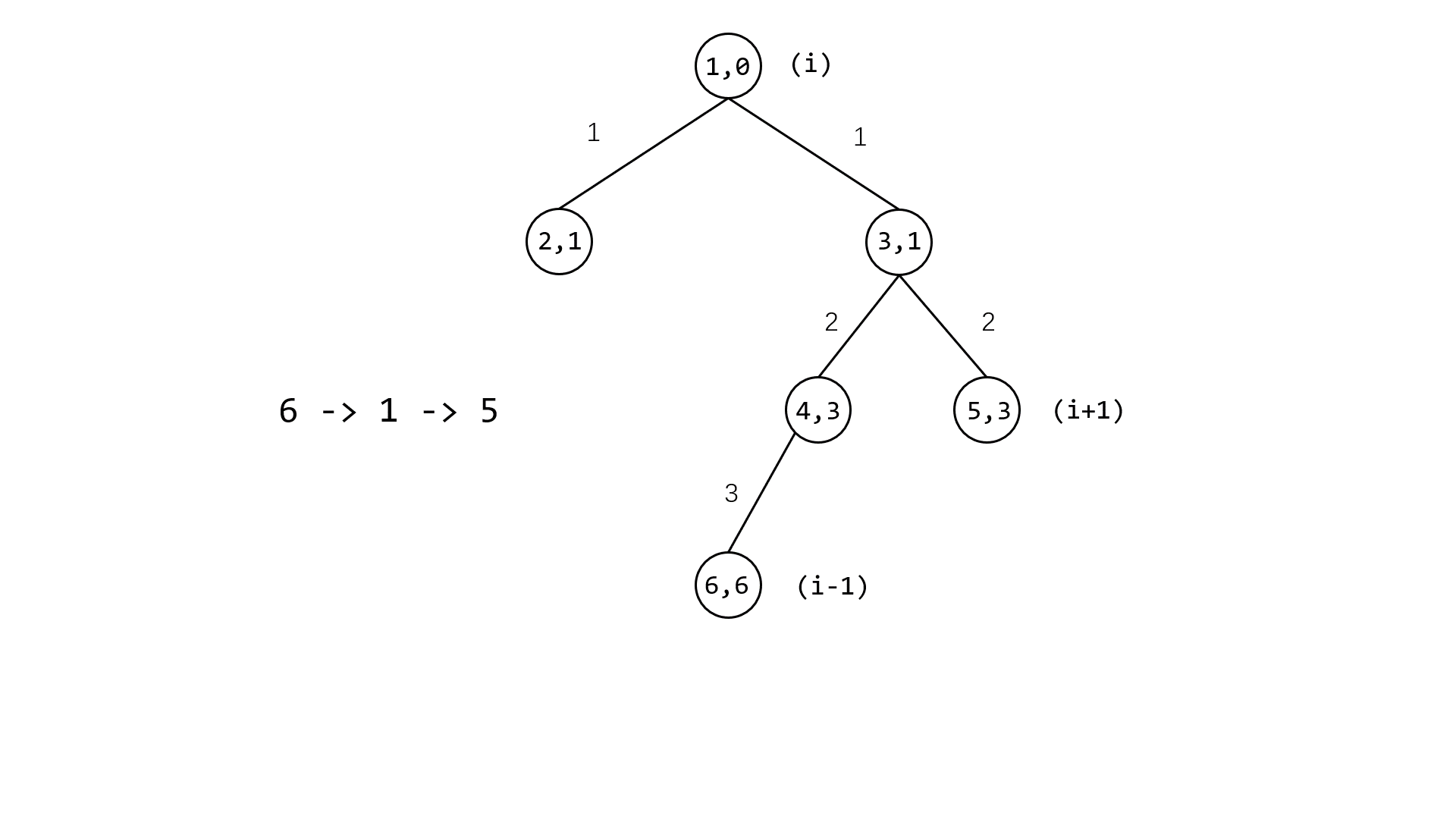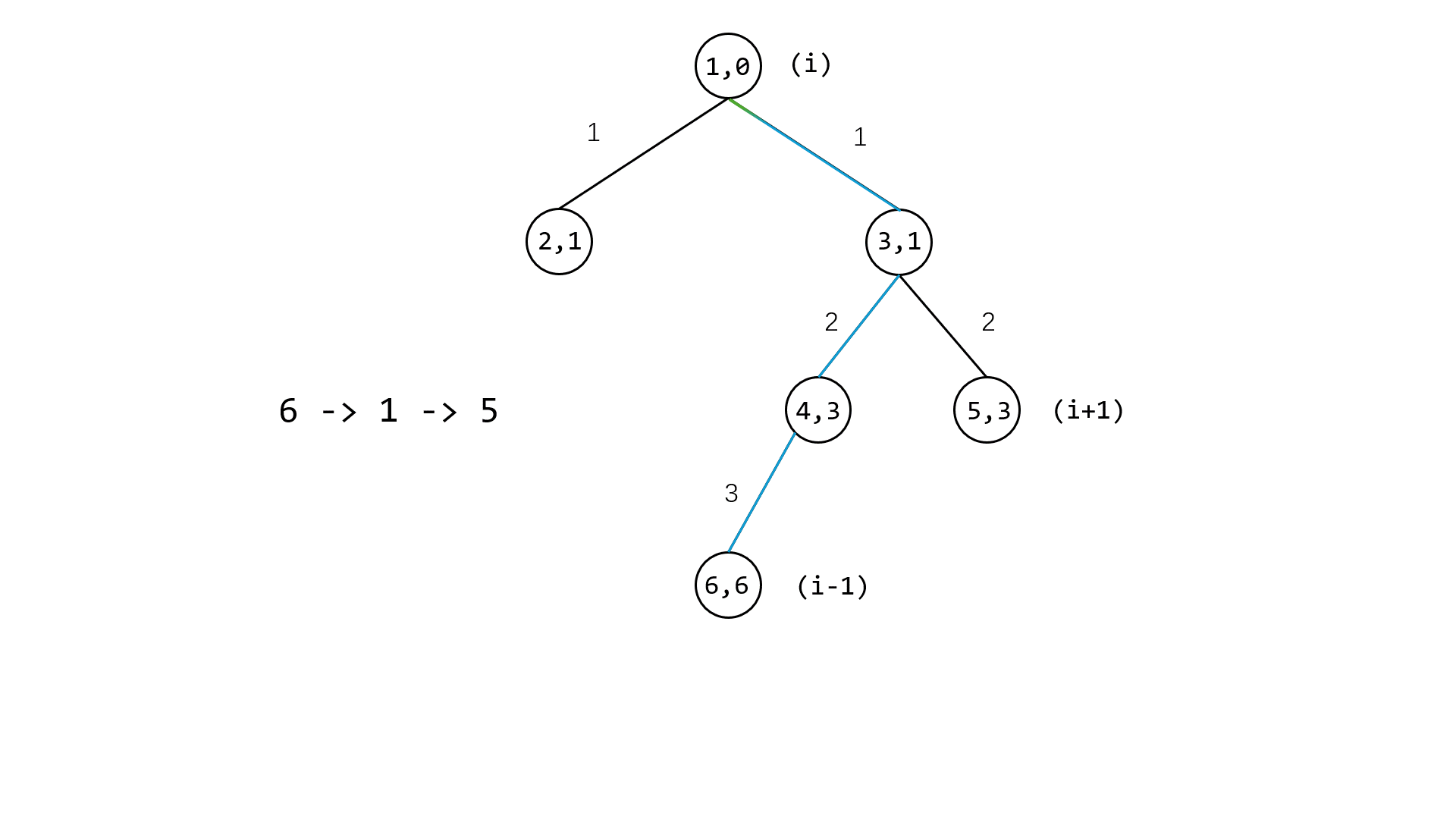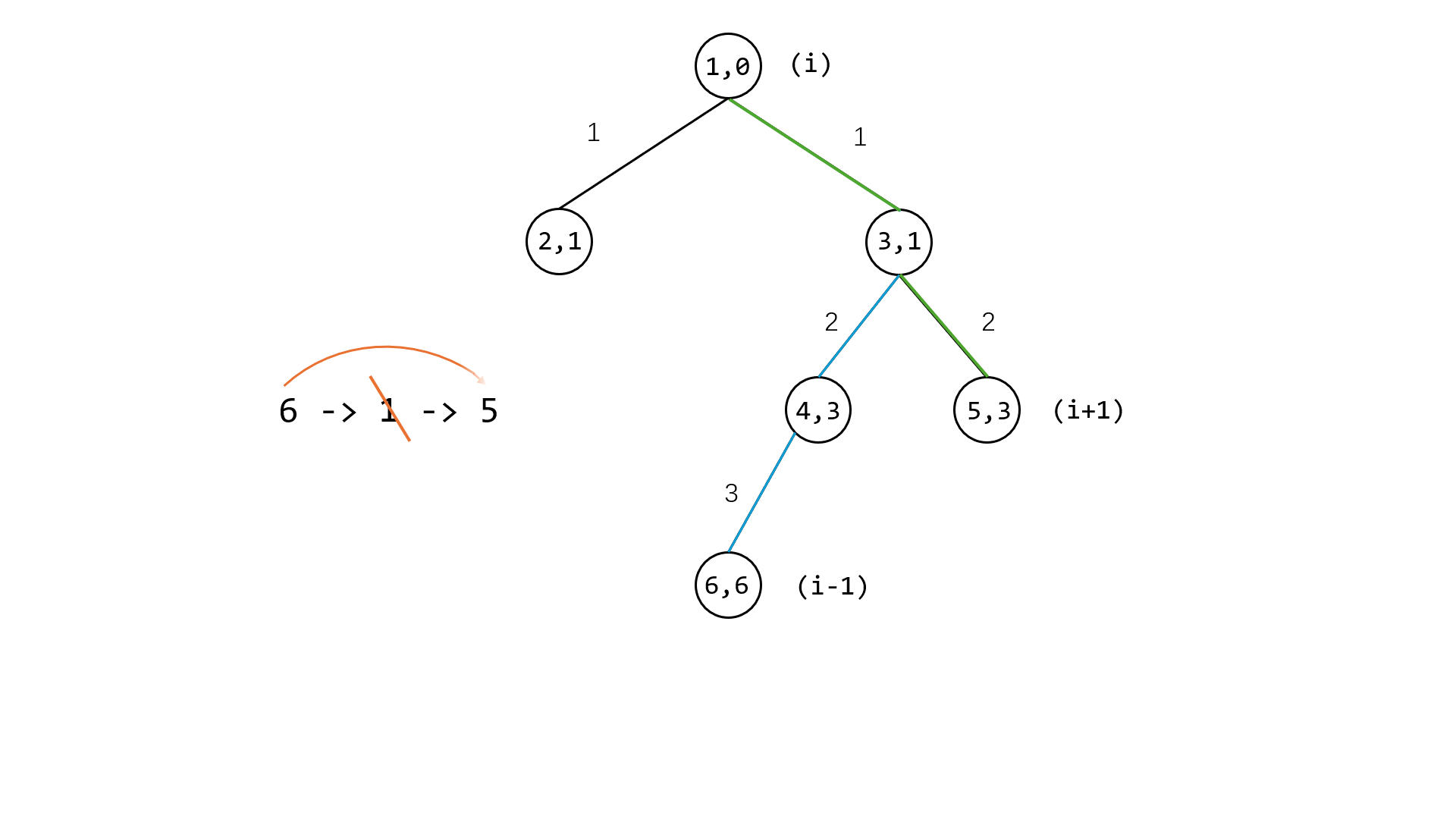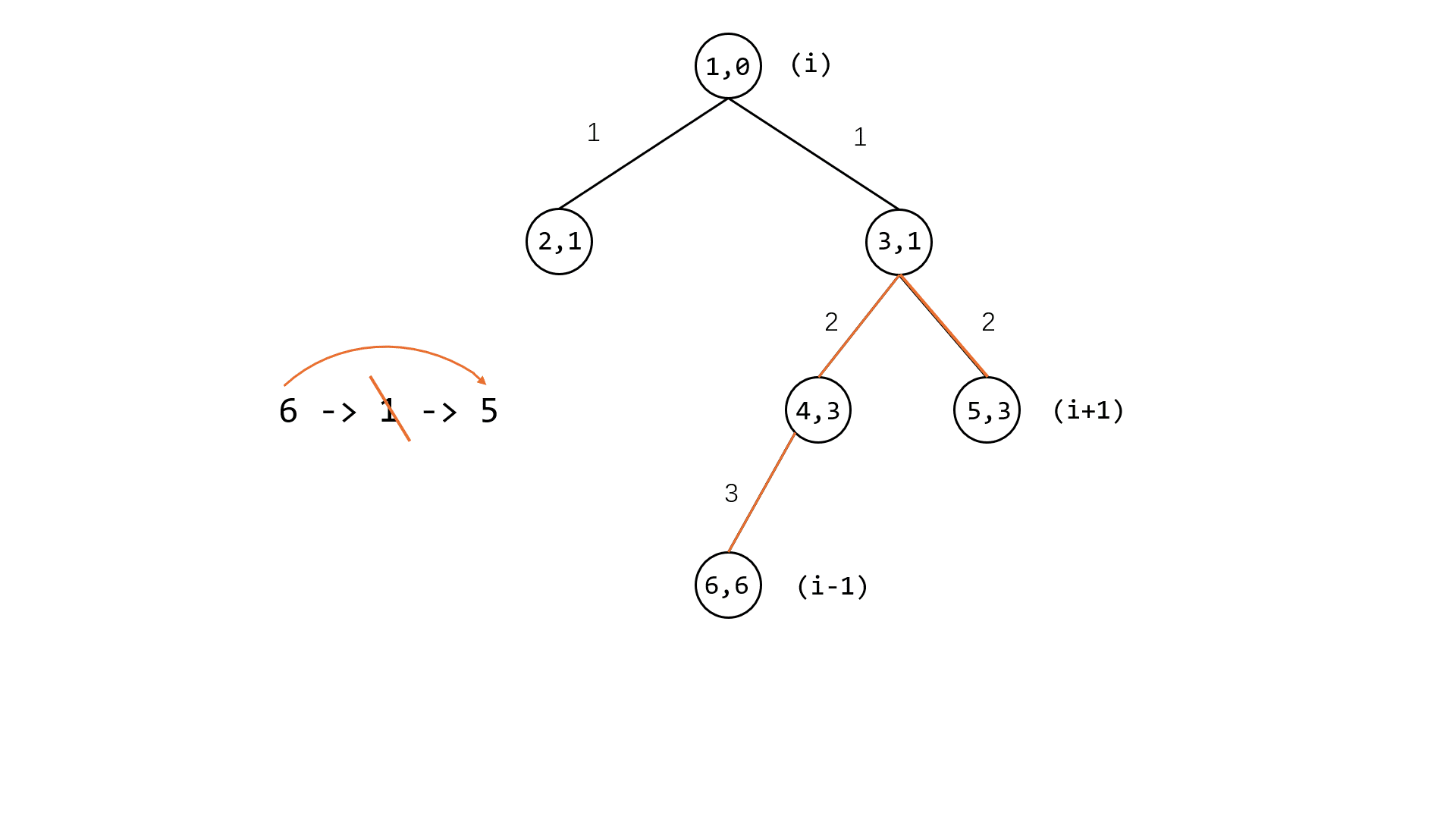
LCA

LCA可以分为3个阶段

1. 上升至同一高度
2. 一起向上寻找祖先
3. 找到辣！

// 这里使用倍增求LCA
int LCA(int u,int v){

    // STEP 1
    // 将深度大的放在变量u，方便处理
    if(tree[v].depth>tree[u].depth) swap(u,v); 
    int step = tree[u].depth-tree[v].depth;
    while(step){
        // 倍增向上step层，到v的同一高度
        u = father[u][(int)log2(lowbit(step))];
        step -= lowbit(step);
    }
    if(u==v) return u;  // 特判∶v是u的祖宗，向上step层直接碰到了

    // STEP 2
    for(int i=20;i>=0;i--){
        // 倍增向上找最近公共祖先
        if(father[u][i]!=father[v][i]){
            u = father[u][i];
            v = father[v][i];
        }
    }

    // STEP 3
    return father[u][0]; // 返回最近公共祖先
}

CODE

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 100010;
struct treeNode{
    int time_,depth;
}tree[N];

// 链式前向星存边
int head[N],edge[2*N],to[2*N],next_[2*N],cnt=1;
void add(int u,int v,int w){
    edge[cnt] = w;
    to[cnt] = v;
    next_[cnt] = head[u];
    head[u] = cnt++;
}

int guide[N],father[N][21],n,k;
// guide[i] 表示原定路线中第i个景点编号，father[i][j] 表示景点i的第2^k代祖宗结点的编号
ll record[N][2];
// record[i][0] 表示第i个景点到第i+1个景点的时间和
// record[i][1] 表示第i个景点到第i+2(跳过i+1)个景点的时间和

void init(){
    // 初始化倍增数组
    for(int j=1;j<=20;j++){
        for(int i=1;i<=n;i++){
            father[i][j] = father[father[i][j-1]][j-1];
        }
    }
}

void dfs(int x,int f,int depth=1){
    // 深搜记录深度，父子关系，时间前缀和
    tree[x].depth = depth;
    for(int i=head[x];i;i=next_[i]){
        int v = to[i],t = edge[i];
        if(v==f) continue;  // 不要往回搜啊喂
        tree[v].time_ = tree[x].time_ + t;
        father[v][0] = x;
        dfs(v,x,depth+1);
    }
}

int lowbit(int x){
    return -x&x;
}

int LCA(int u,int v){
    // 将深度大的放在变量u，方便处理
    if(tree[v].depth>tree[u].depth) swap(u,v); 
    int step = tree[u].depth-tree[v].depth;
    while(step){
        // 倍增向上step层，到v的同一高度
        u = father[u][(int)log2(lowbit(step))];
        step -= lowbit(step);
    }
    if(u==v) return u;  // 特判∶v是u的祖宗，向上step层直接碰到了
    for(int i=20;i>=0;i--){
        // 倍增向上找最近公共祖先
        if(father[u][i]!=father[v][i]){
            u = father[u][i];
            v = father[v][i];
        }
    }
    return father[u][0]; // 返回最近公共祖先
}

ll getTime(){
    ll sum = 0;
    // sum用于计算原路线时间和
    for(int i=2;i<=k;i++){
        // 往第i+1个景点走的时间
        int u=guide[i-1],v=guide[i];
        int lca = LCA(u,v);
        record[i-1][0] += tree[u].time_-tree[lca].time_;
        record[i-1][0] += tree[v].time_-tree[lca].time_;
        sum += record[i-1][0];
    }
    for(int i=3;i<=k;i++){
        // 往第i+2个景点走的时间
        int u=guide[i-2],v=guide[i];
        int lca = LCA(u,v);
        record[i-2][1] += tree[u].time_-tree[lca].time_;
        record[i-2][1] += tree[v].time_-tree[lca].time_;
    }
    return sum;
}
int main(){
    cin>>n>>k;
    for(int i=1;i<n;i++){
        int u,v,t;cin>>u>>v>>t;
        add(u,v,t);
        add(v,u,t);
        // 存边!
    }
    dfs(1,0);  // 以1号点为根建树！
    init();
    for(int i=1;i<=k;i++) cin>>guide[i];
    ll sum = getTime();
    for(int i=1;i<=k;i++){
        cout<<sum-record[i-1][0]-record[i][0]+record[i-1][1]<<" ";
    }
    return 0;
}