swintrans-blog

Swin-Transformer论文阅读

@author yulin yuan

注：本博客仅作个人记录学习所用

目录

• Swin-Transformer论文阅读
  • 一、研究背景
  • 二、贡献
  • 三、网络结构
    • 1.Patch Partition + Linear embedding
    • 2.Swin Transformer Block
      • 2.1Multi-head Self-Attention（MSA)
      • 2.2 Window Multi-head Self-Attention（W-MSA)
      • 2.3 Shift Window Multi-head Self-Attention（SW-MSA)
      • 2.4Relative Position Bias
    • 3.Patch Merging
  • 四、总结

一、研究背景

​ 语义分割是指为图片中的每个像素分配语义对象类别的问题，该技术广泛应用于无人车驾驶、医疗影像分析、地理信息系统等领域。

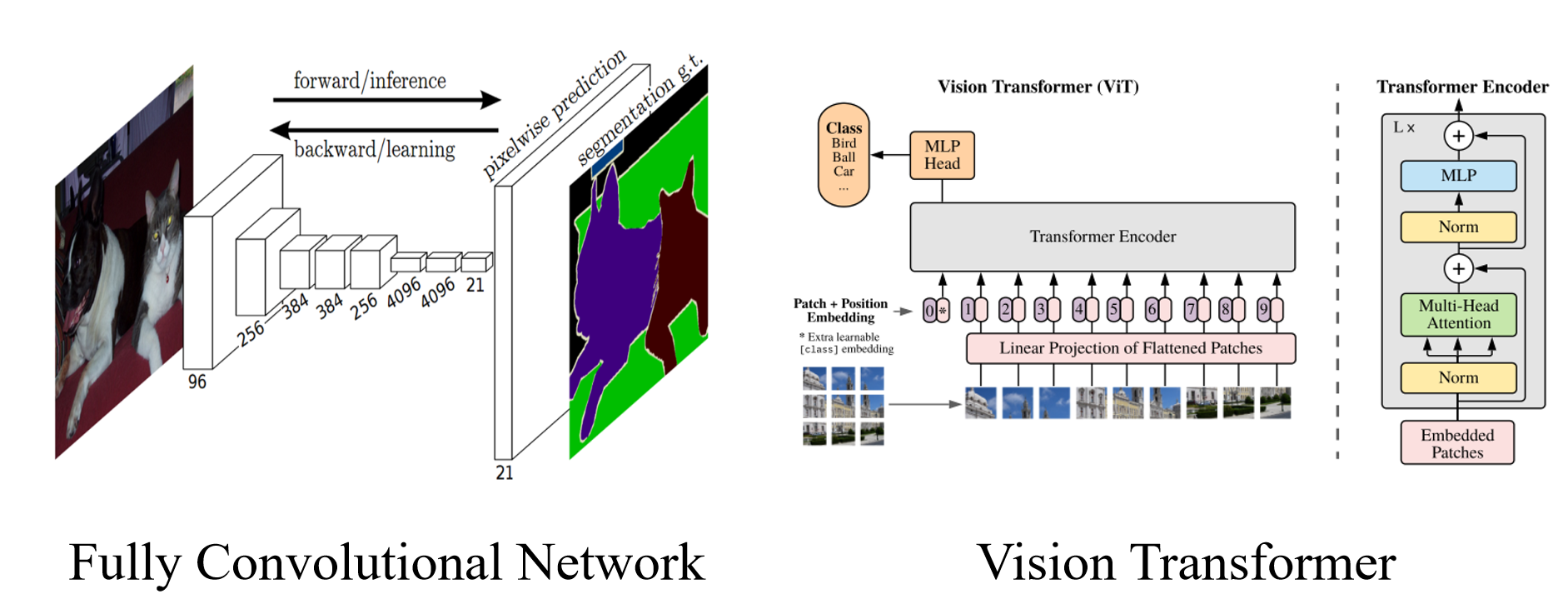
如左图所示，左边的FCN全连接卷积神经网络，仅使用全连接层，完成了对图像中的各种语义进行分割，这也是语义分割比较基础的网络。

而右图是在NLP领域的运用的transformer在CV界开出花的Vison Transformer.他也是transformer在cv界应用的基础模型。而本文的swin-transformer，也是将这两种奠基性网络上，提出的新的网络结构。

二、贡献

本文提出的网络结构是一种计算机视觉领域的通用骨干网络，它不仅可以应用于图像分类任务，同时可以应用于目标检测、语义分割等任务。

本文提出了W-MSA模块，该模块相较于传统的MSA模块，采用了多窗口结构，这一操作使得网络能够很好的关注细节信息，与此同时网络的计算量大幅减小，更有利于以语义分割为代表的密集预测任务的实施。

作者同时提出了SW-MSA这一模块，这一模块很好的解决了W-MSA模块仅在窗口内计算自注意力所导致的全局信息交流缺失的问题。

实验表明，作者的方法在图像分类、目标检测、语义分割的主流数据集上取得了最好的结果。

注：

W-MSA即 Window Multi-head Self-Attention，窗口多头自注意力机制模块。

SW-MSA即 Shift Window Multi-head Self-Attention，滑动窗口多头自注意力机制模块。

这两个模块在后面会进行着重讲解，也是本文最为核心的地方。

三、网络结构

Swin-transformer网络结构示意图如下

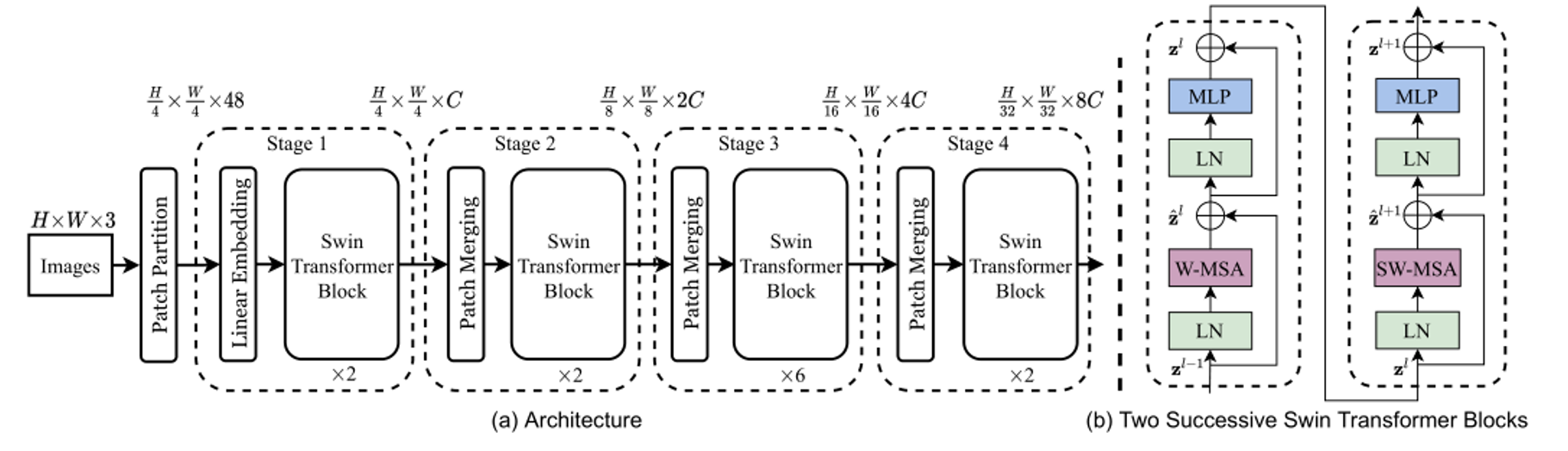
我们的原始图像，H * W *3的图片，将会以此通过以下三个重要的结构：

1.Patch Partition + Linear embedding

2.Swin Transformer Block

3.Patch Merging

最后输出一 宽度为 W/32,高度为H/32,特征维度为8C的特征图。对于语义分割来说，再给这张特征图增加一个dropout和norm层，最后用几个全连接层接收就可以得到最后的分割结果了

接下来我也会详细地介绍这三个模块，及部分的细节。

1.Patch Partition + Linear embedding

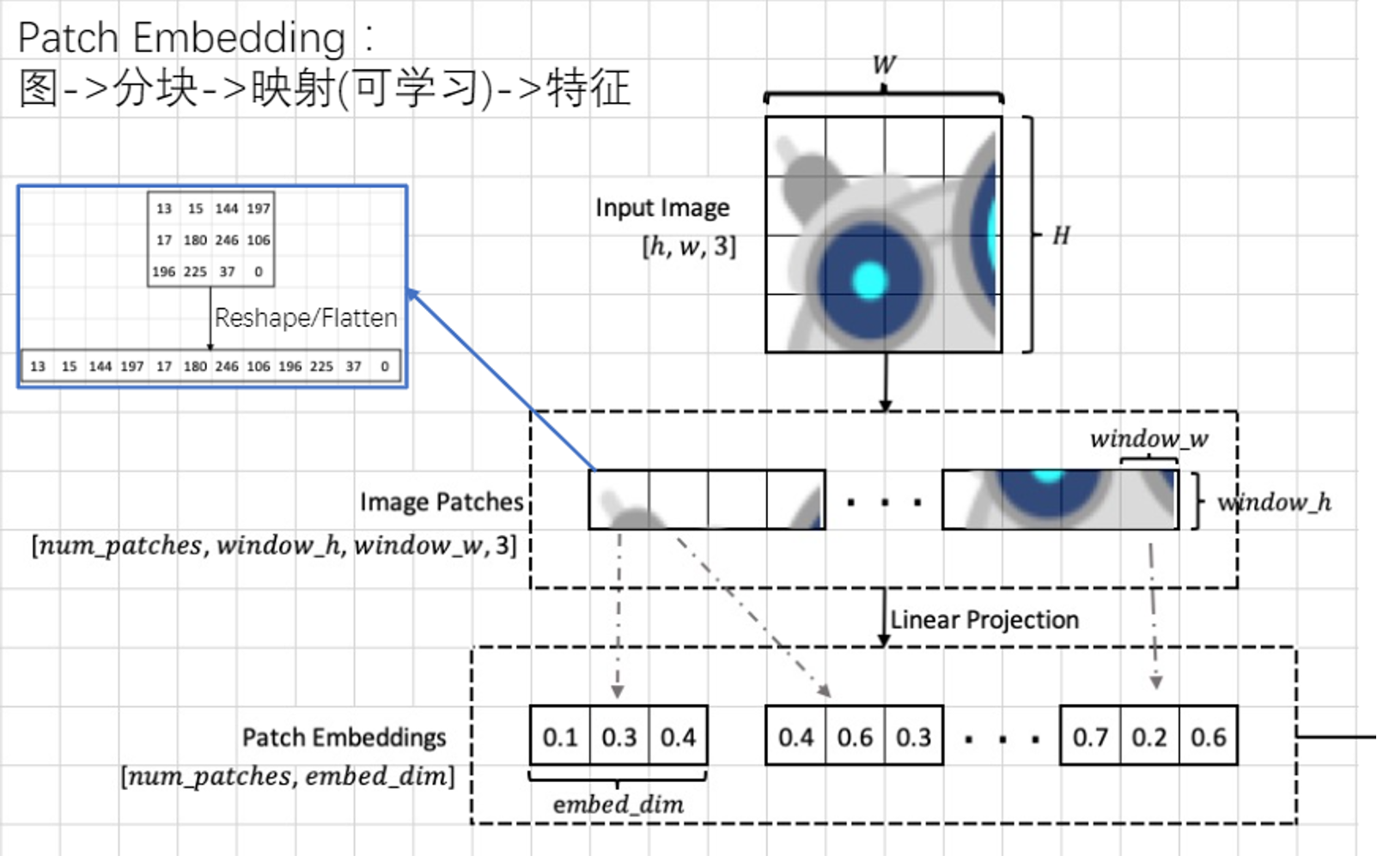
通过VIT的做法，我们可以知道，为了将attention用到cv中，需要把我们的图片类似于词向量那样编码，即将我们的图片信息转换为一定的编码，来表示词向量。因此，我们的patch partition就是这样对图片信息进行分割成一个个基本的图片信息，再将这些信息通过Linear embedding线性映射成我们的 “词向量”，以用于下一步自注意力机制的使用。

上图可以看到，我们的图片尺寸为 H * W *3,将整个图片分割为一个一个patch，作为词向量的基础。而我们这里将一个window作为图片的基本单位而非像素点，主要是方便演示。可以看到，我们这里把一个window作为一个patch，这样，我们的图片就被分为了 H * W =4 * 4 = 16个patch，同时也是16个window。关于window的概念，我们后面会有更加详细的介绍。

而对于每一个patch，他的大小为 [window_h ,window_w,3].为了方便展示，我们假设一个window 就是 2 * 2像素的大小，这样，他里面的特征经过flatten操作展平后 就是 2 * 2 * 3 =12 个。这里，就跟跟我们的词向量类似了，但是这还不够，因为他的特征维度太少了，因此我们这里对他进行一个线性映射成一个特征维度为 embed_dim的向量，而为了演示，我们这里embed_dim取3.可以看到，经过线性变换，我们最后得到的每个Patch的embedding的形状为 [num_patches, embed_dim],即patch个词向量。这样，我们的预处理工作就完成了，可以进行下一步的计算了。

2.Swin Transformer Block

在介绍这个模块的时候，我们首先需要知道他里面包含了什么。

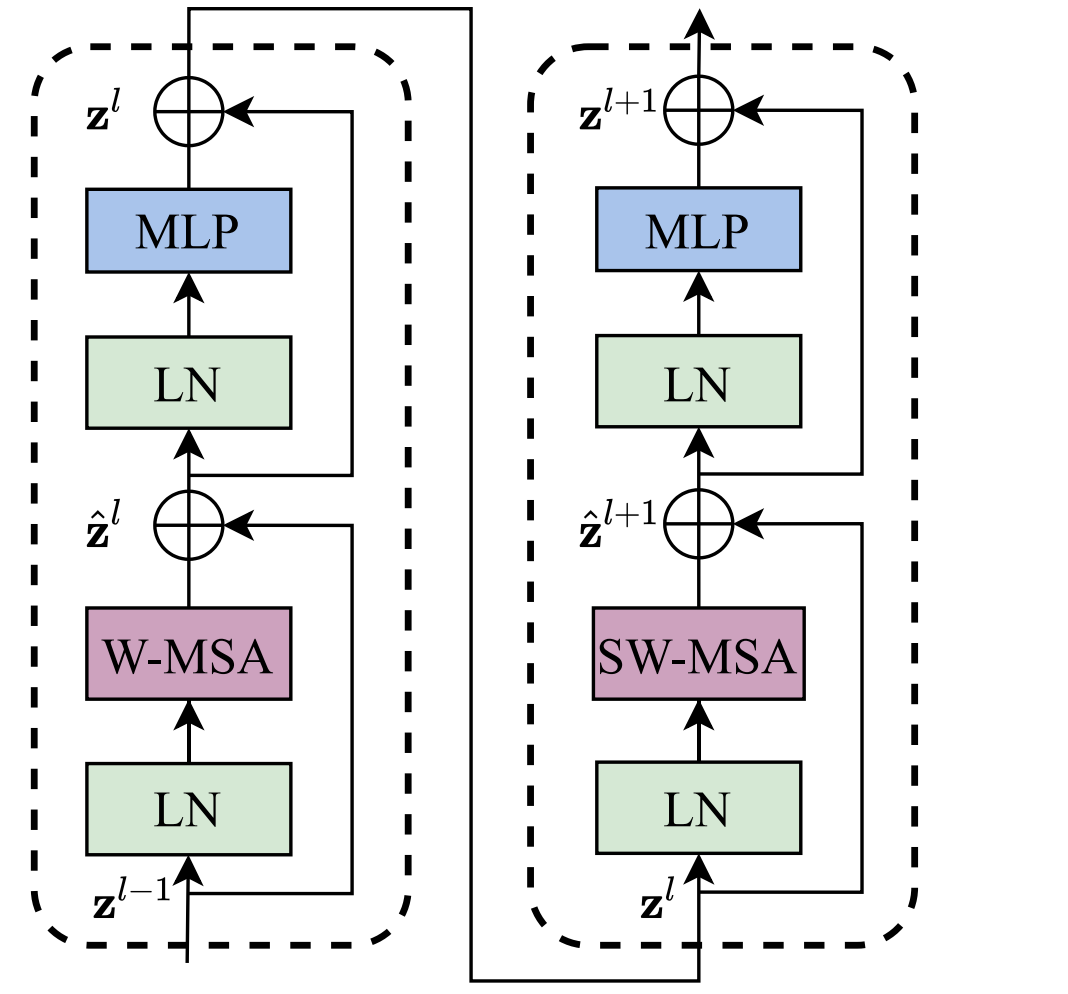
他包含了两个模块，一个是基于W-MSA的一个模块，然后他的结果进入基于SW-MSA的另外一个模块。除此这两个重要机制外，这俩模块的其他结构几乎跟VIT的一模一样，这里就不多赘述了。同时，论文还在计算attention的模块中增添了 相对位置偏移Relative Position Bias。因此，在讲这两个重要机制之前，我也会同时说明我们的MSA到底在做些什么。

2.1Multi-head Self-Attention（MSA)

即多头自注意力机制。在介绍多头注意力机制前，我先来简要介绍下我们的self-attention机制。

如图我们可以看到，这里，我们的词向量为x1，x2，x3。他的特征维度为3.我们构造了对他们共享的权重矩阵Wq，Wk，Wv来学习相关的参数，来构造我们的q，k，v。为什么要构造一个参数矩阵去学习呢？我直接用x当q，k，v不是简单省事吗？话虽如此，但我们可以想象一下，如果用这种简单粗暴的办法，两个表示相同语义的词向量直接相乘，他们的相关度一定是非常高的，但对于我们的任务来说这没有什么意义，因此我们通过采用乘上一个可学习的参数矩阵来缓和这种关系，使得相关度的表达能够更加的平缓。

我们先讲普通的self-attention机制，这里我们取x3.通过q * k的转置 来得到一组新的值s。s的数值则表示了，q和k之间的相关度，也可以理解为score，相关度得分。相信大家这里也比较熟悉了。而这里的相关度，跟我们attention机制中的权重息息相关。在论文里，通过乘上一个比例参数 1/ (dk^1/2)和通过softmax层进行一个归一化操作，得到对应的权重p，这个p就是后面我们对每个特征一个偏好程度的反映。最后再跟v向量相乘，得到了我们最终经过一定偏好权重修改后的词向量z。他相当于我们的v词向量每一个维度都乘上对应的权重，得到了最终的结果。这也就是我们的attention机制。

在回顾了注意力机制后，他存在的缺点是，他不能更加完全的捕获词向量里面特征的信息。因此，多头注意力机制的提出即解决这个问题。用mlp来说，多头注意力中的multihead，相当于里面的隐层。这样的做法，也能捕获更多的空间维度信息，提升表达能力。在我们的多头注意力机制中，即将一个词向量x的特征进行分解后，用更多的去捕获来自不同词向量相近空间位置表示更多的子空间信息。

而对比我们的attention，我们这里的多头注意力的head取3.3个head也对应我们的qkv的权重矩阵也要对应增加到3个。每个head将会关注每个词向量同一位置上的信息，同普通的注意力机制一样，最开始需要将每个词向量每个位置的特征映射到每个head中，他中间的步骤几乎不变，而最后需要将收集到的每个head的信息做一个汇总。要知道，我们的attention机制，你输入的词向量的形状和你输出的特征词向量的形状是一样的。这个形状跟我们每个head收集到的信息相同，因此，我们把所有head的信息concat起来，再乘以 一个新的参数矩阵来做一个映射，得到结果M。对应到图里面，可以看到，每个head收集的信息，就是z向量对应位置的信息，如z1的第一维，z2的第一维，z3的第一维，是第一个head关注的信息。

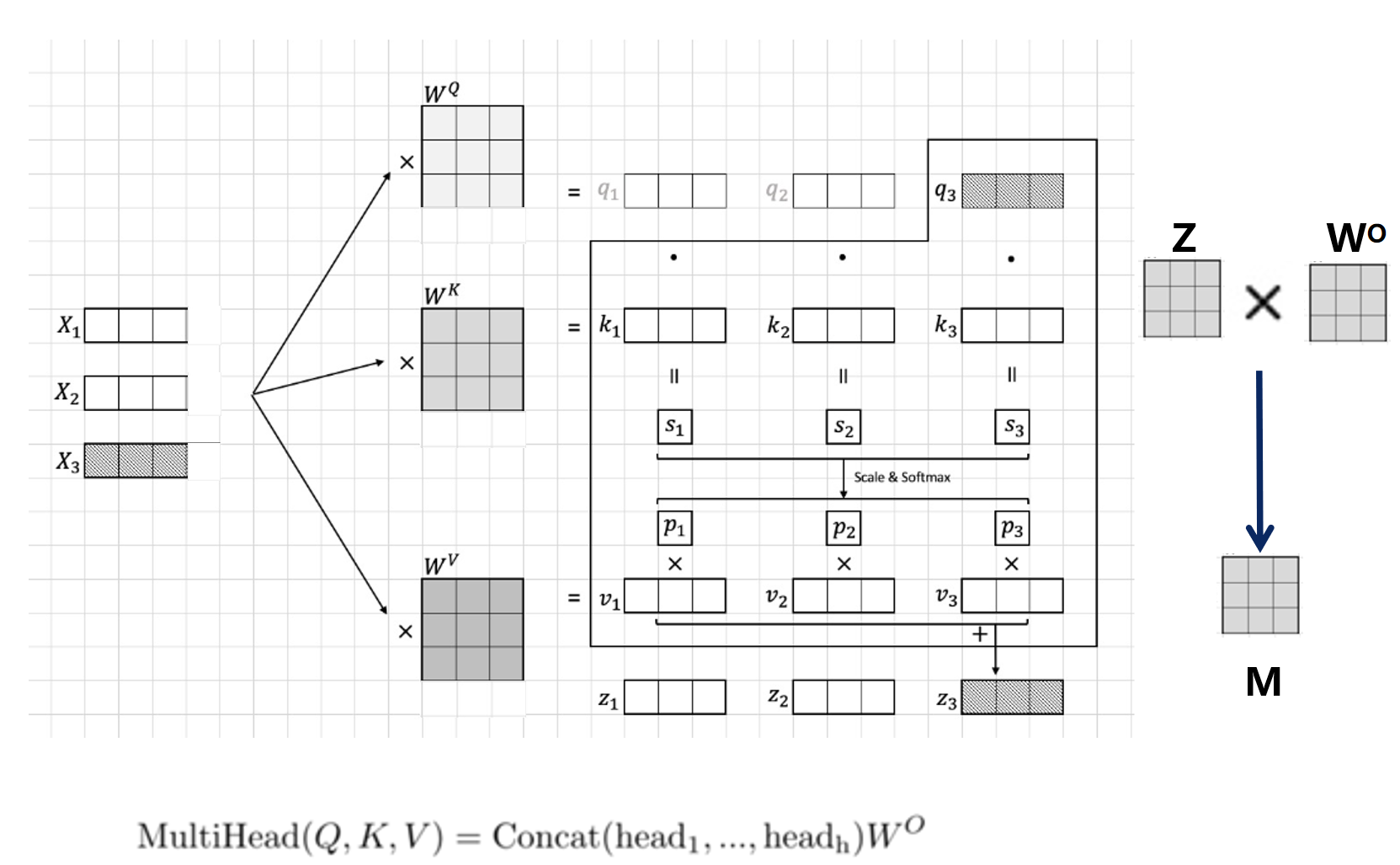
如上图所示，z1，z2，z3就是每个头得到的结果。将他们拼起来，乘以权重矩阵W得到了我们Multihead的结果M。这个M的形状和我们最初词向量X的形状是相同的。同时我们也能发现，他跟普通的attention对比，学习的参数上要比它多个W。

2.2 Window Multi-head Self-Attention（W-MSA)

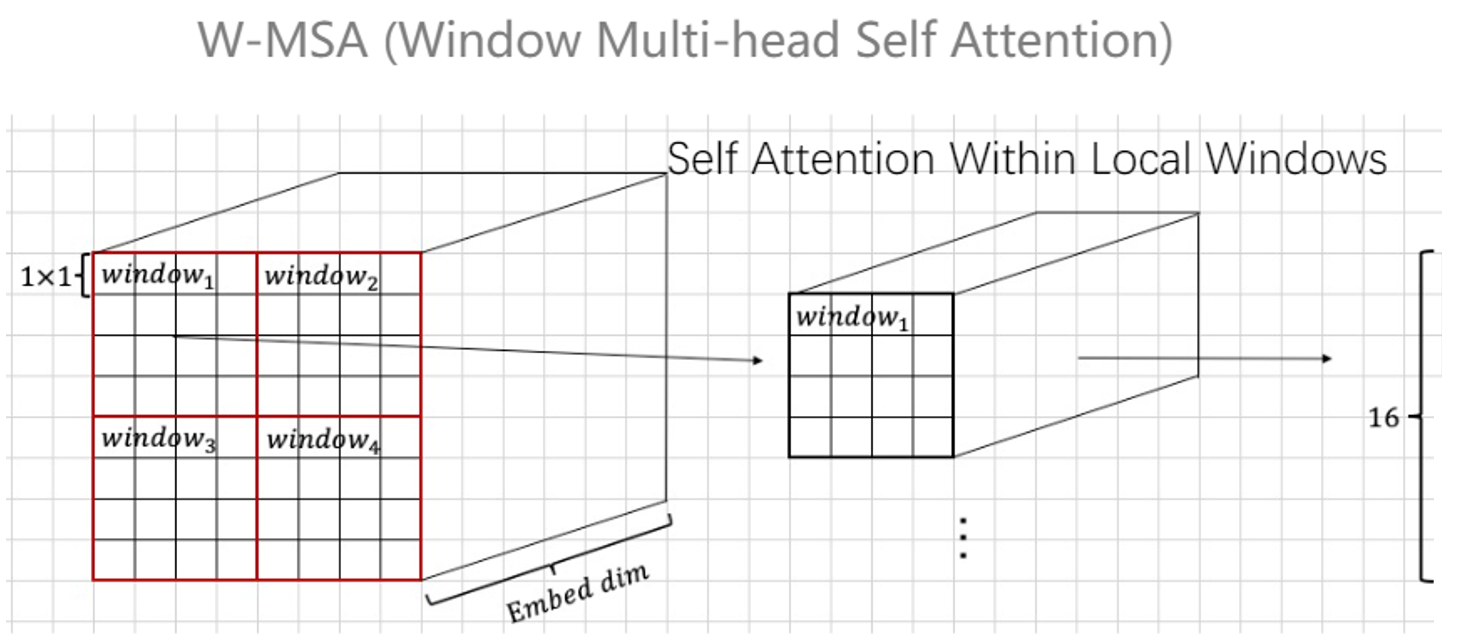
可以看到，基于窗口的MSA机制，将图片图片分为了一个一个window，使得做自注意力机制的时候，能够集中在自己的这片区域，同时可以降低参数的数量。这个操作对应CNN，跟分组卷积的原理是差不多的。那么跟普通的MSA对比，可以降低多少的参数量呢？

论文中给出了公式

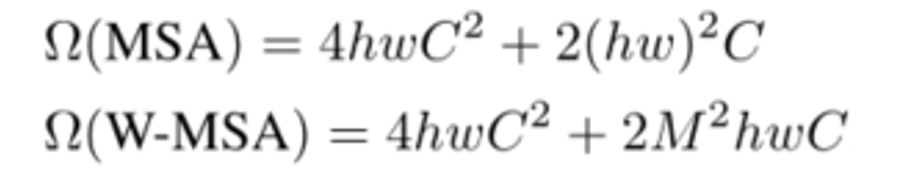
C：每一个patch的embedding后的维度

hw：输入图像被分为的patch的数量

M：每个窗口的大小

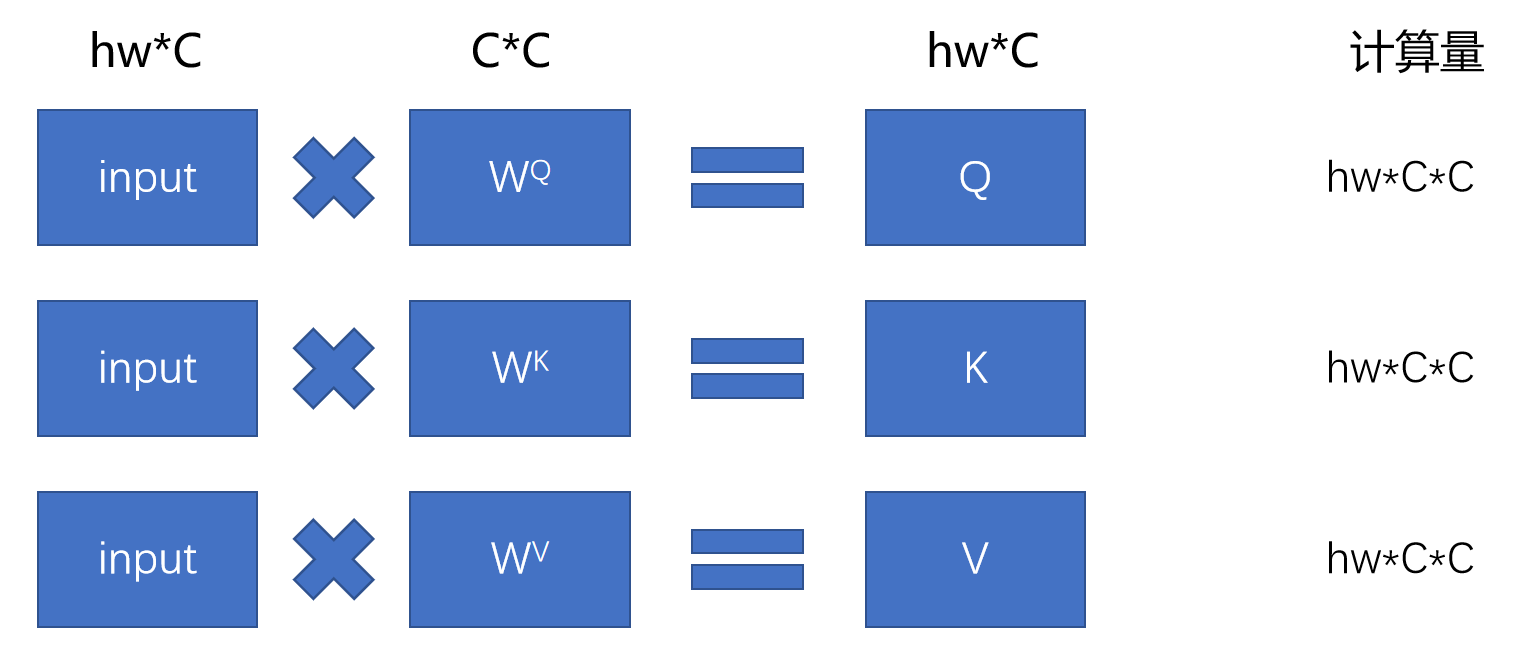
根据矩阵乘法公式我们知道，对于计算机而言，两个矩阵相乘，设他们的形状为 m * n 和 n * q，则需要三重循环遍历进行计算，故其计算量为 m * n * q。

其中，QKV的计算，需要hw*c*c+hw*c*c+hw*c*c=3hw*c*c的参数。

现定义**d**为每一个头中的patch的embedding后的维度，则c/d为头的个数。

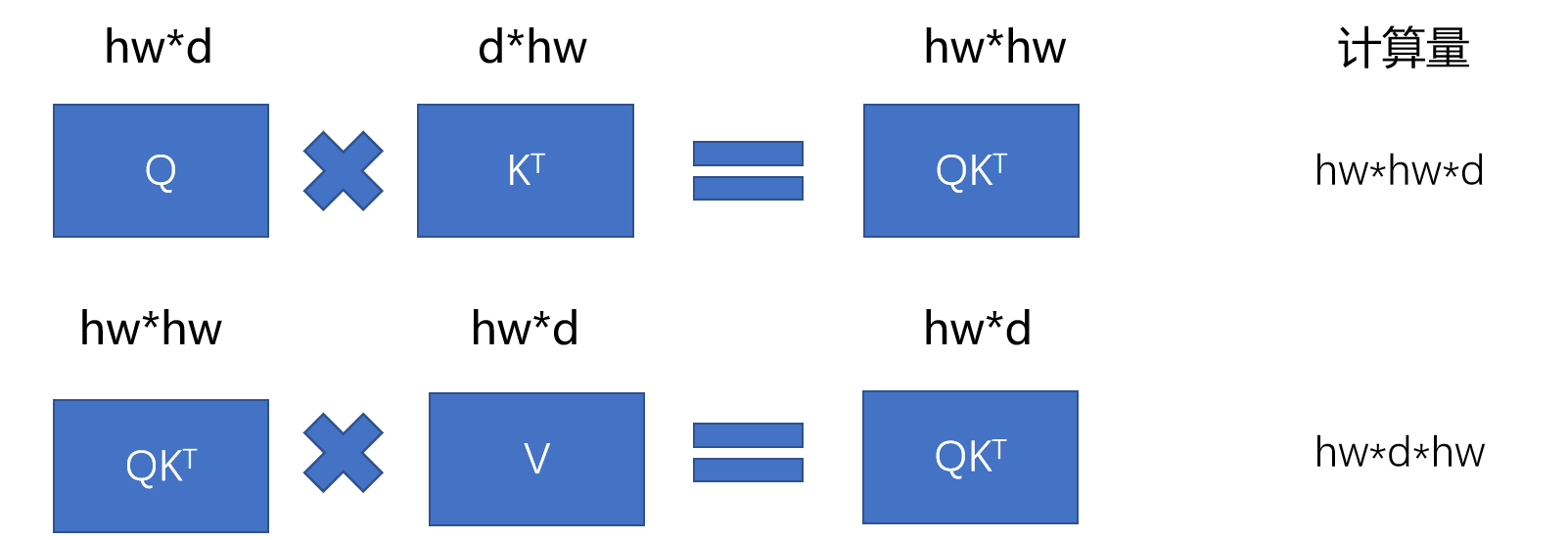
Q * K ， QK * v所需要的参数为 2c（hw）^2.

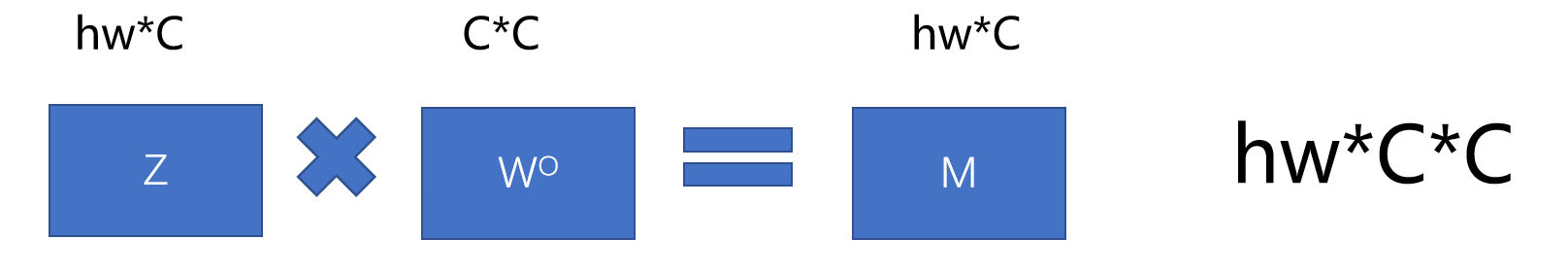
再加上多头最后需要汇总，还需要将Z 和W相乘，这个参数又是一个H * W * C * C。

因此MSA的总计算量为：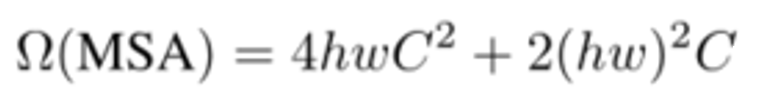

那么对于W-MSA，他的计算量公式为：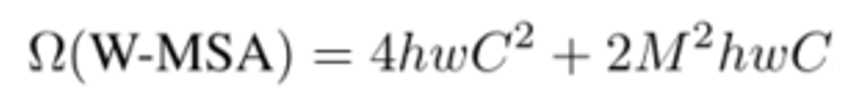

这里的定义跟上面相同，唯一不同的是，定义M为每个窗口的大小（一维）。

因此，可以计算，一张图片，一共有 h / M * w / M个窗口。

然后让一个窗口当做一张图片的hw去计算，他的参数就是窗口数 * 一个窗口的计算量。

（h / M * w / M ） * （4M^2 * C^2 + 2M ^ 4 * C）=4hwc^2 + 2M^2 * hwc.

当 h = w =56,C=96,M=7时，4hwC2计算量相同，其余部分
前者计算量为 2(5656)2 96 = 1888223232
后者计算量为 2725656*96 = 29503488

两者相减我们也可以知道，这俩者的计算量就是在比较 M* M 和 hw的大小。一般来说，M肯定比hw要小，M越小，所节省的计算量就越大。

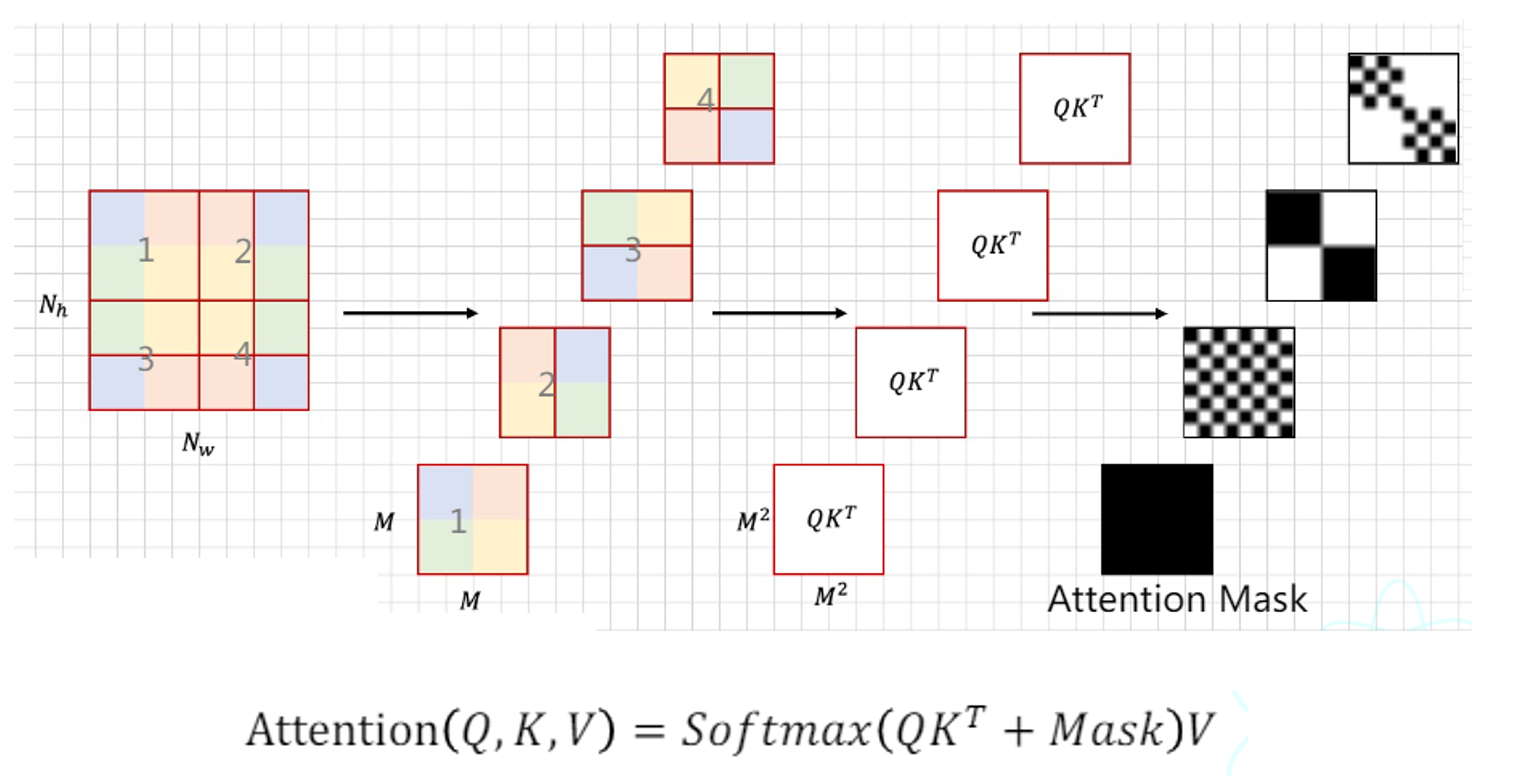
到这里，W-MSA就介绍好了，他成功的计算一个窗口内部特征之间的相似度。这也存在一个问题，即一个窗口只有本窗口相似度的信息，非常局部。因此，SW-MSA机制很好的解决了这个问题。这也是我接下来要介绍的。

2.3 Shift Window Multi-head Self-Attention（SW-MSA)

使用W-MSA的缺陷也很明显，就是每个window单独计算窗口内的信息，只在意全部而没有在意全局的相关性。因此，论文提供了一种滑动窗口机制，来解决这个问题。

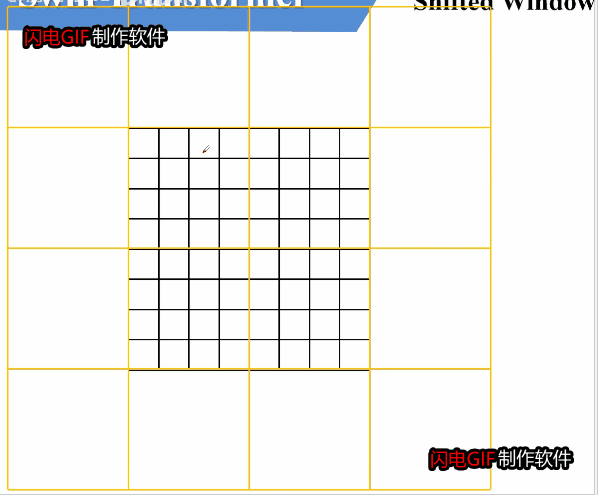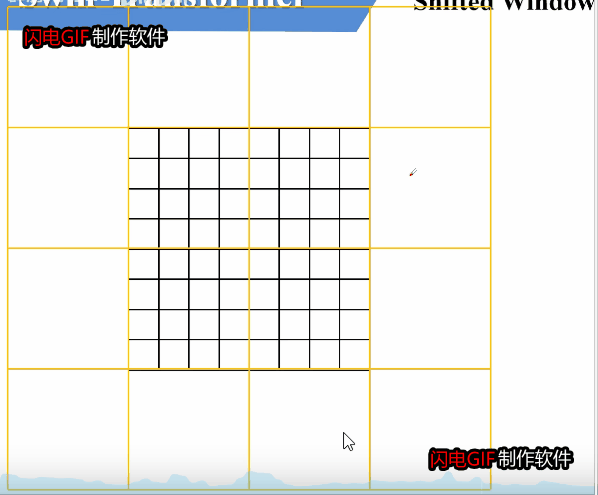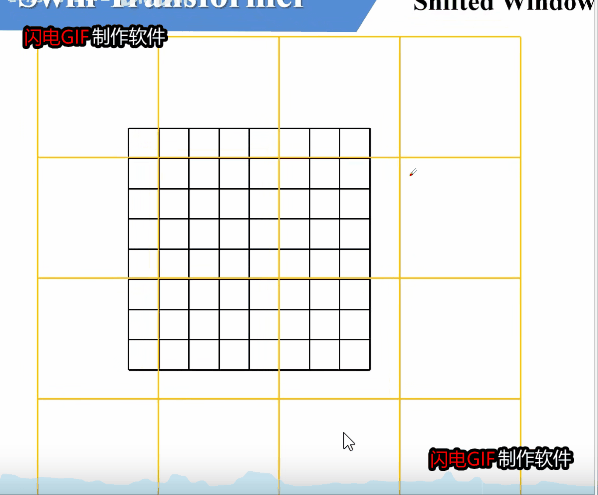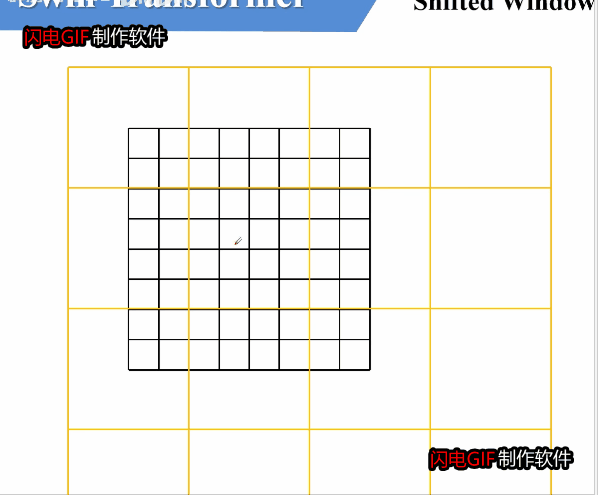
如何进行滑动呢，可以参考上面这张图。窗口整体向右下滑动了2个单位，使得其他窗口的信息能得到交换。

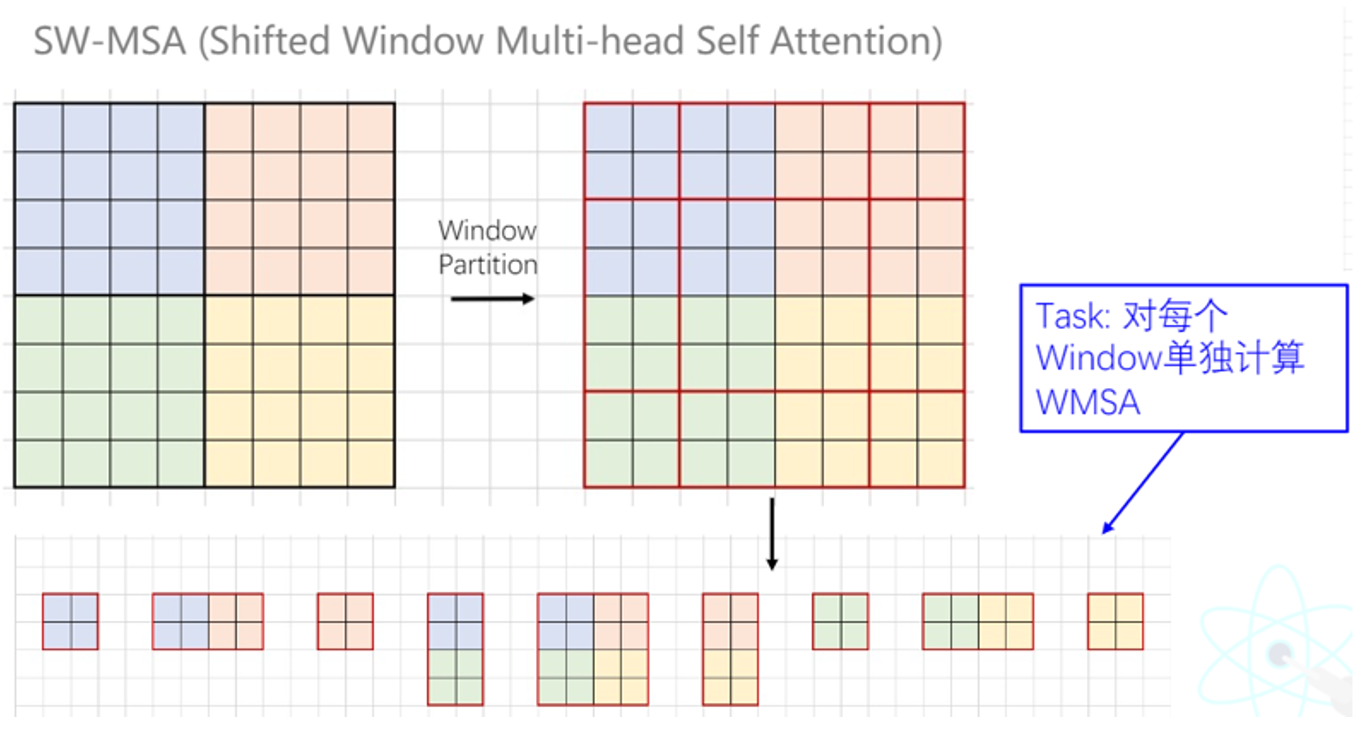
但这样滑动可能会带来问题。可以看到，滑动之后，由原来的四个窗口变成了大小不一的9个窗口，每个窗口对窗口内单独计算W-MSA。这种数量变动，大小不一的窗口，这对于继续下一步的计算是很不方便的。我们需要有9个窗口计算的效果，但是我们不希望这种效果带来的不方便存在。

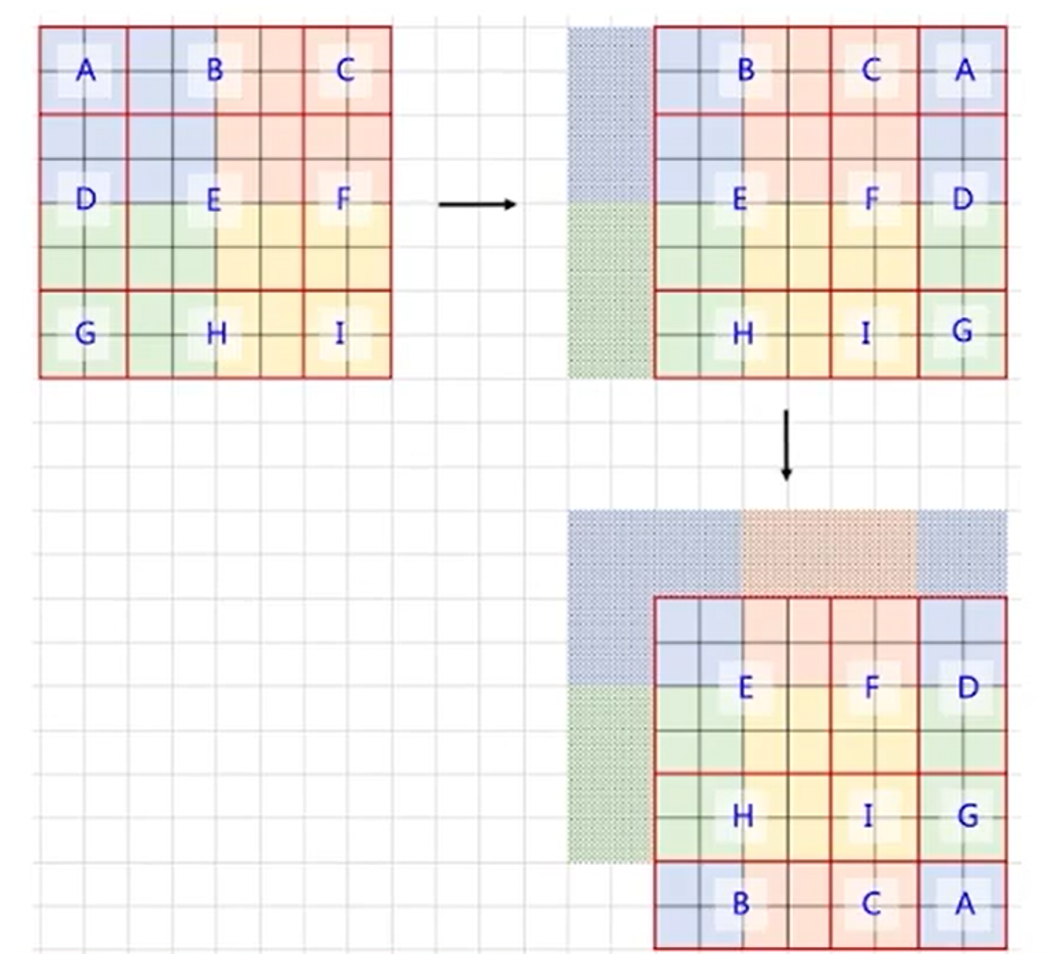
为了方便统一形式和方便计算，我们希望滑动后，窗口的大小和数量都不发生变化。论文中采用了一种方法，将ADC三个窗口移动到CFE的右侧，再将BCA移动到HIG的下方。如果设滑动的单位是x，则该操作相当于将原来的图像前x行附加到图像下侧，前x列附加到图像右侧。

从操作结果来看，E为4 * 4的窗口，F,D组成 4 * 4的窗口，H ，B也组成 4 * 4 的窗口，I,G,C,A组成 4 * 4的窗口。这比较成功的实现了我们当初的目标，即保持窗口数量大小都不变。

那么问题来了。这如何保证计算的效果一样呢？

我们希望计算的效果，显然是这9个窗口进行W-MSA的效果。而上述操作，则是4 个窗口产生的效果，将两个窗口直接拼接计算，肯定会导致窗口的独立性被破坏。

被破坏会怎么样呢？举个例子，拿D 和F来说，这两个窗口对应应该是图像边缘的信息，他们之间显然不应该产生联系，放在一个窗口内直接计算显然是不妥当的。因此，论文提出了一种窗口掩码机制。是对合并后窗口计算出来的效果，最终进行一个的掩码运算，将本来不该产生联系的部分，置为0（即毫不相干）。

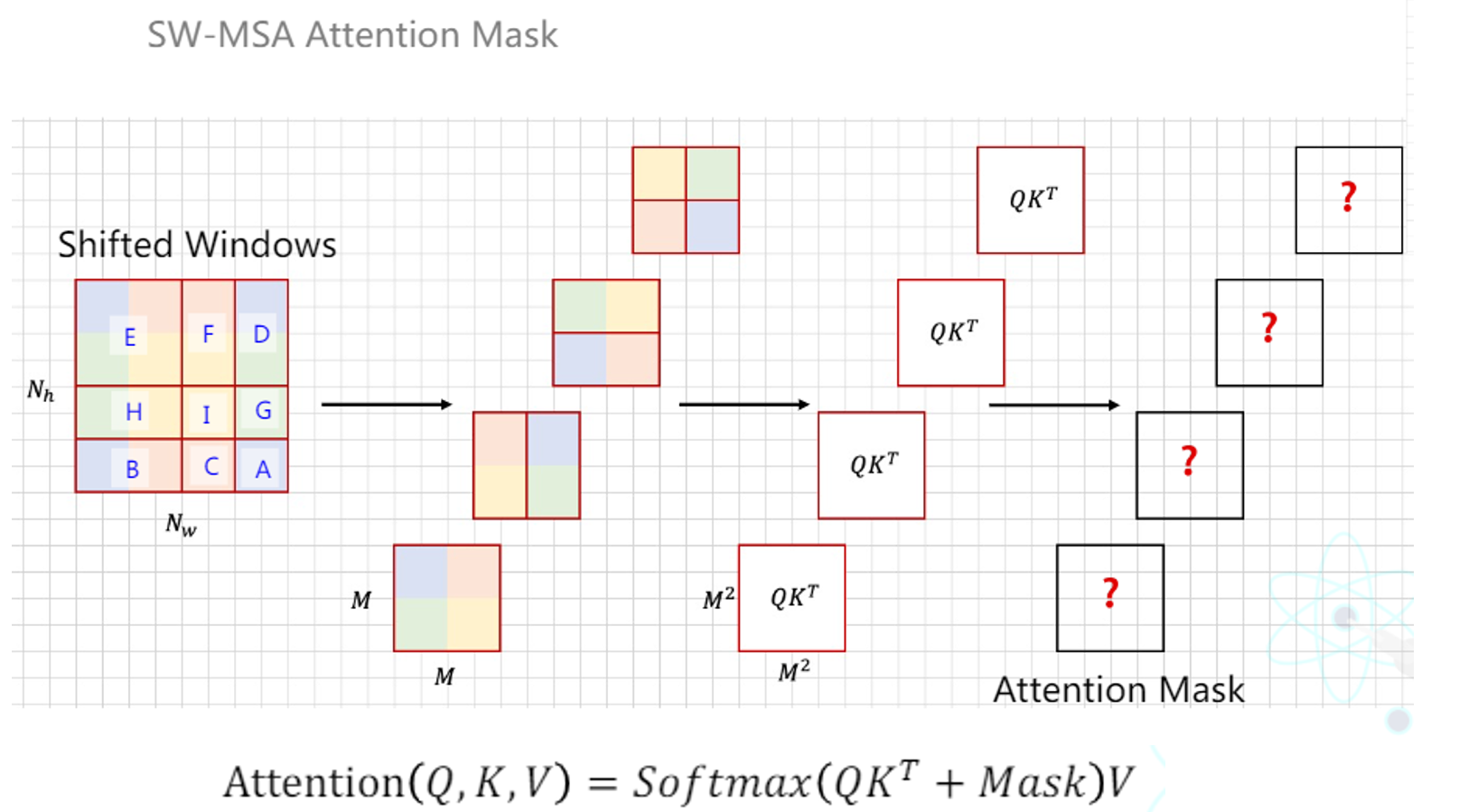
在论文中，掩码mask是在计算完成QK后，采用直接相加的做法加上去的，在我们想要掩盖的地方，其数值为-100，这也是论文的做法。为什么是-100而不是0呢？因为在经过softmax后，这个非常大的负数将会被直接削弱到趋近于0，这也达到了我们掩码的效果。但是，不同窗口，如何确定他们的掩码呢？

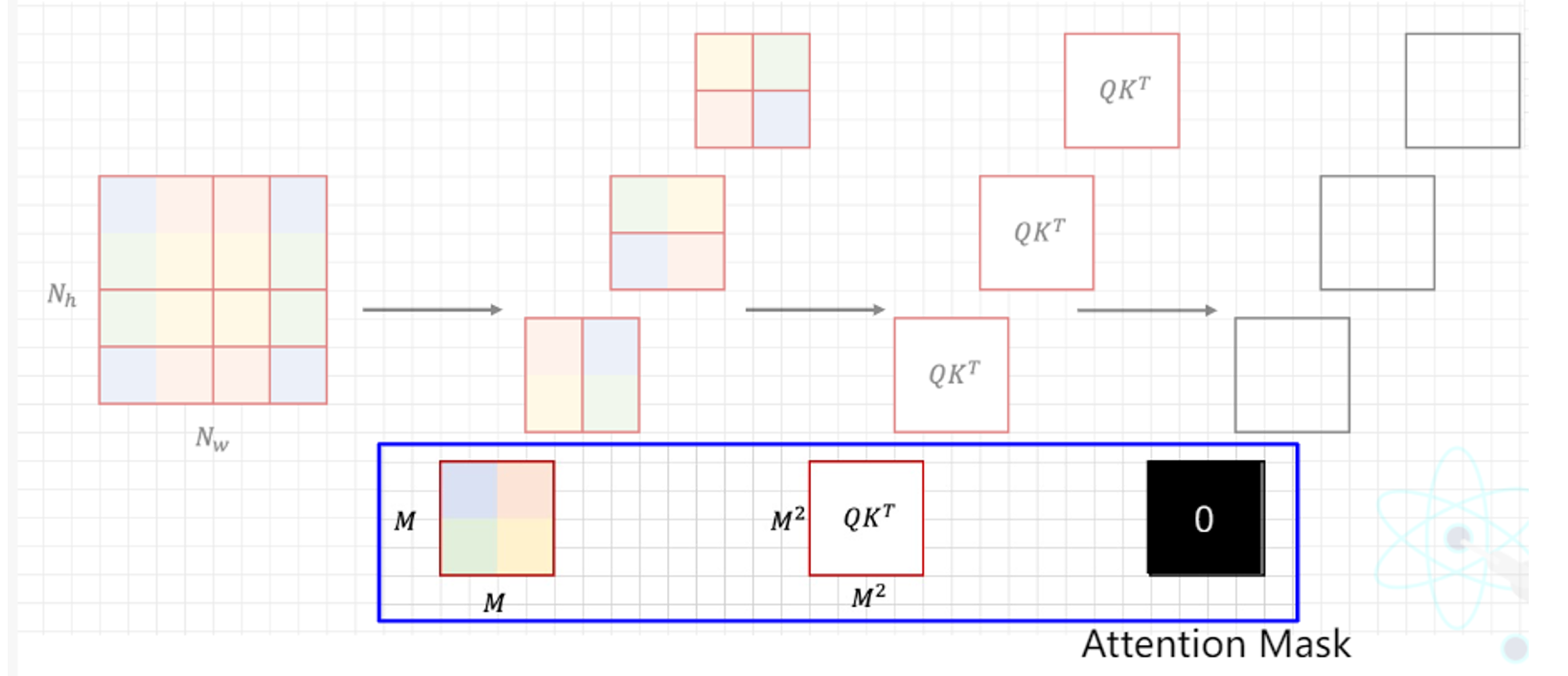
对于最底下第一个那个本身也没有经过组合的窗口来说，显然他是不需要掩码的，因此他的掩码部分全部置为0，而非-100.

需要注意，图中标注的数字0表示mask的值，0代表什么也不做，-100表示此处进行掩码。

那么对于其他窗口，不同的窗口之间掩码也是不一样的。我们先来看下这倒数第二个窗口。

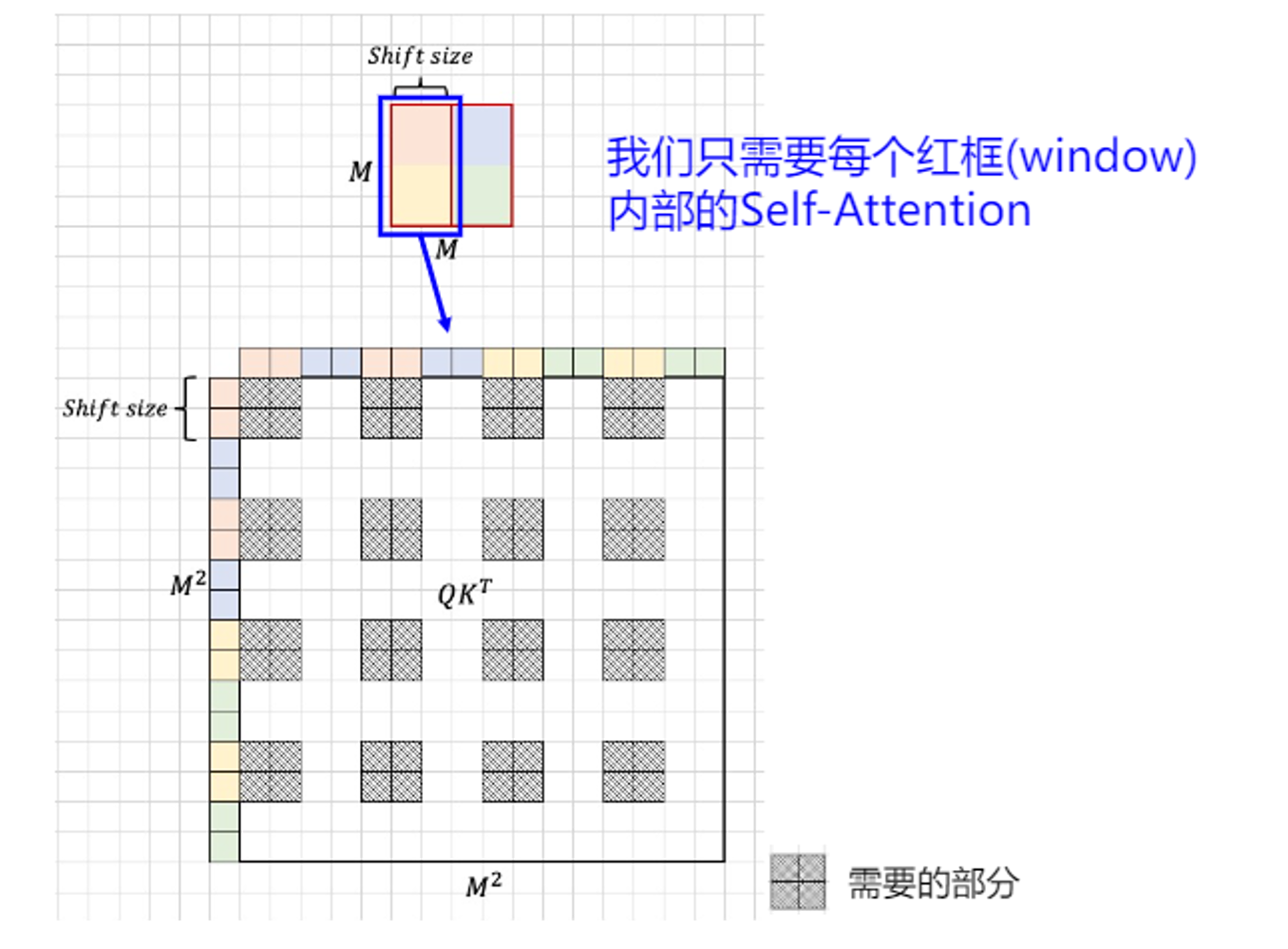
可以看到，我们事实上需要attention计算的部分，则为两个窗口分别计算部分之和。

左边的窗口，就是蓝色框标出来的部分，对应到attention中，就是阴影部分表示的区域。

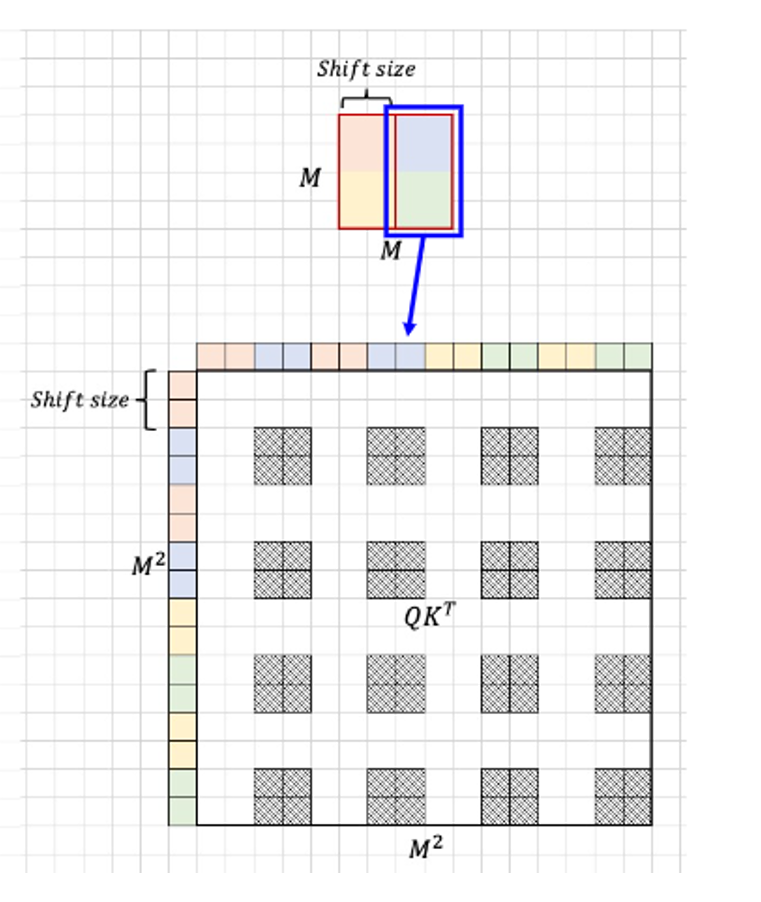
而右边的窗口，需要计算的部分也如图所示。两个窗口需要计算的部分相加，就构成了我们要给这个窗口的掩码。

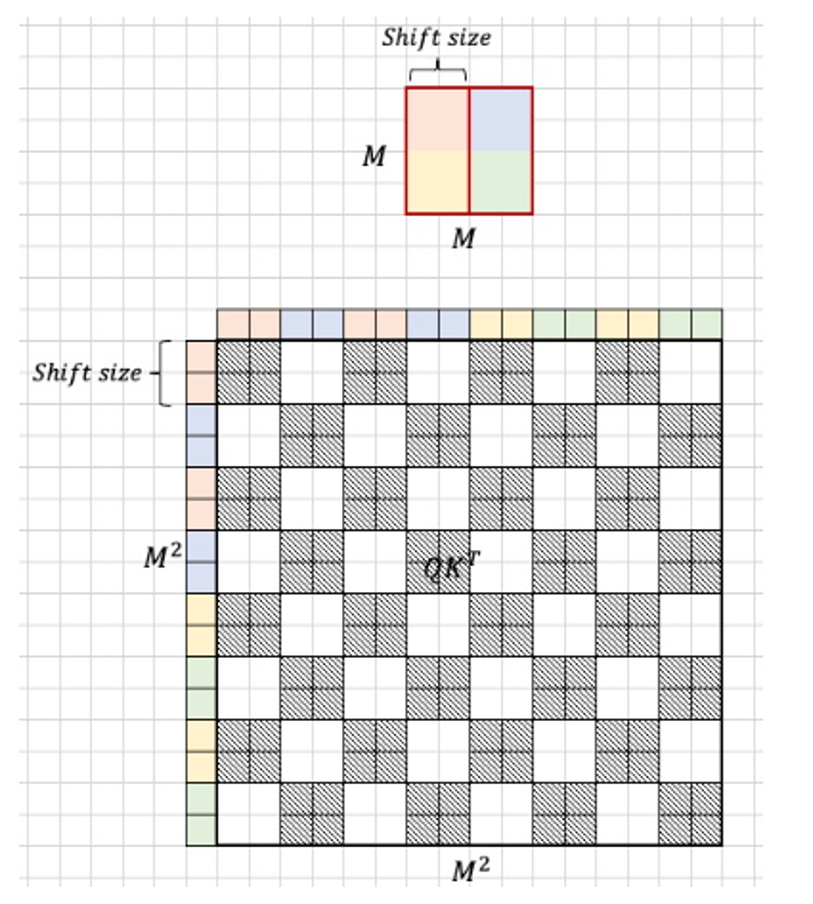
那么，对于剩下的两个组合后的窗口，他们的掩码又是什么样的呢？

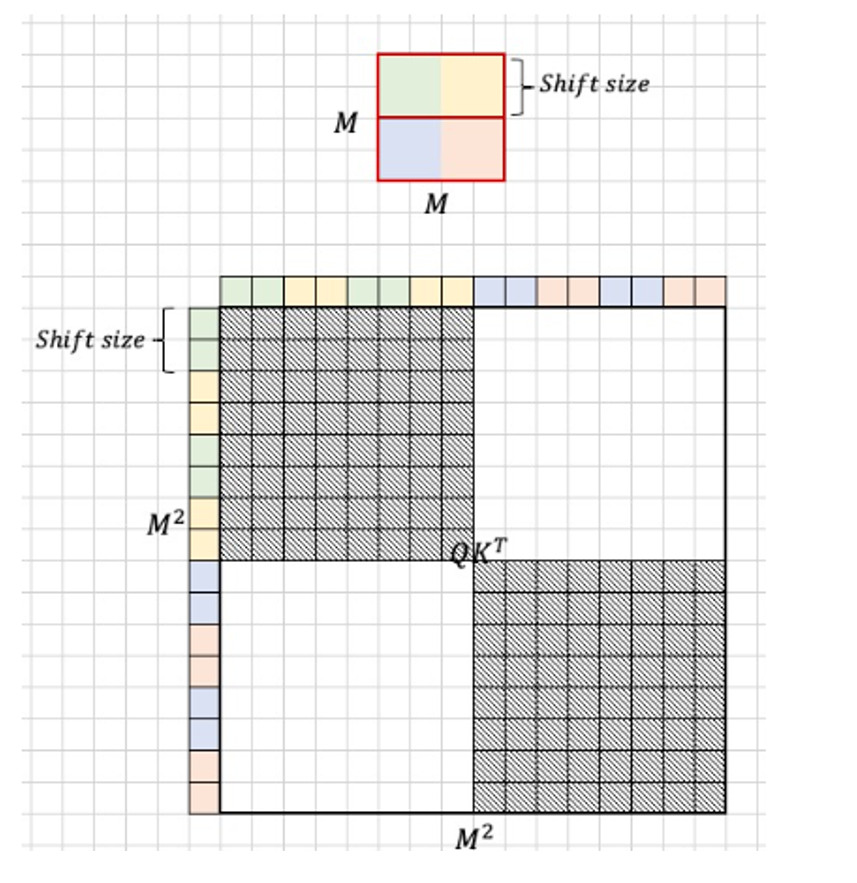
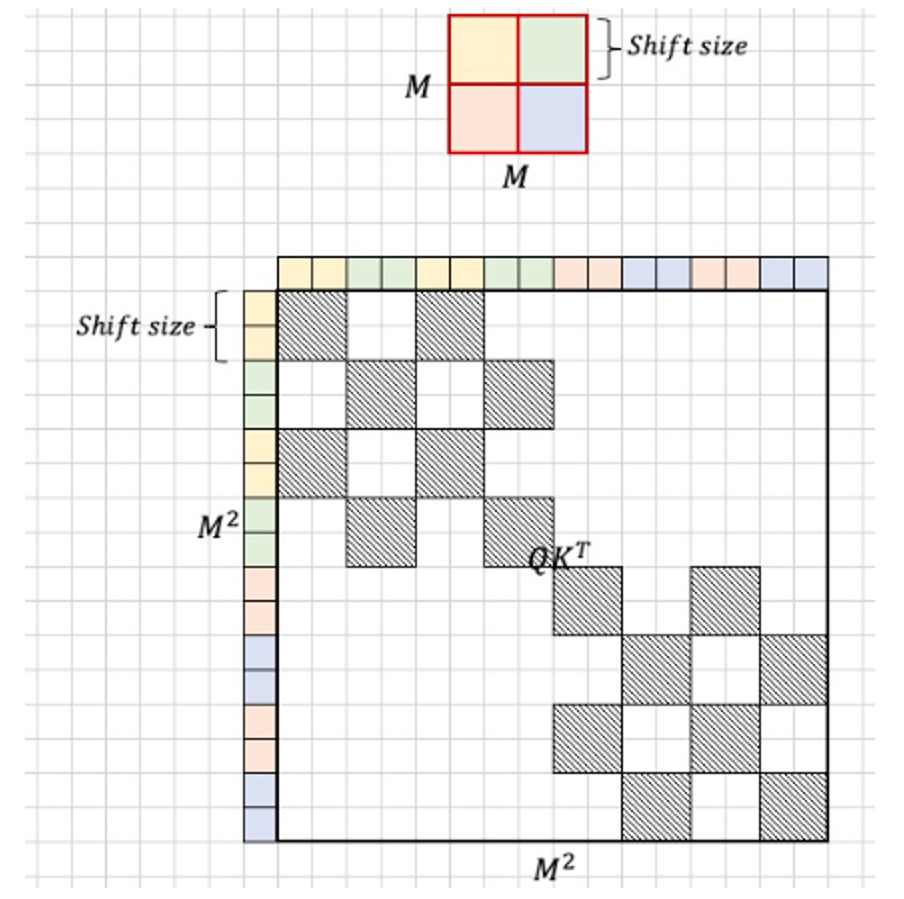
可以看到，不同组合窗口的类型，掩码是不同的。那么将这4个窗口的掩码汇总，他们对应的掩码如下

掩码的问题解决了。但是我们不能忽略一个问题。我们的swin-transformer-block是可以叠加的。这要求，被我们SW-MSA机制处理过后的图片的窗口，应该跟最开始输入W-MSA的窗口空间信息，应该是相同的。因此，我们在做好滑动窗口的attention计算后，还需要将窗口还原回去。

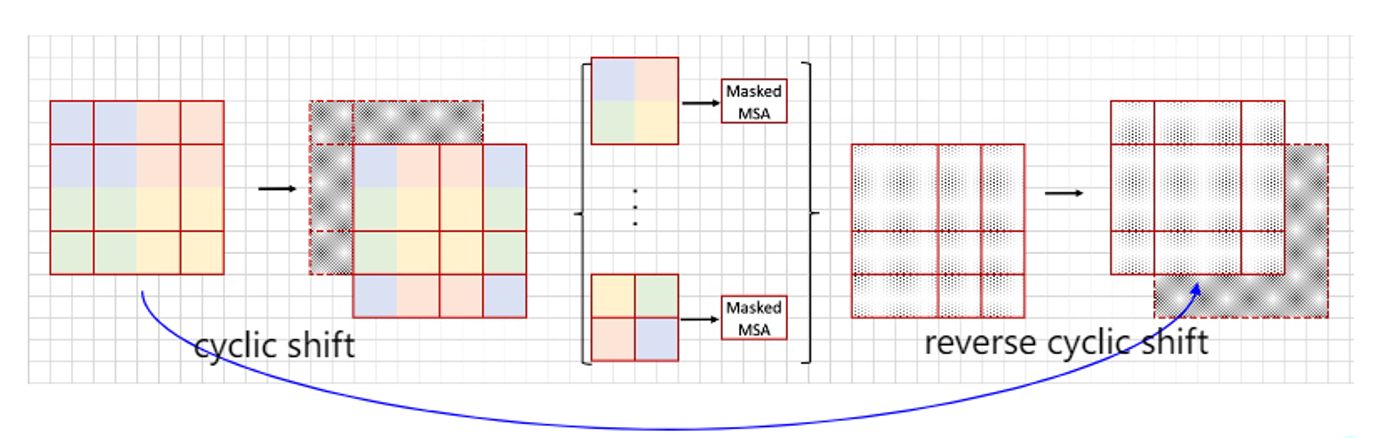
还原的方法如图所示，就是将滑动的窗口再方向滑动回去即可。这在代码中实现也不难。

上图为整个SW-MSA机制的操作流程。首先是滑动窗口，然后将部分窗口平移和组合，保持窗口数量和大小不变，最后对每个窗口加上掩码保证了最后计算的效果不变。计算完成后，要注意把窗口还原，方便下一次W-MSA计算的继续。

2.4Relative Position Bias

在论文中，作者在W-MSA和SW-MSA使用了相对位置偏执，能够给模型带来比较明显的提升。

使用这种位置编码的好处不言而喻，即对于每一个词向量x来说，无论相隔多远多近，互相影响程度是一样的，最粗暴的的情况当然是两个x 离的越远，互相之间的attention越小。因此我们需要给qk增加位置的编码的信息。而作者在实验结果中也说明，使用相对的位置编码比绝对位置编码效果更加好。下面我们来看相对位置偏移是如何实现的。

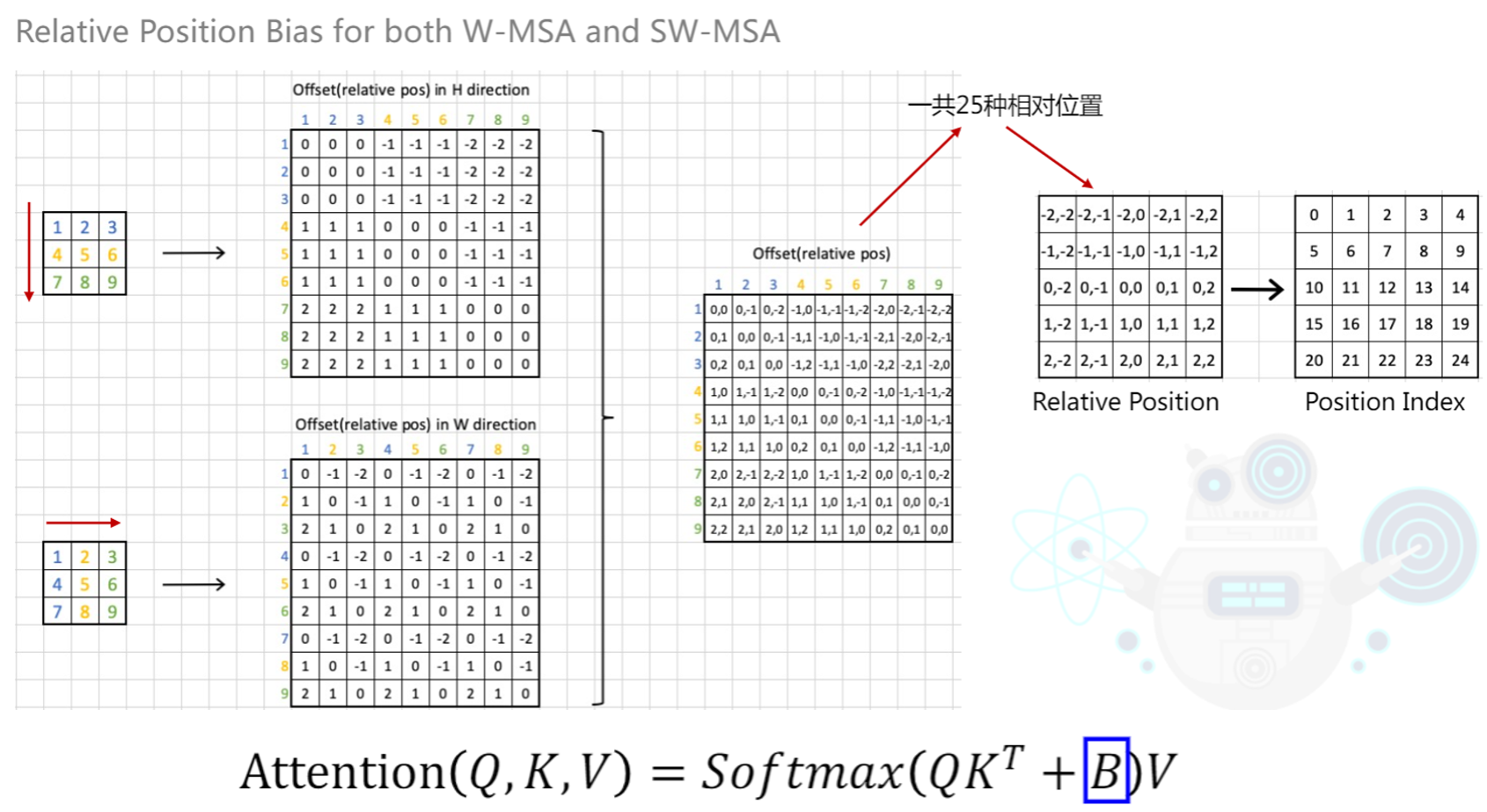
如图所示，对于一个词向量x，形状为 3 * 3.将它以高度方向（列方向）展开，其他颜色将获得一个相对与该颜色的相对偏移。第 i，j 列表示j相对与i的偏移量，比如，i=1 和 j=4按列展开，他们的偏移量是 4 相对 1的距离，为 1.并且我们这里标识，同颜色之间，偏移为0（可以理解为，一个词向量的每个维度的特征，他们之间距离为0）.这样，如上面那张图，按列方向展开，我们得到只有在 行方向 上的相对偏移量；同理，按照行展开，我们也能得到在 列方向的偏移量。将行偏移和列偏移后的矩阵两者结合，则可以得到一个行列偏移的表。这个表格每一种偏移的情况都对应了一个索引，而这个索引指向了真正的偏移。我们这里把所有可能形成的索引抽取了出来形成了一张相对位置索引表。

可以看到，表中 偏移 由 -2 到 2 一共5种数字构成，因此一共有 25 种相对偏执情况。而这个情况看上去不够清晰（不太方便用数组表示），于是我们通过一定的变换将其转成一维索引的形式，每个索引都会指向我们后面有一张相对偏移的表格。从代码的实现中，这样的变换为（以 4 * 4的矩阵为例，窗口大小M=2）：

1.为了保证偏移从0开始，行列偏移均 + M-1

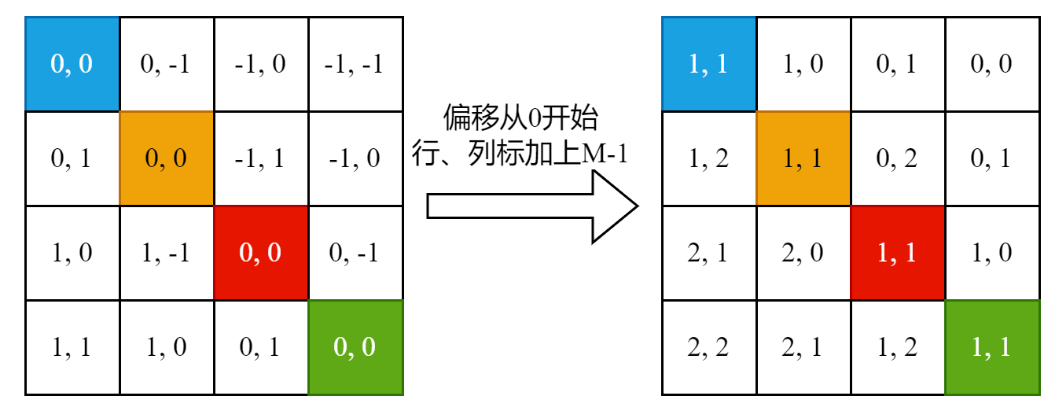
2.所有行标 乘上 2M -1,因为列偏移范围是从 0-2M-2的，行标 +2M-1相当于取值和列偏移错开。

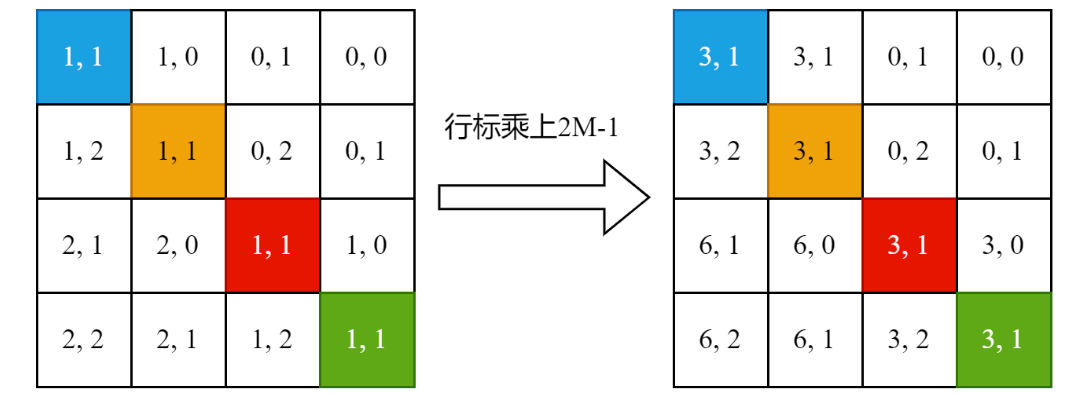
3.行列相加，形成一维索引

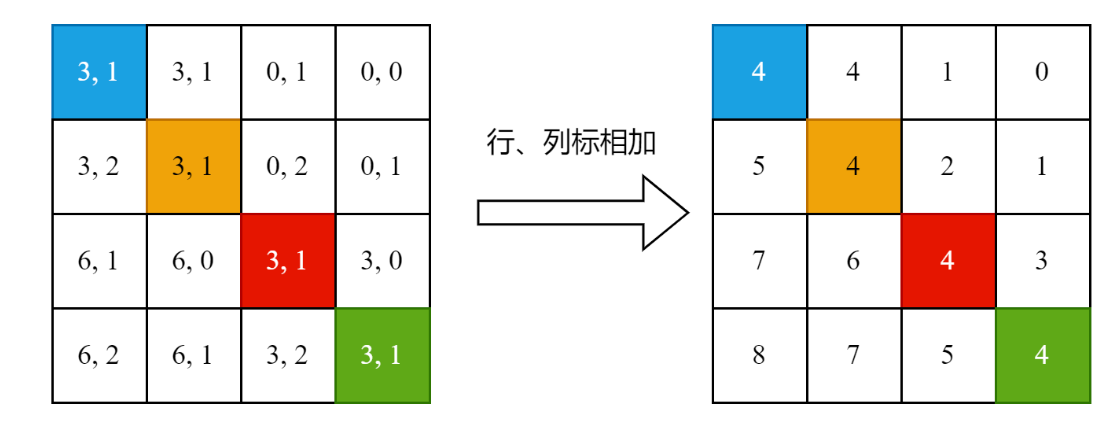
这样，变换过后的下标，是从 0 到（2M-1） * （2M -1 ）-1 的。

而这些索引需要对应相对偏移的Relative Position Bias Table B，这个B就是我们需要学习的参数了。(即下图蓝色框圈住的字母)

如何变换的过程说完了，那么我们返回原来的图。

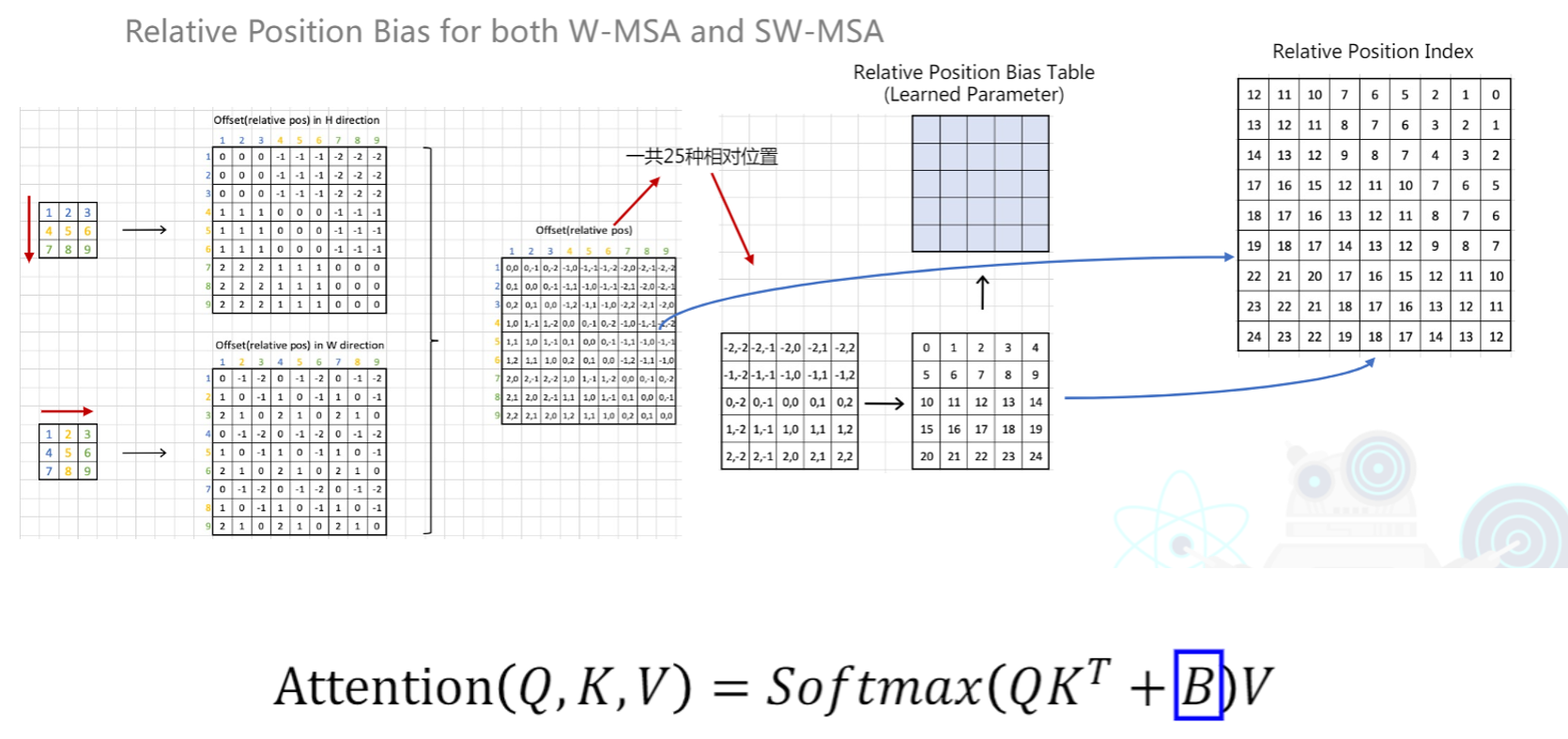
蓝色区域即为我们需要学习的相对位置偏移表，每个索引都将于上面的偏移表的值一一对应。这样，将相对位置偏移也纳入需要学习参数后，我们的相对位置偏移就说完了。

3.Patch Merging

为了提取更多尺度的信息，在论文中，使用了4个swin-transformer-block模块，而每一个模块对应了不同尺度的图像。而提取不同尺度，patch Merging 提供了这种下采样的操作。

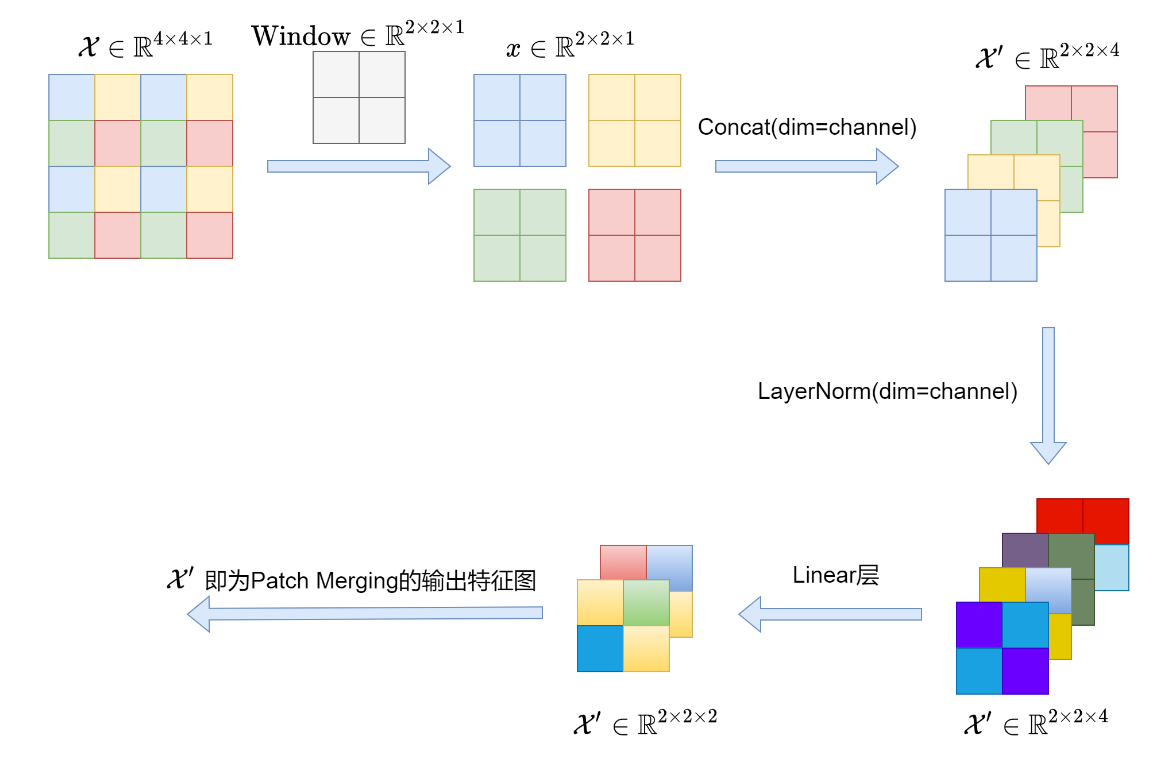
可以看到，patch merging 通过一次下采样的空洞卷积操作，将特征图的尺寸信息缩减为原来二分之一，通过特征维度上的concat，使得通道信息扩大为原来的4倍。再通过归一化layernorm和MLP的线性映射，最终将特征图从H * W * C下采样为

H/2 * W/2 * 2C。这样获得更大尺度的特征图，向下一级block传递，即可提取多尺度的特征。

四、总结

​ 在本文中，作者提出了一种计算机视觉领域的区别于传统卷积的骨干网络——Swin Transformer。该网络结构的关键创新在于W-MSA模块与SW-MSA模块，这两个模块相辅相成，使得网络不仅能够很好的关注细节信息并使计算量大幅减小，更同时保证了全局信息之间交流，使得该网络能够同时在图像分类、目标检测、语义分割等任务中取得很好的结果。