LDPC编译码基本原理
LDPC编译码基本原理
学习笔记 V1.1 2015/02/18 | LDPC编译码基本原理 |
概述 |
本文是个人针对LDPC的学习笔记,主要针对LDPC译码算法做了简要的总结。该版本主要致力于阐述LDPC码译码原理,这是一份有很多"问题"的总结,希望能够慢慢完善。本文分为以下几个部分 |

修订历史 | 以下表格展示了本文档的修订过程
|

本文提到的LDPC编码均指二进制LDPC编码,多进制暂时不进行讨论。为方便起见本文中混用了似然函数和条件概率密度这两个概念,虽然这样做是不恰当的。
LDPC码是一种校验矩阵具有低密度的线性分组码。也就是说,LDPC码和普通的线性分组码没有什么不同,但冠以"低密度"三字,说明以下两点问题
校验矩阵是一个相对通用的表示工具,线性分组码都可以由校验矩阵确定。通用性往往意味着很多时候难以表现一些特性,譬如,低密度。一个好的表示方式往往是解决问题的关键。图论中有一个图的矩阵表示,校验矩阵是稀疏的,一个好的表示就是指出其中1的位置,我们在意的也就是这些位置。如果将稀疏矩阵采用图来描述,这一个目的就达到了,这一类图被称为Tanner图,如图 1。 Tanner图和校验矩阵具有以下对应关系。Tanner图有
图 1 校验矩阵和Tanner图
此时我们可以先明确一些关于校验矩阵和Tanner图的定义
现在,我们应该好好考虑编译码的问题了。编码过程中,知道校验矩阵后生成矩阵是可以求出来的。求出生成矩阵后,至少可以说明编码是可进行的。利用其它的一些性质,这个过程可以变得更容易。(此部分内容还没有仔细看) 关于译码规则,香农在证明第二定理的时候采用了最大似然译码准则。当然,译码准则的选取还取决于信道。譬如,二进制对称信道下汉明距离译码和最大似然是一致的。然而,实际信道往往被看作是加性高斯白噪声信道,这个时候我们更多的需要考虑采用最大似然译码准则了。同时,毋庸置疑的是我们应该采用软判决译码以达到好的效果。此时,似然函数可以表示为 |

1962年Gallager提出了LDPC码的基本概率译码算法,本节将阐述这一思想。
解决一个大的问题的基本思路在于将其分解为一系列的小问题。对于似然函数而言,如果求 如果
发送信号通过信道后成为了接收信号
那么我们有
当我们致力于求解 注意到乘号左侧是和信道有关的,右边的 (1)当两个校验方程一样的时候
此时(一般情况下) (2)校验方程具有相同项
此时(一般情况下)
可以认为,如果校验方程行线性无关,那么
引理: 一个长为
证明:
将上述函数展开为关于
这个函数与前一个函数的区别在于:
同样可得,序列中"1"的个数为奇数的概率是
上文已经阐述 所以在基于除 这个前提是无法达到的,上述过程中我们也看到了求解每一个比特的概率通过校验方程环环相扣。或许,如果我们可以找到一个线头,这个问题可能就可以求解了。但很可惜的是,由于比特的相互依赖关系,计算概率的过程实际上是一个环。(大部分情况下是这样的)这个时候,概率译码直接将其修剪成了一棵树以计算概率分布。 修剪的原则在于,上层节点不能运用底层节点已经用过的校验信息,防止陷入循环。此时,通过绘制校验树,就能够求解后验概率分布。 概率译码给出了一种求解方式,那么这种针对单一比特的求解方式在真实的计算过程中是否可行?如果基于计算所有码元考虑是否有更好的计算方法?这种方法求得的解是否最优?在我看来,由于其余比特的概率是不准确的(不是最佳估计),此时我们也不能够得到求解比特的真实后验概率。 |

如果我们回到要求解的式子
在求解 或许另一种思路在于,对所有的 感性的认识是由于接收到了其他节点和校验方程的信息,迭代之后的估计会更好。另一个认识是如果Tanner图的某一个环的girth很短,那么自身的信息会大量的传递回来。因为距离越远,传递信息的比重就会越小(乘了太多小于1的数),环girth很长就不用考虑这个问题。但这还需要更多的理性分析。 下面具体阐述置信传播算法,假定编码后的星座映射为假定编码后的星座映射为 初始值 首先我们计算
图 2 信息传递过程
之后我们更新各个变量节点的概率分布
这个时候我们发现了一个问题,如果对于每一个校验节点来说,我们都给
××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××× 这一部分不是我写的,可以参考任意一本LDPC书,这里就不放上来了 这一部分不是我写的,可以参考任意一本LDPC书,这里就不放上来了×××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××
我们注意到在任何一种算法中,终止条件都有一条是校验式等于零。为何要设置这一个终止条件?实际上在设计的过程中,我们会保证任意两个可用码字之间的距离足够远。在这一个前提假设下,迭代过程中一旦落入了可用码字空间内,即使错误,那么也是几乎没有转移到正确码字的可能的。因此设置了这一终止条件。 |

从概率译码到置信传播,一个采用了校验集合树的概念,一个运用了Tanner图。然而我们实际上还是计算的公式,具体来说是
加法和乘法的运用构成了整个概率模型。但为何在这些算法中都引入了图?图在这里面起到了什么作用?《Pattern Recognition and Machine Learning》在图模型章节的开篇是这样说的
However, we shall find it highly advantageous to augment the analysis using diagrammatic representations of probability distributions, called probabilistic graphical models. These offer several useful properties: 1. They provide a simple way to visualize the structure of a probabilistic model and can be used to design and motivate new models. 2. Insights into the properties of the model, including conditional independence properties, can be obtained by inspection of the graph. 3. Complex computations, required to perform inference and learning in sophisticated models, can be expressed in terms of graphical manipulations, in which underlying mathematical expressions are carried along implicitly.
很多时候我们更关注问题的表示而非其本身。就像LDPC关注校验矩阵的形式,以及数据的各种变换。概率模型也一样,三种图模型被用来表示概率模型,包括有向图模型、无向图模型(马尔可夫随机场)和因子图。三种模型各有优点,本节将介绍因子图。 对于多项式而言,我们有因式分解。譬如在解高次方程的时候,我们非常希望方程能够分解为多个低次方程的乘积。那么,对于概率分布函数而言,我们也希望能够这样做,即 其中 那么这一个式子的因子图表示如下
图 3 因子图
从这个例子,我们总结一下因子图是什么?因子图有两类节点,一是变量节点,另一个成为因子节点。这两类节点的内部没有边直接相连,变量的概率密度可以因式分解为因子节点的函数的乘积,因子节点的函数变量包括与其直接相连的变量节点。 写到这里忽然发现了一个很严重的问题,因子图这一表示是用来干什么的?不是我不想写,是我也不知道。如果从和积算法来说,因子图可以用来计算边缘概率分布。这也是《Pattern Recognition and Machine Learning》中引入因子图的理由。置信传播算法可以看作是和积算法的一个特例。 目的:计算边缘概率 手段:和积算法(要求两个节点之间只有一条路径,即多项式树结构) 实现方式:
图 4 因子图的分解
这里为何要这样做呢?一个算法要尽可能多的利用已知的结构和信息,和积算法的一个假设是图无环。同时我们发现,对于一个最简单的只有一个变量节点和因子节点的图来说(这时实际上没有意义了),我们已经达到我们要的结果。如果图无环的话,意味着只要我断开一条边,那么这个大的因子图就变成了两个小的因子图。 如果我们将节点
其中
我们设 我们可以将其看作是因子节点
或许,我们将"计算"改为"表示"更为合适。上文中一直提到"小因子图"显然是可以因子化的,也就是说可以表示为
那么 也就是说,实际上这个过程是小因子图的继续划分的过程,具体可以表示为下图
图 5 因子图的分解(续)
同理可设
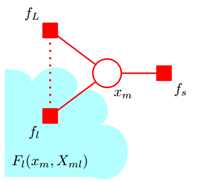
如果我们继续将其分解下去,那么将再次计算到因子节点向变量节点传递的信息,而我们的目的正是如此,希望能够得到
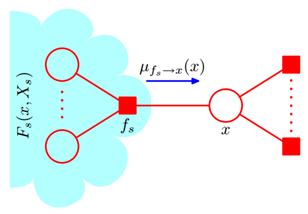
图 6因子图的分解(续2)
由图 6 易知 也就是说
和积和积,何为和积?变量节点的信息传递是求乘积的过程,因子节点传递的过程是对求乘积后的结果进行求和的过程(依据该因子节点的方程)。 我们注意到实际上都有一个连接的其他节点求乘积的过程,这也就意味着如果一个节点只和一个节点相连,那么其传递的消息是(和1相乘值不变)
到这里,因子图和和积算法已经写完了,要把因子图和和积算法和LDPC译码算法对应起来,我们要解决的问题实际上有两个
这两个问题还有待进一步思考…… |

参考 |
《LDPC码基础与应用》 贺鹤云 《An Introduction to Low-Density Parity Check Codes》 Daniel J. Costello, Jr. 《LDPC码理论与应用》 袁东风 《Pattern Recognition and Machine Learning》 |




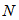 变量节点和
变量节点和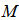 个校验节点,对应校验矩阵
个校验节点,对应校验矩阵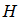 的列数和行数。如果第
的列数和行数。如果第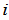 个变量节点和第
个变量节点和第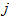 个校验节点之间有边相连,那么
个校验节点之间有边相连,那么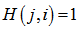 ,否则
,否则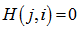 。显然,变量节点内部是没有边相连的,校验节点也是如此。
。显然,变量节点内部是没有边相连的,校验节点也是如此。
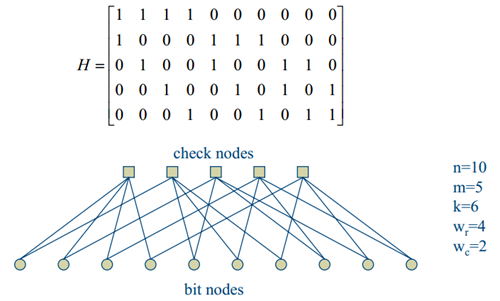
 ,其中
,其中 是接收序列,
是接收序列,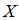 是编码后序列,
是编码后序列,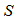 指
指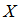 在码本空间内,即满足校验方程。显然,似然函数的计算是难以进行的。但早期Gallager作了很多工作。
在码本空间内,即满足校验方程。显然,似然函数的计算是难以进行的。但早期Gallager作了很多工作。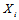 的概率密度可以达到同样的效果,即求
的概率密度可以达到同样的效果,即求 那么求解会方便很多。如果
那么求解会方便很多。如果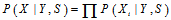 ,那么求解
,那么求解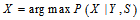 和求解
和求解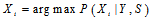 具有相同的效果。那么问题在于是否可以这样做。
具有相同的效果。那么问题在于是否可以这样做。
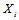 之间相互独立,这一关系显然是成立的;然而独立也就意味着不相关,那么这是不符合冗余度要求的。注意到我们求的是条件独立,条件是
之间相互独立,这一关系显然是成立的;然而独立也就意味着不相关,那么这是不符合冗余度要求的。注意到我们求的是条件独立,条件是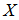 属于码本空间。
属于码本空间。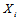 之间相互独立。
之间相互独立。
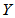 ,信道是加性高斯白噪声信道(从矢量信道模型去考虑)意味着
,信道是加性高斯白噪声信道(从矢量信道模型去考虑)意味着
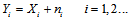
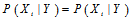 ,这是因为同样在码本空间内,
,这是因为同样在码本空间内, 的概率分布和
的概率分布和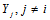 无关。
无关。
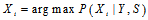 的时候,实际上我们只需要在0,1之间选择一个取值,所以我们可以分别计算0,1的概率,计算比值
的时候,实际上我们只需要在0,1之间选择一个取值,所以我们可以分别计算0,1的概率,计算比值
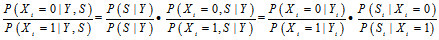
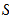 被
被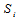 (包含
(包含 的方程)代替的原因是其他校验方程和条件是无关的。写到这里的时候,我们似乎计算不下去了。不妨做一个不切实际的假设,那就是除
的方程)代替的原因是其他校验方程和条件是无关的。写到这里的时候,我们似乎计算不下去了。不妨做一个不切实际的假设,那就是除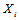 以外的其他概率分布已经求得了。当我们考虑一个校验方程的时候会发现
以外的其他概率分布已经求得了。当我们考虑一个校验方程的时候会发现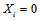 时该校验方程成立的条件是方程中其他的变量具有偶数个1,
时该校验方程成立的条件是方程中其他的变量具有偶数个1,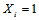 时正好相反。但是
时正好相反。但是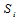 是多个校验方程的集合,如果说这些校验方程条件独立,将每一方程成立的概率相乘即可。那么问题是,什么时候校验方程条件独立?在回答这个问题之前,我们可以举出几个例子。
是多个校验方程的集合,如果说这些校验方程条件独立,将每一方程成立的概率相乘即可。那么问题是,什么时候校验方程条件独立?在回答这个问题之前,我们可以举出几个例子。

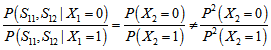
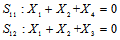
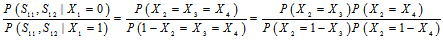
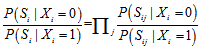
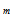 的相互独立的二进制序列,其中第
的相互独立的二进制序列,其中第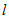 个比特为1的概率为
个比特为1的概率为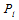 ,那么整个序列中包含偶数个1的概率是
,那么整个序列中包含偶数个1的概率是
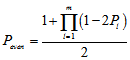
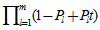
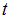 的多项式,则
的多项式,则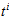 的系数表示这个长为m的序列中"1"的个数为
的系数表示这个长为m的序列中"1"的个数为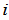 的概率。
的概率。
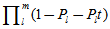
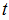 的奇数次幂的系数符号不同,两者正好互为正负。将这两个函数相加,那么
的奇数次幂的系数符号不同,两者正好互为正负。将这两个函数相加,那么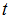 的偶次幂的系数为原函数的2倍,奇次项相加后消去。令
的偶次幂的系数为原函数的2倍,奇次项相加后消去。令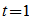 ,就可以得到序列中"1"的个数为偶数的概率:
,就可以得到序列中"1"的个数为偶数的概率:
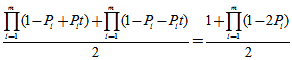
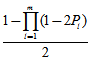
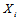 之间的条件独立特性,同时
之间的条件独立特性,同时
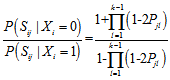
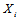 以外的其他概率分布已经求得
以外的其他概率分布已经求得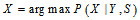 是可行的。4
是可行的。4
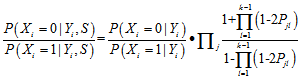
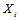 的过程中我们希望得到
的过程中我们希望得到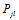 (第
(第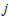 个方程的第
个方程的第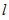 个节点为1的后验概率
个节点为1的后验概率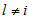 )的好的估计值。采用
)的好的估计值。采用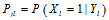 是一个很简单的选择,但是很显然不好,因为没有用到校验矩阵的约束信息。概率译码下考虑到了这一点,所以采用了树结构将校验矩阵的约束信息包含在其中。但是即使概率译码这样考虑了,实际上最顶层的节点采用的还是
是一个很简单的选择,但是很显然不好,因为没有用到校验矩阵的约束信息。概率译码下考虑到了这一点,所以采用了树结构将校验矩阵的约束信息包含在其中。但是即使概率译码这样考虑了,实际上最顶层的节点采用的还是 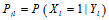 。
。
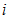 都采用
都采用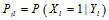 进行估计得到了一个更加好的估计,再用这些更好的估计进行迭代估计(所有节点并行估计)。
进行估计得到了一个更加好的估计,再用这些更好的估计进行迭代估计(所有节点并行估计)。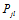 的更好的估计?
的更好的估计?
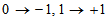
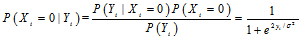
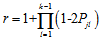
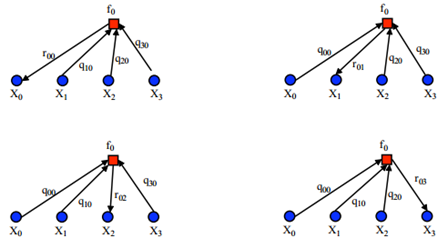

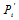 这一信息,那么刚从校验节点传递过来的信息立刻就被返回去了。所以
这一信息,那么刚从校验节点传递过来的信息立刻就被返回去了。所以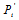 显然不是
显然不是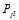 的更好的估计值。参考概率译码,我们至少能够做的是将其他节点传递的消息传递出去。(关于这个问题,不从得到
的更好的估计值。参考概率译码,我们至少能够做的是将其他节点传递的消息传递出去。(关于这个问题,不从得到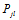 更好估计的角度,从消息传递的角度会更好解释,这将在因子图中介绍)因此置信传播的迭代过程应该是这样的。(参考《An Introduction to Low-Density Parity Check Codes》,本部分以下内容来自XXX师兄)
更好估计的角度,从消息传递的角度会更好解释,这将在因子图中介绍)因此置信传播的迭代过程应该是这样的。(参考《An Introduction to Low-Density Parity Check Codes》,本部分以下内容来自XXX师兄)


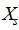 是
是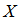 中变量的子集,至于到底能够如何分解是取决于问题的,就好象多项式的分解取决于其具体形式。对于一个实际的问题,如果有以下关系
中变量的子集,至于到底能够如何分解是取决于问题的,就好象多项式的分解取决于其具体形式。对于一个实际的问题,如果有以下关系
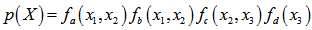

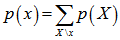
 表示除
表示除 之外的变量集合。
之外的变量集合。

 取出,那么因子图变成了
取出,那么因子图变成了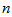 个小因子图,这几个小因子图通过节点
个小因子图,这几个小因子图通过节点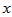 相连,故因子图的概率分布可以写成
相连,故因子图的概率分布可以写成
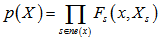
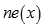 代表和
代表和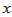 相连的因子节点,
相连的因子节点, 代表在这一个小因子图上的所有因子节点的乘积。
代表在这一个小因子图上的所有因子节点的乘积。
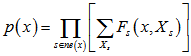
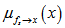 如下
如下
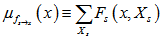
 传递的信息(也就是小因子图传递的)。
传递的信息(也就是小因子图传递的)。
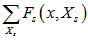

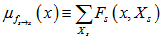 可以表示为
可以表示为
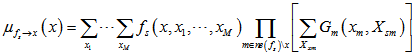
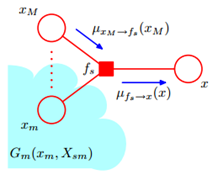
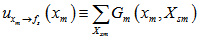 ,可将其看作变量节点向因子节点传递的信息。
,可将其看作变量节点向因子节点传递的信息。
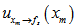 ,
,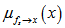 之间相对简单的公式,这样我们就能够计算出边缘概率分布了。
之间相对简单的公式,这样我们就能够计算出边缘概率分布了。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号