ACM模板【更新中】
\(Author: zhl\)
\(LastUpdate: 2020-10-14\)
0.其他
// ..,,***///////*,..
// ./#((((((((((((((((((((((//,.
// ,/((%&###(((((((((((((((((((((((((/,.
// .*((##&&%%%&&%%#(((((((((((((((((((((((##,
// ....,,,,,,**(##((((((((##%&%%#((((((((((((((((((%&((,.
// ..,,,,,,,,,,,,,,,*/(((((((((((#%%&%%%%%&&&&&&&&&&&&%/((*.
// .,,,,,,,,,,,,,,,,,,,,,*/(((((((((((%&%(((((((((((((#&&#((((.
// .,,*#%&%(,,,,*(%&%/,,,,,,/((((((((((%&%(((((((((((((((%&%((((,.,....
// .,,*#&&%(*,,,*#%&&#,,,,,,,*(((((((((%&%((((((((((((((((#&%#((#/,,,,.
// .,,,,**,*,,,,,,**,,,,,,,,,,/##((((((%&#(((((((((((((((((#&%%&%(,,.
// .,,,,,,(%#(##%%/,,,,,,,,,,,,(%%%#(((%&#(((((((((((((((##%&&%#((*.
// .,,,,,,,,****,,,,,,,,,,,,,,,*/(%&%#(%&#((((((((((#%&&&%%#(((((/,
// ,,,,,,,,,,,,,,,,,,,,,,,,,,*/(((#%%&&&&&&&&%%%%##(((((((((/*,.
// ..,,,,,,,,,,,,,,,,,,,,,,,,*(((((((((((((((((((((((/**,,,,,,.
// .,,,,,,,,,,,,,,,,,,,,,,*/((((((((((/(//***,,..,,,,,,,,,,,.
// .,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,..... .,,,,,,,,,,.
// .,,,,,,,,,,.. .,,,,,,,,,,,. ...........
// .,,,,,,,,,,. .,,,,,,,,,,,,
// ....... ..,,,,,,,,,,,.
龟龟
// #@@# . .,,,.
// /@@@@@& @@@@@&
// /@@@@ @@@@
// /% *(#%,,,,&%, .@@.
// ( ./* ,*. %
// ( * , .
// @@ ,. ., @@ @@@@,
// &@@@@. ., ,. . /@@@@@&&&&@@@@@.
// @@@@@@@@@@@@#* .,%@@@@@@@@@@@@@@@@@
// @@@@@@@, @@@@@@@@@@@@@@@@@@@@@@@@@@@@@@
// . @@@@@@ @@@@@@@@@@@@@@@@@@@@@@@@@@%%%&%&&@&%@&
// . .//, &@@@@ @@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@#%%&&
// (/,,, * @@@@@@@@@@@@@@@@@@@@@@@@@@@@@@&%%%@@/
// ((*//,,* #/&# @@@@@@@@@@@@@@@@@@@@@@@@@@@@@@#%%@@&@@@@@*
// #((###%%%%%#( .&@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@%&&@@%/@@@@@@
// %####%%%%%%%%%%,* @@@@@@@@@# @@@@@@@@@&&&@@
// ####%%%%%%%%%%/ @@@@@@@, @@@@@@@@@@&&@&
// (##((#%%%%%%%%# &@@. @@&...&%@@@@@&&
// /(((##%%%%%%%% @%,
// /((##%%%%%%%%
// ,#%&%#
快读
template<typename T>
void read(T& x)//输入
{
x = 0;
int f = 1;
char ch;
if ((ch = getchar()) == '-') f = -f;
else x = x * 10 + ch - '0';
while ((ch = getchar()) >= '0' && ch <= '9')
x = x * 10 + ch - '0';
x *= f;
}
template<typename T>
void print(T x) {
if (x < 0) {
putchar('-');
x = -x;
}
if (x > 9)
print(x / 10);
putchar(x % 10 + '0');
}
__int128可以直接使用
1.数学
gcd
辗转相除法
\(gcd(a,b) = gcd(b,a \% b)\)
int gcd(int a,int b){
return (a % b == 0) ? b : gcd(b, a % b);
}
//或者直接用__gcd()
快速幂
int qpow(int a, int p) {
int ans = 1;
while (p) {
if (p & 1) ans = ans * a % mod;
a = a * a % mod;
p >>= 1;
}
return ans;
}
逆元
费马小定理
\(inv(a) = a^{mod-2}\)
递推打表
\[p = k * i + r
\\k*i + r = 0 (mod\ p)\\
k*inv[r] + inv[i] = 0\\
inv[i] = -\dfrac pi *inv[r]
\]
$ inv[i] = (mod\ -\ mod/i)*inv\ [mod%i\ ]%mod $
void get_inv(){
inv[1] = 1;
for(int i = 2;i < maxn;i++){
inv[i] = (mod - mod / i) * inv[mod % i] % mod;
}
}
欧拉筛（线筛）
void get_phi(int n) {
for (int i = 2; i <= n; i++) {
if (!book[i]) {
prime[++cnt] = i;
phi[i] = i - 1; // i是素数
}
for (int j = 1; j <= cnt; j++) {
if (i * prime[j] > n) break;
book[i * prime[j]] = 1;
phi[i * prime[j]] = phi[i] * phi[prime[j]];
if (!i % prime[j]) {
phi[i * prime[j]] = phi[i] * prime[j];
break;
}
}
}
}
整除分块
for(int l = 1,r = 0;l <= n;l = r + 1){
r = n/(n/l);
//sum += (n/l)*(r-l+1);
}
扩展欧几里得
首先看看二元一次不定方程
ax + by = c
①若gcd(a,b) | c，则方程有整数解
此时，方程左右同时处以gcd(a,b)
则此时a,b互素
此时只需要解方程
ax + by = 1即可，因为将解翻倍即可得到右边不为1的其他解，（a,b此时互素)
扩展欧几里得，将方程 ax + by == gcd(a,b) 求解，并顺便解除gcd(a,b)
void ex_gcd(int a,int b,int &gcd,int &x,int &y){
if(b == 0){
x = 1;
y = 0;
gcd = a;
}
else{
ex_gcd(b,a % b,gcd,y,x); //a,b交换，x,y跟着交换，大概应该是这个意思
y -= x*(a/b);
}
}
ex_gcd还可以求逆元；
**ex_gcd(a,m,x,y), 则 x = inv(a) (mod m) **
此时m可以不为素数。
中国剩余定理
问题
$x\equiv a_1 ( mod\ m_1) $
\(x \equiv a_2(mod\ m_2)\)
\(......\)
\(x \equiv a_k(mod\ m_k)\)
其中 \(m\) 两两互素
int CRT(){
int res = 0,M = 1;
int x,y,gcd;
for(int i = 1;i <= k;i++){
M *= m[i];
}
for(int i = 1;i <= k;i++){
int tmp = M / m[i];
ex_gcd(tp,m[i],gcd,x,y);
x = (x % m[i] + m[i]) % m[i];
res = (res + tmp * a[i] * x) % M;
}
return (res + M) % M;
}
扩展中国剩余定理
取消了两两互素的限制
int EX_CRT(){
int x,y,k,gcd;
int M = m[1];int res = a[1];
for(int i = 2;i <= k;i++){
int a = M,b = m[i], c = ((a[i] - res) % b + b) % b;
ex_gcd(a,b,gcd,x,y);
int tmp = b / gcd;
if(c % gcd != 0) return -1; //方程无解
x = mul(x,c/gcd,tmp); //因为系数不为1
res += x*M;
M *= tmp;
res = (res % M + M) % M;
}
return (res % M + M) % M;
}
欧拉降幂
\[a^b(mod\ n) = \begin{cases}
a^{b\ \% \ \varphi(n)} &(mod\ n),&&a和n互质\\
a^b \ & \ (mod \ n),&&b<\varphi(n)\\
a^{b\ \% \ \varphi(n)+\varphi(n)}&(mod\ n),&&b\ge\varphi(n)
\end{cases}
\]
求欧拉函数
欧拉筛
直接计算
int euler_phi(int n) {
int m = (int)sqrt(n + 0.5);
int ans = n;
for (int i = 2; i <= m; ++i) {
if (n % i == 0) {
ans = ans / i *(i - 1);
while (n % i == 0) n /= i;
}
}
if (n > 1) ans = ans / n *(n - 1);
return ans;
}
杜教筛
要求的东西 ： \(\sum f(i)\)
设
\[h = f * g
\]
记 \(S(n) = \sum_{i=1}^{n}f(i)\)
\[\sum_{i=1}^{n}h(i)=\sum_{i=1}^{n}\sum_{d|i}g(d)\cdot f(\frac{i}{d})\\\to =\sum_{d=1}^{n}g(d)\cdot\sum_{i=1}^{\lfloor\frac{n}{d}\rfloor}f({i})
\]
\[\to \sum_{i=1}^{n}h(i)=\sum_{d=1}^{n}g(d)\cdot S(\lfloor\frac{n}{d}\rfloor)
\]
这一步的两个 \(\sum\) 的位置变换可以自己在纸上举了例子体会一下
\[\sum_{i=1}^{n}h(i)=g(1)\cdot S(n)+\sum_{d=2}^{n}g(d)\cdot S(\lfloor\frac{n}{d}\rfloor)
\]
\[\to g(1)S(n)=\sum_{i=1}^{n}h(i)-\sum_{d=2}^{n}g(d)\cdot S(\lfloor\frac{n}{d}\rfloor)
\]
#include<bits/stdc++.h>
#include<unordered_map>
using namespace std;
template<typename T>void read(T& x) {
x = 0;
int p = 1;
char c = getchar();
while (!isdigit(c)) { if (c == '-')p = -1, c = getchar(); }
while (isdigit(c)) { x = (x << 1) + (x << 3) + (c - 48); c = getchar(); }
x *= p;
}
template<typename T>void write(T x) {
if (x < 0) putchar('-'), x = -x;
if (x > 9) write(x / 10);
putchar(x % 10 + '0');
}
typedef long long ll;
const int maxn = 6e6 + 10;
int mu[maxn];
ll phi[maxn];
int sum_mu[maxn];
ll sum_phi[maxn];
int vis[maxn];
int prime[maxn], cnt;
unordered_map<int, ll>MU, PHI;
void get(int N) {
phi[1] = mu[1] = 1;
for (int i = 2; i <= N; i++) {
if (!vis[i]) {
prime[++cnt] = i;
mu[i] = -1;
phi[i] = i - 1;
}
for (int j = 1; j <= cnt && prime[j] * i <= N; j++) {
vis[prime[j] * i] = 1;
if (i % prime[j] == 0) {
phi[i * prime[j]] = phi[i] * prime[j];
break;
}
else {
mu[i * prime[j]] = mu[i] * -1;
phi[i * prime[j]] = phi[i] * (prime[j] - 1);
}
}
}
for (int i = 1; i <= N; i++) {
sum_phi[i] = sum_phi[i - 1] + phi[i];
sum_mu[i] = sum_mu[i - 1] + mu[i];
}
}
ll djs_mu(ll x) {
if (x <= maxn - 10)return sum_mu[x];
if (MU.count(x) != 0)return MU[x];
int ans = 1;
for (int l = 2, r;l <= x; l = r + 1) {
r = x / (x / l);
ans -= (r - l + 1) * djs_mu(x / l);
}
return MU[x] = ans;
}
ll djs_phi(ll x) {
if (x <= maxn - 10)return sum_phi[x];
if (PHI.count(x) != 0)return PHI[x];
ll ans = x * (x + 1) / 2;
for (ll l = 2, r; l <= x; l = r + 1) {
r = x / (x / l);
ans -= (r - l + 1) * djs_phi(x / l);
}
return PHI[x] = ans;
}
int main() {
int t, n;
read(t);
get(maxn - 10);
while (t--) {
read(n);
write(djs_phi(n)); putchar(' ');
write(djs_mu(n)); puts("");
}
}
min25筛
一种低于线性复杂度的求积性函数前缀和的筛法。
适用条件：
- \(f(p)\) 是多项式
- \(f(p^k)\) 便于计算
思想：
\[\sum_{i=1}^nf(i) = \sum_{i \in Prime}f(i) + \sum_{i \notin Prime}f(i)
\]
分为两个部分，第一部分是所有素数，第二部分是所有的合数
第一部分
搞来一个这样的函数 \(g(n,j)\)
\[g(n,j) = \sum_{i=1}^n[i \in Prime\ or\ minp(i) > P_j] i^k
\]
所有的素数加上满足\(minp(i) > P_j\) 的所有 \(i\)
\([1-n]\) 中所有质数的 \(k\) 次方之和就是 \(g(n,x)\) ，\(P_x\) 是最后一个小于等于
\(\sqrt n\) 的质数
考虑 \(g(n,j)\) 的转移
\[g(n,j) = g(n,j-1) - P_j^k\bigg(g(\dfrac n {P_j},j-1)\ -g(P_j-1,j-1)\bigg)
\]
这个东西自己在纸上写一些体会一下，注意 \(P_j\) 筛去的第一个数是 \(P_j^2\) , 第二个数不是 \(P_j^2+ P_j\)
第二部分
设
\[S(n,x) = \sum_{i=1}^n[minp(i) > P_x]f(i)
\]
可以把 \(S(n,x)\) 也分成两部分，一部分是所有大于 \(P_x\) 的质数，另一部分是最小质因数大于 \(P_x\) 的合数，枚举最小质因子
\[S(n,x) = g(n) - sp_x + \sum_{p_k^e \le n \&k>n}f(p_k^e)\bigg(S \bigg(\dfrac n {p_k^e}\bigg) + [e \ne 1]\bigg)
\]
当 \(e = 1\) 的时候， \(P_k\) 在前面枚举过了，不等于 \(1\) 时，需要加上 \(P_k^e\)
存下所有可能的 \(\lfloor\dfrac n x \rfloor\) , 做一个映射
\[idx(x)= \begin{cases}
ind1[x] , \ \ x\le \sqrt n \\
ind2[n/x],\ \ x>\sqrt n
\end{cases}
\]
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll mod = 1e9 + 7, inv6 = 166666668, inv2 = 500000004;
const int maxn = 1e6 + 10;
ll n, sqr;
ll prime[maxn], cnt, vis[maxn];
ll sp1[maxn], sp2[maxn];//sp1 p的前缀和，sp2 p^2的前缀和
ll w[maxn], tot;
ll g1[maxn], g2[maxn], ind1[maxn], ind2[maxn];
void get(int maxn) {
for (int i = 2; i <= maxn; i++) {
if (!vis[i]) {
prime[++cnt] = i;
sp1[cnt] = (sp1[cnt - 1] + i) % mod;
sp2[cnt] = (sp2[cnt - 1] + 1ll * i * i) % mod;
}
for (int j = 1; j <= cnt && prime[j] * i <= maxn; j++) {
vis[prime[j] * i] = 1;
if (i % prime[j] == 0)break;
}
}
}
ll S(ll x, int y){
if (prime[y] >= x)return 0;
ll k = x <= sqr ? ind1[x] : ind2[n / x];
ll ans = (g2[k] - g1[k] + mod - (sp2[y] - sp1[y]) + mod) % mod;
for (int i = y + 1; i <= cnt && prime[i] * prime[i] <= x; i++)
{
ll pe = prime[i];
for (int e = 1; pe <= x; e++, pe = pe * prime[i])
{
ll xx = pe % mod;
ans = (ans + xx * (xx - 1) % mod * (S(x / pe, i) + (e != 1))) % mod;
}
}
return ans % mod;
}
int main() {
scanf("%lld", &n);
sqr = sqrt(n);
get(sqr);
for (ll l = 1, r; l <= n; l = r + 1) {
r = n / (n / l);
w[++tot] = n / l;
ll k = w[tot] % mod;
g1[tot] = (k * (k + 1) % mod * inv2 - 1 + mod) % mod;
g2[tot] = (k * (k + 1) % mod * (2 * k + 1) %mod * inv6 % mod + mod - 1) % mod;
if (w[tot] <= sqr)ind1[n / l] = tot;
else ind2[n / (n / l)] = tot;
}
for (int i = 1; i <= cnt; i++) {
//g(n,j) 滚第一维
for (int j = 1; j <= tot && prime[i] * prime[i] <= w[j]; j++) {
ll k = w[j] / prime[i] <= sqr ? ind1[w[j] / prime[i]] : ind2[n / (w[j] / prime[i])];
g1[j] -= prime[i] * (g1[k] - sp1[i - 1] + mod) % mod;
g2[j] -= prime[i] * prime[i] % mod * (g2[k] - sp2[i - 1] + mod) % mod;
g1[j] %= mod; g2[j] %= mod;
if (g1[j] < 0)g1[j] += mod;
if (g2[j] < 0)g2[j] += mod;
}
}
printf("%lld\n", (S(n, 0) + 1) % mod); //f(1) = 1
}
常见生成函数
有三种物品，分别有 3 ，2， 3个，问拿四个的方案数
f[i][j] 表示当前第 i 个位置，已经选了 j 个物品的方案数
f[0][0] = 1;
for(int i = 1;i <= 3;i++){
for(int j = 0;j <= 8;j++){//总共要选j个
for(int k = 0;k <= j;k++){//已经选了k个
if(j - k <= v[i])//此时要选j-k个
f[i][j] += f[i-1][k];
}
}
}
第一种物品的生成函数 \(G_1(x) = 1 + x + x^2 + x ^ 3\)
\(G_2(x) = 1 + x + x^2\) , $G_3 = 1 + x + x^2 + x^3 $
\(G_1(x)*G_2(x)*G_3(x)\) ,中 \(x^4\) 的系数就是答案
上述代码其实就是在求多项式乘法的系数
指数生成函数
将上述问题改成排列方案hdu1521
构造出
\(G_1(x) = 1+\frac{x^1}{1} + \frac{x^2}{2!} + \frac{x^3}{3!}\)
\(G_2(x) = 1 + \frac{x^1}{1} + \frac{x^2}{2}\)
\(G_3(x) = 1 + \frac{x^1}{1} + \frac{x^2}{2!} + \frac{x^3}{3!}\)
\[\begin{aligned}
G_e(x) &= (1 + \frac{x}{1!} + \frac{x^2}{2!} + \frac{x^3}{3!})(1+\frac{x}{1!} + \frac{x^2}{2!}) (1 + \frac{x}{1!} + \frac{x^2}{2!} + \frac{x^3}{3!})\\
&= (1+2x+2x^2+\frac{7}{6}x^3 + \frac{5}{12}x^4 + \frac{1}{12}x^5) (1+x+\frac{1}{2}x^2 + \frac{1}{6}x^3)\\
&=(1+3x + \frac{9}{2}x^2 + \frac{14}{3}x^3 + \frac{35}{12}x^4 + \frac{17}{12}x^5 + \frac{35}{72} x^6 + \frac{8}{72}x^7 + \frac{1}{71}x^8)
\end{aligned}
\]
答案就是 \(x^4\) 的系数乘上 \(4!\) ， \(\frac{35}{12} * 4! = 70\)
(1-x)^-1 型
\[\dfrac 1 {1-x} = \sum_{i=0}^\infty x^i
\]
广义二项式定理
\[\dfrac 1 {(1-x)^n} = \sum_{i=0}^{\infty} C_{n+i-1}^i x^i
\]
至多为 \(k\) 就是 \(\dfrac {1-x^{k+1}} {1-x}\)
\(k\) 的倍数就是 \(\dfrac 1 {1-x^k}\)
最后的结果是 \(\dfrac 1 {(1-x)^5}\) ， 带入广义二项式定理， 答案是 \(C_n^4\)
\(py\) 草不过去， \(OI\)👴直呼 人生苦短我用 \(ruby\)
e^x 型
\[e^x = \sum_{i=0}^\infty \dfrac {x^i} {i!}
\]
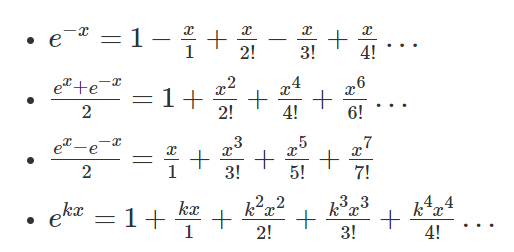
五边形数定理
整数拆分
五边形数定理
这里的欧拉函数 \(\phi(q)\) 是复变函数
\[\phi(q) = \prod_{k=1}^\infty (1-q^k)
\]
五边形数定理描述了欧拉函数的展开式特性
\[(1-x)(1-x^2)(1-x^3)... = 1 -x-x^2+x^5+x^7-x^{12}-x^{15}+x^{22}+x^{26}+...
\]
欧拉函数展开后，有些次方项被消去，只留下次方项为1, 2, 5, 7, 12, ...的项次，留下来的次方恰为广义五边形数。
拆分函数 \(p(n)\)
\[\sum_{n=0}^{\infty}p(n)x^n = \prod_{k=1}^{\infty}(\frac{1}{1-x^k})
\]
\[1取了多少次->(1+x^1+x^2+x^3+…) \\ 2取了多少次->(1+x^2+x^4+x^6+…) \\ 3取了多少次->(1+x^3+x^6+x^9+…) \\ \vdots \\ \sum_{n=0}^{\infty}p(n)x^n = (1+x^1+x^2+x^3+…)(1+x^2+x^4+x^6+…)(1+x^3+x^6+x^9+…) \cdots
\]
根据欧拉发现的五边形数定理，描述欧拉函\(ϕ(x)\)如下：
\[\prod_{n=1}^{\infty}(1-x^n) = \sum_{k=-\infty}^{\infty} (-1)^kx^{k(3k-1)/2} = \sum_{k=0}^{\infty} (-1)^kx^{k(3k \pm 1)/2} \\ (1-x)(1-x^2)(1-x^3) … = 1-x-x^2+x^5+x^7-x^{12}-x^{15}+x^{22}+x^{26}+… \\ 这些系数都属于广义五边形数
\]
那么我们就很容易发现欧拉函数的导数是分割函数的母函数：
\[\frac{1}{\phi(x)} = \sum_{k=0}^{\infty} p(k)x^k \quad <=> \quad 1 = \phi(x)\sum_{k=0}^{\infty} p(k)x^k \\ (1-x-x^2+x^5+x^7-x^{12}-x^{15}+x^{22}+x^{26}+…)(1+p(1)x+p(2)x^2+p(3)x^3+…) = 1
\]
那么在考虑\(x^n\)项的系数的时候，在\(n>0\)的情况下，系数都为0，那么就能得到
\[p(n)-p(n-1)-p(n-2)+p(n-5)+p(n-7)+… = 0 \\ p(n) = p(n-1)+p(n-2)-p(n-5)-p(n-7)+ …
\]
这个的时间复杂度可以在O(nlogn)时间内解决。
暂时不知道怎么 \(nlogn\) 搞，好像要多项式求逆啥的
待补
但是可以 \(O(n\sqrt n)\) 搞
#include <iostream>
using namespace std;
typedef long long ll;
const ll N = 500005, mod = 998244353;
ll f[N], g[N], dp[N];
int n;
int main() {
scanf("%d", &n);
--n;
for (ll i = 1; i <= n; ++i) f[i] = i * (3*i - 1) / 2;
for (ll i = 1; i <= n; ++i) g[i] = i * (3*i + 1) / 2;
dp[0] = 1;
for (int i = 1; i <= n; ++i) {
for (int j = 1; f[j] <= i; ++j) {
if (j & 1) {
dp[i] += dp[i - f[j]];
if (g[j] <= i) dp[i] += dp[i - g[j]];
} else {
dp[i] -= dp[i - f[j]];
if (g[j] <= i) dp[i] -= dp[i - g[j]];
}
}
dp[i] %= mod;
if (dp[i] < 0) dp[i] += mod;
}
printf("%lld\n", dp[n]);
return 0;
}
FFT
由 系数表示法 转换为 点值表示法
记
\[\omega_n^k = cos(\dfrac {2\pi\cdot k} n) + i \cdot sin(\dfrac {2\pi \cdot k} n)
\]
\[A(x)=a_0+a_1*x+a_2*{x^2}+a_3*{x^3}+a_4*{x^4}+a_5*{x^5}+\\ \dots+a_{n-2}*x^{n-2}+a_{n-1}*x^{n-1}
\]
\[A(x)=(a_0+a_2*{x^2}+a_4*{x^4}+\dots+a_{n-2}*x^{n-2})+\\(a_1*x+a_3*{x^3}+a_5*{x^5}+ \dots+a_{n-1}*x^{n-1})
\]
设
\[A_1(x)=a_0+a_2*{x}+a_4*{x^2}+\dots+a_{n-2}*x^{\frac{n}{2}-1}
\]
\[A_2(x)=a_1+a_3*{x}+a_5*{x^2}+ \dots+a_{n-1}*x^{\frac{n}{2}-1}
\]
则
\[A(x)=A_1(x^2)+xA_2(x^2)
\]
带入 \(x = \omega_n^k\)
\[A(\omega_n^k) = A_1(\omega_{\frac n2}^k) + \omega_n^kA_2(\omega_{\frac n2}^k)
\]
带入 $x = \omega_n^{k+\frac n2} $
\[A(\omega_n^{k+\frac n2}) = A_1(\omega_{\frac n2}^k) -\omega_n^kA_2(\omega_{\frac n2}^k)
\]
也就是说如果知道了 $A_1(x),A_2(x) $ 分别在 \(\omega_{\frac n2}^0\) , \(\omega_{\frac n2}^1\) , \(\omega_{\frac n2}^2\) ,...,\(\omega_{\frac n2}^{\frac n2 -1}\) 的取值，
就可以 \(O(n)\) 的求出 \(A(x)\)
void fft(cp *a,int n,int inv)//inv是取共轭复数的符号
{
if (n==1)return;
int mid=n/2;
static cp b[MAXN];
for(int i = 0;i < mid;i++)b[i]=a[i*2],b[i+mid]=a[i*2+1];
for(int i = 0;i < n;i++)a[i]=b[i];
fft(a,mid,inv),fft(a+mid,mid,inv);//分治
for(int i = 0;i < mid;i++)
{
cp x(cos(2*pi*i/n),inv*sin(2*pi*i/n));//inv取决是否取共轭复数
b[i]=a[i]+x*a[i+mid],b[i+mid]=a[i]-x*a[i+mid];
}
for(int i = 0;i < a;i++)a[i]=b[i];
}
每个位置分治后最终的位置是二进制翻转后的位置
void fft(cp *a,int n,int inv)
{
int bit=0;
while ((1<<bit)<n)bit++;
fo(i,0,n-1)
{
rev[i]=(rev[i>>1]>>1)|((i&1)<<(bit-1));
if (i<rev[i])swap(a[i],a[rev[i]]);//不加这条if会交换两次（就是没交换）
}
for (int mid=1;mid<n;mid*=2)//mid是准备合并序列的长度的二分之一
{
cp temp(cos(pi/mid),inv*sin(pi/mid));//单位根，pi的系数2已经约掉了
for (int i=0;i<n;i+=mid*2)//mid*2是准备合并序列的长度，i是合并到了哪一位
{
cp omega(1,0);
for (int j=0;j<mid;j++,omega*=temp)//只扫左半部分，得到右半部分的答案
{
cp x=a[i+j],y=omega*a[i+j+mid];
a[i+j]=x+y,a[i+j+mid]=x-y;//这个就是蝴蝶变换什么的
}
}
}
}
注意 lim
#include<bits/stdc++.h>
using namespace std;
const double pi = acos(-1.0);
const int N = 3e6 + 10;
struct cp {
double x, y;
cp() {}
cp(double _x, double _y) {
x = _x; y = _y;
}
cp operator + (cp b) {
return cp(x + b.x, y + b.y);
}
cp operator -(cp b) {
return cp(x - b.x, y - b.y);
}
cp operator *(cp b) {
return cp(x * b.x - y * b.y, x * b.y + y * b.x);
}
};
int rev[N];
int bit = 0;
int lim;
void FFT(cp* a, int inv) {
for (int i = 0; i < lim; i++) {
if (i < rev[i]) {
swap(a[i], a[rev[i]]);
}
}
for (int mid = 1; mid < lim; mid <<= 1) {
cp temp(cos(pi / mid), inv * sin(pi / mid));
for (int i = 0; i < lim; i += mid * 2) {
cp omega(1, 0);
for (int j = 0; j < mid; j++, omega = omega * temp) {
cp x = a[i + j], y = omega * a[i + j + mid];
a[i + j] = x + y, a[i + j + mid] = x - y;
}
}
}
}
int n, m;
cp A[N], B[N];
int main() {
scanf("%d%d", &n, &m);
lim = 1;
while (lim <= n + m)lim<<=1,bit++;//调整至 2^k
for (int i = 0; i < lim; i++) {
rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));
}
for (int i = 0; i <= n; i++)scanf("%lf", &A[i].x), A[i].y = 0;
for (int i = 0; i <= m; i++)scanf("%lf", &B[i].x), B[i].y = 0;
FFT(A, 1);
FFT(B, 1);
for (int i = 0; i <= lim; i++) {
A[i] = A[i] * B[i];
}
FFT(A, -1);
for (int i = 0; i <= n + m; i++) {
printf("%d ", int(A[i].x /lim+0.5));
}
}
NTT
原根
还没有整太明白
待补，丢一个板子
#include<bits/stdc++.h>
#define swap(a,b) (a^=b,b^=a,a^=b)
using namespace std;
#define LL long long
const int MAXN = 3 * 1e6 + 10, P = 998244353, G = 3, Gi = 332748118;
char buf[1 << 21], * p1 = buf, * p2 = buf;
int N, M, limit = 1, L, r[MAXN];
LL a[MAXN], b[MAXN];
inline LL fastpow(LL a, LL k) {
LL base = 1;
while (k) {
if (k & 1) base = (base * a) % P;
a = (a * a) % P;
k >>= 1;
}
return base % P;
}
inline void NTT(LL* A, int type) {
for (int i = 0; i < limit; i++)
if (i < r[i]) swap(A[i], A[r[i]]);
for (int mid = 1; mid < limit; mid <<= 1) {
LL Wn = fastpow(type == 1 ? G : Gi, (P - 1) / (mid << 1));
for (int j = 0; j < limit; j += (mid << 1)) {
LL w = 1;
for (int k = 0; k < mid; k++, w = (w * Wn) % P) {
int x = A[j + k], y = w * A[j + k + mid] % P;
A[j + k] = (x + y) % P,
A[j + k + mid] = (x - y + P) % P;
}
}
}
}
int main() {
scanf("%d%d", &N, &M);
for (int i = 0; i <= N; i++) scanf("%d", a + i);
for (int i = 0; i <= M; i++) scanf("%d", b + i);
while (limit <= N + M) limit <<= 1, L++;
for (int i = 0; i < limit; i++) r[i] = (r[i >> 1] >> 1) | ((i & 1) << (L - 1));
NTT(a, 1); NTT(b, 1);
for (int i = 0; i < limit; i++) a[i] = (a[i] * b[i]) % P;
NTT(a, -1);
LL inv = fastpow(limit, P - 2);
for (int i = 0; i <= N + M; i++)
printf("%d ", (a[i] * inv) % P);
return 0;
}
2.数据结构
线段树
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn = 1e6 + 10;
struct Node {
int l, r, sum, lz;
}T[maxn << 2];
void push_up(int o) {
T[o].sum = T[o << 1].sum + T[o << 1 | 1].sum;
}
void build(int o, int L, int R) {
T[o] = Node{ L,R,0,0 };
if (L == R) {
cin >> T[o].sum;
return;
}
int mid = L + R >> 1;
build(o << 1, L, mid);
build(o << 1 | 1, mid + 1, R);
push_up(o);
}
void push_down(int o) {
if (!T[o].lz)return;
T[o << 1].lz += T[o].lz;
T[o << 1 | 1].lz += T[o].lz;
T[o << 1].sum += (T[o << 1].r - T[o << 1].l + 1) * T[o].lz;
T[o << 1 | 1].sum += (T[o << 1 | 1].r - T[o << 1 | 1].l + 1) * T[o].lz;
T[o].lz = 0;
}
void updt(int o, int l, int r, int z) {
if (l <= T[o].l && T[o].r <= r) {
T[o].lz += z;
T[o].sum += z * (T[o].r - T[o].l + 1);
return;
}
push_down(o);
int mid = T[o].l + T[o].r >> 1;
if (l <= mid) updt(o << 1, l, r, z);
if (r > mid) updt(o << 1 | 1, l, r, z);
push_up(o);
}
int query(int o, int l, int r) {
if (l <= T[o].l && T[o].r <= r) {
return T[o].sum;
}
push_down(o);
int sum = 0, mid = T[o].l + T[o].r >> 1;
if (l <= mid)sum += query(o << 1, l, r);
if (r > mid)sum += query(o << 1 | 1, l, r);
return sum;
}
/*
* @Author: zhl
* @Date: 2020-10-13 20:09:58
*/
#include<bits/stdc++.h>
#define int long long
#define lo (o<<1)
#define ro (o<<1|1)
#define mid (l+r>>1)
using namespace std;
const int N = 2e6 + 10;
int sum[N], lz[N];
void build(int o, int l, int r) {
if (l == r) {
scanf("%lld", &sum[o]);
return;
}
build(lo, l, mid);
build(ro, mid + 1, r);
sum[o] = sum[lo] + sum[ro];
}
int x, y, z;
void push_down(int o, int l, int r) {
if (!lz[o])return;
lz[lo] += lz[o]; lz[ro] += lz[o];
sum[lo] += (mid - l + 1) * lz[o];
sum[ro] += (r - mid) * lz[o];
lz[o] = 0;
}
void updt(int o, int l, int r) {
if (x <= l and r <= y) {
lz[o] += z;
sum[o] += z * (r - l + 1);
return;
}
push_down(o, l, r);
if (x <= mid) updt(lo, l, mid);
if (y > mid) updt(ro, mid + 1, r);
sum[o] = sum[lo] + sum[ro];
}
int query(int o, int l, int r) {
if (x <= l and r <= y) {
return sum[o];
}
push_down(o, l, r);
int ans = 0;
if (x <= mid) ans += query(lo, l, mid);
if (y > mid) ans += query(ro, mid + 1, r);
return ans;
}
int n, m;
signed main() {
scanf("%lld%lld", &n, &m);
build(1, 1, n);
for (int i = 1; i <= m; i++) {
int op; scanf("%lld", &op);
if (op == 1) {
scanf("%lld%lld%lld", &x, &y, &z);
updt(1, 1, n);
}
else {
scanf("%lld%lld", &x, &y);
printf("%lld\n", query(1, 1, n));
}
}
}
树状数组
int lowbit(int i){
return i&(-i);
}
void insert(int ind,int val){
while(ind <= n){
C[ind] += val;
ind += lowbit(ind);
}
}
int query(int n){ //sum of A[1] + A[2] + ... + A[n]
int sum = 0;
while(n){
sum += C[n];
n -= lowbit(n);
}
return sum;
}
LCA倍增
#include<bits/stdc++.h>
#define repE(i,u) for(int i = head[u];i;i = E[i].next)
using namespace std;
const int N = 1e6 + 10;
int f[N][32];
int dep[N];
struct Edge {
int to, next;
}E[N << 1];
int head[N], tot;
void addEdge(int from, int to) {
E[++tot] = Edge{ to,head[from] };
head[from] = tot++;
}
void init(int u, int p) {
dep[u] = dep[p] + 1;
f[u][0] = p;
for (int x = 1; (1 << x) < dep[u]; x++) {
f[u][x] = f[f[u][x - 1]][x - 1];
}
repE(i, u) {
if (E[i].to == p)continue;
init(E[i].to, u);
}
}
int LCA(int x, int y) {
if (dep[x] < dep[y])swap(x, y);
while (dep[x] != dep[y]) {
int u = dep[x] - dep[y];
int v = 0;
while (!(u & (1 << v)))v++;
x = f[x][v];
}
while (x != y) {
int v = 0;
while (f[x][v] != f[y][v])v++;
x = f[x][max(0,v - 1)]; y = f[y][max(0,v - 1)];
}
return x;
}
int n, m, root;
int main() {
scanf("%d%d%d", &n, &m, &root);
for (int i = 1; i < n; i++) {
int x, y; scanf("%d%d", &x, &y);
addEdge(x, y);
addEdge(y, x);
}
init(root, 0);
for (int i = 1; i <= m; i++) {
int x, y; scanf("%d%d", &x, &y);
printf("%d\n", LCA(x, y));
}
}
ST表
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int f[N][32];
int A[N];
int n, m, x, y;
void init() {
for (int i = 1; i <= n; i++) {
f[i][0] = A[i];
}
for (int j = 1; (1 << j) <= n; j++) {
for (int i = 1; i + (1 << j) - 1 <= n; i++) {
f[i][j] = max(f[i][j - 1], f[i + (1 << (j-1))][j - 1]);
}
}
}
int query(int l, int r) {
int k = log2(r - l + 1);
return max(f[l][k], f[r - (1 << k) + 1][k]);
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
scanf("%d", A + i);
}
init();
for (int i = 1; i <= m; i++) {
scanf("%d%d", &x, &y);
printf("%d\n", query(x, y));
}
}
主席树
/*
* @Author: zhl
* @Date: 2020-10-12 19:34:06
*/
#include<bits/stdc++.h>
#define rep(i,a,b) for(int i = a;i <= b;i++)
#define mid (l+r>>1)
using namespace std;
const int N = 5e5 + 10;
int L[N << 5], R[N << 5], sum[N << 5];
int tot;
int build(int l, int r) {
int u = ++tot;
sum[u] = 0;
if (l < r) {
L[u] = build(l, mid);
R[u] = build(mid + 1, r);
}
return u;
}
int insert(int pre, int l, int r, int pos) {
int u = ++tot;
L[u] = L[pre];
R[u] = R[pre];
sum[u] = sum[pre] + 1;
if (l >= r)return u;
if (pos <= mid) {
L[u] = insert(L[pre], l, mid, pos);
}
else {
R[u] = insert(R[pre], mid + 1, r, pos);
}
return u;
}
int query(int rt_x, int rt_y, int l, int r, int k) {
if (l == r) {
return r;
}
int num = sum[L[rt_y]] - sum[L[rt_x]];//区间内，左半区间的数的数量
if (num >= k) {
//在左边
return query(L[rt_x], L[rt_y], l, mid, k);
}
else {
return query(R[rt_x], R[rt_y], mid + 1, r, k - num);
}
}
int n, m;
int A[N], id[N], root[N];
int main() {
cin >> n >> m;
rep(i, 1, n) {
cin >> A[i];
id[i] = A[i];
}
sort(id + 1, id + 1 + n);
int cntID = unique(id + 1, id + 1 + n) - id - 1;
root[0] = build(1, cntID);
rep(i, 1, n) {
int pos = lower_bound(id + 1, id + 1 + cntID, A[i]) - id;
root[i] = insert(root[i - 1], 1, cntID, pos);
}
rep(i, 1, m) {
int x, y, k;
cin >> x >> y >> k;
int pos = query(root[x - 1], root[y], 1, cntID, k);
cout << id[pos] << endl;
}
}
可持久化01Tire
/*
* @Author: zhl
* @Date: 2020-10-13 09:46:47
*/
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i = a;i <= b;i++)
#define repE(i,u) for(int i = head[u];i;i = E[i].next)
#define swap(a,b) a^=b,b^=a,a^=b
const int N = 2e6 + 10;
//cnm 1e6 一直T
//N 5e5,m 5e5
const int maxbit = 30;
struct {
int root[N], c[N][2], tot;
void init() {
c[0][0] = c[0][1] = 0;
tot = 0;
root[0] = 0;
}
int getnode() {
tot++;
c[tot][0] = c[tot][1] = 0;
return tot;
}
//root[v] = insret(Tire.root[v-1], v, val);
int insert(int pre, int v, int val) {
int u = getnode();
int ans = u;
for (int i = maxbit; i >= 0; i--) {
c[u][0] = c[pre][0];
c[u][1] = c[pre][1];
int x = val & (1 << i) ? 1 : 0;
c[u][x] = getnode();
u = c[u][x];
pre = c[pre][x];
}
return ans;
}
int query(int l, int r, int x) {
int MinID = root[l];
int u = root[r];
int ans = 0;
for (int i = maxbit; i >= 0; i--) {
int now = (x & (1 << i)) ? 0 : 1;
if (c[u][now] and c[u][now] >= MinID) {
u = c[u][now];
ans += (1 << i);
}
else {
u = c[u][now ^ 1];
}
}
return ans;
}
}Tire;
int n, m, l, r, x;
int A[N];
int main() {
scanf("%d%d", &n, &m);
Tire.init();
for (int i = 1; i <= n; i++) {
scanf("%d", A + i);
Tire.root[i] = Tire.insert(Tire.root[i-1],i,A[i]);
}
for (int i = 1; i <= m; i++) {
scanf("%d%d%d", &x, &l, &r);
printf("%d\n", Tire.query(l + 1, r + 1, x));
}
}
/*
3 1
1 2 3
*/
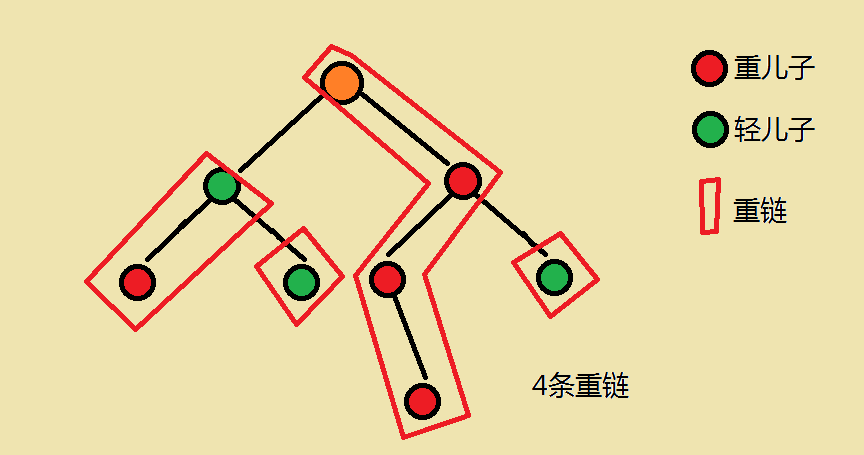
树链剖分
/*
* @Author: zhl
* @Date: 2020-10-13 20:36:59
*/
#include<bits/stdc++.h>
#define rep(i,a,b) for(int i = a;i <= b;i++)
#define repE(i,u) for(int i = head[u];i;i = E[i].next)
#define mid (l+r>>1)
#define lo (o<<1)
#define ro (o<<1|1)
using namespace std;
const int N = 4e5 + 10;
int A[N];
int n, m, root, mod;
struct Edge {
int to, next;
}E[N << 1];
int head[N], tot;
void addEdge(int from, int to) {
E[++tot] = Edge{ to,head[from] };
head[from] = tot++;
}
int fa[N], sz[N], Tfa[N], dep[N], son[N];
//dfs1处理dep,sz,fa,son(重儿子)
void dfs1(int u, int p) {
fa[u] = p;
dep[u] = dep[p] + 1;
sz[u] = 1;
int mx = -1;
repE(i, u) {
int v = E[i].to;
if (v == p)continue;
dfs1(v, u);
sz[u] += sz[v];
if (sz[v] > mx)mx = sz[v], son[u] = v;
}
}
int cnt;
int id[N], val[N], top[N];
//dfs2 剖分数链
void dfs2(int u, int topf) {
id[u] = ++cnt;
val[cnt] = A[u];
top[u] = topf;
if (!son[u])return;
dfs2(son[u], topf);
repE(i, u) {
int v = E[i].to;
if (v == fa[u] or v == son[u])continue;
dfs2(v, v);
}
}
int sum[N << 2], lz[N << 2];
int x, y, z;
void push_down(int o, int l, int r) {
if (!lz[o])return;
lz[lo] += lz[o];
lz[ro] += lz[o];
sum[lo] = (sum[lo] + lz[o] * (mid - l + 1)) % mod;
sum[ro] = (sum[ro] + lz[o] * (r - mid)) % mod;
lz[o] = 0;
}
void build(int o, int l, int r) {
if (l == r) {
sum[o] = val[l];
return;
}
build(lo, l, mid);
build(ro, mid + 1, r);
sum[o] += sum[lo] + sum[ro];
}
void updt(int o, int l, int r) {
if (x <= l and r <= y) {
lz[o] = (lz[o] + z) % mod;
sum[o] = (sum[o] + z * (r - l + 1)) % mod;
return;
}
push_down(o, l, r);
if (x <= mid)updt(lo, l, mid);
if (y > mid)updt(ro, mid + 1, r);
sum[o] = (sum[lo] + sum[ro]) % mod;
}
int query(int o, int l, int r) {
if (x <= l and r <= y) {
return sum[o];
}
int ans = 0;
push_down(o, l, r);
if (x <= mid)ans = (ans + query(lo, l, mid)) % mod;
if (y > mid)ans = (ans + query(ro, mid + 1, r)) % mod;
return ans;
}
int query_path(int a, int b) {
int ans = 0;
while (top[a] != top[b]) {
if (dep[top[a]] < dep[top[b]])swap(a, b);
x = id[top[a]]; y = id[a];
ans = (ans + query(1, 1, cnt)) % mod;
a = fa[top[a]];
}
if (dep[a] > dep[b])swap(a, b);
x = id[a]; y = id[b];
ans = (ans + query(1, 1, cnt)) % mod;
return ans;
}
void updt_path(int a, int b, int k) {
k %= mod;
while (top[a] != top[b]) {
if (dep[top[a]] < dep[top[b]])swap(a, b);
x = id[top[a]]; y = id[a]; z = k;
updt(1, 1, cnt);
a = fa[top[a]];
}
if (dep[a] > dep[b])swap(a, b);
x = id[a]; y = id[b]; z = k;
updt(1, 1, cnt);
}
int main() {
scanf("%d%d%d%d", &n, &m, &root, &mod);
for (int i = 1; i <= n; i++)scanf("%d", A + i);
for (int i = 1; i < n; i++) {
scanf("%d%d", &x, &y);
addEdge(x, y); addEdge(y, x);
}
dfs1(root, 0);
dfs2(root, root);
build(1, 1, cnt);
while (m--) {
int op; scanf("%d", &op);
int a, b, c;
if (op == 1) {//a,b 路径 + c
scanf("%d%d%d", &a, &b, &c);
updt_path(a, b, c);
}
if (op == 2) {//a,b 路径sum
scanf("%d%d", &a, &b);
printf("%d\n", query_path(a, b));
}
if (op == 3) {//a的subtree + c
scanf("%d%d", &a, &c);
x = id[a]; y = id[a] + sz[a] - 1;
z = c;
updt(1, 1, cnt);
}
if (op == 4) {
scanf("%d", &a);
x = id[a]; y = id[a] + sz[a] - 1;
printf("%d\n", query(1, 1, cnt));
}
}
}
/*
5 50 2 24000
7 3 7 8 0
1 2
1 5
3 1
4 1
*/
单调队列(滑动窗口)
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
deque<int>dq;
vector<int>ans;
int n = nums.size();
for(int i = 0;i < n;i++){
if(!dq.empty() && dq.front() == i - k)dq.pop_front();
while(!dq.empty() && nums[dq.back()] < nums[i]) dq.pop_back();
dq.push_back(i);
if(i >= k - 1) ans.push_back(nums[dq.front()]);
}
return ans;
}
};
\(deque\) 里存的是数组的下标
单调栈
3.图论
最短路算法
Dijkstra
复杂度： \(O(VlgV+E)\)
struct Node {
long long d;
int u;
bool operator < (const Node& rhs)const {
//rhs，right-hand-side
return d > rhs.d;
}
};
void dijkstra(int s) {
priority_queue<Node>Q;
for (int i = 1;i <= n;i++) {
d[i] = INF;
}
d[s] = 0;
memset(vis, 0, sizeof(vis));
Q.push(Node{ 0,s });
while (!Q.empty()) {
Node x = Q.top();Q.pop();
int u = x.u;
if (vis[u]) {
continue;
}
vis[u] = 1;
for (int i = 0;i < G[u].size();i++) {
Edge e = edges[G[u][i]];
if (d[e.to] > d[u] + e.dist) {
d[e.to] = d[u] + e.dist;
p[e.to] = G[u][i];
Q.push(Node{ d[e.to],e.to });
}
}
}
}
bellman-ford
复杂度 ： \(O(EV)\)
struct E {
int from, to, w;
}Edges[maxm];
int dis[maxn];
int n, m, s;
bool bellman_ford(int s) {
for (int i = 1; i < n; i++) {
for (int j = 0; j < m; j++) {
int f = Edges[j].from, t = Edges[j].to, w = Edges[j].w;
if (dis[t] > dis[f] + w) {
dis[t] = dis[f] + w;
}
}
}
for (int j = 0; j < m; j++) {
int f = Edges[j].from, t = Edges[j].to, w = Edges[j].w;
if (dis[t] > dis[f] + w) {
return false;
}
}
return true;
}
SPFA
\(O(kE)\) ，\(k\) 为每个节点入队次数
最坏 \(O(EV)\)
void spfa() {
queue<int> q;
memset(dis, 0x3f, sizeof(int) * (n + 10));
memset(vis, 0, sizeof(int) * (n + 10));
q.push(s); dis[s] = 0; vis[s] = 1; //第一个顶点入队，进行标记
while (!q.empty()) {
int u = q.front();
q.pop(); vis[u] = 0;
for (int i = head[u]; ~i; i = E[i].next) {
int v = E[i].to;
if (dis[v] > dis[u] + E[i].w) {
dis[v] = dis[u] + E[i].w;
if (vis[v] == 0) {
//此处判环
//if(++cnt[v] >= n) 有负环
vis[v] = 1;
q.push(v);
}
}
}
}
}
二分图匹配 (匈牙利算法)
#include<iostream>
#include<cstring>
using namespace std;
const int maxn = 505;
int match[maxn];
int G[maxn][maxn];
int vis[maxn];
int n, k;
bool dfs(int u) {
for (int i = 1;i <= n;i++) {
if (G[u][i] && !vis[i]) {
vis[i] = 1;
if (match[i] == 0 || dfs(match[i])) {
match[i] = u;
return true;
}
}
}
return false;
}
int main() {
cin >> n >> k;
int a, b;
for (int i = 0;i < k;i++) {
cin >> a >> b;
G[a][b] = 1;
}
int cnt = 0;
for (int i = 1;i <= n;i++) {
memset(vis, 0, sizeof(vis));
if (dfs(i))
cnt++;
}
cout << cnt;
}
网络流
Dinic
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn = 5e5 + 10;
const int inf = 0x3f3f3f3f3f3f3f3f;
int n, m, s, t, tot, head[maxn];
int ans, dis[maxn], now[maxn];
struct Edge {
int to, next, val;
}E[maxn];
void AddEdge(int from, int to, int w) {
E[tot] = Edge{ to,head[from],w };
head[from] = tot++;
E[tot] = Edge{ from,head[to],0 };
head[to] = tot++;
}
int bfs() {
for (int i = 1; i <= n; i++) dis[i] = inf;
queue<int>Q;
Q.push(s);
dis[s] = 0;
now[s] = head[s];
while (!Q.empty()) {
int u = Q.front();
Q.pop();
for (int i = head[u]; ~i; i = E[i].next) {
int v = E[i].to;
if (E[i].val > 0 && dis[v] == inf) {
Q.push(v);
dis[v] = dis[u] + 1;
now[v] = head[v];
if (v == t)return 1; //分层成功
}
}
}
return 0;
}
int dfs(int x, int sum) {
if (x == t)return sum;
int k, res = 0;
for (int i = now[x]; ~i && sum; i = E[i].next) {
now[x] = i;
int v = E[i].to;
if (E[i].val > 0 && (dis[v] == dis[x] + 1)) {
k = dfs(v, min(sum, E[i].val));
if (k == 0) dis[v] = inf;
E[i].val -= k;
E[i ^ 1].val += k;
res += k;
sum -= k;
}
}
return res;
}
signed main() {
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
cin >> n >> m >> s >> t;
memset(head, -1, sizeof(int) * (n + 10));
for (int i = 1; i <= m; i++) {
int f, t, w;
cin >> f >> t >> w;
AddEdge(f, t, w);
}
while (bfs()) {
ans += dfs(s, inf);
}
cout << ans << endl;
}
最小费用最大流
MCMF
#include<bits/stdc++.h>
using namespace std;
const int maxn = 5e3 + 10;
const int maxm = 5e4 + 10;
struct E {
int to, dis, flow, next;
}e[maxm<<1];
int tot, head[maxn];
void addEdge(int from, int to, int flow, int dis) {
e[tot] = E{ to, dis, flow,head[from] };
head[from] = tot++;
}
int vis[maxn], dis[maxn], incf[maxn], pre[maxn];
int s, t, n, m;
int maxflow, mincost;
bool spfa() {
queue<int>Q;
memset(dis, 0x3f, sizeof dis);
memset(vis, 0, sizeof vis);
Q.push(s);
dis[s] = 0;
vis[s] = 1;
incf[s] = 1 << 30;
while (!Q.empty()) {
int u = Q.front(); Q.pop();
vis[u] = 0;
for (int i = head[u]; i != -1; i = e[i].next) {
if (!e[i].flow) continue; //没有残余流量
int v = e[i].to;
if (dis[v] > dis[u] + e[i].dis) {
dis[v] = dis[u] + e[i].dis;
incf[v] = min(incf[u], e[i].flow);
pre[v] = i;
if (!vis[v]) vis[v] = 1, Q.push(v);
}
}
}
if (dis[t] == 0x3f3f3f3f)return 0;
return 1;
}
void MCMF() {
while (spfa()) {
int x = t;
maxflow += incf[t];
mincost += dis[t] * incf[t];
while (x != s) {
int p = pre[x];
e[p].flow -= incf[t];
e[p ^ 1].flow += incf[t];
x = e[p ^ 1].to;
}
}
}
signed main() {
scanf("%d%d%d%d", &n, &m, &s, &t);
memset(head, -1, sizeof head);
for (int f, t, w, x, i = 1; i <= m; i++) {
scanf("%d%d%d%d", &f, &t, &w, &x);
addEdge(f, t, w, x);
addEdge(t, f, 0, -x);
}
MCMF();
printf("%d %d\n", maxflow, mincost);
}
一般图匹配（开花算法）
#include<bits/stdc++.h>
using namespace std;
const int maxn = 600;
const int maxm = 400000; //双向边要开两倍！！
struct Edge {
int to, nxt;
}E[maxm];
int head[maxn];
int tot;
int gcd(int x,int y)
{
return y?gcd(y,x%y):x;
}
void addEdge(int from, int to, bool istwo = false) {
E[tot] = Edge{ to,head[from] };
head[from] = tot++;
//双向边
if (istwo) {
E[tot] = Edge{ from,head[to] };
head[to] = tot++;
}
}
int fa[maxn];//并查集
int find(int x) {
return fa[x] == x ? x : fa[x] = find(fa[x]);
}
void merge(int a, int b) {
a = find(a);
b = find(b);
if (a != b) fa[a] = b;
}
int n, m;
int match[maxn];//记录匹配
int Q[maxn], rear;//队列
int nxt[maxn], mark[maxn], vis[maxn];
int LCA(int x, int y) {
static int t = 0; t++;
while (1) {
if (x != -1) {
x = find(x); //点对应到花
if (vis[x] == t)return x;
vis[x] = t;
if (match[x] != -1) x = nxt[match[x]]; // 有匹配，向上走
else x = -1;//停下来
}
swap(x, y);
}
}
void group(int a, int p) {
while (a != p) {
int b = match[a], c = nxt[b];
if (find(c) != p) nxt[c] = b;
if (mark[b] == 2) mark[Q[rear++] = b] = 1;
if (mark[c] == 2) mark[Q[rear++] = c] = 1;
merge(a, b); merge(b, c);
a = c;
}
}
void aug(int s) {
for (int i = 1; i <= n; i++) {
nxt[i] = -1; fa[i] = i; mark[i] = 0; vis[i] = -1;
}
mark[s] = 1;
Q[0] = s; rear = 1;
for (int front = 0; match[s] == -1 && front < rear; front++) {
int x = Q[front];
for (int i = head[x]; i != -1; i = E[i].nxt) {
int y = E[i].to;
if (match[x] == y) continue; // x与y已匹配，忽略
if (find(x) == find(y)) continue; // x与y同在一朵花，忽略
if (mark[y] == 2) continue; // 偶环，忽略
if (mark[y] == 1) { // 缩点
int r = LCA(x, y); //
if (find(x) != r) nxt[x] = y;
if (find(y) != r) nxt[y] = x;
group(x, r);
group(y, r);
}
else if (match[y] == -1) { // y自由，可以增广
nxt[y] = x;
for (int u = y; u != -1; ) { // 交叉链取反
int v = nxt[u];
int mv = match[v];
match[v] = u, match[u] = v;
u = mv;
}
break; // 搜索成功，退出循环将进入下一阶段
}
else {
nxt[y] = x;
mark[Q[rear++] = match[y]] = 1;
mark[y] = 2;
}
}
}
}
void init() {
memset(head, -1, sizeof head);
}
int main() {
scanf("%d",&n);
init();
for(int i = 1;i <= n;i++){
for(int j = 1;j <= i;j++){
if(gcd(i,j) != 1){
addEdge(i,j,true);
}
}
}
for (int i = 1; i <= n; i++) {
match[i] = -1;
}
for (int i = 1; i <= n; i++) {
if (match[i] == -1) aug(i);
}
int tot = 0;
for (int i = 1; i <= n; i++) {
if (match[i] != -1)tot++;
else match[i] = 0;
}
printf("%d\n", tot>>1);
memset(vis,0,sizeof vis);
for (int i = 1; i <= n; i++) {
if(vis[i])continue;
printf("%d %d%s", i, match[i], i == n ? "\n" : " ");
vis[i] = 1;vis[match[i]] = 1;
}
}
树的重心
void getroot(int u, int f) { //f 是 father 节点
// 找质心
sz[u] = 1;
int mxchild = 0; //子树的最大节点数
for(int i = head[u]; i != -1; i = e[i].nxt ) {
int v = e[i].to;
if(v != f && !visit[v]) {
getroot(v, u);
sz[u] += sz[v];
mxchild = max(mxchild, sz[v]);
}
}
int tmp = max(mxchild, subtreesize - sz[u]); //父子树的最大节点个数
if(tmp < nowmn) {
nowmn = tmp;
rt = u;
}
}
树的直径
int dfs(int u,int pre){
int maxpath = 0;
for(int v : adj[u]){
if(v == pre)continue;
dep[v] = dep[u] + 1;
int nowpath = 1 + dfs(v,u);
d = max(d,nowpath + maxpath); //d 是树的直径
maxpath = max(maxpath,nowpath);
}
return maxpath;
}
4.字符串
KMP
int kmp(){
int i = 0,j = 0;
while(i < n){ // m 是匹配串的长度
if(j == - 1 || s[i] == p[j]){
j++;
i++;
if(j == m){
return i - j + 1;
}
}
else{
j = next[j];
}
}
return -1; //没有找到匹配的子串
}
void get_next(){
next[0] = -1;
int k = -1;
int j = 0;
while(j < m){
if(k == -1 || p[k] == p[j]){
k++;j++;
next[j] = k;
}
else{
k = next[k];
}
}
}
Manacher
/*
* @Author: zhl
* @Date: 2020-10-14 11:36:53
*/
class Solution {
public:
string longestPalindrome(string s) {
int n = s.length();
if(n < 2)return s;
string t = "$";
for(int i = 0;i < n;i++){
t += "#"+s.substr(i,1);
}
t += "#@";
n = t.length();
vector<int>p;p.resize(n+10);
int id = 0,mx = 0;int maxlen = 0,cen = 0;
for(int i = 1;i < n - 1;i++){
p[i] = i < mx ? min(mx-i,p[2*id-i]) : 1;
while(t[i-p[i]] == t[i+p[i]])p[i]++;
if(i+p[i]>mx){
mx = i+p[i];
id = i;
}
if(p[i] - 1 > maxlen){
maxlen = p[i]-1;
cen = i;
}
}
int st = (cen - maxlen)/2;
return s.substr(st,maxlen);
}
};
AC自动机
#include<bits/stdc++.h>
using namespace std;
const int N = 6e6 + 10;
queue<int>q;
struct {
int c[N][26], fail[N], val[N], cnt;
void insert(char* s) {
int len = strlen(s); int now = 0;
for (int i = 0; i < len; i++) {
int v = s[i] - 'a';
if (!c[now][v])c[now][v] = ++cnt;
now = c[now][v];
}
val[now]++;
}
void getFail() {
for (int i = 0; i < 26; i++) {
if (c[0][i])fail[c[0][i]] = 0, q.push(c[0][i]);
}
while (!q.empty()) {
int u = q.front(); q.pop();
for (int i = 0; i < 26; i++) {
if (c[u][i]) {
fail[c[u][i]] = c[fail[u]][i];
q.push(c[u][i]);
}
else c[u][i] = c[fail[u]][i];
}
}
}
int query(char* s) {
int len = strlen(s); int now = 0, ans = 0;
for (int i = 0; i < len; i++) {
now = c[now][s[i] - 'a'];
for (int t = now; t && val[t] != -1; t = fail[t]) {
ans += val[t];
val[t] = -1;
}
}
return ans;
}
}Ac;
int n;
char p[N];
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%s", p);
Ac.insert(p);
}
Ac.getFail();
scanf("%s", p);
printf("%d\n", Ac.query(p));
}
最小表示法
5.计算几何
const double eps = 1e-8;
const double inf = 1e20;
const double pi = acos(-1.0);
int sgn(double x) {
if (fabs(x) < eps)return 0;
if (x < 0) return -1;
else return 1;
}
struct Point {
double x, y;
Point() {}
Point(double _x, double _y) {
x = _x;
y = _y;
}
void input() { scanf("%lf%lf", &x, &y); }
void output() { printf("%.2f %.2f\n", x, y); }
bool operator == (Point b)const {
return sgn(x - b.x) == 0 and sgn(y - b.y) == 0;
}
bool operator <(const Point& b)const {
//左下小
return sgn(x - b.x) == 0 ? sgn(y - b.y) < 0 : x < b.x;
}
Point operator -(const Point& b)const {
return Point{ x - b.x,y - b.y };
}
double operator ^(const Point& b)const {
//叉积
return x * b.y - y*b.x;
}
double operator *(const Point& b)const {
return x * b.x + y * b.y;
}
double len() {
return sqrt(x * x + y * y);
//return hypot(x, y);
}
double len2() {
return x * x + y * y;
}
double distance(Point p) {
return sqrt((x-p.x)*(x-p.x)+(y-p.y)*(y-p.y));
//return hypot(x - p.x, y - p.y);
}
Point operator +(const Point& b)const {
return Point{ x + b.x, y + b.y };
}
Point operator *(const double& k)const {
return Point{ x * k, y * k };
}
Point operator /(const double& k)const {
return Point{ x / k, y / k };
}
double rad(Point a, Point b) {
Point p = *this;
return fabs(atan2(fabs((a - p) ^ (b - p)),((a - p) * (b - p))));
}
Point rotleft() {
return Point{ -y,x };
}
//顺时针旋转 90 度
Point rotright() {
return Point{ y, -x };
}
//绕着 p 点逆时针旋转 angle
Point rotate(Point p, double angle) {
Point v = (*this) - p;
double c = cos(angle), s = sin(angle);
return Point{ p.x + v.x * c - v.y * s, p.y + v.x * s + v.y * c };
}
};
struct Line {
Point s, e;
bool operator == (Line v) {
return s == v.s and e == v.e;
}
Line() {}
Line(Point _s, Point _e) {
s = _s;
e = _e;
}
Line(Point p, double angle) {
s = p;
if (sgn(angle - pi / 2) == 0) {
e = s + Point{ 0,1 };
}
else {
e = s + Point{ 1,tan(angle) };
}
}
//ax + by + c = 0;
Line(double a, double b, double c) {
if (sgn(a) == 0) {
s = Point{ 0,-c / b };
e = Point{ 1,-c / b };
}
else if (sgn(b) == 0) {
s = Point{ -c / a, 0 };
e = Point{ -c / a, 1 };
}
else {
s = Point{ 0,-c / b };
e = Point{ 1,(-c - a) / b };
}
}
void input() {
s.input();//start
e.input();//end
}
void adjust() {
if (e < s)swap(s, e);
}
double length() {
return s.distance(e);
}
double angle() {
double k = atan2(e.y - s.y, e.x - s.x);
if (sgn(k) < 0) k += pi;
if (sgn(k - pi) == 0) k -= pi;
return k;
}
//1 left
//2 right
//3 on line
int relation(Point p) {
int c = sgn((p - s) ^ (e - s));
if (c < 0)return 1;
else if (c > 0)return 2;
else return 3;
}
bool pointOnSeg(Point p) {
return sgn((p - s) ^ (e - s)) == 0 and sgn((p - s) * (e - s)) <= 0;
}
bool parallel(Line v) {
return (sgn((e - s) ^ (v.e - v.s)) == 0);
}
//seg cross seg
//2 规范相交
//1 非规范相交
//0 不相交
int segCrossSeg(Line v) {
int d1 = sgn((e - s) ^ (v.s - s));
int d2 = sgn((e - s) ^ (v.e - s));
int d3 = sgn((v.e - v.s) ^ (s - v.s));
int d4 = sgn((v.e - v.s) ^ (e - v.s));
if ((d1 ^ d2) == -2 and (d3 ^ d4) == -2)return 2;//-2 = (-1)^1
return (d1 == 0 and sgn((v.s - s) * (v.s - e)) <= 0) or
(d2 == 0 and sgn((v.e - s) * (v.e - e)) <= 0) or
(d3 == 0 and sgn((s - v.s) * (s - v.e)) <= 0) or
(d4 == 0 and sgn((e - v.s) * (e - v.e)) <= 0);
}
//Line cross seg
//2 规范相交
//1 非规范相交
//0 不相交
int lineCrossSeg(Line v) {
int d1 = sgn((e - s) ^ (v.s - s));
int d2 = sgn((e - s) ^ (v.e - s));
if ((d1 ^ d2) == -2)return 2;
return(d1 == 0 or d2 == 0);
}
//Line cross Line
//2 相交
//1 重合
//0 平行
int lineCrossLine(Line v) {
if (this->parallel(v))
return v.relation(s) == 3;
return 2;
}
//求两直线的交点
Point crossPoint(Line v) {
double a1 = (v.e - v.s) ^ (s-v.s);
double a2 = (v.e-v.s) ^ (e-v.s);
return Point{ (s.x * a2 - e.x * a1) / (a2 - a1), (s.y * a2 - e.y * a1) / (a2 - a1) };
}
//点到直线的距离
double disPointToLine(Point p) {
return fabs((p - s) ^ (e - s)) / length();
}
//点到线段的距离
double disPointToSeg(Point p) {
if (sgn((p - s) * (e - s)) < 0 or sgn((e - s) * (s - e)) < 0)
return min(p.distance(s), p.distance(e));
return disPointToLine(p);
}
//线段到线段的距离
double disSegToSeg(Line v) {
return min(min(disPointToSeg(v.s), disPointToSeg(v.e)), min(v
.disPointToSeg(s), v.disPointToSeg(e)));
}
//p 在直线上的投影
Point lineProg(Point p) {
return s + (((e - s) * ((e - s) * (p - s))) / ((e - s).len2()));
}
//p 关于直线对称的点
Point symmetryPoint(Point p) {
Point q = lineProg(p);
return Point{ 2 * q.x - p.x, 2 * q.y - p.y };
}
};
反演
反演
定义
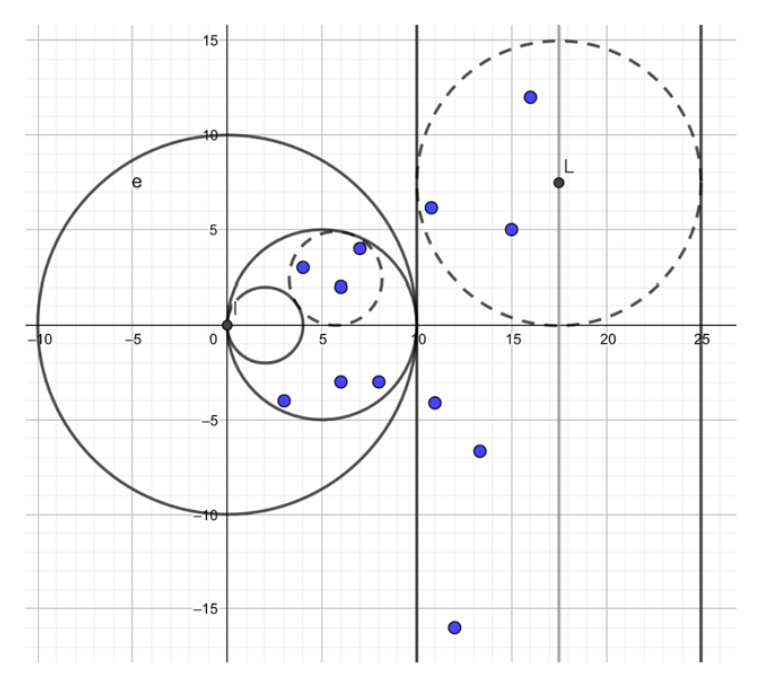
若 \(OP\cdot OP' = r^2\) , 则称 \(P\) 与 \(P'\) 关于 \(O\) 互为反演，反演半径为 \(r\)
该题反演后，转化为很简单的问题
