具身智能

Topic I: 3D VIsion

Topic II: Robotics

Topic IV: Reinforcement learning

Linear Algebra

Vector Space 向量空间

• Linear Combination 线性组合

  \(w=a_1v_1+a_2v_2+...+a_nv_n=\sum_i a_iv_i\)

• Span of Vectors

  \(v_i \in V_m\), \(w \in V_m\)

• Infinite-Ddimensional Vector Space

Optimization Problem

\[min_{x \in \mathbb{R}^n f(x)} \\ s.t. g(x) = 0 \\ h(x) \ge 0 \]

1. Lagrange Multipliers

   \[\nabla f(x)=\lambda\nabla g(x) \\ g(x)=0 \\ \mathcal{L}(x,\lambda) \equiv f(x)+\lambda\cdot g(x) \]

2. PCA (Principle Component Analysis)

Curve

1. Parameterized Curve

   \[\gamma:\mathbb{R}\to\mathbb{R}^{2},\gamma(t)=(x(t),y(t)) \]

2. Reparameterization

   \[\tilde{\gamma}(t):=\gamma(\phi(t)) \\ \tilde{\gamma}^{\prime}(t)=\frac{d}{dt}\gamma(\phi(t))=\mathbf{v}(\phi(t))\phi^{\prime}(t). \]

3. Arc Length

   \[\int_a^b\left\|\gamma'(t)\right\|dt \]

4. Tangent and Nomal (切线、法线)

   \[T'(s) = \mathcal{K}(s) N(s) \\ N'(s) = - \mathcal{K}(s) T(s) \]

5. Curvature (曲率)

   \[\mathcal{r}(s):=\frac{1}{\mathcal{k}(s)} \]

6. 3D Curves

Surface I

Surface II

Representation

• Polygonal Mesh & Triangle Mesh
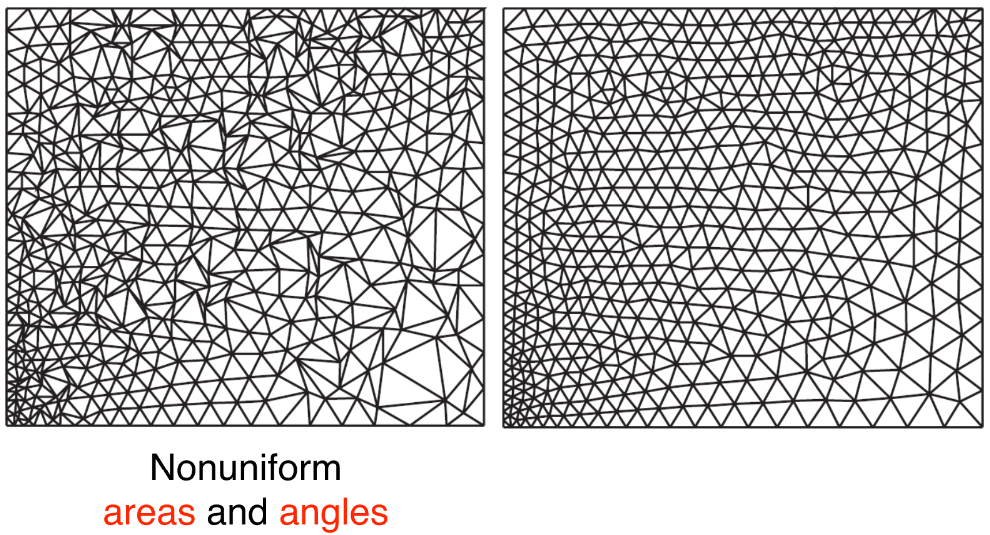
  • Bad Mesh (Nonuniform areas)
    
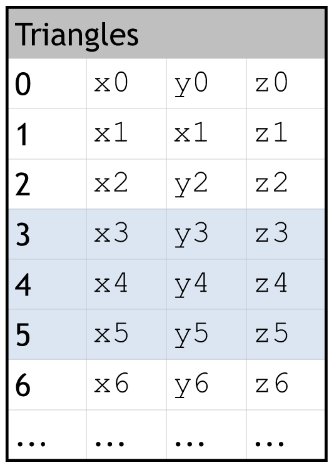
  • Data Structures for Surfaces: Triangle list (STL format)
    
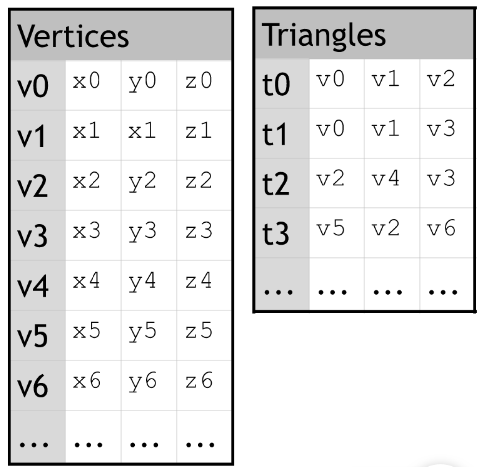
  • Vertex, Face (OBJ format)
    
• Point Cloud
  • Uniform Sampling
  • Farthest Point Sampling
• Voxelization

Transformation

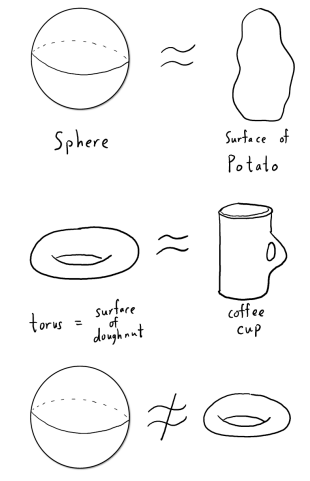
• Topology (拓朴结构)
  
• Orientation: rotation
  • pitch(俯仰角), roll(翻滚角), yaw(偏航角) (rotation in \(\mathbb{R}^3\))

库函数的使用

Mujoco

Basics

xml

<mujoco>  <!--主标签-->
  <worldbody>
    <light name="top" pos="0 0 1"/>
    <geom name="red_box" type="box" size=".2 .2 .2" rgba="1 0 0 1"/>
    <geom name="green_sphere" pos=".2 .2 .2" size=".1" rgba="0 1 0 1"/>
  </worldbody>
</mujoco>

mujoco.MjModel

mjModel中包含模型的几何描述信息（不会随时间改变），如颜色、尺寸等信息

from mujoco import MjModel

xml = """
<mujoco>
  <worldbody>
    <geom name="red_box" type="box" size=".2 .2 .2" rgba="1 0 0 1"/>
    <geom name="green_sphere" pos=".2 .2 .2" size=".1" rgba="0 1 0 1"/>
  </worldbody>
</mujoco>
"""
"""type(model) => mujoco._structs.MjModel"""
model = MjModel.from_xml_string(xml)
model.ngeom  # 获取模型中定义的几何体数量
model.geom_pos   # 获取模型中所有几何体的位置数组 (n, 3)
model.geom_rgba  # 获取所有几何体的颜色数组 (n, 4) 
# n: 几何体数量，4: [r,g,b,a]

"""type(inst) => mujoco._structs._MjModelGeomViews"""
inst = model.geom(<geom_name>)  # 通过名称获取几何体实例（当名称不存在时报错）
inst.rgba  # 获取实例几何体的颜色数组 (4, )
inst.id  # 获取实例几何体的id (int)

# 通过几何体的名称查找id
id = mujoco.mj_name2id(model, mujoco.mjtObj.mjOBJ_GEOM, <geom_name>)
model.geom_rgba[id, :]  # 通过id获取几何体的颜色数组

mujoco.MjData

mjData中包含模型的状态信息，如物体在世界空间中的笛卡尔坐标

from mujoco import MjData
"""type(data) => mujoco._structs.MjData"""
data = mujoco.MjData(model)  # model为上一步创建的mjModel几何体
data.geom_xpos  # model中所有实例几何体的笛卡尔坐标 (n, 3)
"""type(inst) => mujoco._structs._MjDataGeomViews"""
inst = data.geom(<geom_name>)
inst.xpos # 通过名称获取实例几何体的笛卡尔坐标 (3, )
"""
inst的属性：
  id
  name
  xmat
  xpos: 实例几何体的笛卡尔坐标 (3, )
"""

Rendering

import mujoco
import mediapy as media

xml = """
<mujoco>
  <worldbody>
    <light name="top" pos="0 0 1"/>  <!--添加场景灯光-->
    <geom name="red_box" type="box" size=".2 .2 .2" rgba="1 0 0 1"/>
    <geom name="green_sphere" pos=".2 .2 .2" size=".1" rgba="0 1 0 1"/>
  </worldbody>
</mujoco>
"""
model = mujoco.MjModel.from_xml_string(xml)
data = mujoco.MjData(model)

with mujoco.Renderer(model) as renderer:
  mujoco.mj_forward(model, data)  # we should propagate the values in `mjData` using `mujoco.mj_forward(model, data)`
  renderer.update_scene(data)

  media.show_image(renderer.render())

Simulation

Numpy

import numpy as np

np.linalg.solve(A, b)  
# 求解线性方程组 Ax=b
# A：(M,M)的二维系数矩阵
# b：(M,1)的一维数组
# 对于一般的非方阵A，可以构造A^TAx=A^Tb，使用`np.linalg.solve(A^TA, A^Tb)`来求解x