25-0901 DFT 与频谱泄漏

在频谱分析中，经常会遇到一个问题：为什么有时候信号能量只集中在一个频率点，而有时候会“拖尾”，产生频谱泄漏？
要理解这一点，我们从 离散傅里叶变换 (DFT) 的定义出发。

1. 信号模型

考虑一个复指数信号：

$ x[n] = e^{j \tfrac{2\pi}{N} m_0 n}, \quad k=0,1,\dots,N-1 $

其中：

$$m_0$ = 与信号频率对应的“DFT bin”索引，可以是整数或非整数$

$$
X[k] = \sum_{n=0}^{N-1} x[n] e^{-j 2 \pi \tfrac{k}{N} n}, \quad k=0,1,\dots,N-1
$$

对应的频率轴为：

$$
f_k = \frac{k}{N} f_s
$$

即每个 bin 对应的频率间隔是：

$$
\Delta f = \frac{f_s}{N}
$$

$$
X[k] = \sum_{n=0}^{N-1} e^{j 2 \pi \tfrac{(m_0-k)}{N} n}
$$

这是一个有限几何级数，其闭式解为：

$$
X[k] = \frac{1 - e^{j 2\pi (m_0-k)}}{1 - e^{j 2\pi \tfrac{(m_0-k)}{N}}}
$$

进一步化简为 **Dirichlet 核** 形式：

$$
X[k] = e^{j \pi (m_0-k)(N-1)/N} \cdot \frac{\sin(\pi (m_0-k))}{\sin\!\big(\pi (m_0-k)/N\big)}
$$

其幅度为：

$$
|X[k]| = \left| \frac{\sin(\pi (m_0-k))}{\sin(\pi (m_0-k)/N)} \right|
$$

情况 A：m₀为整数（频率正好落在 bin 上）

若m₀ ∈ ℤ，并且我们正好计算长度为

$X[m_0] = N $$

当 $k \neq m₀$ $$e^{j \tfrac{2\pi}{N}(m_0-k)}=1$），所以：$

结论： 整数 bin 时，信号频率与 DFT 栅格完全对齐，能量集中在单个 DFT 点上，无泄漏。

情况 B：m₀不为整数

若 m₀ ∉ ℤ $，那么分子与分母均不为零，结果为：$

　　$$
　　X[k] \neq 0 \quad \forall k
　　$$

结论： 当频率不落在整数 bin 上时，能量会按照 Dirichlet 核的形状分布在所有 DFT 点上，表现为 频谱泄漏：主瓣之外还有一系列旁瓣。

4. 问题：FFT 点数与时域信号长度不一致的情况

在实际频谱分析中，我们常常使用快速傅里叶变换（FFT）来代替 DFT 计算。
此时有一个关键细节：**FFT 的点数 $n_{\text{fft}}$ 通常不等于时域信号长度 $N$ **。

这就引出了一个常见问题：为什么当 $N \neq n_{\text{fft}}$ 时，即便信号频率是整数 bin，对应的频谱结果也可能出现泄漏现象？

4.1 数学分析

设时域信号长度为 $L$（即实际可用样本数），FFT 点数为 $ n_{\text{fft}} $，输入信号为

$$
x[n] = e^{j 2\pi \tfrac{m_0}{n_{\text{fft}}} n}, \quad n=0,1,\dots,L-1
$$

其中 $m_0$ 是相对于 $ n_{\text{fft}} $ 定义的“频率索引”。
把它代入 DFT（注意求和上限是 $L-1$ 而非 $n_{\text{fft}}$）：

$$
X[k] = \sum_{n=0}^{L-1} e^{j 2 \pi \tfrac{(m_0-k)}{n_{\text{fft}}} n}
= \frac{1 - e^{j 2\pi \tfrac{(m_0-k)}{n_{\text{fft}}} L}}{1 - e^{j 2\pi \tfrac{(m_0-k)}{n_{\text{fft}}}}}.
$$

进一步化简为 Dirichlet 核形式：

$$
X[k] = e^{j \pi (m_0-k)(L-1)/n_{\text{fft}}} \cdot \frac{\sin(\pi (m_0-k) L /n_{\text{fft}})}{\sin\!\big(\pi (m_0-k)/n_{\text{fft}}\big)}
$$

4.2 无泄漏的条件

所谓无泄漏（no leakage），是指某个 $k$ 上 $X[k]$ 最大，且在其他频点严格为零。由上述公式可知，需要同时满足以下两个条件：

1. **分子为零**

$$
\frac{(m_0-k)L}{n_{\text{fft}}} \in \mathbb{Z}.
$$

这保证了除了某些特殊点外，其它频点幅度为零。

2. **分母不为零**

$$
\frac{(m_0-k)}{n_{\text{fft}}} \notin \mathbb{Z}.
$$

否则分母为零，公式失效，不能保证有限幅度。

4.3 特殊情况

如果 $n_{\text{fft}} = L/p$（$p$ 为正整数），则条件变为：

$$
\frac{(m_0-k)L}{n_{\text{fft}}} = (m_0-k)p \in \mathbb{Z}.
$$

这意味着只要 $(m_0-k)$ 是 $1/p$ 的整数倍，就可能在某些 bin 上避免泄漏。
例如：当$n_{\text{fft}} = L/2$ 时，$(m_0-k)$ 为半整数也能满足条件。但是缺点是nfft过低会导致频谱分辨率下降。

5. 矩形窗效应与频谱泄漏

另一层原因在于：有限长信号本质上等于**无限长信号与矩形窗相乘**。

* 矩形窗定义：

$$
w[n] =
\begin{cases}
1, & 0 \leq n \leq L-1, \\
0, & \text{otherwise}.
\end{cases}
$$

* 矩形窗的 DTFT：

$$
W(e^{j\omega}) = e^{-j\omega (L-1)/2} \cdot \frac{\sin(\tfrac{\omega L}{2})}{\sin(\tfrac{\omega}{2})}.
$$

它是 **sinc 型函数（Dirichlet 核）**，包含主瓣与无穷多旁瓣。

* 卷积效应：

$$
X_w(e^{j\omega}) = \frac{1}{2\pi}\, \big( X(e^{j\omega}) * W(e^{j\omega}) \big).
$$

因此，即使原始频谱是理想冲激（单一频率），经过矩形窗截断后也会扩散成 Dirichlet 核形状，表现为泄漏。

6.MATLAB代码演示

下面给出一份基础代码，用于比较 矩形窗 与 Hann 窗 在不同 $m_0$ 情形下的频谱结果。注意$m_0$与对应频率$f_0$的关系与采样率fs和nfft有关。

clear;
fs = 8000;       % Sampling frequency (Hz)
t = (0:1000-1)'; % Time sequence (0~999)
L = length(t);

% ----------  nfft  ----------
nfft = L;  % Default setting, can change later
% -----------------------------------

f = (0:nfft-1)' * (fs/nfft);   % Frequency axis
m0_list = [201, 200.7]; % Two test frequencies
f0_list = m0_list * fs / nfft;

% Hann window (with normalization for amplitude correction)
w = hann(L);
w = w / mean(w);

figure;
for idx = 1:2
    m0 = m0_list(idx);
    f0 = f0_list(idx);

    % ----------- Case 1: Rectangular window (no window) -----------
    x_rect = exp(1i*2*pi*m0/nfft * t);

    % DFT by definition
    X_rect = zeros(nfft,1);
    for k = 1:nfft
        for n = 0:L-1
            X_rect(k) = X_rect(k) + x_rect(n+1) * exp(-1i*2*pi*(k-1)/nfft * n);
        end
    end

    % ----------- Case 2: Hann window -----------
    x_hann = x_rect .* w;

    X_hann = zeros(nfft,1);
    for k = 1:nfft
        for n = 0:L-1
            X_hann(k) = X_hann(k) + x_hann(n+1) * exp(-1i*2*pi*(k-1)/nfft * n);
        end
    end

    % ----------- Plot results -----------
    subplot(2,2,(idx-1)*2+1);
    plot(f, 20*log10(abs(X_rect)), 'r','LineWidth',1.2);
    grid on; xlabel('Frequency (Hz)'); ylabel('Magnitude (dB)');
    title(['Rectangular, m0=', num2str(m0), ', f0=', num2str(f0,'%.2f')]);
    xlim([0, fs/2]); ylim([-100,70]);

    subplot(2,2,(idx-1)*2+2);
    plot(f, 20*log10(abs(X_hann)), 'b','LineWidth',1.2);
    grid on; xlabel('Frequency (Hz)'); ylabel('Magnitude (dB)');
    title(['Hann, m0=', num2str(m0), ', f0=', num2str(f0,'%.2f')]);
    xlim([0, fs/2]); ylim([-100,70]);
end

sgtitle('DFT Results with Rectangular vs Hann Window (dB)');

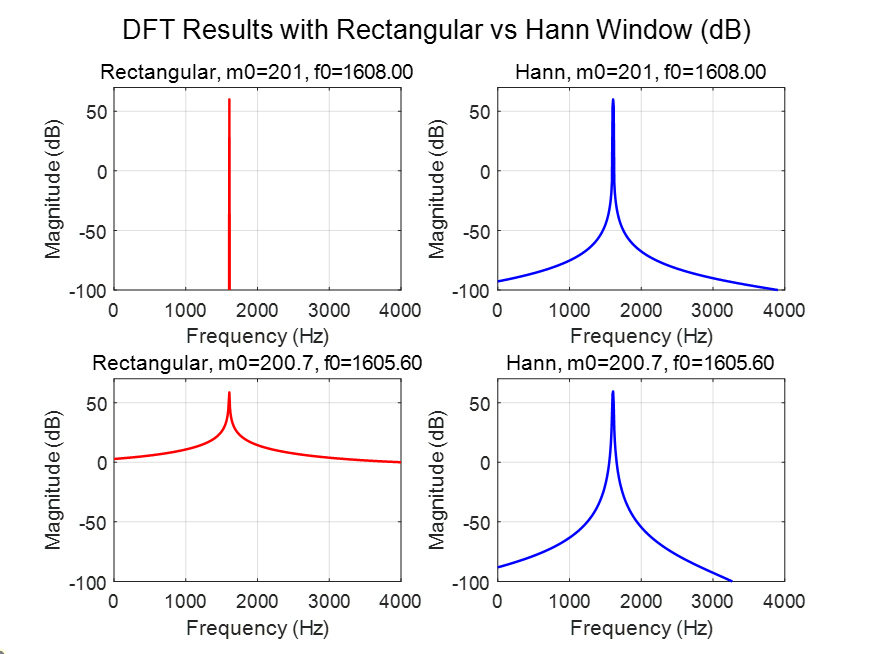
6.1 情况一：$n_{\text{fft}} = L$

即上述代码不变的情况下，

当 $m_0$ 为整数（如 201）时：矩形窗下无泄漏，能量完全集中在单个 bin；
当 $m_0$ 非整数（如 200.7）时：频谱泄漏明显，旁瓣延展；
Hann 窗对整数 bin 情况反而会引入轻微失真，但在泄漏情况下能有效抑制旁瓣。

6.2 情况二：$n_{\text{fft}}$ = 最小的 2 的幂的指数

代码nfft部分做如下修改

nfft = 2^nextpow2(L);  % DFT points, nfft = 1024 in this case

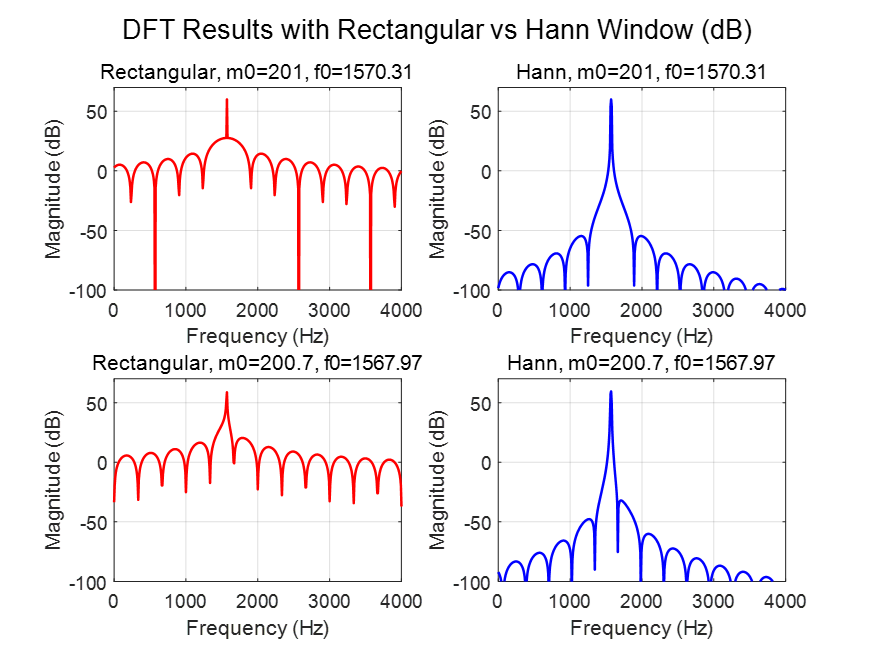
即零填充，把 1000 点信号填充到 1024 点 FFT；对整数 $m_0$（如 201）时，虽然 $m_0$ 对齐了 bin，但由于 $L$ 与$n_{\text{fft}}$ 不同，仍然会出现旁瓣；

这说明零填充只增加了频率采样密度，并不能消除泄漏。

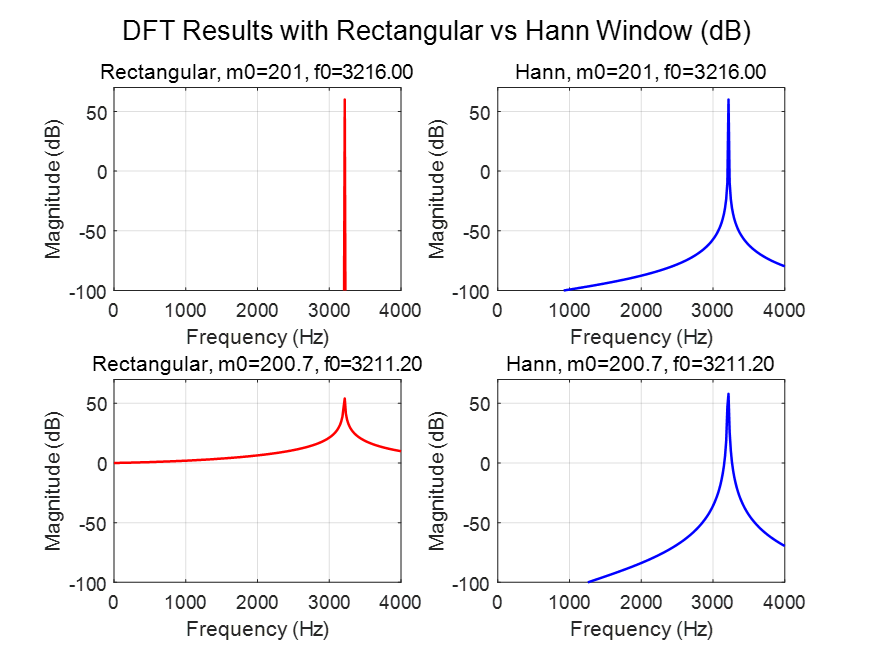
6.3 情况三：$n_{\text{fft}} = L/2$

nfft = L / 2;  % DFT points, nfft = 500 in this case

当 $m_0$ 为整数时（如 201），也能达到抑制旁瓣的效果；

7.总结

频谱无泄露或极少的情况下，如6.1，6.3，加窗（如hann）会导致更多误差；
其他情况下加窗会明显抑制泄露；
6.2情况是大多数，所以加窗很有必要.

posted @ 2025-09-01 10:48 积分三换阅读(10) 评论(0) 收藏举报

刷新页面返回顶部

积分三换