组建一台计算机3_硬件3 多位运算器
前言:
放假有一周的时间,到家也有四五天的时间了,这几天把《code》好好的看了一遍。尽管之前也有草草翻过,但是把时候我就曾告诉自己,无论如何都是要把书中的这些东西都实现一遍的。于是说干就干,这几天基本上就在搞这些东西了。这些学习成果要感谢余富帅给我传的软件以及一些推荐。
=========================================================================
转载请遵循GNU开源宣言。Copyleft ! <2013>, <http://www.cnblogs.com/sciencefans from buaa 华罗庚班>
阅读此文,你需要拥有以下基础:
1.小学代数相关知识;2.初中电路;3.高中门电路相关知识;4.本系列之前两节的内容;5.二进制和十进制的转换(这一点不会也没有关系)。
之前已经做好了一个对位加法器,对于减法和负数的运算支持的不是很好。所以现在应该研究一下负数和减法运算应该如何实现。
在解决这个问题之前,会遇到另一个问题:我们日常生活中,想表达一个负数是很自然的事情:-2,-33.2,-10等等。但是在计算机里可不是这么容易。首先他没有‘-’这个符号,它所能接受,处理以及存储的东西只有两个——0和1.我们在大学生计算机基础课上学过:在机器中的数字用补码的形式存储。但是当时没有人深究它的原因也没有人思考前辈们是如何想到用补码来存储一个数字的。非常巧,这个问题在研究减法运算的时候解决了。
如果想表示一个负数,那么应该用某一个位来表示正负。既然我们通常爱把正负号放在数字的最左端,那么何不把一个对位(这里以8位举例)的最左端的那个位的0,1状态定位正,负的表达呢?但这意味着能表示的数的绝对值范围缩减了一半,但是为了能达到负数的表示,这样做是值得的——大不了把机器字长再扩大一倍。
如果现在想计算253-176是多少,也就是在计算1111 1101 – 1011 0000.
不难发现253 – 176 = 253 + ((255 - 176)+ 1) – 256。
先不用想为什么要这样变换,马上就会明白。
化成二进制之后就变成:1111 1101 + ((1111 1111 – 1011 0000) + 0000 0001) – 1 0000 0000
首先计算括号里的。非常明显,1111 1111 – 1011 0000这一步是在对1011 0000取反。那么我们用一个取反器就可以实现(8位取反器也就是8个(甚至可以压缩至一个)非门的并联)。最后一个减法是9位运算,只需要使之前运算的第九个进位溢出抛弃即可(当然也可以存下来)。而其他的又是我们在之前非常熟悉的纯加法运算了。
这样一来,很容易回答之前的问题——为什么要这样变换?——就是为了能够把减法凑成取补和溢出抛弃这两种门电路运算,这样就能让电路能实现减法运算了。
回头再想一想大一上学期刚刚学习过的补码:正数不变,负数绝对值取反后加1,不正是两个括号里的运算吗?
然后,负数运算器便可以顺利成章的画出来:
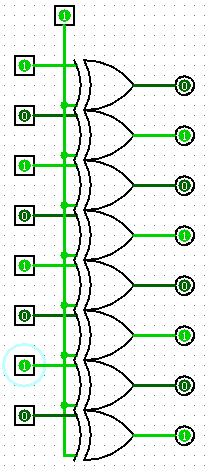
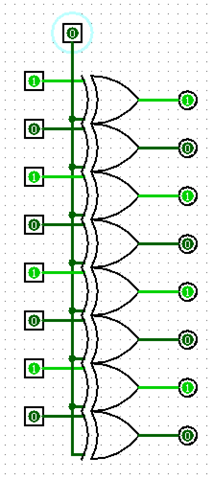
首先,我们要制作一个取反器:
最上方的输入是决定是否取反,如左图,让取反位为1的时候,对数据取反,左边的数据输入为0101 0101,输出为1010 1010.当取反位为0,则不取反,左右相同。本电路仅仅使用了‘抑或’门,它的电路图在之前的加法器中已经做过介绍。
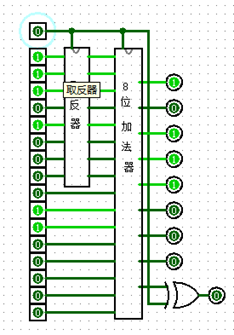
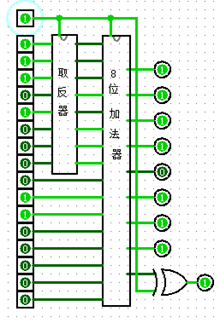
紧接着,我们要把之前做好的8位加法器和这个取反器相连:
这里需要说明的是,两个元件的电路图都可以在这一篇和上一篇文章中得到。红色框所圈的输入位代表应该运行加法还是减法,当运行加法,位值为0,当是减法,位值为1.很显然,当是减法的时候,输入1,取反器对蓝框输入的数字进行取反,8位加法器对粉色框的被减数和蓝色框的减数的逆进行相加,得出的值就是相减的结果。当是加法,红色框位值为0,则取反器不取反,加法器将两数相加。
但是一定会有人有这样的问题:取反后的加一哪去了?我保证仔细读下去5分钟内你就会明白——这是这个设计的最精妙之处。
这里还有两处非常精妙的地方:黑框和8位加法器上方的输入。这里给出解释:
1.上下溢出问题:我们应该都思考过这2个问题——如果两个加数相加和超过了8为存储的范围该怎么办?两数相减如果减出负数怎么办?这两个问题分别成为上溢和下溢。为了解决这个问题,可以设计出黑框里的输出位——第9输出位,当是减法并且下溢的时候,它会输出1,这一点不难分析得知。当是加法并且发生上溢,他也会输出1.这样一来,完美的解决了这个问题。
2.进位问题:还记得之前我们如何制作8位加法器的吗?我们把8个单位加法器相连。但是我们把最低位的那个单位加法器的进位输入位给接地了——也就是默认为二进制的‘个位’没有接收到进位。但是当我们要实现减法的时候,就不是这么轻松了——还记得之前那个算式吗?对减数取反后要加上一。如何实现呢?因为如果是减法,红框将会输入1,那么何不把这个‘1’加到取反之后的那个减数上呢?bingo!就这么办,直接把这个1当成个位的进位就好了~比如说23+45本来等于68,给他的个位进上一位就是69,自然就是+1的效果啦~
好啦,所有原理都解释清楚了,那就试一试吧!
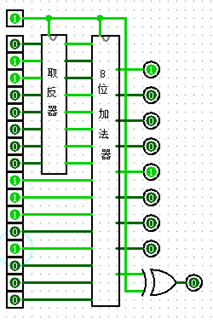
算一算图灵的生日吧~他是6月23日出生,那么我们分别计算6+23,6-23,23-6是多少。
首先6,23的二进制分别是0000 0110和0001 0111.,下面三幅图分别是上面三个运算:
口算一下,答案完全正确!分别是29(0001 1101),-17(m1110 1111),17(0001 0001).
需要注意的是:第二个-17正是-17的补码——17的反码加1.
再看看第三个结果17,对比一下-17和17的二进制码,再想想补码的定义,你一定能感到非常奇妙和有趣!
最后的最后我们再来看看开始的那个问题:
253 – 176 = 253 + ((255 - 176)+ 1) – 256 = ?
用我们的运算器来做一下!
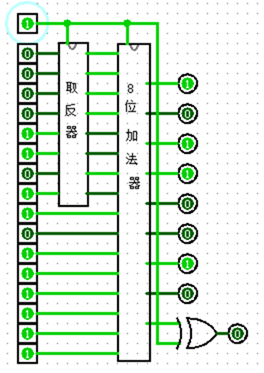 运算器给出的结果是0100 1101,也就是77的二进制,口算一下。。恩。。。完全正确!
运算器给出的结果是0100 1101,也就是77的二进制,口算一下。。恩。。。完全正确!
至此,我们已经做出了一个比较完善的运算器。
但是人类永远不会满足——我怎么样才能把计算的数据和结果一直存到电脑里,这样我就可以不担心我能忘掉他们了。
为了解决这个问题,我们设计的电脑必须具有存储器。它的解决方案就在:http://www.cnblogs.com/sciencefans/p/3188284.html





 浙公网安备 33010602011771号
浙公网安备 33010602011771号