cf800div2A-C题解

一.A

　(1)题意：给你一个数组，让你求最小的（0-1）的距离和。

(2)题解：采用贪心策略，我们肯定是01交题放法，故代码很容易写出来。

(3)代码：

 1 // Problem: A. Creep
 2 // Contest: Codeforces - Codeforces Round #800 (Div. 2)
 3 // URL: https://codeforces.com/contest/1694/problem/A
 4 // Memory Limit: 256 MB
 5 // Time Limit: 1000 ms
 6 // 
 7 // Powered by CP Editor (https://cpeditor.org)
 8 
 9 #include <iostream>
10 #include <queue>
11 #include <vector>
12 #include <cstring>
13 #include <string>
14 #include <map>
15 #include <cmath>
16 #include <algorithm>
17 #include <set>
18 #include <stack>
19 #include <cstdio>
20 #include <climits>
21 #define PII pair<int,int>
22 #define rep(i,z,n) for(int i = z;i <= n; i++)
23 #define per(i,n,z) for(int i = n;i >= z; i--)
24 #define ll long long
25 #define db double
26 #define vi vector<int>
27 #define debug(x) cerr << "!!!" << x << endl;
28 using namespace std;
29 inline ll rd()
30 {
31     ll s,r;
32     r = 1;
33     s = 0;
34     char ch = getchar();
35     while(ch < '0' || ch > '9'){
36         if(ch == '-')
37             r = -1;
38         ch = getchar();
39     }
40     while(ch >= '0' && ch <= '9'){
41         s = (s << 1) + (s << 3) + (ch ^ 48);
42         ch = getchar();
43     }
44     return s * r;
45 }
46 inline void wt(ll x)
47 {
48     if(x < 0) putchar('-'),x = -x;
49     if(x > 9) wt(x / 10);
50     putchar(x % 10 + '0');
51 }
52 ll gcd(ll a,ll b)
53 {
54     if(!b) return a;
55     else return gcd(b,a%b);
56 }
57 ll lcm(ll a,ll b)
58 {
59     return a*b/gcd(a,b);
60 }
61 void solve()
62 {
63     int ze,on;
64     cin>>ze>>on;
65     while(ze&&on){
66         cout<<1<<0;
67         on--;
68         ze--;
69     }
70     while(ze){
71         cout<<0;
72         ze--;
73     }
74     while(on){
75         cout<<1;
76         on--;
77     }
78     cout<<endl;
79 }
80 int main()
81 {
82     int t;
83     t = rd();
84     while(t--){
85         solve();
86     }
87     return 0;
88 }

二.B

　　(1)题意：给你一个01串，你能执行两个操作，第一个操作，能把01变成1；第二个操作，能把10变成0，问你这个字符串存在多少个字串能经过0次或者n次变成长度为1的串。（注意l<=r）

　　(2)题解：我们首先考虑一个字符串最多会有多少个解。

　　　　　　比如说这个01串（长度为8）

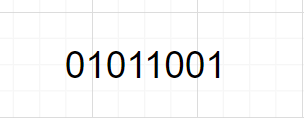
　　　　对于第一个0，会有一个子串0，就是它自己

　　　　对于第二个1，会有三个子串0，1，01，除掉重复的，会有两个

　　　　。。。。。。

　　　　对于第八个1，会有8个子串（不含重复）分别是1，01，001，1001，11001，011001，1011001，01011001

　　　　利用高中学过的等差数列求和公式可知，子串的个数相加就是n*(n+1)/2

　　　我们确定了总共可能的答案数，那么我们去减去不可能构成的串，那么就能构成最后的答案了。而对于每一个不能构成长度为1的串，他的后面两个字母会相同，这样子就会永远变不成1。因此代码可以写出来了

　　(3)代码：

 1 // Problem: B. Paranoid String
 2 // Contest: Codeforces - Codeforces Round #800 (Div. 2)
 3 // URL: https://codeforces.com/contest/1694/problem/B
 4 // Memory Limit: 256 MB
 5 // Time Limit: 1000 ms
 6 // 
 7 // Powered by CP Editor (https://cpeditor.org)
 8 
 9 #include <iostream>
10 #include <queue>
11 #include <vector>
12 #include <cstring>
13 #include <string>
14 #include <map>
15 #include <cmath>
16 #include <algorithm>
17 #include <set>
18 #include <stack>
19 #include <cstdio>
20 #include <climits>
21 #define PII pair<int,int>
22 #define rep(i,z,n) for(int i = z;i <= n; i++)
23 #define per(i,n,z) for(int i = n;i >= z; i--)
24 #define ll long long
25 #define db double
26 #define vi vector<int>
27 #define debug(x) cerr << "!!!" << x << endl;
28 using namespace std;
29 inline ll rd()
30 {
31     ll s,r;
32     r = 1;
33     s = 0;
34     char ch = getchar();
35     while(ch < '0' || ch > '9'){
36         if(ch == '-')
37             r = -1;
38         ch = getchar();
39     }
40     while(ch >= '0' && ch <= '9'){
41         s = (s << 1) + (s << 3) + (ch ^ 48);
42         ch = getchar();
43     }
44     return s * r;
45 }
46 inline void wt(ll x)
47 {
48     if(x < 0) putchar('-'),x = -x;
49     if(x > 9) wt(x / 10);
50     putchar(x % 10 + '0');
51 }
52 ll gcd(ll a,ll b)
53 {
54     if(!b) return a;
55     else return gcd(b,a%b);
56 }
57 ll lcm(ll a,ll b)
58 {
59     return a*b/gcd(a,b);
60 }
61 char a[200010];
62 void solve()
63 {
64     int n;
65     scanf("%d%s",&n,a+1);
66     if(n==1){
67         printf("%d\n",1);
68         return ;
69     }
70     ll ans=1LL*(n)*(n+1)/2;
71     for(int i=1;i<=n;i++){
72         if(a[i]==a[i-1]) ans-=i-1;
73     }
74     cout<<ans<<endl;
75 }
76 int main()
77 {
78     int t;
79     scanf("%d",&t);
80     while(t--){
81         solve();
82     }
83     return 0;
84 }

三.C

　　1.题意：给你一个序列，让你用n个0还原这个序列，你可以做两个操作。第一个：前面那个数加1，指针向后移动一格；第二个：后面那个数减1，指针往前移动一格。（注意，指针初始在第一个位置上，最后一定也要在第一个位置上）

　　2.题解：对于这个题目，我刚开始的思路是正着做，后面发现正着做的时候会有很多麻烦，因此我们考虑把原序列还原成n个0。首先对于这个序列，操作都是互逆的（即你加了1，一定会在某个地方损失1，因此最后如果能恢复成n个0，那么肯定原序列的和肯定为0；第二个发现，对于某一个点，前面如果出现了和小于等于0的时候，此时如果这个位置有值的话肯定是不能构成n个0的，为什么呢？因为如果我们前面有构成0，那么；指针肯定要停留在那里，如果此时你还需要往下，那么原先的指针上的那个数则会+1，导致序列构成错误。（提醒，一定要判小于等于0，样例中给了这个特判）

　　3.代码：

 1 // Problem: C. Directional Increase
 2 // Contest: Codeforces - Codeforces Round #800 (Div. 2)
 3 // URL: https://codeforces.com/contest/1694/problem/C
 4 // Memory Limit: 256 MB
 5 // Time Limit: 1000 ms
 6 // 
 7 // Powered by CP Editor (https://cpeditor.org)
 8 
 9 #include <iostream>
10 #include <queue>
11 #include <vector>
12 #include <cstring>
13 #include <string>
14 #include <map>
15 #include <cmath>
16 #include <algorithm>
17 #include <set>
18 #include <stack>
19 #include <cstdio>
20 #include <climits>
21 #define PII pair<int,int>
22 #define rep(i,z,n) for(int i = z;i <= n; i++)
23 #define per(i,n,z) for(int i = n;i >= z; i--)
24 #define ll long long
25 #define db double
26 #define vi vector<int>
27 #define debug(x) cerr << "!!!" << x << endl;
28 using namespace std;
29 inline ll rd()
30 {
31     ll s,r;
32     r = 1;
33     s = 0;
34     char ch = getchar();
35     while(ch < '0' || ch > '9'){
36         if(ch == '-')
37             r = -1;
38         ch = getchar();
39     }
40     while(ch >= '0' && ch <= '9'){
41         s = (s << 1) + (s << 3) + (ch ^ 48);
42         ch = getchar();
43     }
44     return s * r;
45 }
46 inline void wt(ll x)
47 {
48     if(x < 0) putchar('-'),x = -x;
49     if(x > 9) wt(x / 10);
50     putchar(x % 10 + '0');
51 }
52 ll gcd(ll a,ll b)
53 {
54     if(!b) return a;
55     else return gcd(b,a%b);
56 }
57 ll lcm(ll a,ll b)
58 {
59     return a*b/gcd(a,b);
60 }
61 ll a[200010],pre[200010];
62 void solve()
63 {
64     int n;
65     n=rd();
66     for(int i=1;i<=n;i++) a[i]=rd(),pre[i]=pre[i-1]+a[i];
67     bool neg=false;
68     for(int i=1;i<=n;i++){
69         if(neg&&a[i]){
70             cout<<"No"<<endl;
71             return ;
72         }
73         if(pre[i]<=0) neg=true;
74     }
75     if(pre[n]==0) cout<<"Yes"<<endl;
76     else cout<<"No"<<endl;
77 }
78 int main()
79 {
80     int t;
81     t = rd();
82     while(t--){
83         solve();
84     }
85     return 0;
86 }

posted @ 2022-06-17 19:08 scannerkk 阅读(58) 评论(0) 收藏举报

刷新页面返回顶部

scannerkk

cf800div2A-C题解

公告