P2835修复光盘

一、题目描述

 

 

 

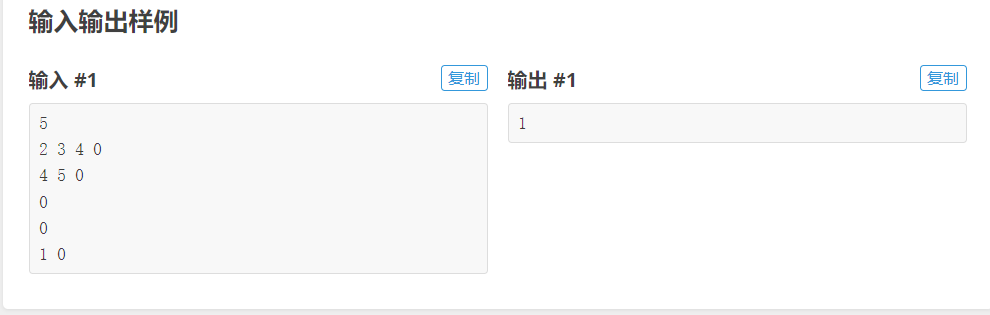
 二、题目分析

　　这个题目挺有意思的，刚开始以为是个并查集的模板题，后面交上去只有36分，仔仔细细看了一下题，发现这并不是双向关系，而并查集是双向的。因此我就想了一个有疑问的想法，在合并祖先的时候，把那些祖先不等于自己的标记一下，最后计算祖先等于自己的或者未被标记的加上去就行了，虽然是100分，但是被hack了一个点。没办法只好向图论进军了，看到n的范围不是很大，果断用floyd，最后ac了。

三、代码实现

　　ACfloyd

 1 #include "bits/stdc++.h"
 2 using namespace std;
 3 int graph[210][210];
 4 int bset[210];
 5 int main()
 6 {
 7     int n,y;
 8     int f = 0;
 9     cin >> n;
10     for(int i = 1;i <= n;i++)
11         bset[i] = i;
12     while(++f <= n)
13         while(cin >> y && y != 0)
14             graph[f][y] = 1;
15     for(int i = 1;i <= n;i++)
16         for(int j = 1;j <= n;j++)
17             for(int k = 1;k <= n;k++)
18                     if(graph[j][k] || (graph[j][i] && graph[i][k]))
19                     graph[j][k] = 1;
20     for(int i = 1;i <= n;i++)
21         for(int j = 1;j <= n;j++)
22             if(graph[i][j])
23                 bset[j] = bset[i];
24     int cnt = 0;
25     for(int i = 1;i <= n;i++)
26         if(i == bset[i])
27             cnt++;
28     cout << cnt;
29     return  0;
30 }

　　假AC并查集

 1 #include "bits/stdc++.h"
 2 using namespace std;
 3 int a[210],vis[210];
 4 void init()
 5 {
 6     for(int i = 1;i <= 200;i++)
 7         a[i] = i;
 8 }
 9 int find(int u)
10 {
11     return  (a[u] = u == a[u]?u : find(a[u]));
12 }
13 int main()
14 {
15     init();
16     int n,y;
17     cin >> n;
18     int f = 1;
19     while(f <= n){
20         while(cin >> y && y != 0){
21             int t1,t2;
22             if(y != f)
23                 vis[y] = 1;
24             t1 = find(f);
25             t2 = find(y);
26             a[t2] = t1;
27         }
28         f++;
29     }
30     int cnt = 0;
31     for(int i = 1;i <= n;i++)
32         if(i == a[i] || !vis[i])
33             cnt++;
34     cout << cnt;
35     return 0;
36 }
posted @ 2022-01-20 20:30  scannerkk  阅读(41)  评论(0)    收藏  举报