【数据结构】排序2 插入排序

插入排序的基本思想：
每次将一个待排序的记录按其关键字大小插入前面已经排好序的序列，直到全部关键字都插入到子序列中为止。
根据这种思想有这几种常用的插入排序算法：直接插入，折半插入和希尔排序。

1.直接插入排序

这是最直接的一种插入排序算法，排序表在排序过程中会分为三部分：排好序的有序序列L[1…i-1]、当前处理元素L(i)、剩余的无序序列L[i+1…n]。
初始情况下，有序序列中有第一个元素L(1)，每次从无序序列中取出一个插入到有序序列中去，直到最后无序序列的长度为0，所有元素都已排好序。
算法具体实现：

点击查看代码

void InsertSort (ElemType A[] , int n ) {
	int i,j;
	for (i = 2; i<= n; i++ ) 
	if (A[i] < A[i-1] ){//对于指针i，其前面的序列都是已经排好序的，最大关键字就是A[i-1]
//所以只有当A[i] < A[i-1]时才进行如下的操作
//否则的话就代表位置合适无需移动A[i]
	A[0] = A[i];
	for (j = i-1 ;A[0] < A[j] ; --j)
	A[j+1] = A[j];
//这里循环结束条件为A[j]≤A[0]代表了两种情况
//A[j]代表已排序序列中当前被移动的关键字,A[0]代表当前被排序的元素
//第一种情况是在中途遇到了被排序元素的合适位置，而从j+1到i-1的元素都已经向后移了一位，则把原来的A[i]移到j+1处即可
//第二种情况是走到了头遇到了哨兵A[0]（这里可以看出哨兵机制的边界检测功能），则当前被排序元素是最小的元素，此时j+1就是第一个元素，把原来的A[i]移到j+1处即可
	A[j+1] = A[0];//此时的j+1就是原来的A[i]的正确位置
	}
}

插入排序过程示例：

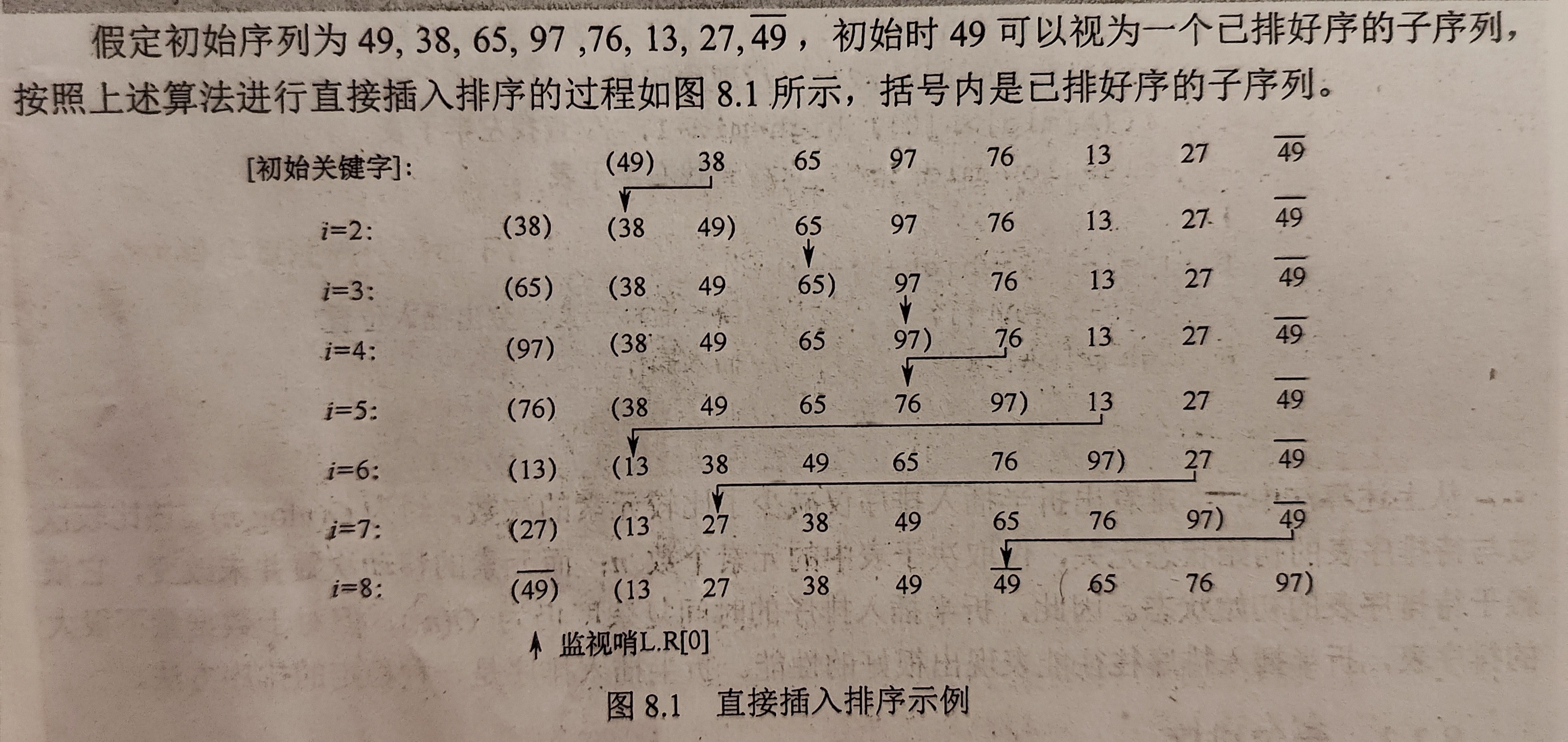
这个例子里也涉及到了两个元素关键字相等的情况。

算法性能分析：

稳定性：
前面说到稳定性是指排序前后序列中两个关键字相同的元素的相对位置不会改变。根据前面对算法过程的分析容易知道，直接插入排序是满足稳定性的。
适用性：
由于这个算法不需要随机存取，所以适用于顺序存储和链式存储的线性表。

2.折半插入排序

折半插入是对直接插入排序的改进。
在直接插入的算法过程中，由于前面的已排序好的序列是有序的所以处理元素时逐个比较并前移找插入位置就显得太繁复。

折半插入的思想：
直接插入的算法过程是在已排序序列中一边比较一边移动元素，而折半查找中把这两个过程分开，先用折半查找直接查找出元素的待插入位置，再统一将待插入位置之后的元素后移一位腾出位置。
由于折半查找是基于随机存取的算法，所以折半插入只能适用于顺序存储结构。

代码解析：



折半插入的算法性能分析：
折半插入只减少了比较元素的次数，而元素的移动次数没有改变。折半查找中比较元素的次数只与元素个数n有关，与序列的初始情况无关。所以当数据量n较小时，折半查找能体现出其优势。
其总体时间复杂度仍为O(n^2)。
折半插入是一种稳定的排序算法，这一点与直接插入排序没有区别。

3.希尔排序

希尔排序是根据直接插入排序算法的性质对其的一种改进。
算法思想概述：
直接插入排序算法的时间复杂度与其序列初始情况和序列长度n有很大的关系，根据这个信息，希尔排序的改进思路就是先把大序列分成小序列分别进行直接插入排序，这样由于减小了序列长度时间复杂度会减小；再对这个经过初步处理的序列进行再次直接插入排序，由于此时序列已经呈现初步的有序性，所以会有利于减小直接插入的时间复杂度。

算法过程：

希尔排序的独特之处在于其分组的策略。相当于某种等距取样，但是每一组的元素个数一般会不一样，只有当序列长度n为所取步长的整倍数时每组的元素个数才会相同。
随着步长的逐渐增大，每组的元素个数会逐渐增多，而组数会逐渐减少，序列的有序性也逐渐增大，这一方面是为了完成最终的排序的目的，一部分又减小下一轮排序的复杂度。
直到最后一次步长为1时，整个序列只分为一组，这时进行的就是对整体的直接插入排序，但由于前面的多轮处理工作，这个排序会非常快。
示例如图：

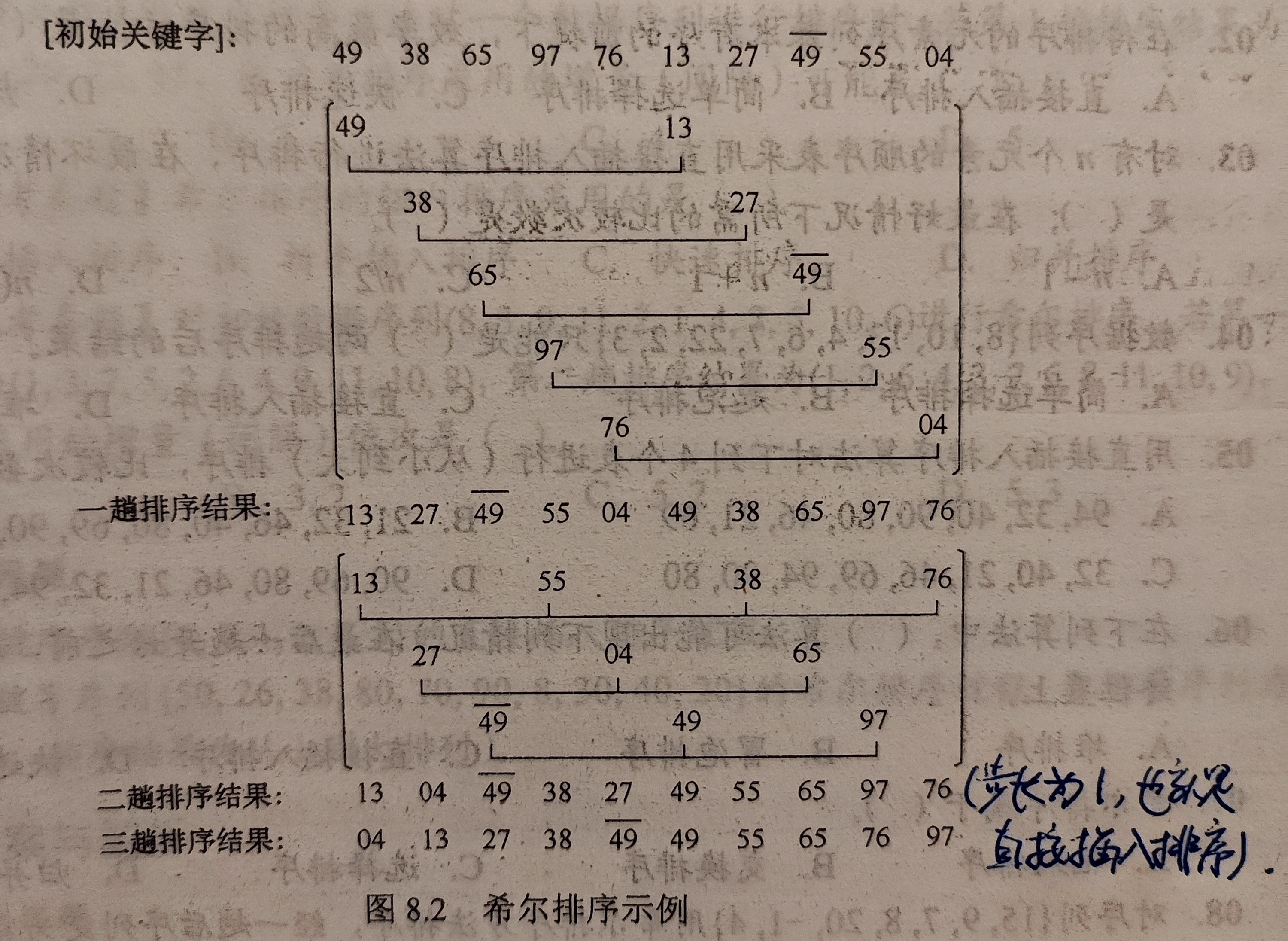
这里取的步长分别为5、3、1。
步长的选取是根据实际情况选取的，并没有很固定的标准。

(这里的步长选取原则是初始时取n/2，每轮排序将步长减半)


算法性能分析：