谨本人学习数据结构算法的经历记录

数据结构

存储方式只有数组（顺序存储）和链表（链式存储）

基本操作就是增删改查，遍历方式 -> (线性)迭代(for,while循环)和(非线性)递归。

1.1 、基本概念

数据

什么是数据？

描述客观事务的数值、字符.....，能输入到计算机并且被计算机处理的各种符号的集合
数据就是信息在计算机中的表示

数据元素

数据元素就是数据的基本单位

在计算机程序中，通常把数据元素作为一个整体进行处理

例：

描述学生信息的一条记录就是一个数据元素

描述一个坐标点的信息就是一个数据元素

数据元素通常由若干的数据项组成

例：

描述学生信息中的姓名、学号、成绩都是数据项

坐标点的横坐标，纵坐标就是数据项

数据对象

一组相同性质的数据元素的集合

例：

学校中所有学生的集合就是数据对象。

平面坐标系中所有点的集合就是数据对象。

数据结构

相互之间存在一种或多种特定关系的数据元素的集合

数据结构就是数据元素之间的关系

数据结构分为逻辑结构和物理结构。

数据的逻辑结果由四种：

集合：数据仅仅属于同一个集合，没有其他相互关系

线性：描述一对一的关系。

树形：描述一对多的关系。

图形：描述多对多的关系。

数据的逻辑结构一般采用二元组的形式定义：

数据结构 = （D，S）

D ：数据元素的集合

S ：D （数据元素的集合）中元素之间的关系的集合

例 1 ：

二元组： set = (D，S)

D = {01，02，03，04，05，06}

S = {}

在 set 集合中，数据元素除了属于同一个集合外，不存在其他的关系。

这就是集合结构 , 数据和数据之前没有关系

例 2 ：

二元组： linearity = (D，S)

D = {01，02，03，04，05，06}

S = {<01,02>, <02,03>, <03,04>, <04,05>, <05,06>}

在数据结构 linearity 中，数据结构是有序的。

有一个被称为 “第一个” 的数据元素（元素01），和一个被称为 “最后一个” 的数据元素（元素06），、

除了第一个元素外，其他每一个元素都有一个直接前驱元素。（即前面都有元素）

除了最后一个元素外，其他每一个元素都有一个直接后继元素。（即后面都有元素）

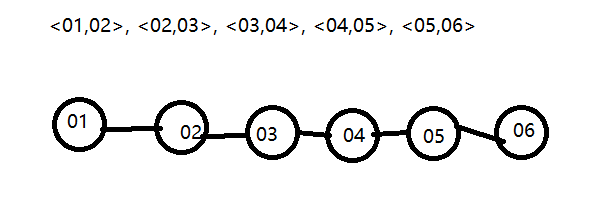
数据元素之间是 1 对 1 的关系，就是线性关系。

例 3 ：

二元组： tree= (D，S)

D = {01，02，03，04，05，06}

S = {<01,02> ,<01,03> ,<02,04> ,<02,05> ,<03,06>}

在 tree 数据结构中，除了第一个元素（元素 01 ）外，每个元素都有并且只有一个直接前去元素，每个元素可以有多个直接后继元素

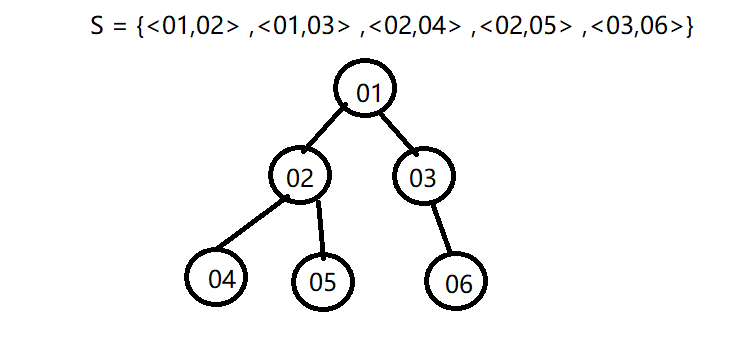
数据元素之间是 1 对多的关系，将之称为树型结构。

例 4 ：

二元组： graph = (D，S)

D = {01，02，03，04，05，06}

S = {<01,02> ,<01,03> ,<02,05> ,<05,06> ,<06,02> ,<05,04> ,<04,05>}

在 graph 数据结构中，每个元素可以有多个直接前驱元素，每个元素也可以有多个直接后继元素。

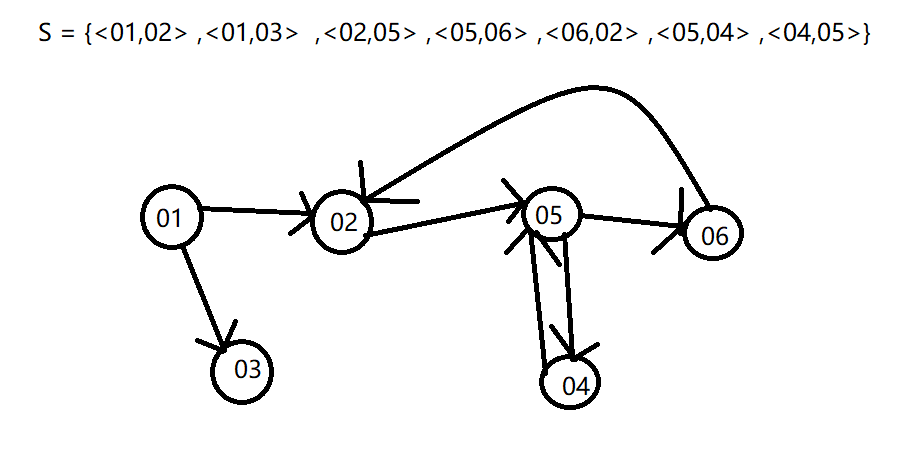
这种数据结构的特点：多对多的关系，将其称为图形结构

小结：

数据的物理结构就是逻辑结构在计算机中的存储表示。它有两种表示形式：

顺序存储，链式存储

1、顺序存储：就是使用一块连续的存储空间，数据之间紧挨在一起。数据的前驱与后继的关系可以通过数据元素在内存种相对位置反应出来。

2、链式存储：数据元素的存储位置不是连续的，每个元素保存下一个元素的存储地址。

2.1、抽象数据类型

数据类型

一组性质相同的数据的集合及该数据集合上操作的总称。

譬如 Java 中 int 类型，数据的集合： -2147483648~2147483647 ，

在这组数据上的操作：加、减、乘、除、求余 .....

抽象数据类型

abstract data type ，简称 ADT

由一组数据模型及该模型上的一组操作组成，

抽象数据类型 ADT ，仅仅讨论它的逻辑特性，不关心实现。

抽象数据类型一般使用一个三元组表示：

ADT = {D，S，P}

D 是数据对象。S 是 D 上的关系。P 是 D 上的操作。

在定义抽象数据类型，可以使用以下的格式：

ADT 抽象数据类型名 {

数据对象：<数据对象的定义>

数据关系：<数据关系的定义>

数据操作：<基本操作的定义>

}

抽象数据类型可以对应一个 Java 类：

数据对象与数据关系可以通过类的成员变量来存储和表示，

数据操作可以使用方法；来实现。

3.1、算法及性能分析

1.3.1 算法

算法就是为解决某一个特定问题而规定的一系列的操作。是一组有序的指定的集合。

数据结构与算法就是一对闺蜜（即两者之间必然有某种直接或间接的联系）

譬如：求一组数字的累加和？

public class JavaArithmeticDemo () {
    public static void main(String[] args) {
        t2(100);
    }
    
    // 四行代码
   public static void t1 (int num) {
        int m = 0;
        for (int i = 1; i <= num ;i++) {
            m += i ;
        }
        System.out.println("累加和为 : " + m);
    }
    
    // 高斯算法
    // sum = 1 + 2 + 3 + 4 + .....+ 100
    // sum = 100 + 99 + 98 + 97 + ...+1
    // 两倍sum = 101 * 100
    // 两行代码 
    public static void t2(int num) {
        int m = num * (num+1) / 2 ;
        System.out.println("累加和为 : " + m);
    }
}

算法有五个特性：

输入：一个算法有 0 个或多个输入；

输出：至少有一个输出；

有穷性：算法中执行指令的个数应该是有限的，执行有穷的步骤后能结束；

确定性：对于特定的合法输入，它的输出应该是唯一的；

可行性：算法能够实现，并且在有限的时间内完成；

算法设计要求

正确性：没有语法错误，对于合法的输入产生满足需求的输出。对于特定的输入也能够产生正确的输出。

可读性：算法另一个目的是为了交流，方便阅读。

健壮性：对于不合理的输入要求，也能给出合理的提示信息，而不是程序崩溃。

时间效率高与存储空间小。

评价一个算法性能的好坏。实际上就是评价算法的资源占有率。计算机最重要的资源就是时间和空间。

使用时间复杂度衡量程序运行需要的时间。

使用空间复杂度衡量程序所占内存的大小。

1.3.2 时间复杂度

讨论计算机程序运行的时间可以采用以下方法：

时候统计

编程实现这个算法，统计所需要的时间。

事前分析

采用渐进时间复杂度分析估算，

渐进时间复杂度，简称时间复杂度，在进行算法分析时，语句总的执行次数，记作 T(n) 。是关于问题规模 n 的函数，分析 T(n) 随着问题规模 n 的变化情况，确定 T(n) 的数量级。

T(n) = O(f(n)) ，表示随着问题规模 n 的增大，算法执行的时间增长率和 f(n) 函数的增长率相同， f(n) 是问题规模 n 的一个函数

随着输入规模 n 的增大，T(n) 增长越慢的算法越好。

1.3.3 算法时间复杂度分析

https://blog.csdn.net/c99463904/article/details/77414163

预估代码的基本操作执行次数。

算法1、：

计算 1+2+3+4+......+n 的累加和，高斯算法

public static void sum01(int n) {
    int sum = n * (n + 1) / 2 ;
}

顺序执行，时间复杂度 T(n) = O(1) ，是常数阶

算法2、：

计算 1+2+3+4+......+n 的累加和

public static void sum02(int n) {
    int sum = 0;
    for (int i = ; i <= n ; i++) {
        sum += i ;
    }
}

T(n) = O(n) ，线性阶【增长率和n的规模有关】

算法3、：

计算 1+2+3+4+......+n 的累加和

public static void method01(int n) {
    int i = 1;
    int count = 0;
    while(i <= n) {
        i = i * 2;
        count++;
    }
}

循环控制变量 i 的值：1，2，4，8，16 ....2的x次方，当执行了 x 次，i 的值为 2的x次方时循环结束。

循环条件 i <= n ，2的x次方 <= n 不成立时循环退出

T(n) = O(logn) n的对数

算法 4、：

public static void method02(int n) {
    int count = 0;
    int s = 0;
    while(s <= n) {
        count++ ;
        s = s + count;
    }
}

假设循环执行 x 次，count 变量在循环过程中的值：0，1，2，3，4，5，。。。。。x

在执行完第 x 次后循环结束，s <= n 不成立时，s的值是

s = 0+1+2+3+....x = x*（x+1）/ 2 = (x二次方 + x ) / 2

T(n) = O(n的二次方);

算法5、：

public static void method(int n) {\
    int count = 0;
    for (int i = 1; i<= n; i++) {
        for (int j = 1; j <= n; j++) {
            count ++;
        }
    }
}

T(n) = O(n的二次方)

常见时间复杂度函数的增长率

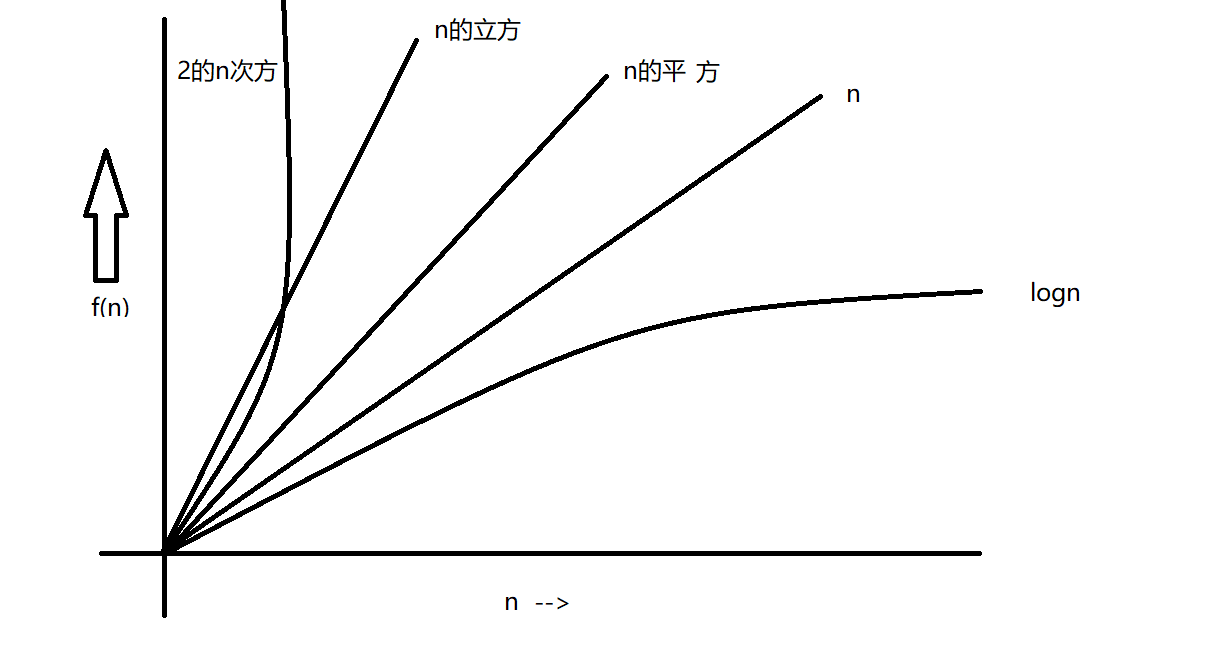
1.3.4 空间复杂度

为了求解某一问题，在执行操作期间所需要的存储空间大小。不包含用来存储输入所需要的空间。

记作：

S(n) = O(f(n))

结论：

算法的空间复杂度是以时间复杂度为上限的。

1 线性表

1.1 线性表的抽象数据类型

数据结构的四种逻辑结构：集合、线性、树状、网状、

linearity = (D,R)

D = {a1,a2,a3,a4}

R = {<a1,a2>,<a2,a3>,<a3,a4>}

a1元素称为第一个元素，其他的元素都有一个直接前驱元素。

a4元素称为最后一个元素，其他的元素都有一个直接后继元素

生活中的线性结构：排队，火车，

1.1 线性表的抽象数据类型

ADT List {

数据对象：D = {ai 属于某个数据对象，i=0，1，2，3，4}

D={a0，a1，a2，a3，a4 ...an}，所有的元素都是同一个数据类型

数据关系：R={<a1,a1+1>}

数据操作：

getSize() ：返回线性表中元素的个数

isEmpty() ：判断线性表是否为空

insert(i,e) ：在线性表中的 i 索引值位置插入 e 元素

contains(e) ：在线性表中判断是否存在元素 e，存在则返回 true

indexOf(e) ：返回元素 e 在线性表中的索引值，不存在则返回 -1

remove(e) ：删除线性表第一个与 e 相同的元素，删除成功则返回删除的元素

remove(i) ：删除线性表中指定索引值的元素，返回删除的元素

replace(i,e) ：把线性表中索引值为 i 的元素替换为元素e ，返回旧的元素

get(i) ：返回线性表中索引值为 i 的元素

insertBefore(p,e) ：在线性表中元素 p 的前面插入元素e

insertAfter(p,e) ：在线性表中元素 p 的后面插入元素e

涉及到索引值的地方，都要设置索引越界，则报错

}

1.2 List接口

使用 Java 中的接口来表示 ADT 中的数据操作，在使用类完成抽象数据类型时，只要这个类实现接口即可完成抽象数据类型中定义的操作。

package com.yuanwu.ei;

public interface MyList {
	int getSize();		// 返回线性表中元素的个数
	boolean isEmpty();	//判断是否为空
	void insert(int i ,Object e);	// 在线性表中的 i 索引值位置 插入 e 元素 
	boolean contains(Object e);		// 在线性表中判断是否存在元素 e，存在则返回 true 
	int indexOf(Object e);			// 返回元素 e 在线性表中的索引值 ，不存在则返回 -1
	Object remove(Object e);		// 删除线性表第一个与 e 相同的元素 ，删除成功则返回删除的元素
	Object remove(int i);			// 删除线性表中指定索引值的元素 ，返回删除的元素
	void replace(int i ,Object e);	// 把线性表中索引值 为 i 的元素替换为 元素e ,返回旧的元素
	Object get(int i);				// 返回线性表中索引值为 i 的元素
	boolean insertBefore(Object pObject ,Object e);	// 在线性表中元素 p 的前面插入元素e 
	boolean insertAfter(Object pObject ,Object e);		// 在线性表中元素 p 的后面插入元素e
}

1.3 线性表的顺序存储与实现

1.3.1 插入元素

insert(int i ,Object e) ,i 索引，e 元素

1）、需要时，可以对数组扩容

2）、把 i 位置开始的元素依次后移

3）、把要插入的元素保存到 i 位置

1.3.2 删除元素

remove(int i)

1）、从 i+1 开始，把元素依次前移，

2）、把最后一个元素置为 null

1.3.3 具体代码的实现

/**
 * 通过数组实现线性表 
 * */
public class MyArrayList implements MyList {
	private Object[] elements;	//定义数组保存数据元素 
	private static final int DEFAULT_CAPACITY = 16;	//定义数组的初始长度（容量）
	private int size;
	
	// 构造方法 
	public MyArrayList() {
		elements = new Object[DEFAULT_CAPACITY];
	}
	public MyArrayList(int initialCapacity) {
		elements = new Object[initialCapacity];
	}
	
	// 返回元素的个数
	@Override
	public int getSize() {
		return size;
	}

	@Override
	public boolean isEmpty() {
		// 判断线性表是否为空
		return size == 0;
	}

	@Override
	public void insert(int i, Object e) {
		// 在线性表的 i 位置 插入 元素 e
		// 判断 索引值 i 是否越界
		if (i <0 || i > size) {
			throw new IndexOutOfBoundsException(i + "越界");
		}
		// 如果数组容量满了，对数组扩容
		if (size >= elements.length) {
			expandSpace();		// 数组扩容 
		}
		// 从 i 开始 ，把元素依次后移	
		for (int j = size; j > i; j--) {
			//  把 elements[j-1] 的值 赋值给 elements[j]
			//	数组长度-1的数据 赋值给 当前 数组索引，实现 元素后移 
			elements[j] = elements[j-1];
		}
		// 把元素e 存储到 i 位置
		elements[i] = e;
		// 元素个数 +1
		size++;
	}
	
	private void expandSpace() {
		// 定义一个更大的数组 ,默认2倍扩容数组 
		Object[] newElements = new Object[elements.length * 2];
		// 让原来数据的内容复制到新的数组中
		for (int i = 0; i<elements.length; i++) {
			newElements[i] = elements[i];
		}
		// 让原来的数组指向新的数组
		elements = newElements ;
	}
	
	// 判断当前线性表中是否包含元素 e
	@Override
	public boolean contains(Object e) {
		return indexOf(e) >= 0;
	}

	// 返回元素e 在线性表中i第一次出现的索引值 ，不存在则返回 -1
	@Override
	public int indexOf(Object e) {
		if (e != null) {
			for (int i = 0; i < size; i++) {
				if (e.equals(elements[i])) {
					return i;
				}
			}
		}
		return -1;
	}
	
	// 删除 指定元素的 元素 
	@Override
	public Object remove(Object e) {
		// 返回元素e 第一次的出现的索引值 ，
		int index = indexOf(e);
		if (index < 0) {
			throw new IndexOutOfBoundsException("数组下标越界");
		}
		return remove(index);
	}

	// 删除指定的索引值发元素 
	@Override
	public Object remove(int i) {
		// 判断 i 是否越界 
		if (i < 0 || i > size) {
			throw new IndexOutOfBoundsException("数组下标越界");
		}
		// 保存删除的元素
		Object old = elements[i];
		// 把 i+1 开始的元素依次前移 。
		for (int m = 0; m < size - 1; m++) {
			elements[m] = elements[m+1];
		}
		// 把最后的元素位置置为null
		elements[size - 1] = null;
		// 修改元素的个数
		size--;
		return old;
	}

	// 把线性表中索引值 为 i 的元素替换为 元素e ,返回旧的元素
	@Override
	public Object replace(int i, Object e) {
		// 判断索引值示符越界 
		if (i < 0 || i > size ) {
			throw new IndexOutOfBoundsException("数组下标越界");
		}
		// 保存被替换的元素
		Object old = elements[i];
		// 替换 
		elements[i] = e ;
		// 把原来的元素返回
		return old;
	}

	// 返回指定位置的元素
	@Override
	public Object get(int i) {
		if (isIndexBounds(i)) {
			return elements[i];
		}
		return null;
	}
	
	// 判断索引值是否越界
	public boolean isIndexBounds(int i) {
		if (i < 0 || i > size) {
			throw new IndexOutOfBoundsException("数组下标越界");
		}
		return true;
	}

	// 在指定的元素前插入一个元素
	@Override
	public boolean insertBefore(Object pObject, Object e) {
		// 确定元素 p 在线性表中的位置
		int index = indexOf(pObject);
		if (index < 0) {
			return false;
		}
		insert(index, e);
		return true;
	}

	// 在指定的元素 后插入一个元素
	@Override
	public boolean insertAfter(Object pObject, Object e) {
		// 确定元素 p 在 线性表中的位置
		int index = indexOf(pObject);
		if (index < 0) {
			return false;
		}
		insert(index + 1, e);
		return true;
	}
	
	@Override
	public String toString() {
		StringBuffer sBuffer = new StringBuffer();
		sBuffer.append("[");
		for (int i = 0; i < size; i++) {
			sBuffer.append(elements[i]);
			if (i < size - 1) {
				sBuffer.append(",");
			}
		}
		sBuffer.append("]");
		return sBuffer.toString();
	}

}

1.3.4 顺序存储的特点

优点：

顺序存储时使用数组实现的，数组可以通过索引值快速访问每个元素

int [] data = new int[4];

data -> 数组名实际上是变量名，存储在栈区指向堆的存储地址指向 [ 地址 0x1234 ]

new 关键字会在堆分配一块存储空间。 [ 地址 0x1234 ]

data[2] = 666;

为什么通过下标就可以访问数组元素？

通过下标可以计算数组元素的地址：

data[2] 元素的地址计算公式：

data + 2 * 4

data 是数组名，保存数组的起始地址

2 是下标

4 是数组元素类型所占的字节数，数组中存储的是 int 类型，每个元素占 4个字节

0x1234 + 2 + 4

缺点：

在插入 / 删除时，需要移动元素，

而且线性表长度是固定的，很难确定存储容量

应用场景：

适合查询操作，

1.4 线性表的链式存储与实现

1.4.1单向链表

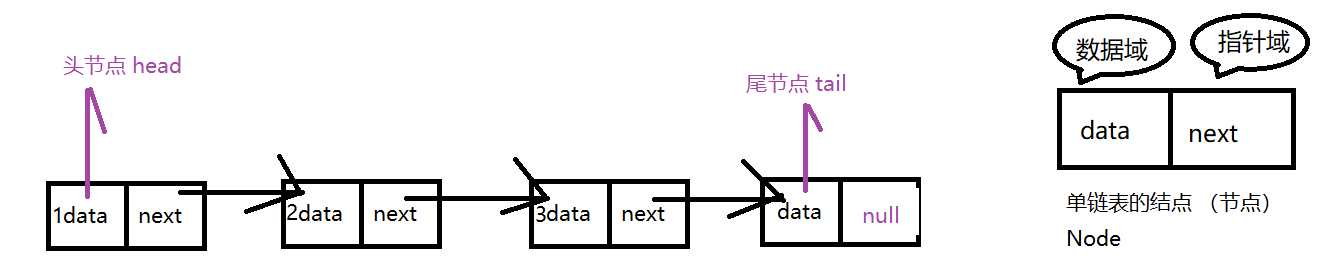
单向链表，也称为单链表，每个存储单元至少有两个存储域，一个用来存储数据，另一个保存下一个存储单元的引用。

各个存储单元的地址可以是不连续的。【一个数据域和一个指针域组成的就是一个存储单元】称为节点 Node

单链表插入 / 删除分析

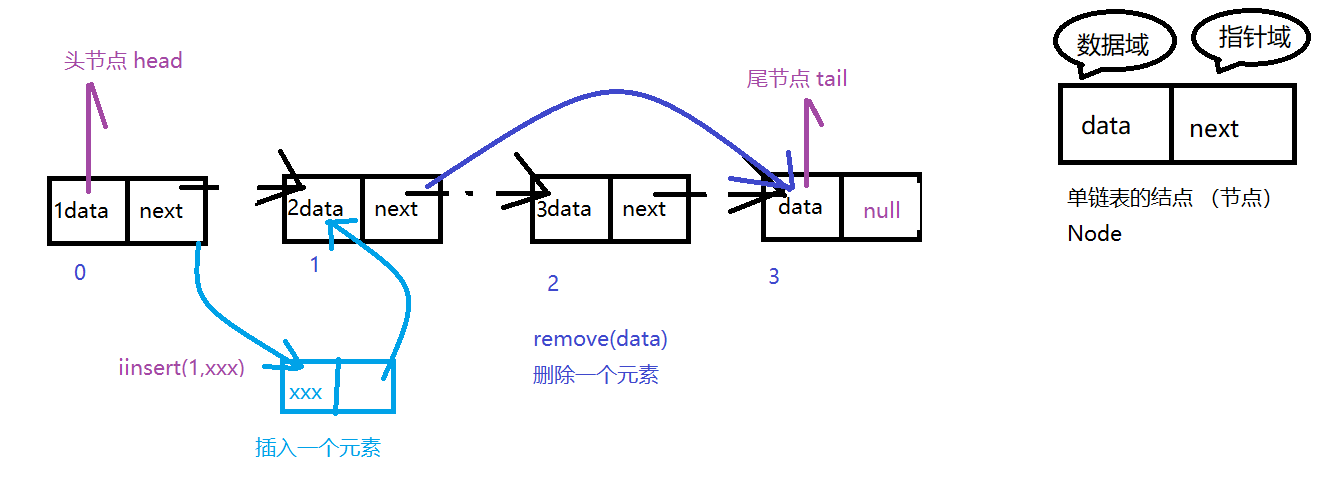
1.4.2 通过单向链表实现线性表

插入难点 。*** 节点指向，引用指向。

// 在线性表中插入元素
Node pNode = head;
for (int x = 1; x < i; x++) {
pNode = pNode.next; // 循环8次，指向的是第8个节点
}
// 1、修改刚插入的节点的 next域指向
/*

假设循环9次 pNode = head【头节点】

第一次 pNode.next 【指向第一个节点】

第二次 pNdex.next.next

------------------------------------------------------>>>>

pNode.next 指向的是第8次的下一个节点引用

newNode.next = pNode.next

新节点的下一个节点的引用指向 pNode.next 指向的是第九次的节点引用
* 新节点的下一个节点引用指向第八个节点的下一个节点引用【8的下一个节点引用是 9，新节点的下一个节点引用指向9】

pNode.next = newNode

第8个节点的下一个节点引用指向新节点

*/
// 先修改新节点的next指针域，再修改i-1 这个节点的next指针域
newNode.next = pNode.next; // 新插入的节点的下一个节点引用指向 pNode的下一个节点引用
pNode.next = newNode; // 第8个节点的下一个节点引用指向新节点
}
}
// 元素个数 +1
size++;
}

实现接口

package com.yuanwu.ei.dao.Impl;

import com.yuanwu.ei.dao.MyList;

/**
 * 通过单向链表 实现 线性表 
 * */
public class MySingleLink implements MyList{
	private Node head;	// 头节点
	private int size;	//保存元素的个数
	
	// 返回元素个数
	@Override
	public int getSize() {
		return size;
	}

	// 判断 是否为空 
	@Override
	public boolean isEmpty() {
		return size == 0;
	}

	// 在线性表中插入元素
	@Override
	public void insert(int i, Object e) {
		// 判断索引是否越界
		if (i < 0 || i > size) {
			throw new IndexOutOfBoundsException("线性表下标越界");
		}
		// 创建节点 
		Node newNode = new Node(e, null);
		// 头节点 为 null 的情况 ,链表不存在，刚刚添加的节点 就是头节点 。
		if (head == null) {
			head = newNode;
		} else {
		// 在 0 位置插入节点 
			if (i == 0) {
				// 新节点的 next域(指针域) 指向原来的头节点 
				newNode.next = head;
				// 插入的节点 就是新的头节点
				head = newNode ;
			} else {
				// 插入节点  ,先找到 i-1 的节点 ，前一个节点 ，后一个节点 。
				// 假设 i=9 x
				Node pNode = head;
				for (int x = 1; x < i; x++) {
					pNode = pNode.next;	// 循环8次 ，指向的是  第8个节点
				}
				// 1、修改 刚插入的节点的 next域 指向 
				/*
				 * 假设 循环9次	pNode = head【头节点】 
				 * 第一次 pNode.next		【指向第一个节点】
				 * 第二次 pNdex.next.next
				 * 第三次 pNode.next.next.next 
				 * 假设 newNode  节点 <a,0x112>	8前一个节点 <c,0x111> <-9-> 后一个节点是  10<b,0x113>
				 * 因为 pNode = pNode.next pNode 实际上是 pNode.next ，现在又来一个 next域 
				 * 如果pNode.next 指向的是  第八次循环的 pNode   即指向 <c,0x111>
				 * ------------------------------------------------------>>>>
				 * pNode.next	指向的是 第九次的 节点引用 
				 * newNode.next = pNode.next
				 * 新节点的 下一个节点的引用 指向                pNode.next	 指向的是 第九次的 节点引用 
				 * 新节点的下一个节点引用 指向 第八个节点的下一个节点引用 【8的下一个节点引用是 9，新节点的下一个节点引用指向9】
				 * pNode.next = newNode
				 * 第8个节点的下一个节点引用 指向 新节点 
				 * */
				// 先修改 新节点的next指针域 ，再修改i-1 这个节点的next指针域 
				newNode.next = pNode.next;	// 新插入的节点的下一个节点引用 指向 pNode的下一个节点引用
				pNode.next = newNode;		// 第8个节点的下一个节点引用 指向 新节点 
			}
		}
		// 元素 个数 +1
		size++;
	}

	// 判断线性表中是否包含指定的元素 
	@Override
	public boolean contains(Object e) {
		return indexOf(e) >= 0;
	}

	// 返回 元素e 在线性表中第一次出现的 索引值
	@Override
	public int indexOf(Object e) {
		int i = 0;
		Node pNode = head;
		while (pNode != null) {
			// 如果 e==null 并且 节点的数据域 == null ，返回0
			if (e == null && pNode.data == null) {
				return i;
			} else if (e != null && e.equals(pNode.data)) {
				return i;
			}
			i++;
			pNode = pNode.next;
		}
		return -1;
	}

	// 从线性表中 删除 第一个与e相同的元素
	@Override
	public Object remove(Object e) {
		// 找到元素e 第一次出现的索引值
		int index = indexOf(e);
		if (index < 0) {
			return null; //元素不存在
		}
		return remove(index);
	}

	// 从线性表中删除指定索引值的元素
	@Override
	public Object remove(int i) {
		if (i < 0 || i >= size) {
			throw new IndexOutOfBoundsException("线性表下标越界");
		}
		Node pNode = head;
		// 删除头节点 
		if (i == 0) {
			head = head.next;
			size--;
			// 返回删除头节点的数据
			return pNode.data;
		}
		// 找到 i-1这个节点
		for (int x = 1; x < i; x++) {
			pNode = pNode.next;
		}
		// 保存删除节点的数据
		Object old = pNode.next.data;
		// 修改 i-1 next域的指向 i+1 节点 【指向当前节点的下一个节点引用，再下一个节点的引用的节点】
		pNode.next = pNode.next.next;
		size--;
		return old;
	}

	// 把线性表中索引值 为 i 的元素替换为 元素e ,返回旧的元素
	@Override
	public Object replace(int i, Object e) {
		// 判断是否越界
		checkIndexBounds(i); 
		// 找到 索引值为 i 的元素 
		Node pNode = getNode(i);
		// 保存原来的数据
		Object old = pNode.data;
		// 替换
		pNode.data = e;
		return old;
	}

	// 返回线性表中 i 索引值的位置
	@Override
	public Object get(int i) {
		checkIndexBounds(i);
		Node pNode = getNode(i); 
		return pNode.data;
	}

	// 在指定元素 pObject 的前面插入 元素 e
	@Override
	public boolean insertBefore(Object pObject, Object e) {
		// 找 pObject 的位置
		int index = indexOf(pObject);
		if (index < 0) {
			return false;	//元素不存在
		}
		insert(index, e);
		return true;
	}

	// 在指定元素 pObject 的后面插入 元素 e
	@Override
	public boolean insertAfter(Object pObject, Object e) {
		// 找 pObject 的位置
		int index = indexOf(pObject);
		if (index < 0) {
			return false;	// 元素并不存在
		}
		insert(index + 1, e);
		return true;
	}
	
	// 定义一个内部类表示单向链表中的节点 。
	private class Node{
		Object data;	// 保存数据
		Node next;		// 下个节点的引用 
		public Node(Object data ,Node next) {
			this.data = data;
			this.next = next;
		}
	}
	
	// 检查索引值是否越界
	private void checkIndexBounds(int i) {
		if (i < 0 || i >=size) {
			throw new IndexOutOfBoundsException("线性表下标越界");
		}
	}
	
	// 定义一个方法 ，返回 i 索引值的元素
	private Node getNode(int i ) {
		if (i < 0 || i >= size) {
			return null;
		}
		if (i == 0) {
			return head;
		}
		// 找到 i 节点 
		Node pNode = head;
		for (int x = 1; x <= i; x++) {
			pNode = pNode.next;
		}
		return pNode; 
	}

	// 重写 toString
	@Override
	public String toString() {
		StringBuilder sBuilder = new StringBuilder();
		sBuilder.append("[");
		Node pNode = head;
		while(pNode != null) {
			sBuilder.append(pNode.data);
			if (pNode.next != null) {
				sBuilder.append(",");
			}
			pNode = pNode.next;	// 指针下移
		}
		sBuilder.append("]");
		return sBuilder.toString();
	}
}

1.4.3 双向链表

单向链表只能通过一个节点的引用访问他的后继节点，不饿能访问前驱节点，如果要找某个节点的前驱节点，需要从头结点开始依次查找。

在双向链表中，扩展了节点的结构，每个节点除了存储数据外，通过一个引用指向后继节点，再定义一个引用指向前驱节点：

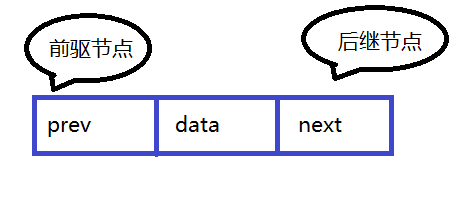
双向链表的结构：

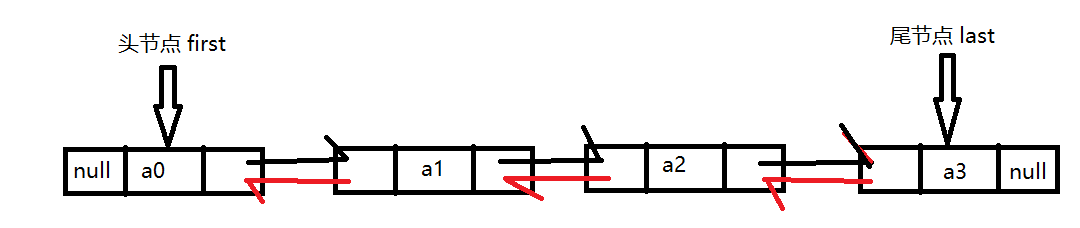
插入 / 删除

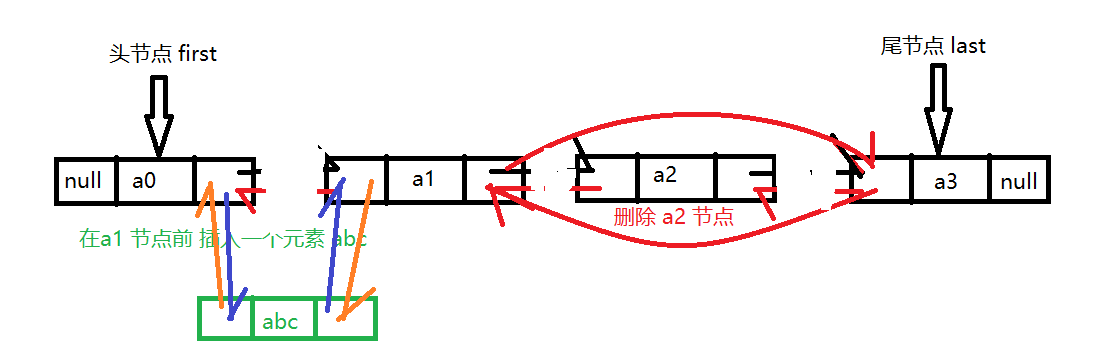
1.4.4 双向链表实现线性表

package com.yuanwu.ei.dao.Impl;

import com.yuanwu.ei.dao.MyList;

public class MyDualLinkedList implements MyList{
	private Node first; // 指向头节点 
	private Node last;	// 指向尾节点 
	private int size ;
	
	// 返回元素的个数 
	@Override
	public int getSize() {
		return size;
	}

	// 判断 线性表是否为空 
	@Override
	public boolean isEmpty() {
		return size == 0;
	}

	// 在指定的索引值 插入元素
	@Override
	public void insert(int i, Object e) {
		// 检索索引值是否越界
		if (i < 0 || i > size) {
			throw new  IndexOutOfBoundsException(i + "下标越界");
		}	
		// 2、如果 i==0 ，z在头部添加元素
		if (i == 0) {
			addFirst(e);
		} else if (i== size) {
			// 3、 如果 i==size，在尾部添加元素
			addlast(e);
		} else {
			// 4、找到 i 节点 ，在i节点的前面插入元素
			Node pNode = getNode(i);
			Node prevNode = pNode.prev;
			// 生成新的节点 
			Node newNode = new Node(e, prevNode, pNode);
			// 修改 后继节点 
			prevNode.next = newNode;
			// 修改 前驱节点 
			pNode.prev = newNode;
			// 节点个数 +1 
			size++;
		}
	}

	// 返回索引值对应的节点
	public Node getNode(int i) {
		Node pNode = first;	// 赋值？ pNode 指向 头节点 
		/*
		 * 假设 i=4   x 循环 0 1 2 3  x<4
		 * 第一次循环 pNode = pNode.next	头节点的下一个节点的引用 
		 * 1、比如 	头节点的下一个节点的引用是1 ，
		 * 2、但现在有一个插入进来 ，就表示  pNode的下一个节点的引用 指向 1 ，
		 * 3、pNode 节点 在 1节点的前面了，实现 插入节点
		 * 第二次循环 pNode = pNode.next.next
		 * 第三次循环 pNode = pNode.next.next.next
		 * .......
		 * */
		for (int x = 0; x < i; x++) {
			pNode = pNode.next;	// 指向 ？	pNode  指向 第 i 个节点  【的下一个节点引用】
		}
		return pNode;
	}

	private void addlast(Object e) {
		// 保存原来的尾节点 ，【指向尾节点】
		Node pNode = last;
		// 生成一个新的节点
		Node newNode = new Node(e,last,null);
		if (pNode == null) {
			first = newNode;
		} else {
			pNode.next = newNode ;
		}
		// 尾节点 指针后移 
		last = newNode;
		size++;
	}

	public void addFirst(Object e) {
		// 保存原来的头节点 
		Node pNode = first;
		// 创建一个新节点 
		Node newNode = new Node(e,null,first);
		// 原来的头节点 指向新节点	，头节点 ，指针前移 
		first = newNode;
		// 判断 原来的头节点 == null  为空
		// 如果空 ，尾节点 指向新节点
		if (pNode == null) {
			last = newNode;
		} else {
			// 不为空 ，原来的头节点 的前驱节点(上一个节点的引用), 指向 新的节点 
			pNode.prev = newNode;
		}
		// 节点个数 +1
		size++;
	}

	// 判断 链表中 是否包含指定的元素e ，如果存在返回true
	@Override
	public boolean contains(Object e) {
		return indexOf(e) >= 0;
	}

	// 判断元素e 在链表中第一次出现的位置，不存在则返回 -1
	@Override
	public int indexOf(Object e) {
		int count = 0;	//保存元素e 的索引值
		// 依次遍历链表中的节点 ，比较 节点元素 与 指定e 是否一样 
		if (e == null) {	// 如果 元素 e 为空
			// for循环 	从头节点开始遍历 ，循环条件 pNode != null	，每循环一次 pNode指向下一节点的引用
			for (Node pNode = first; pNode != null; pNode = pNode.next) {
				if (pNode.data == null) {
					return count;
				} 
				count++; //	索引值+1
			} 
		} else {
			for (Node pNode = first; pNode != null; pNode = pNode.next) {
				if (e.equals(pNode.data)) {
					return count;
				}
				count++; //	索引值+1
			}
		}
		
		return -1;
	}

	// 从链表中删除指定的元素 ，并返回删除的元素
	@Override
	public Object remove(Object e) {
		// 找到元素e 的索引值
		int index = indexOf(e);
		if (index < 0) {
			return null;
		}
		return remove(index);
	}

	// 从链表中删除指定索引值的元素 ，并返回删除的元素 
	@Override
	public Object remove(int i) {
		// 是否越界
		if (i < 0 | i > size) {
			throw new IndexOutOfBoundsException(i + "下标越界");
		}
		// 找到 索引i 对应的节点 
		Node pNode = getNode(i);
		// 第 i 个 节点  ，第8个节点
		Node prevNode = pNode.prev;	// prevNode 指向 第i个节点的前驱节点	8的前驱节点 是 7	prevNode 指向 7的后继节点
		Node nextNode = pNode.next;	// nextNode 指向 第i个节点的后继节点	8的后继节点 是 9	nextNode 指向 9的前驱节点 
		
		// 删除头节点 	
		if (prevNode == null) {
			// 
			// 头节点 指向 第 i 个节点的下一个节点引用 
			first = nextNode;
		} else {
			// i-1节点的下一个节点引用 指向 i+1节点 
			// i-1节点的后继节点 指向 i+1节点的前驱节点 
			prevNode.next = nextNode;
		}
		// 删除尾节点 
		if (nextNode == null) {
			// 尾节点 指向 i-1 节点 
			last = prevNode;
		} else {
			// i+1节点的上一个节点引用 指向 i+1 节点
			// i+1节点的前驱节点 指向 i-1节点的 后继节点 .
			nextNode.prev = prevNode;
		}
		// 元素个数 -1
		size--;
		return pNode.data;
	}

	// 替换
	@Override
	public Object replace(int i, Object e) {
		// 检索是否越界
		checkIndexBounds(i);
		// 找到索引值 i 的节点 
		Node pNode = getNode(i);
		// 保存替换之前的data
		Object oldData = pNode.data;
		pNode.data = e;
		return oldData;
	}

	// 返回指定索引的元素
	@Override
	public Object get(int i) {
		// 检索是否越界
		checkIndexBounds(i);
		// 找到 索引值为 i 的节点 
		Node pNode = getNode(i);
		return pNode.data;
	}

	// 在指定元素前面插入节点
	@Override
	public boolean insertBefore(Object pObject, Object e) {
		// 获取指定元素的索引值 
		int count = indexOf(pObject);
		if (count < 0) {	// 链表中 不存在 pObject
			return false;
		}
		insert(count, e);
		return true;
	}

	// 在指定元素后面插入节点 
	@Override
	public boolean insertAfter(Object pObject, Object e) {
		// 获取指定元素的索引值 
		int count = indexOf(pObject);
		if (count < 0) {	// 链表中 不存在 pObject
			return false;
		}
		insert(count + 1, e);
		return true;
	}
	
	public class Node{
		Object data;
		Node prev;	//指向前驱节点
		Node next;	//指向后继节点 
		public Node(Object data, Node prev, Node next) {
			super();
			this.data = data;
			this.prev = prev;
			this.next = next;
		}
	}
	@Override
	public String toString() {
		StringBuilder sBuilder = new StringBuilder();
		sBuilder.append("[");
		for (Node node = first ; node != null; node = node.next) {
			sBuilder.append(node.data);
			if (node != last) {
				sBuilder.append(",");
			}
		}
		sBuilder.append("]");
		return sBuilder.toString();
	}
	
	private void checkIndexBounds(int i) {
		if (i < 0 || i >= size) {
			throw new IndexOutOfBoundsException(i + "下标越界");
		}
	}

}

1.5 顺序存储与链式存储实现线性表的比较

1.5.1 时间上的比较

线性表的基本操作：查询、插入、删除

查询：

数组顺序存储，直接通过索引值访问每个元素，实现了数组元素的随机访问

链表链式存储，每次从头节点或者尾节点开始依次查找

如果线性表主要是用于查询操作，优先选择顺序存储的线性表

插入 / 删除

数组顺序存储实现的线性表，在插入 / 删除时，需要移动大量的元素

链表链式存储，只需要修改节点的前驱后继指针指向即可，不需要移动元素。

如果线性表经常用于插入 /删除操作，优先选择链式存储实现的线性表。

1.5.2 空间比较

顺序存储：预先分配一块连续的存储空间，在使用过程中会出现闲置的空间

链式存储：存储空间是动态的，不会浪费空间

如果线性表的长度经常变化，优先选择链式存储

如果线性表的长度变化不大时，优先选择顺序存储。因为链式存储需要分配额外的空间存储节点的前驱和后继。

2 栈与队列

栈与队列，从逻辑结构上看，也是线性结构，是操作受限的线性结构

2.1 栈

2.1.1 栈的特点及抽象数据类型

栈 (Stack) ，也称为堆栈，是一种操作受限的线性表，栈只允许线性表的一端进行插入 / 删除等操作，不允许在其他位置插入 / 删除。

在线性表中进行插入 / 删除的一端称为栈顶 (top) ，栈顶保存的元素称为栈顶元素，相对的另一端称为栈底（button）

如果栈中没有数据元素称为空栈。

向栈中插入元素，称为进站或入栈，从栈中删除元素称为退栈或出栈，

栈的插入 / 删除操作只允许在栈顶进行，后进炸的元素必定先出栈，称为 “ 先进后出” 表

（First In last Out ，简称 FILO ，先进后出），

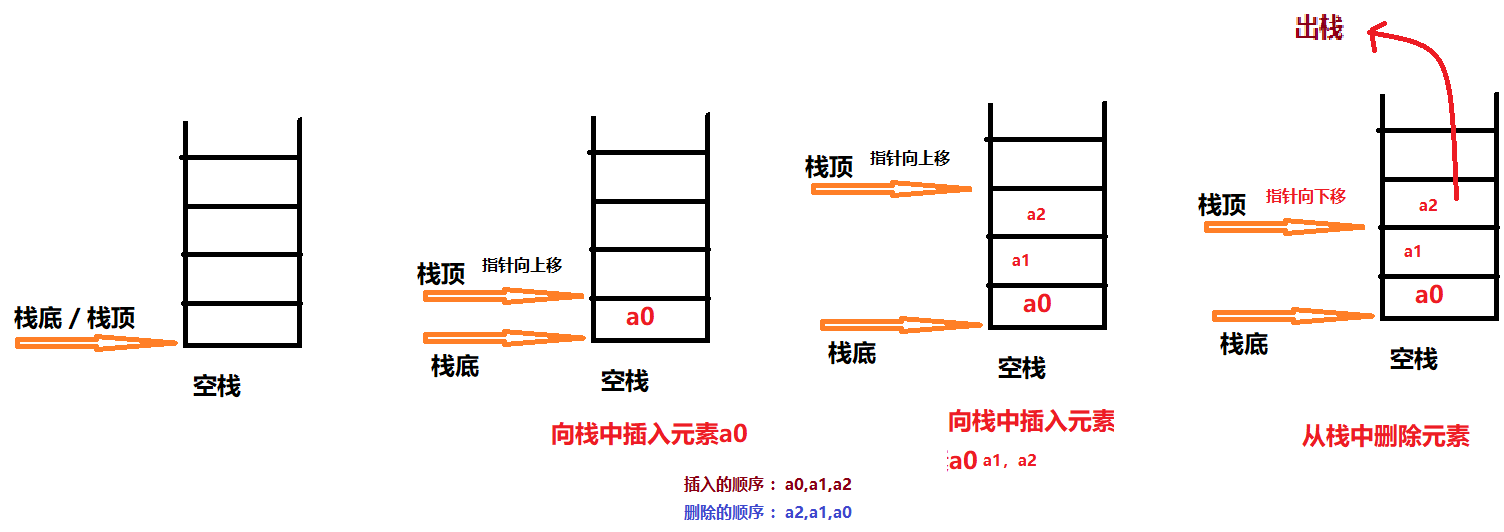
堆栈抽象数据类型的定义：

ADT Stack {

数据对象：D={a0,a1,a2...an, ai 是同一种数据类型的元素}

数据关系：R={<ai,ai+1>}

基本操作：

getSize() 返回元素的个数

isEmpty() 判断堆栈是否为空

push(Object) 压栈，入栈

pop() 弹栈，出栈

peek() 返回栈顶元素

}ADT Stack

2.1.2 栈的顺序实现

接口：

public interface MyStack {

	// 返回元素个数
	int getSize();
	// 判断 栈是否为空
	boolean isEmpty();
	// 压栈
	void push(Object e) ;
	// 弹栈
	Object pop();
	// 返回栈顶元素 
	Object peek();
	
}

实现：

public class MyArrayStack implements MyStack{
	private Object[] elements;
	// 堆栈 初始化容量
	private static final int DEFAULT_CAPACITY = 16;
	// 定义一个栈顶指针 
	private int top ;
	
	// 默认初始化 
	public MyArrayStack() {
		elements = new Object[DEFAULT_CAPACITY];
	}
	
	// 指定容量初始化 
	public MyArrayStack(int initialCapacity) {
		elements = new Object[initialCapacity];
	}
	
	// 返回元素个数 
	@Override
	public int getSize() {
		return top;
	}

	// 判断栈是否为空 
	@Override
	public boolean isEmpty() {
		return top <= 0;
	}

	// 压栈 
	@Override
	public void push(Object e) {
		// 判断堆栈是否已满 ，数组扩容 
		if (top >= elements.length) {
			// 定义一个更大的数组
			Object[] newData = new Object[elements.length * 2];
			// 把原来的数组内容复制到大的数组中
			for (int i = 0; i< top; i++) {
				newData[i] = elements[i];
			}
			// 让原来的数组名指向新的数组 
			elements = newData;
		}
		// 把元素存储到栈顶指针指向的位置
		elements[top] = e;
		// 栈顶指针上移
		top++;
	}

	// 弹栈 
	@Override
	public Object pop() {
		// 判断堆栈是否已空 
		if (top <= 0) {
			throw new StackOverflowError("栈已空 ");
		}
		top--;	// 栈顶指针向下移 
		return elements[top];
	}

	// 返回栈顶元素 
	@Override
	public Object peek() {
		return elements[top];
	}
	
	// 重写 toString
	@Override
	public String toString() {
		StringBuilder sBuilder = new StringBuilder();
		sBuilder.append("[");
		for (int i = top-1; i >= 0; i--) {
			sBuilder.append(elements[i]);
			if (i > 0) {
				sBuilder.append(",");
			}
		}
		sBuilder.append("]");
		return sBuilder.toString();
	}

}

2.1.3 栈的链式实现

使用链表作为栈的存储结构，也称为链栈

实现：

public class MyLinkStack implements MyStack{
	private Node top;	// 存储栈顶的引用 
	private int size;	// 保存栈堆元素的个数
	
	// 返回堆栈元素的个数
	@Override
	public int getSize() {
		return size;
	}

	// 判断堆栈是否为空 
	@Override
	public boolean isEmpty() {
		return size == 0;
	}

	// 压栈 
	@Override
	public void push(Object e) {
		// 根据 元素生成节点 ，插入到 链表的头部
		Node pNode = new Node(e, top);
		// 修改栈顶元素指向新的节点 
		top = pNode;
		size++;	//栈顶元素个数+1
	}

	// 弹栈 
	@Override
	public Object pop() {
		if (size < 1) {
			throw new StackOverflowError("栈已空");
		}
		Object  OldNode = top.data;	// 保存 原来的栈顶元素 
		// 栈顶指针 指向 栈顶元素的下一个节点引用 
		// 比如  1 2 3 ，删除1，top的下一个节点引用 就是 2 ，栈顶指针 指向 2 
		top = top.next;		// 指针下移 
		size--;
		return OldNode;
	}

	// 返回栈顶元素 
	@Override
	public Object peek() {
		// 判断 栈是否为空 
		if (size < 1) {
			throw new StackOverflowError("栈已空");
		}
		return top.data;
	}
	
	public class Node{
		private Object data;
		private Node next;
		public Node(Object data, Node next) {
			super();
			this.data = data;
			this.next = next;
		}
	}
	
	@Override
	public String toString() {
		StringBuilder sBuilder = new StringBuilder();
		sBuilder.append("[");
		/*
		 * top 赋值给 pNode 指向 栈顶 ，循环条件 pNode 不为空 ，pNode 指向 栈顶的下一个节点指向  pNode 所代表的就是当前栈元素 
		 * */
		for (Node pNode = top; pNode != null; pNode = pNode.next) {
			sBuilder.append(pNode.data);
			if (pNode.next != null) {
				sBuilder.append(",");
			}
		}
		sBuilder.append("]");
		return sBuilder.toString();
	}
	
}

2.1.4 栈的应用

栈的特点：先进后出

1 、进制转换

public class TestBaseConversion {

	public static void main(String[] args) {
		System.out.println(convert(100, 2));
	}
	
	public static String convert(int num ,int decimal) {
		/*
		 * 取余
		 * 除以二
		 * 把 取余的值 压栈 
		 * */
		MyArrayStack stack = new MyArrayStack();
		int i = 1;
		int remainder = num % decimal;	// 余数
		while(num != 0) {
//			int remainder = num % decimal;
//			num = num / decimal;
			stack.push(remainder);	//余数压栈
			num = num / decimal;
			remainder = num % decimal;
		}
		
		// 出栈 ，余数倒叙
		StringBuilder sBuilder = new StringBuilder();
		while(!stack.isEmpty()) {
			sBuilder.append(stack.pop());
		}
		return sBuilder.toString();
	}

}

2 、检测表达式中括弧是否匹配

假设表达式中包含三种括弧：小括弧() 、中括弧[] 、大括弧 {} 。这三种括弧可以任意嵌套。

(3+5) * [3-6] - {23/4} + ([{}])

对于任意一个左括弧都需要有一个相应的有括弧匹配。

最早出现的右括弧应该与最早出现的左括弧匹配，【符合栈的特点】

算法：

读取整个表达式，如果是左括弧就直接入栈，等待与它对应的右括弧出现；

如果是右括弧，则与当前栈顶的左括弧判断是否匹配，

如果不匹配，说明表达式不合法。

如果是右括弧，栈已空，表示不合法。

读取完整个表达式，栈堆不空，表示右左括弧没匹配上，表达式不合法；

读完整个表达式，栈是空的表示所有的括弧都能匹配上。

实现：

public class TestBracketMatch {

	public static void main(String[] args) {
		String e ="({[]})";
		boolean a = bracketMatch(e);
		System.out.println(a);		// true
	}
	
	// 检测expression表达式 中的括弧是否匹配 
	public static boolean bracketMatch(String expression) {
		MyArrayStack stack = new MyArrayStack();
		// 遍历整个表达式 ，如果是左括弧就入栈 ，如果是右括弧 ，就出栈进行判断是否匹配
		for (int i = 0; i < expression.length(); i++) {
			// 取出表达式的每个字符 
			char cc = expression.charAt(i);
			switch (cc) {
			case '(':
			case '[':
			case '{':
				stack.push(cc);	//左括弧入栈 
				break;
			case '}' :
				if (!stack.isEmpty() && stack.pop().equals('{')) {
					break;
				} else {
					return false;
				}
			case ']' :
				if (!stack.isEmpty() && stack.pop().equals('[')) {
					break;
				} else {
					return false;
				}
			case ')' :
				if (!stack.isEmpty() && stack.pop().equals('(')) {
					break;
				} else {
					return false;
				}
			}
		}
		// 表达式遍历完后 ，如果栈式空的，表示括弧匹配 
		if (!stack.isEmpty()) {
			return false;
		}
		return true;
	}

}

3 、算术表达式的求值

略 ....... 栈的应用

遇到将操作数压入栈，如果操作符栈为空，把第一个遇到的操作符压入栈，继续循环

遇到操作数压入栈，如果再一次遇到操作符，并且操作符栈不为空，就将操作符栈中的操作符弹栈，

1、跟遇到的操作符进行优先级比较，如果遇到的操作符的优先级高于操作符栈操作符的优先级，将遇到的操作符压入操作符栈。

继续循环遍历。

2、如果当前运算符的优先级等于栈顶运算符的优先级, 只有一种情况, 左一半小括弧遇到右一半小括弧的情况

将左括弧出栈

3、如果上面两种情况都不满足，即遇到的操作符的优先级低于操作符栈操作符的优先级

取出两个操作数栈的数取出操作符栈栈顶的运算符，进行计算。然后将结果压栈

4、第三步计算完，没遍历完。如果操作符栈为空，遇到的操作符压入栈

5、当表达式遍历完，操作符栈不为空，说明还没计算完，取出操作符栈的运算符，进行运算。

将结果压栈。

2.2 队列

队列的特点及抽象数据类型

队列（Queue）简称为队，也是一种受限的线性表，只允许在线性表的一端进行插入，在表的另一端进行删除。

在插入数据的一端称为队尾（rear），在删除数据的一端称为队首（front）

向队列添加数据称为入队或进队，新入队的元素称为队尾元素。

在队列中删除元素称为出队或离队，

元素出队之后，它的后续元素称为新的队首元素。

队列是一种先进先出（First In First Out 简称FIFO）表

队列抽象数据类型的定义

ADT Queue{

数据对象：D={a0,a1,a2,a3 ....an ,ai 是同一种数据类型的元素}

数据关系：R = {<ai,ai+1}>

数据操作：

getSize() ：返回元素的个数

isEmpty() ：判断队列是否为空

enQueue(e) ：入队

deQueue() ：出队

peek() ：返回队首的元素

} ADT Queue

队列的顺序存储实现

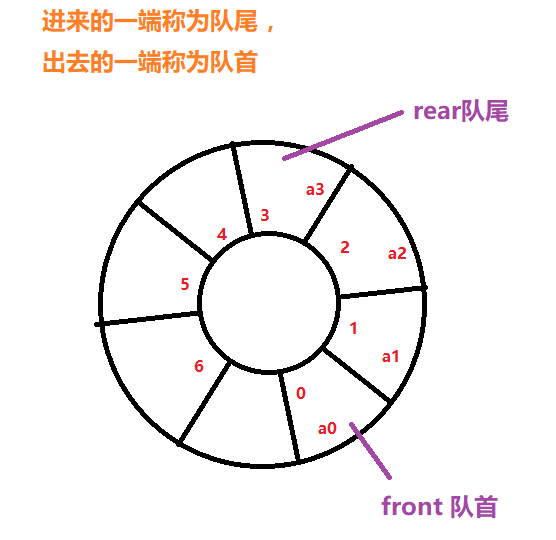
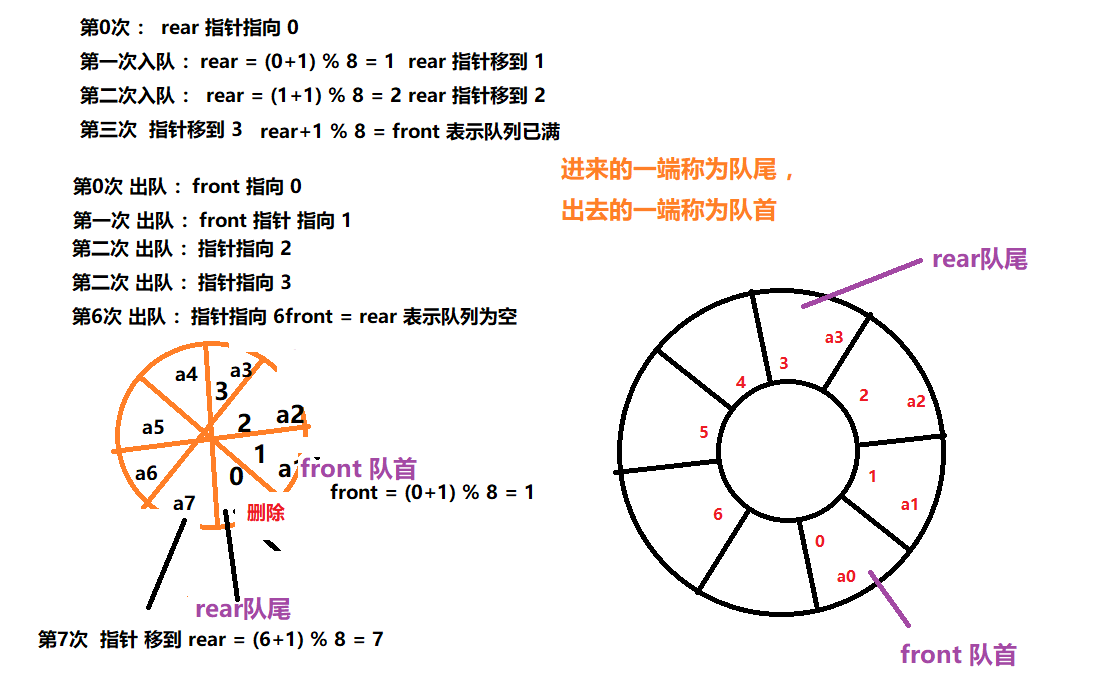
在队列的实现中，可以把数据设想为一个圆环，这种数组称为循环数组，用循环数组实现的队列称为循环队列。

用 front 指针指向队首元素所在的单元，使用 rear 指针指向队尾元素所在单元的后一个单元。

在元素入队时，将新入队的元素保存到 rear 指向的单元，然后 rear 指针后移；在出队时，将队首指针 front 指向的元返回。并且 front 指针指向后移；

如何表示队列为空？

队首元素出队，front 队首指针后移，如果 front 队首指针后移到 rear队尾指针所在的单元，即队列为空。

如何表示队列已满？

入队，rear 队尾指针指向队尾元素所在单元的下一个单元；即入队，rear 指针后移。如果 rear指针后移到 front 队首指针所在单元，即队列已满

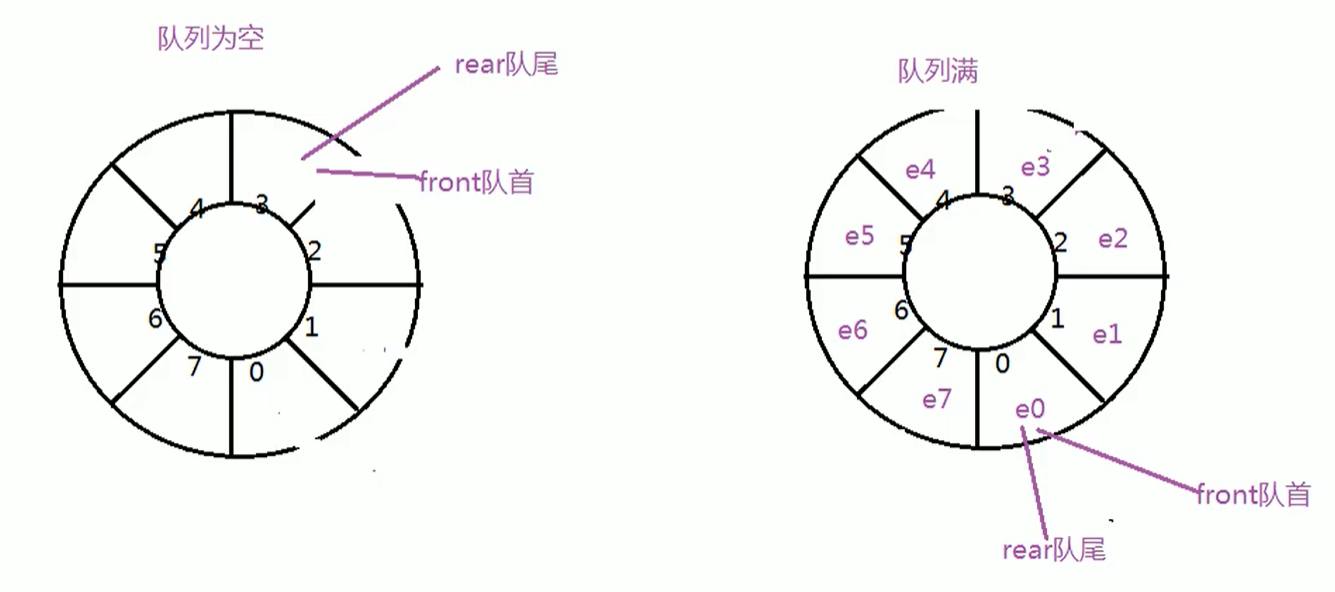
**一般情况下，采用下两种fang'shi表示队列已满 **

1）、少用一个存储单元，当队尾指针 rear 的下一个单元是队首指针 front 时，停止入队；

即 (rear + 1) % capacity == front 时表示队列满，队尾指针所在单元 +1 对容量取余 == fornt

当 front == rear 时表示队列已空。

2）、增设一个标志表示队列为空还是已满，通常用 size 变量表示元素的个数，当 sizze == 0时队列已空当 size == capacity 时队列已满。

实现：

/**
 * 队列的顺序存储实现
 * */
public class MyArrayQueue {

	private Object[] elements;	// 定义一个数组
	private static final int DEFAULT_CAPACITY = 8;	//定义数组容量初始大小
	private int front ;	// 队首 ==在删除数据的一端称为队首（front）==
	private int rear ;	// 队尾 ==在插入数据的一端称为队尾（rear）==
	private int size ;	// 保存元素个数
	
	public MyArrayQueue() {
		super();
		elements = new Object[DEFAULT_CAPACITY];
	}
	public MyArrayQueue(int initialCapacity) {
		elements = new Object[initialCapacity];
	}
	
	// 返回元素的个数 
	public int getSize() {
		return size;
	}
	
	// 判断队列是否为空 
	public boolean isEmpty() {
		return size == 0;
	}
	
	// 入队
	public void enQueue(Object e) {
		// 如果队列已满 ,可以对数组扩容
		if (size >= elements.length) {
			expandQueue();
		}
		
		elements[rear] = e;	// 把元素e存储到 rear 指针指向的单元 
		/*
		 * 第一次入队的时候 ，rear指针指向 0	添加完元素 
		 * rear 指针  = rear + 1 对 数组长度取余 ，
		 * 假设 数组长度 为 8	rear = (0+1) % 8  = 1	rear = (1+1) % 8  = 2	rear = (2+1) % 8  = 3
		 * */
		rear = (rear+1) % elements.length;	// 取余 rear 指针后移 
		size++;
	}
	
	// 队列数组扩容
	private void expandQueue() {
		// 定义一个更大的数组
		Object[] newData = new Object[DEFAULT_CAPACITY * 2];
		// 把原来的数组内容复制到新的数组中
		for (int i = 0; i< size; i++) {
            /*
			 * 删除的一端 是队头  front  
			 * 所以 先复制到 新数组中 
			 * 然后 front 指针后移 ，第一次对头 指针是0，第二次 是 1 第三次 是 2
			 * 假设 初始化的时候 ，队首和队头 都处在 0这个位置 ，
			 * 队列可以看作是一个线性表的 环形数据结构 
			 * 插入数据的时候 (队尾rear)，会随着 数组长度变化而变化 ，插入数据 ，rear指针 在当前单元的基础上 +1 移动 ，
			 * 删除数据的时候(队首front)，会随着数组长度变化而变化 ，删除数据 ，front 指针指向第二个插入数据的单元 ， 从0索引值 向 数组长度的索引值变化 
			 * */
			newData[i] = elements[front];	
			front = (front + 1) % elements.length;
		}
		// 让原来的数组变量指向新的数组
		elements = newData;
		// 调整新的队首与队尾 指针 
		front = 0;
		rear = size;
	}
	// 出队 
	public Object deQueue() {
		// 如果队列为空
		if (size <= 0) {
			//抛出队列为空异常
			throw new QueueEmptyException("队列为空");
		}
		// 队列不为空 ,把front指向的元素返回 ,front指针后移 
		Object old = elements[front];	// 保存出队的元素
		/*
		 	假设队列中已经入队5个元素 ，此时要出队 
		 	即 front = (5+1) % 8 = 6
		 * */
		front = (front + 1) % elements.length;	// front指针后移
		size--;
		return old;
	}
	
	// 返回队首元素
	public Object peek() {
		// 队列为空 抛出异常
		if (size <= 0) {
			throw new QueueEmptyException("队列为空");
		}
		return elements[front];
	}
}

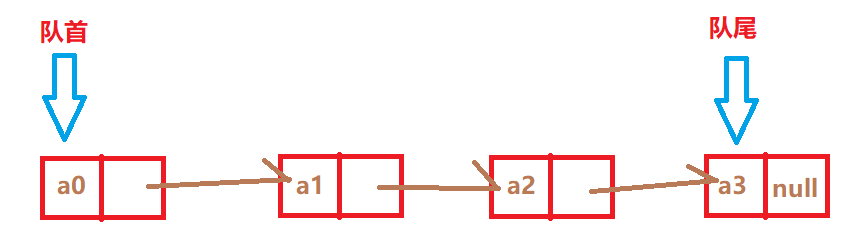
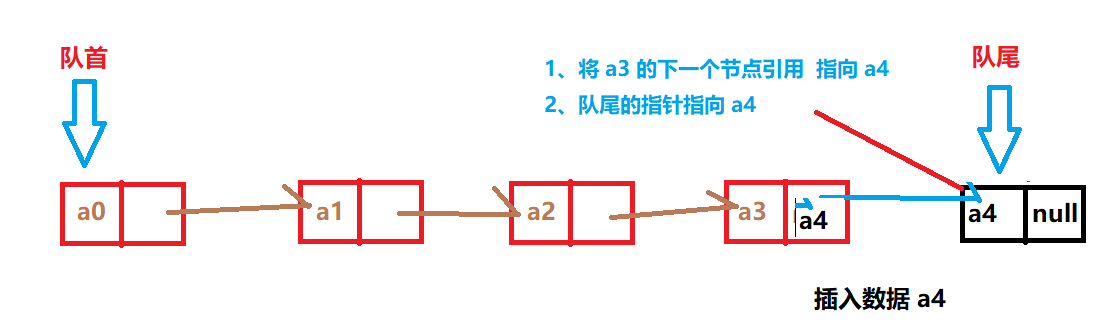
队列的链式存储实现

使用单向链表来实现队列

把链表的头部作为队首，把链表的尾部作为队尾

每次插入 / 删除元素，队首 / 队尾指针都要重新指向

实现：

/**
 * 队列的链式存储 
 * */
public class MyLinkQueue {
	private Node front;		// 队首 ==在删除数据的一端称为队首（front）==
	private Node rear;		// 队尾 ==在插入数据的一端称为队尾（rear）==
	private int size;		// 元素的个数 
	
	// 返回元素的个数 
	public int getSize() {
		return size;
	}
	
	// 判断队列是否为空
	public boolean isEmpty() {
		return size == 0;
	}
	
	// 入队 
	public void enQueue(Object e) {
		// 根据添加的元素 生成一个节点 
		Node newNode = new Node(e,null);
		// 把节点 连接到队列中 
		if (rear == null) {
			// 队尾为空 ，说明是第一个添加的元素 ，
			// 即是头节点 ，也是尾节点 。
			rear = newNode;
			front = newNode;
		} else {
			// 把节点链接到队列的尾部 
			rear.next = newNode;	// 当前队尾的下一个节点引用 指向新节点 
			rear = newNode;	     // 队尾rear 指针指向新添加的元素 。新添加的元素就是队尾
		}
		size++;
	}
	
	// 出队 
	public Object deueue() {
		// 判断队列是否为空
		if (size < 0) {
			throw new QueueEmptyException("队列为空 ");
		}
		// 保存 出队的元素
		Object old = front.element;
		// 调整队首指针指向 指针指向 当前队首的下一个节点引用 
		front = front.next;
		// 如出队后 ，队列为空 调整尾指针 。
		if (front == null) {
			rear = null;
		}
		size--;
		return old;
	}
	
	// 返回队首元素
	public Object peek() {
		if (size <=0 ) {
			throw new QueueEmptyException("队列为空");
		}
		return front.element;
	}
	
	// 通过内部类表示单向链表的节点 
	private class Node{
		Object element;
		Node next;
		public Node(Object element, Node next) {
			super();
			this.element = element;
			this.next = next;
		}
	}
	
}

3树

3.1 树的定义

树是由一个集合及该集合上定义的一种关系构成的，集合中的元素称为树的节点，定义的关系称为父子关系。父子关系的树的节点之间建立一个层次结构。

树的递归定义：

树（Tree）是由 n(n>=0) 个节点组成的有限集，当 n = 0是，称为空树，不包含任何节点；当 n > 0是就是一颗非空树，

1、有且仅有特定的称为根的节点（root）。

2、当 n > 1时，其他节点可以分为 m ( m > 0) 个互不相交的有限集 T1,T2, .... , 其中每个有限集本身又是一棵树，称为根节点的子树（SubTree）

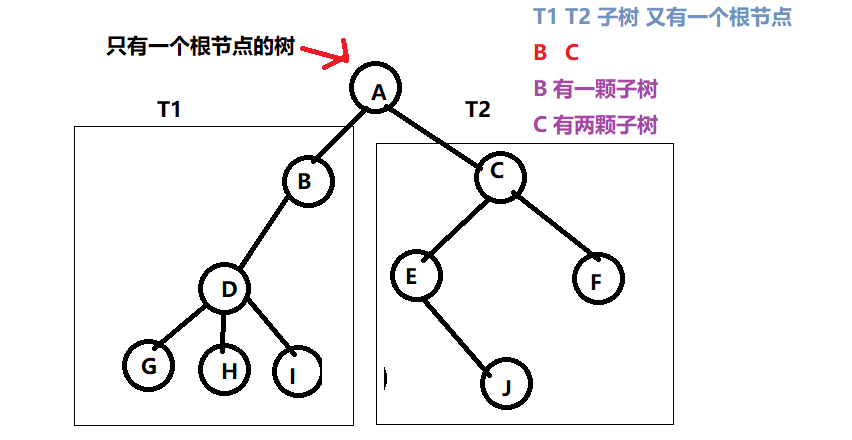
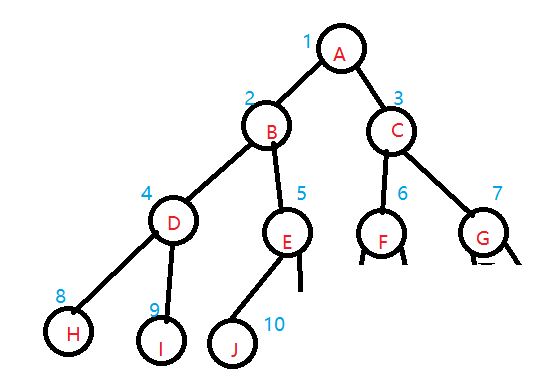
在上图中，节点A 时根节点，它包含 T1和 T2两颗子树，T1={BDGHI} ,T2={CEFJ}，每课子树又是一棵树，在T1子树中，B是根节点，在 T2 子树中，C 是根节点

注意：

当 n > 0 时，在非空树中，根节点是唯一的

当 m > 0 时，某个节点的子树时没有限制的，并且各个子树肯定是不相交的

3.2 相关概念

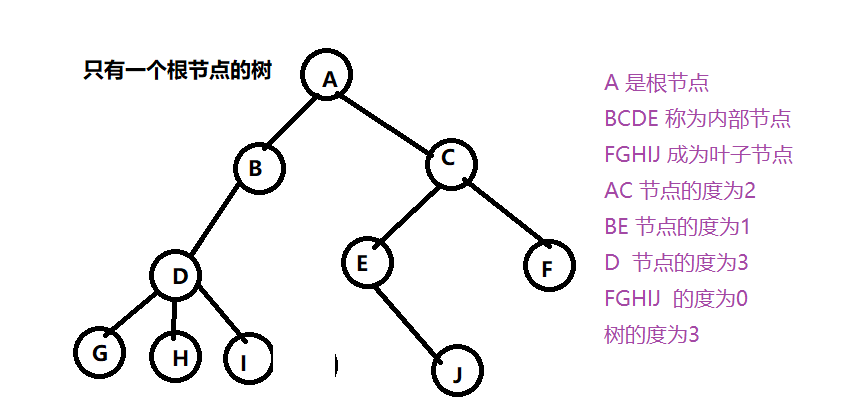
节点拥有的子树的数量称为节点的度（Degree）

度为 0 的节点称为叶子节点（Leaf）或者终端节点，度不为 0 的节点称为分支节点或非终端节点。

除了根节点外，分支节点也称为内部节点。

树的度是树内各个节点中度的最大值。

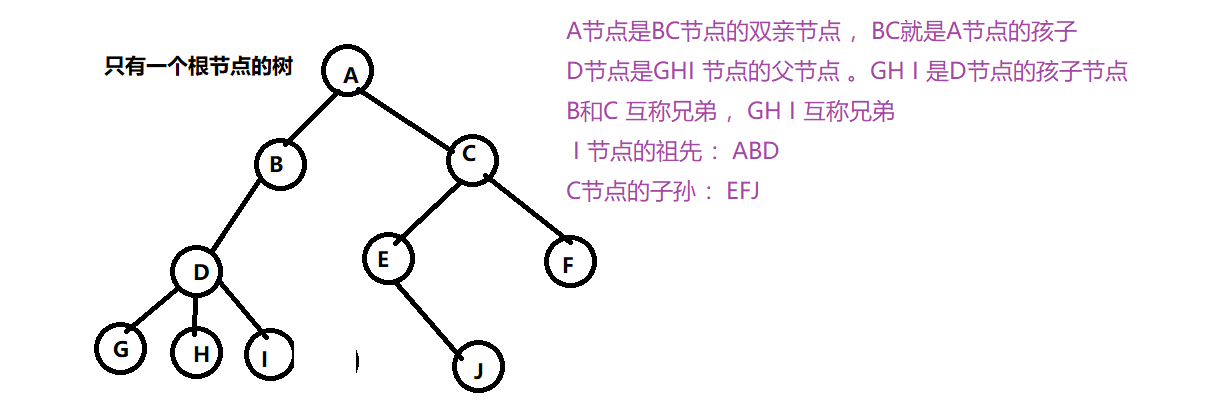
节点的子树的根称为该节点的孩子（Child），相应的该节点称为孩子节点的双亲（Parent）节点或父节点；

例如：BC 是 A 的子树，BC 是 A 是孩子节点，A 是 BC 的双亲节点

父子节点之间的连线是树的一条边，树中节点数等于数的边数 + 1

在树中，根节点没有双亲节点，其他节点都有并且只有一个父节点。每个节点可以有多个孩子节点。

同一个双亲的孩子节点之间互称为兄弟（Sibling）

节点的祖先是从根节点到该节点所经过的分支上的所有节点

以某节点为根的子树上的任一节点都称为该节点的子孙。

节点的层次（Level）是从根节点开始的，根为第一层，根的孩子为第二层，依次类推，注意：有些人把层次的定义是从0开始的，即根为第0 层

如果某节点在第 i 层，则其子树的根就在 i+1 层

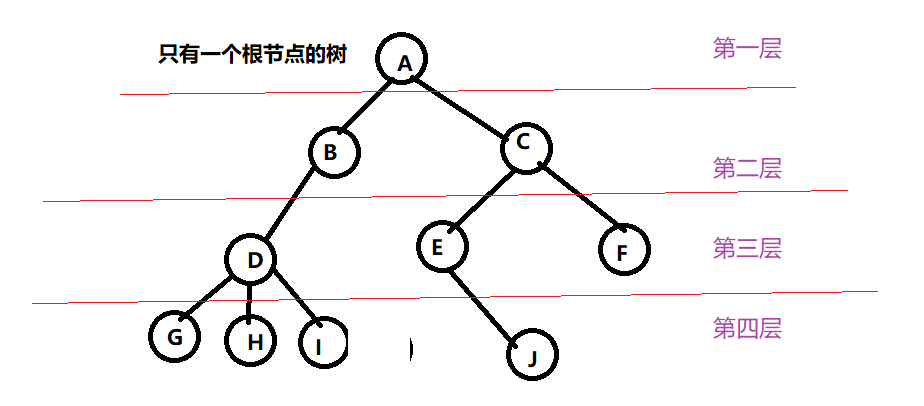
双亲节点（父节点）在同一层次上的节点互为堂兄弟，例：DEF 互为堂兄弟

树中节点的最大层次称为树的深度（Depth）或高度，当前树的高度是 4 ，

在树中 k+1 个节点通过 k 条边构成的序列称为长度，为 k 的路径。如上图中：

{(D,B),(B,A),(A,C),(A,E)} 构成一条连接 D 节点与 E 节点的路径。该路径的长度为 4 ；在树中任意两个节点都有唯一的路径。从根节点开始，存在到其他任意节点的唯一路径。

如果将书的节点的各个子树看作是从左到右的顺序。不能互换的，则称该树为有序树。否则称为无序树，如果不特殊说明，一般讨论的是有序树。

树中所有节点最大读书为 m 的有序树称为 m 叉树；例：D节点的度为 3 。则将该有序树称为三叉树。

森林（Forest）是 m （m >= 0）颗互不相交的树的集合。对树的每个节点而言，其子树的集合就是森林，删去树的根就得到一个森林。反之，把森林加上一个树的根就变成一棵树。

3.3 树的抽象数据类型

ADT Tree{

数据对象 D ：D是具有相同性质的数据元素的集合。

数据对象 R ：如果 D 是空则 R 为空；如果 D 不为空，D 中存在唯一一个称为根的元素 root ；该元素没有前驱，除了根元素外， D 中每个元素有且仅有一个前驱；

数据操作：

getSize() ：返回元素的个数

getRoot() ：返回树的根元素

getParent(x) ：返回 x 节点的父节点

getFirstChild(x) ：返回 x 节点的第一个孩子节点

getNextSibling(x) ：返回 x 节点的下一个兄弟节点，如果 x 是最后还记节点，返回null

getHeight(x) ：返回以 x 节点为根的树的高度。

insertChild(x,child) ：将节点 child 为根的子树插入到当前树中，作为 x 节点的孩子节点

deleteChild(x,i) ：删除节点 x 的第 i 颗子树

preOrder(x) ：先序遍历 x 为根的树

inOrder(x) ：中序遍历 x 为根的树

postOrder(x) ：后序遍历 x 为根的树

levelOrder(x) ：按层次遍历 x 为根的树

} ADT Tree

3.4 树的存储结构

1、双亲表示法

树中的节点，除了根节点外，都有且仅有一个双亲结点，可以在使用数组存储树中的每个节点。数组的下标就是数组的位置指针，每个节点再增加一个指向双亲的指针域，

节点的结构可以定义为：

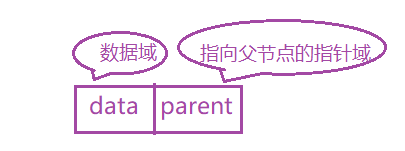
使用该方式

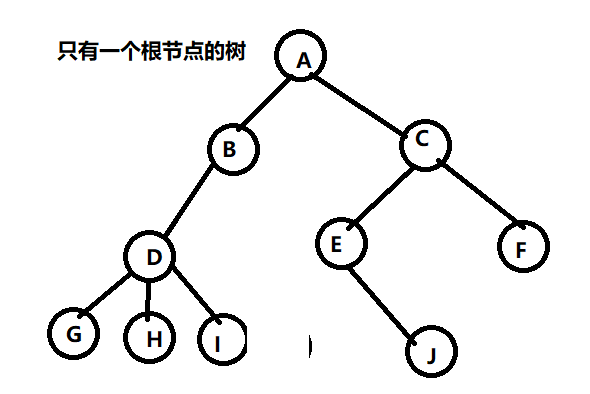
存储结构为：

数组下标	data	parent 父节点的存储下标	firstChild(长子域)
0	A	-1	1
1	B	0	3
2	C	0	4
3	D	1	6
4	E	2	9
5	F	2	-1
6	G	3	-1
7	H	3	-1
8	I	3	-1
9	J	4	-1

在双亲表示法存储结构中，可以方便的通过 parent 指针域找到该节点的父节点，如果要找到某个节点的孩子节点，需要遍历整个数组。

可以在节点中再增加一个长子域，指向第一个孩子的指针域。如果没有长子域，那么该长子域设置为 -1

#### **2、孩子表示法**

树中每个节点可能有多颗子树，可以考虑使用多重链表，每个节点可以有多个指针域，每个指针域指向它的子树的根节点。把这种方式称为多重链表表示法。

树的每个节点的度可能不一样，即每个节点的孩子节点个数不相等。一般设计以下两种方案：

方案一：

节点中指针域的个数就是数的度（树中节点最多的孩子树）

data	child1	child2	child3	childn…

节点中孩子节点域的个数就是树的度

该树使用孩子表示法，可以表示为：

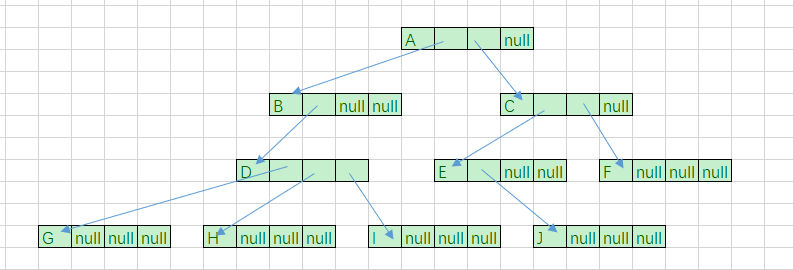
如果树种各个节点的度相差很大时，很浪费空间，有很多节点的指针域是空的，这种表示方法适合树的各个节点度相差很小的情况。

第二种方案：每个节点的指针域的个数等于该节点的度，再节点中专门定义一个存储该节点度的域：

如节点可以设计为：

data	Degree (度)	child1	child2	child3	childn…

上图的树还可以表示为：

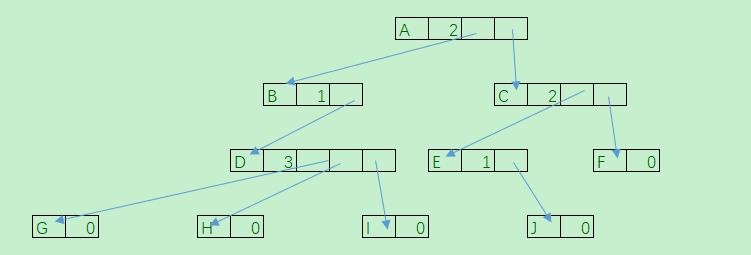
这种方法提高了空间的利用率，但是各个节点的结构不一样，还要维护节点的度的值，会增加时间上的损耗。

可以定义一个线性表存储树中的所有节点的信息，称为节点表。每个节点建立一个孩子表，孩子表只存储孩子节点在数组中的存储位置。由于每个节点的孩子节点的个数是不确定的，经常使用一个链表表示孩子之间的关系，这就是孩子表示法。

如上树(第二种方案)使用孩子表示法，可以表示为：(节点表包括下标、数据) (孩子表包括firstchild)

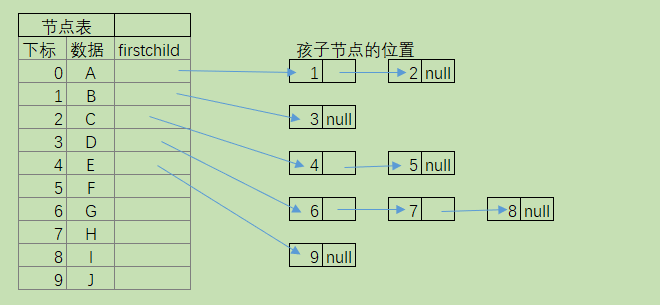
在上图这种表示法中，需要设计两种节点，一个节点数组中表头节点，包括数据域和指向第一个孩子节点的指针域。

如：

还需要设计一个孩子节点，存储孩子节点在数组的下标，和指向下个孩子节点的指针。如下图：

(指向当前孩子节点的兄弟节点。)

在这种结构中，可以方便查找某个节点的孩子节点，也可以方便查找某个节点的兄弟节点，只需要访问这个节点的孩子链表即可，如果需要查找节点的父节点，还需要遍历整棵树：我们可以在节点表中，即数组中的节点增加一个指向父节点的指针，如：

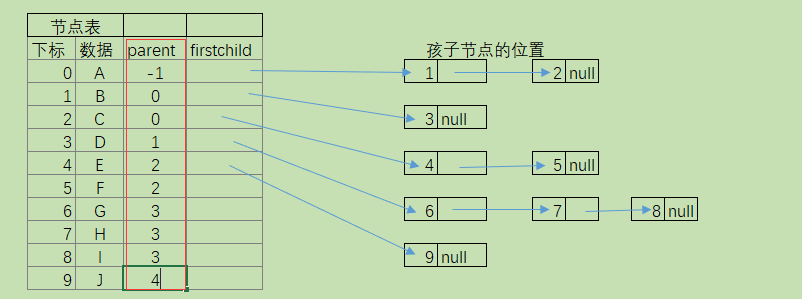
这种表示法称为双亲孩子表示法。

3、孩子兄弟表示法

从树节点的兄弟的角度来确定树的存储结构。

对于任意一棵树，它的节点的第一个孩子如果存在肯定是唯一的，如果节点的右兄弟存在也肯定是唯一的。可以设置两个指针分别指向某个节点的第一个孩子和它的右兄弟。如：

（数据域，第一个孩子节点，右兄弟节点）

使用孩子兄弟法表示树的存储结构为：

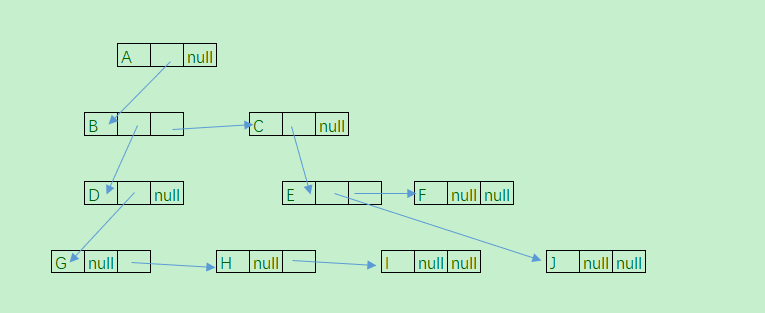
这种表示法，可以方便查找某个节点的孩子节点和右兄弟节点。

这种表示法，把一颗复杂的树转换为一颗二叉树。

3.5 二叉树

3.5.1 二叉树的特点

二叉树（Binary Tree）是由 n 个节点组成的集合，该集合要么是空集合，要么是一个由根节点和两颗互不相交的二叉树组成。

二叉树的特点：

1）、每个节点最多有两颗子树，

2）、左子树与右子树是有顺序的，从左到右

3）、即使树中的某个节点只有一个子树，那么也是区分左子树与右子树的。

二叉树的五种基本形态：

1、空二叉树

2、只有一个节点的二叉树

3、根节点只有左子树

4、根节点只有右子树

5、跟节点既有左子树又有右子树

3.5.2 特殊的二叉树

1、斜树

所有节点都只有左子树的二叉树称为左斜树。

所有节点都只有右子树的二叉树称为右斜树。

2、满二叉树

在一颗二叉树中，如果所有分支节点都有左子树和有右子树，并且所有的叶子节点都在同一层上，这样的二叉树称为满二叉树。即每层的节点都是满的。

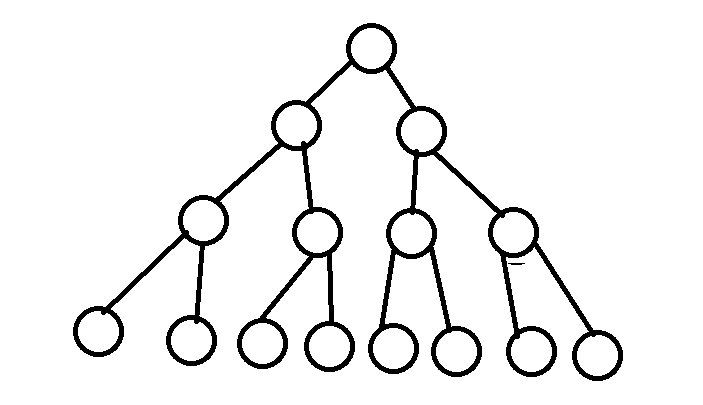
满二叉树的特点：

1）、叶子节点只能出现在最下面的一层

2）、非叶子节点的度一定是 2

3）、在同样深度的二叉树中，满二叉树的节点树是最多的，叶子也是最多的。

3）、完全二叉树

对一颗具有 n 个节点的二叉树按层次编号，如果编号为 i 的节点与同样深度的满二叉树编号为 i 的节点在二叉树中的位置完全相同，这就是一颗完全二叉树。

就是满二叉树最下层从最右侧开始去掉相邻的若干叶子节点。例：

满二叉树一定是一颗完全二叉树，但完全二叉树不一定是满的

完全二叉树的特点：

叶子节点只能出现在最下两层

最下层的叶子节点集中在左侧连续的位置

倒数第二层的叶子节点一定都在右边连续的位置。

如果节点的度为 1 ，该节点只有左孩子

同样节点数的二叉树，完全二叉树的深度最小。

3.5.3 二叉树的性质

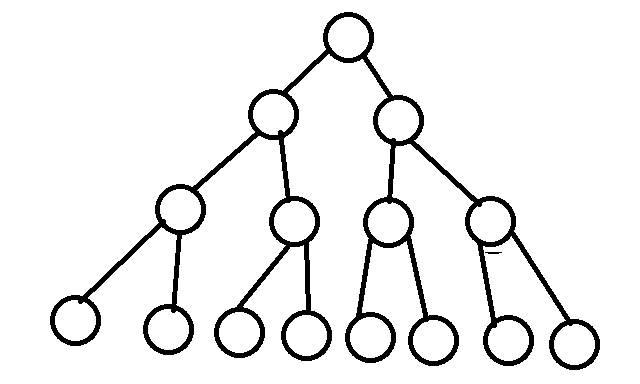
1、性质 1

在二叉树的第 i 层上最多有 2^(i-1) 个节点（i >= 1）

例：上图 >>> 第四层的节点 = 2的 i-1 次方 =2^(4-1) = 8；即第四层有八个节点。

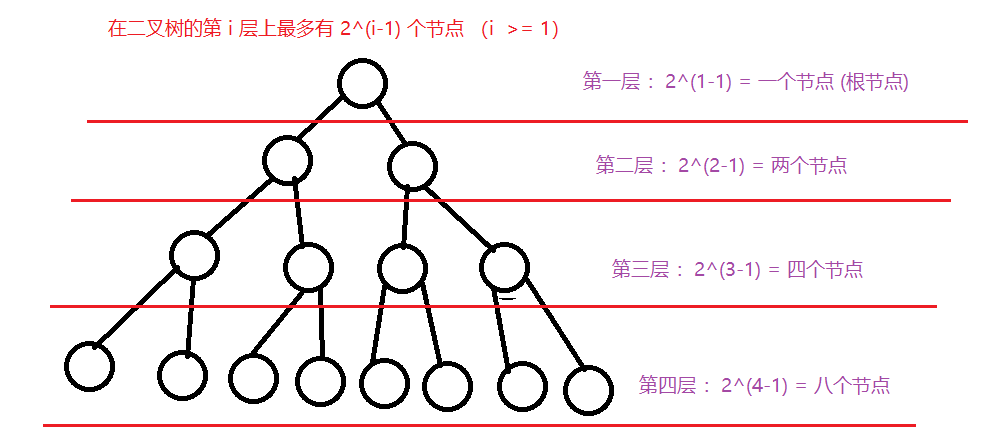
2、性质 2

深度为 k 的二叉树，最多有 2^k - 1 个节点 (二叉树总的节点)。

例：上图 >>> 如果有一层，只有一个根节点没有孩子节点，2^1 - 1 = 1 （即是根节点，也是叶子节点）

如果有四层，2^4 -1 = 15 二叉树总结点为 15 (包括根节点 )

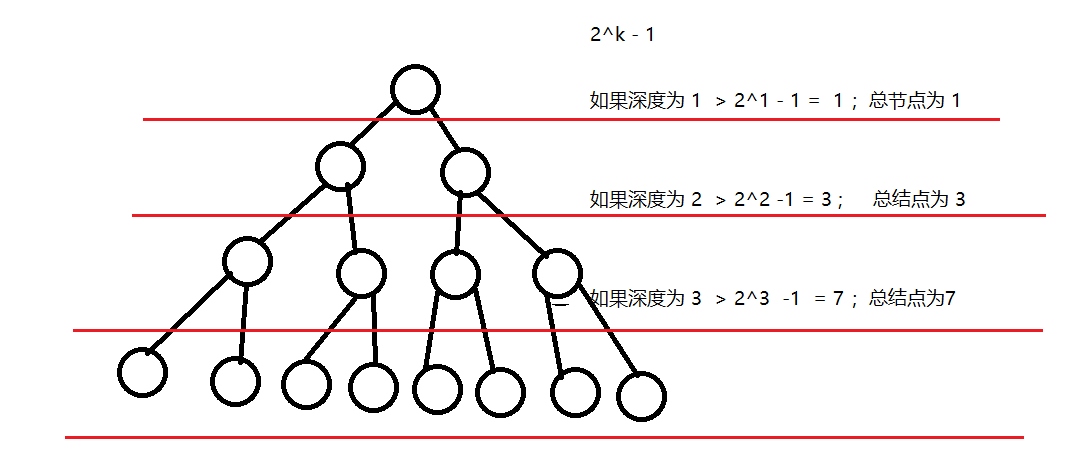
3、性质 3

对于任意一颗二叉树，叶子节点的数量 n0 ，度为 2 的节点数量 n2 ，则 n0 = n2 + 1

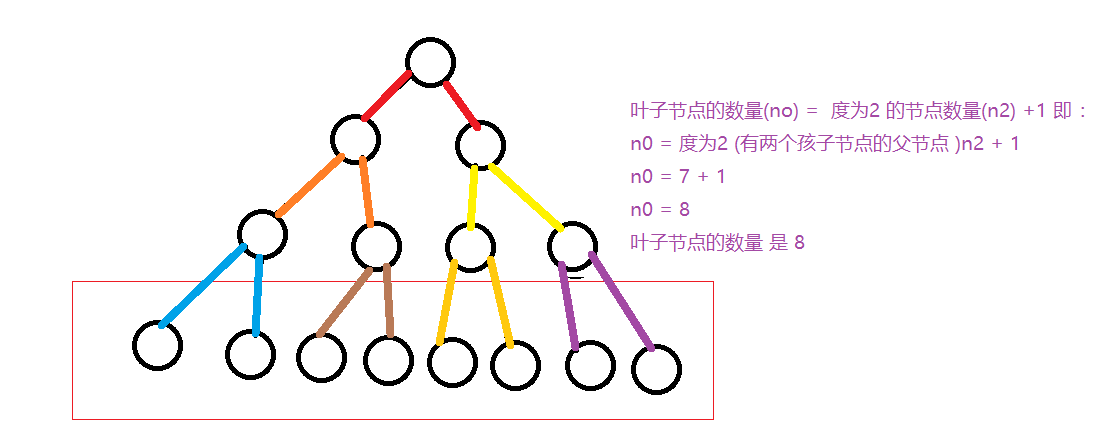
树中节点数量 = 数的边(连线) + 1

分支线的数量 = 节点总数 - 1 因为根节点没有进入的连线

n2 * 2 + n1 = n0(叶子节点) + n1(一个节点) + n2(两个节点) - 1 （根节点上面没有连线）

n2 = n0 - 1

4、性质 4

具有 n 个节点的完全二叉树深度为 floor(log2 n) + 1

满二叉树深度为 k ，节点总数量：2^k - 1 。如果把总结点的数量记为 n ，即 n = 2^k - 1 。则 k = log2(n+1)

深度为 k 的完全二叉树节点数量 n 一定小于等于同样深度的满二叉树的节点数。一定大于深度为 k-1 的满二叉树节点的数量。即：

2^k - 1 >= n > 2^(k-1) - 1 n 就是深度为 k 的完全二叉树的节点数量

n <= 2^k - 1 , 意味着 n < 2^k

2^(k-1) -1 < n , 意味着 2^(k -1) <= n

即：

2^(k-1) <= n < 2^k

对不等式的两边取对数：得到 >> k-1 <= log2 n < k

因为 k 是深度，也是一个整数， floor(log2 n) + 1

floor (xx) 是指小于等于 xx 的最大整数

5、性质 5

对一个完全二叉树进行按层次编号

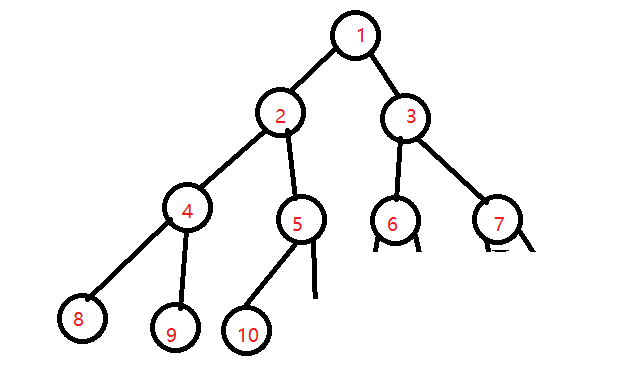
对于任意一个节点 i ，有：

如果 i==1 ，则节点 i 是二叉树的根，如果 i > 1 , 则该节点的双亲节点是 i / 2 ；

如果 2 * i > n (n 表示节点数量 ) ，则节点 i 没有左孩子，否则左孩子是 2 * i 。

如果 2 * i + 1 > n ，则节点 i 没有右孩子，否则右孩子是 2 * i + 1 .

3.5.4 二叉树的存储结构

1、二叉树的顺序存储

使用一维数组存储二叉树中的节点，节点的存储位置 (数组的下标) 可以反映节点之间的逻辑关系。

逻辑关系：

完全二叉树的顺序存储，对完全二叉树的各个节点按层次编号

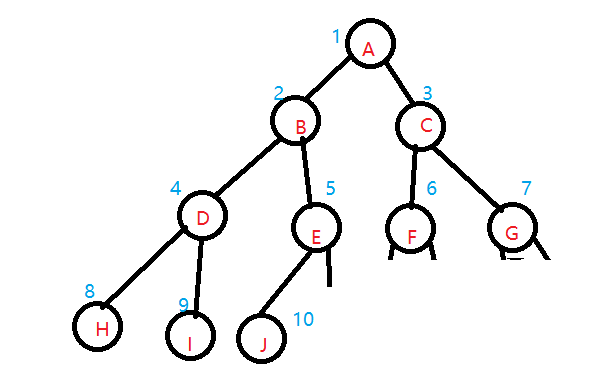
将完全二叉树存储到数组中，数组的下标对应存储位置。

如果不是完全二叉树，可以将二叉树编号，把不存在的节点设置为 null 。

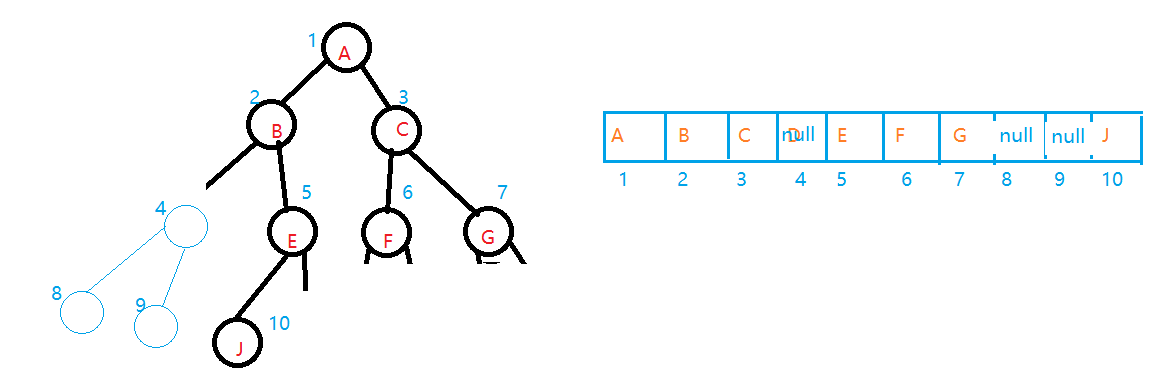
如果二叉树中有很多不存在的节点，会造成存储空间的浪费。一般情况下，顺序存储只用于完全二叉树。

**2、链式存储 **

二叉树的节点最多右两个孩子，可以为节点设计一个数据域，一个指向左孩子的指针域，和一个指向右孩子的指针域，由这样的节点组成的链表称为二叉链表。

二叉树节点的结构可以设计为：

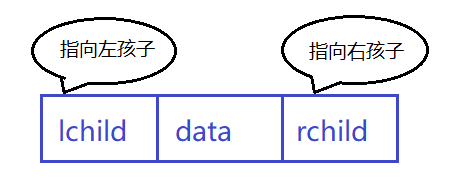
以下二叉树的二叉链表为：

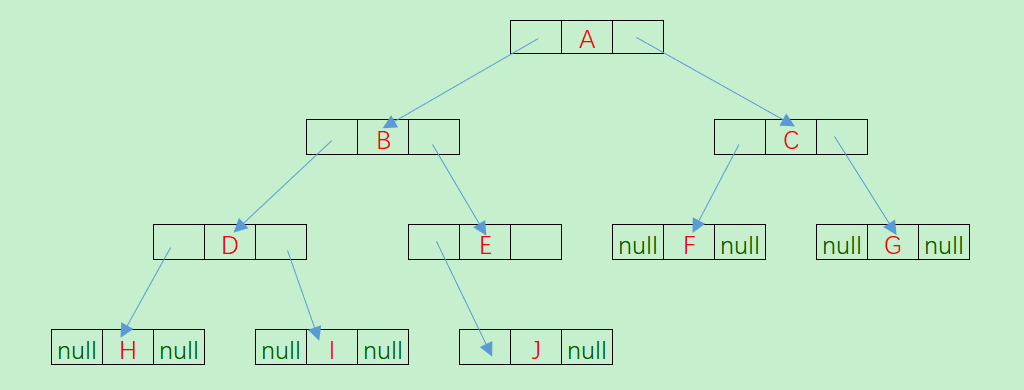
为了方便找到父节点，可以在节点上增加一个指向父节点的指针域。这种节点组成的链表称为三叉链表。

节点的结构可以设计为：

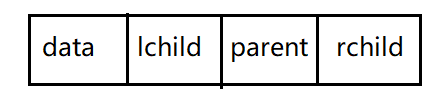
上面的二叉树使用三叉链表可以设计为：

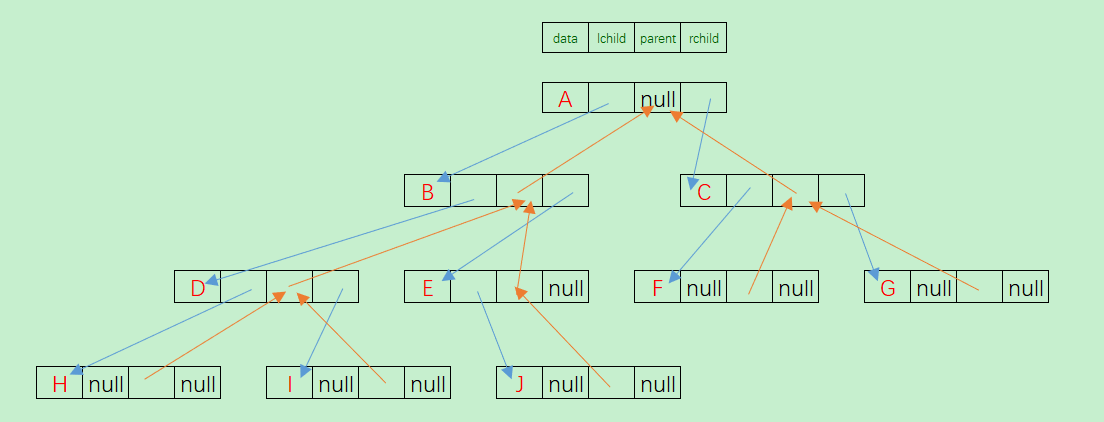
前序遍历

根节点 > 左子树 > 右子树

中序遍历

左子树 > 根节点 > 右子树

后续遍历

左子树 > 右子树 > 根节点

未完待续 .......................... ，

posted @ 2020-12-04 14:16 san只松鼠阅读(145) 评论(0) 收藏举报

刷新页面返回顶部

san只松鼠

谨本人学习数据结构算法的经历记录

数据结构

1.1 、基本概念

数据

数据元素

数据对象

数据结构

2.1、抽象数据类型

数据类型

抽象数据类型

3.1、算法及性能分析

1.3.1 算法

算法有五个特性 ：

算法设计要求

1.3.2 时间复杂度

1.3.3 算法时间复杂度分析

1.3.4 空间复杂度

1 线性表

1.1 线性表的抽象数据类型

1.2 List接口

1.3 线性表的顺序存储与实现

1.3.1 插入元素

1.3.2 删除元素

1.3.3 具体代码的实现

1.3.4 顺序存储的特点

1.4 线性表的链式存储与实现

1.4.1单向链表

1.4.2 通过单向链表实现线性表

1.4.3 双向链表

1.4.4 双向链表实现线性表

1.5 顺序存储与链式存储实现线性表的比较

1.5.1 时间上的比较

1.5.2 空间比较

2 栈与队列

2.1 栈

2.1.1 栈的特点及抽象数据类型

2.1.2 栈的顺序实现

2.1.3 栈的链式实现

2.1.4 栈的应用

2.2 队列

队列的特点及抽象数据类型

队列的顺序存储实现

队列的链式存储实现

3树

3.1 树的定义

3.2 相关概念

3.3 树的抽象数据类型

3.4 树的存储结构

1、双亲表示法

3、孩子兄弟表示法

3.5 二叉树

3.5.1 二叉树的特点

3.5.2 特殊的二叉树

3.5.3 二叉树的性质

3.5.4 二叉树的存储结构

前序遍历

中序遍历

后续遍历

未完待续 .......................... ，

公告

算法有五个特性：