AT_abc281_g [ABC281G] Farthest City题解

AT_abc281_g [ABC281G] Farthest City

看到边权为 \(1\)，想到 bfs，发现跑出来会分成一层一层的分层图，每层的数量不固定可以当作 dp 的一维。

设 \(f_{i,j}\) 为前 \(i\) 个数最后一层为 \(j\) 的方案数。

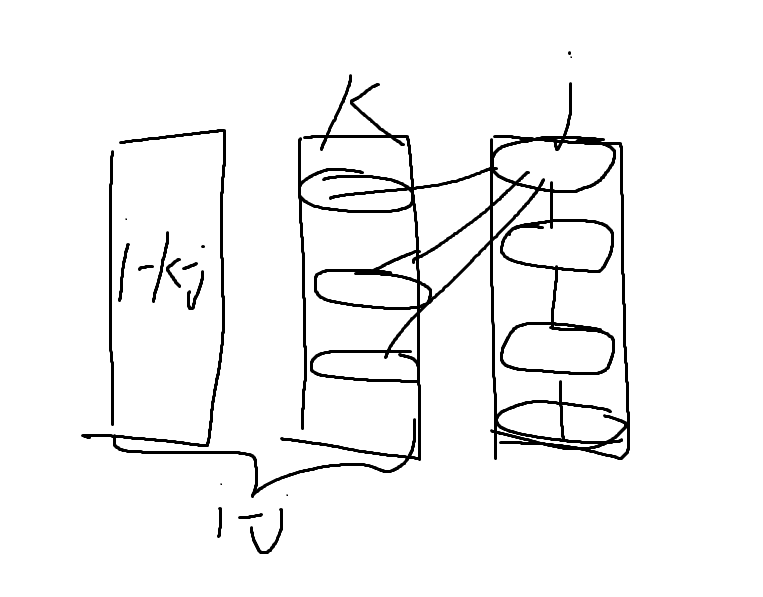
上一层为 \(k\) 个数，这层为 \(j\) 个数。

\[f_{i,j}=\sum_{i=1}^{i-j}\times 2^{C_j^2} \times (2^k-1)^{j}\times C_{n-1-{i-j}}^{j}\times f_{i-j}{k} \]

\(2^{C_j^2}\) 表示 \(j\) 层之间相互连边，\((2^k-1)^{j}\) 表示于上一层连边，至少有一条边所以-1，\(C_{n-1-{i-j}}^{j}\) 给这 \(j\) 个点编号，要从剩下中选 \(j\) 个。

#include<bits/stdc++.h>
#define ll long long
#define int ll
using namespace std;
const int N=1e6+10;
const int mod=1e9+7;

int n,m;

int c[705][705];
int f[705][705];
int pow2[N];

int quick_pow(int x,int k){
	int ans=1;
	while(k){
		if(k&1){
			ans*=x;
			ans%=m;
		}
		x*=x;
		x%=m;
		k>>=1;
	}
	return ans;
}


signed main(){
    ios::sync_with_stdio(0);
    cin.tie(nullptr);   
    cin>>n>>m;
    
    pow2[0]=1;
    for(int i=1;i<=500*500;i++){
    	pow2[i]=pow2[i-1]*2;
    	pow2[i]%=m;
	}
	c[0][1]=c[1][0]=c[0][0]=c[1][1]=1;
	for(int i=2;i<=600;i++){
		c[i][0]=c[0][i]=1;
		for(int j=1;j<=i;j++){
			c[i][j]=(c[i-1][j]+c[i-1][j-1])%m;
		}
	}
	f[1][1]=1; 
	for(int i=2;i<=n;i++){
		for(int j=1;j<i;j++){
			for(int k=1;k<=i-j;k++){
				f[i][j]+=quick_pow(pow2[k]-1,j)*pow2[c[j][2]]%m*c[n-1-(i-j)][j]%m*f[i-j][k]%m;
				f[i][j]%=m;
			}
		}
	}
    cout<<f[n][1];
    return 0;
}